AMAZON multi-meters discounts AMAZON oscilloscope discounts
1. INTRODUCTION
From the biological cell, electrical potentials are generated and it is due to the electrolytes inside and outside of the cell. A bioelectric potential may be defined as the difference in potential between the inside and the outside of a cell; there exists a difference in potential existing across the cell wall or membrane. A cell consists of an ionic conductor separated from the outside environment by a semi permeable or selectively permeable cell membrane. Human cells may vary from 1 micron to 100 microns in diameter, from 1 millimeter to 1 meter in length and have a typical membrane thickness of 100 Angstrom units. Bioelectricity is studied both from the viewpoint of the source of electrical energy within the cell and also from the viewpoint of the laws of electrolytic current flow relative to the remote ionic fields produced currents by the cell. We make measurements external to a group of cells while these cells are supplying electrolytic current flow.
1.1. Cell Potential Genesis
Experimental investigations with microelectrodes have shown that the internal resting potential within a cell is approximately - 90 mV with reference to the outside of the cell.
The equation for resting potential is e = RT F loge
where R = Gas constant = 8.31436 Joule mole-1 deg-1
T = Temperature, °kelvin
F = Faraday constant = 96488 coulomb/gm-equivalent.
(c means concentration, 1 for inside and 2 for outside.) This potential changes to approximately + 20 mV for a short period during cell depolarization. Cell activity results from some form of stimulation. The Hodgkin - Huxley excitation by stimulus theory was initially postulated (Nobel Prize winners) during the 1950's. This theory is briefly described as follows:
The interior of a cell primarily contains concentrations of sodium and potassium ions.
These concentrations within a cell differ markedly from the concentrations of these ions in the space outside the cells ( FIG. 1). Elementary ionic theory states that, under suitable conditions, any uneven distribution of ionic concentration in an aqueous solution will result in a potential difference between the regions of different concentration. If, for example, solutions containing unequal concentrations of ions are separated by membrane semi permeable to these ions, a potential will be found to exist ( FIG. 2).
==

FIG. 1 Shows the potential generated ionic concentration difference between
two solutions.
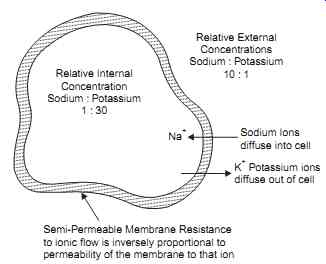
FIG. 2 Shows typical concentration of sodium and Potassium ions within
the cell.
==
1.2. Chemical Gradient
This potential, which is referred to later as the chemical gradient, is given by the Nernst relations : (T = 293°K)
1.2.1. Nernst Relation
Potential (mV) = 61.6 log10 concentration one side of membrane concentration, other side of membrane or for univalent ionic solutions, the Nernst relation simplifies to:
Potential (mV) = 61.6 UV UV
+ where U = Mobility of the negative ions (anions) through the membrane
V = Mobility of the positive ions (cations) through the membrane Referring to Fig. 2, for a 10 :1 activity (concentration) ratio at 37°C, the relative mobilities of chloride and sodium ions are 65.4 and 43.6 respectively. Applying these values to the Nernst relation gives :
This can be confirmed with a voltmeter as shown in FIG. 2. This potential will, of course, run down as diffusion proceeds, unlike that of a living cell.
1.3. Net Gradient
The ionic current produced by ion movement through a semi-permeable membrane depends on the permeability of the membrane and also on the "gradient" that forces the ion through the membrane. This gradient, referred to as the net gradient, consists of both a chemical gradient and an electrical gradient. A chemical gradient is formed due to a difference in concentration producing a potential gradient as given by the Nernst relation. An electrical gradient is formed as a result of a potential that may exist across the membrane due to some other source.
1.4. Cell Concentrations
Experimental investigation have shown that a marked difference in concentrations of both sodium and potassium ions exists across a cell membrane. In mammalian nerve cells as shown in FIG. 1. the concentration of potassium ions is in the vicinity fluid external to the cell. On the other hand, sodium ions are approximately 10 times more concentrated in the fluid external to the cell than in the fluid within the cell.
1.5. Cell in Resting State
Consider a cell in its resting or polarized state ( FIG. 3a). In this state the membrane is moderately permeable to potassium ions, that is, potassium ions can pass fairly readily through the membrane as the membrane offers medium resistance. This membrane is, however, almost impermeable to sodium ions and, thus, offers a high resistance to the passage of these ions. A large net gradient affects the movement of sodium ions into the cell. This net gradient consists of a chemical gradient produced by the 10 to 1 concentration difference between sodium ions on each side of the membrane and a 90mV electrical gradient produced by the standing potential within cell.
==
+ Volt Meter (Reads - 90 mV) Cell membrane Volt Meter (Reads + 20 mV)
+ Electrode external to the cell Sodium ionic current Low permeability Potassium ionic current High permeability Inside of Cell Large Net Sodium Gradient Across Membrane Small Net Potassium Gradient Across Membrane Ionic Current in a Polarized Cell Cell membrane Microelectrode Internal to cell Electrode external to cell Sodium Ionic Current High Sensitivity Potassium Ionic Current Medium Permeability Depolarized cell Low Net Sodium Gradient Across Membrane Large Net Potassium Gradient Across Membrane (a) (b) FIG. 3
==
Net Gradient
The net gradient affecting the movement of potassium ions out of the cell is considerably less than the net sodium gradient. This gradient consists of a large chemical gradient due to the 30 to 1 concentration difference across the membrane; however, this chemical gradient is opposed by the electrical gradient produced by the 90 mV standing potential within the cell.
Thus, although the membrane is almost impermeable to sodium ions, the net sodium gradient is high. Conversely, although the membrane is moderately permeable to potassium ions, the net potassium gradient is low. The net result is that the sodium and potassium currents are equal; the sodium current balances the potassium current with a resultant current of zero.
Since the net current though the membrane is zero, the cell's internal potential will not change and will remain at its - 90 mV resting level.
Indeed, this - 90 mV resting level is determined by the internal cell potential required for sodium and potassium current balance.
Cell Condition after a Stimulus
If the cell receives a stimulus from an outside source, the characteristics of the membrane at the point of stimulation will change and, thus, the ionic currents will also change. After stimulation, the membrane permeability to potassium ions is unaltered but the permeability to sodium ions is increased. A much lower resistance is offered to the flow of sodium ions, thus increasing the sodium ionic current. This increased sodium ionic current causes more positive ions to pass into the cell than are passing out of the cell, causing the internal cell potential to drop from - 90 mV in an attempt to achieve sodium current and potassium current balance.
Cell Depolarization
As this potential decreases, the net sodium gradient across the membrane decreases and the net potassium gradient across the membrane increases, causing the currents to decrease and increase, respectively. This process continues until current balance is again obtained, at which time the internal cell potential is + 20 mV. The cell is then referred to as being in a depolarized state.
Cell Re-polarization
By the time the cell has fully depolarized the characteristics of the membrane have begun to revert back to their pre-stimulus state. This causes the sodium ionic current to be considerably lower than the potassium ionic current; the internal cell potential thus begins to go negative with the process continuing until the - 90 mV resting potential of the cell is once again obtained.
Electrical Analog of the Cell
An electrical analogy to a cell membrane is shown in FIG. 4. This circuit cannot strictly be referred to as an equivalent circuit as the electronic current flow in an electrical circuit and the ionic current flow through a cell membrane cannot be said to be equivalent. After assigning resistance values inversely proportional to the relative permeability of the membrane and assuming potassium and sodium concentration ratios, then the intracellular potential for both a polarized cell and a depolarized cell can be determined. The values assumed are analogous to actual values four in a cell.
Assume:
Relative values for RK RNa and RD are 1 K, 150 K and 0.35 K respectively.
Potassium ion concentration ratio of 30 : 1 inside to outside.
Sodium ion concentration ratio of 10 : 1 outside to inside.
Then,
Ek = 61.6 log 30 1
= 91 mV - by Nernst relation ENa = 61.6 log 10 1
= 62 mV - in opposite polarity to Ek-Nernst
===

FIG. 4. The Electrical analog circuit of the membrane is shown. Cm = membrane
capacitance, ENa Ek are the Sodium potassium Nernst potentials, RK,RNa, the
permeability of membrane to K and Na ions flow through membrane, Rd is the
permeability of membrane to Na ion flow in depolarizing condition.
===
For a polarized cell:
Net potassium current + net sodium current = 0
Net potassium gradient R net sodium gradient RNa k
+ = 0 Potassium Chemical gradient + Potassium Electrical gradient Rk
+ Sodium Chemical gradient + Sodium Electrical gradient
Similarly, for a depolarized cell, RNA is replaced by RD (0.35 K)
Ec
= + 20 mV (Depolarized)
1.6. Action Potential from a Cell
Suppose a microelectrode were inserted into the cell as shown in Figs. 1.3a and 1.3b and a stimulus were applied to the cell, the output of the microelectrode would appear as shown in FIG. 5. This waveform is known as the "Cell action potential". It should be noted that the currents involved in bioelectricity are unlike the currents involved in electronics. Bioelectric currents are due to positive and negative ion movement within a conductive fluid. As these ions possess finite mass and encounter resistance to movement within the fluid their speeds are limited. The cell action potential, thus, shows a finite "rise time" and "fall time".
===
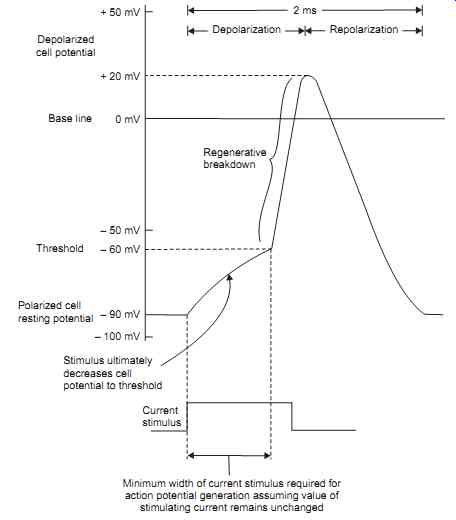
FIG. 5. Shows the Cell action Potential (Internally recorded with Micro-electrode).
===
Sodium Potassium Pump Phenomenon
The ionic concentration gradient across the cell membrane is maintained by virtue of metabolic energy expended by the cell in "Pumping" ions against the ionic gradient formed by the differing ionic concentration between the inside and outside of the cell. This action has been referred to as the "Sodium - potassium pump".
Threshold of Stimulus Causing Action Potential
A cell may be stimulated, or caused to depolarize and then repolarize, by subjecting the cell membrane to an ionic current. This current may be produced by other cells, it may be produced by ionic currents existing as nerve impulses, or it may be artificially produced by some external current stimulus. A cell will be stimulated when sufficient positive ions are added to the inside of the cell to cause its resting potential to be decreased from its - 90 mV level to approximately - 60 mV. Once this threshold level is reached, the cell depolarizes without requiring the addition of any further positive ions to the inside of the cell from the stimulus source. Unless a stimulus above a certain minimum value is received, known as the stimulus threshold, the cell will not be depolarized and no action potential will be generated. The stimulus required to exceed the threshold, the threshold may be exceeded by a short, high-current pulse or by a longer, lower-current pulse.
Refractory Period after excitation
Since the energy associated with the action potential is developed from metabolic processes within the cell itself and not from the stimulus, a finite period of time, known as the refractory finite period of time, known as the refractory period, is required for metabolic processes within the cell to return the cell to its pre-stimulus state. This refractory period has been observed in most cells found in the nervous system. This refractory period has two parts :
The first in which no stimulus, however strong, will cause depolarization (the absolute refractory period) and the second when depolarization occurs only if the stimulus is of more than normal threshold strength (the relative refractory period).
1.6. The Resultant Externally Recorded Action Potential
We have previously discussed the depolarizing and repolarizing action of cells and the resulting potential existing within the cell. As stated earlier, this potential may be recorded with a microelectrode ; however, in most bioelectric measurements, this potential is recorded by electrodes external to the actual cell.
External Electrodes
These external electrodes typically would record the net action of many hundreds of cells, but for the time being, we will consider only a single cell. When recording with external electrodes, an action potential is produced between these electrodes during periods of current flow; that is to say, no potential exists when cells are either in their depolarized or repolarized state. A potential exists only while the cell is changing from one state to another. As the external action potential is generated by the external current that flows during cell activity, the shape of the action potential is related to the variation of this current with time.
External Action Potential
The external potential field rises to its maximum value sometime during the regenerative breakdown phase of the membrane. The external action potential that is recorded from the cell is somewhat similar to a mathematical time derivative of the trans-membrane potential. This potential is detected with maximum amplitude when one electrode is placed as near as possible to the active area and the other electrode is located in a completely inactive or remote area. It is detected with reduced amplitude as the electrodes are placed closer to each other so they intercept smaller elements of potential difference.
Depolarization Current
In a single polarized cell, the inside of the cell is negative with respect to the outside environment, which may be regarded as a reference. As stated previously, the net ionic current flow across the membrane is zero; thus, ionic current flow to and from the cell is zero. If these conditions are altered due to the presence of a stimulating current through the cell membrane, then regenerative membrane breakdown will occur and the cell will depolarize. During the depolarization process the net current through the membrane is not zero; there is a net positive ionic current into the cell through the cell membrane. This current may be detected as a potential difference between two electrodes placed in the vicinity of the cell with the potential difference being produced across the finite resistance of the fluids external to the cell.
This current continues until the cell is fully depolarized, thus, the potential will appear between the two electrodes while the cell is undergoing depolarization. For the short time that the cell exists in a depolarized state, the net current through the membrane is once again zero, thus, no potential will appear between the electrodes.
Repolarization Current
Almost immediately after depolarization, the cell begins to repolarize again. During repolarization, positive ionic current flows from the cell membrane, that is, in the opposite direction to ionic current flow during depolarization. During this period of current flow, a potential will be detected between the electrodes and, since this current is in the opposite direction to the depolarization current, the potential produced between the electrodes during repolarization will be of the opposite polarity to the potential produced during depolarization.
The area included by the depolarization and the repolarization potential waveforms is the same since the quantity of current involved in each process is the same. It should be noted that the process described above is somewhat theoretical as it describes the external action potential generated by single cell. In the following discussion we show that single cell depolarization invariably results in depolarization of the adjacent cells and, hence, this externally recorded action potential will be the net summation of the results obtained from these cells.
1.7. Externally Recorded Action Potential from a Group of Cells, the Travelling Wave of Depolarization
Synchronous Depolarization
The preceding discussion must be modified to allow for many cells in close proximity to one another and to allow for the appreciable length of many of these cells. Consider a group of cells in close proximity to one another, under certain conditions of stimulation, these cells may all depolarize at the same time (synchronous depolarization); however, the repolarization process is random. Repolarization of the individual cells will occur at different times. The resultant externally recorded action potential is shown in FIG. 6. Once again the area included under each wave is the same since the quantity of current involved in each process is the same.
Asynchronous Depolarization
Under other conditions of stimulation, the group of cells described previously will not all depolarize at the same time (asynchronous depolarization). The stimulation may result in one cell depolarizing; the action of this cell depolarizing will then act as a stimulus on its adjacent cell causing it to depolarize also. This chain reaction would proceed until all cells in a particular area have depolarized. The resultant externally recorded action potential would appear as shown in FIG. 6. In practice, combinations of synchronous and asynchronous depolarization occur in a group of cells.
===
 FIG. 6. Shows the stimulation is not synchronous and the potential externally
seen.
FIG. 6. Shows the stimulation is not synchronous and the potential externally
seen.
===
In the same way as the depolarization of one cell causes adjacent cells to depolarize, depolarization of a localized area of an individual cell will cause depolarization of other parts of the same cell. Thus, the depolarization process will appear to travel along the length of the cell causing a travelling wave of depolarization as shown in FIG. 8.
As most bioelectric potentials are recorded as external cell action potentials, the results obtained are a summation of the action of many cells. The action potential wave form may be modified by the number of cells, the shape of these cells, and the type of stimulation applied.
The cell already passing a wave cannot respond to a second stimulus - it has become refractory. But there is a variation in excitability, as at point 3 units in time, a smaller response can depolarize once again, while at a point in time t4, a greater stimulus is required.
The experiments on action potential measurement are usually done on the Squid's axon, which is a large nerve fiber. It is originally called a 100 micron axon. Its action potential varies from - 45 to + 40 mV.
For the Frog's skeletal muscle fiber, it is from - 92 to 30 mV. A contraction follows the wave.
Caridac muscle of frog has a - 55 mV to + 25 mV change, and recovery is prolonged in any cardiac muscle. The top is flat almost.
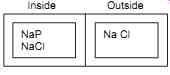
Inside to outside, the concentration of Na+,K+ and Cl
- ions vary in a nerve cell.
The membrane is permeable to Na,Cl but not to Proteins. Therefore, the concentration of Na is greater than in the inside.
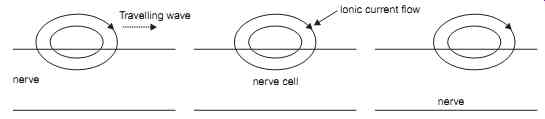
FIG. 8 Showing Electro-tonic conduction as a traveling wave down the nerve.
Nernst Planck Equation
Consider the current flow (in A/s. cm) for diffusion, electrical conduction one by one.
Next