AMAZON multi-meters discounts AMAZON oscilloscope discounts
Table of Contents:
- Introduction
- Parallel Circuits
- Resistors in Parallel
- Voltage and Current in Parallel Circuits
- Review Self-Test Questions
- Series-Parallel Circuits
- Resistance in Series-Parallel Circuits
- Voltage and Current in Series-Parallel Circuits
- Review Self-Test Questions
- Answers to Self-Test Questions
- Lesson Questions
-----------
Lesson Objectives
In this lesson you will:
• Learn how to identify parallel circuits.
• Discover how resistance in parallel behaves differently from resistance in series.
• Learn how to determine voltages and currents in parallel circuits.
• See how combinations of parallel and series circuits work.
INTRODUCTION
Electronic circuits can be connected in two basic ways: in series and in parallel. Because of their simplicity, we have discussed only series circuits so far. In this lesson we will move for ward to parallel circuits. Later you will study circuits in which some parts connect in parallel and other parts connect in series. These combination circuits are called series-parallel circuits. Most pieces of electronic equipment are composed of many combinations of series and parallel circuits.
A 3-bulb floor lamp is a good example of a parallel circuit. Many of these lamps have a 3-position switch. Rotating the switch from the OFF position to the ON position lights one lamp.
The next rotation turns on two lamps. The two lamps are connected in parallel. There is a separate current path through each lamp.
If you rotate the switch once more, all three lamps light. This illustrates the way that current moves in three parallel circuit paths. If one light bulb burns out or is removed, the other two still light. This is because there is an independent path for current flow through each bulb.
If the three bulbs were in series, removing one would keep the other two from lighting, because only one current path would exist. If the current path is broken in a series circuit, there is no path for current flow.
Just as there are rules for series circuits, there are also rules for parallel circuits. In this lesson you'll learn what these rules are, and you'll see how they will help you in future lessons and in your career in electronics. Now let's go ahead with the study of parallel circuits.
PARALLEL CIRCUITS
In a series circuit, the same current flows through all parts of the circuit. A parallel circuit may have a number of different branches, each with a different amount of current flow. If two resistances connect in parallel, there are two paths for current; if three resistances are in parallel, there are three paths for current. The current flowing in each path or branch of the circuit can be, and usually is, different. Let's look at some typical parallel circuits.
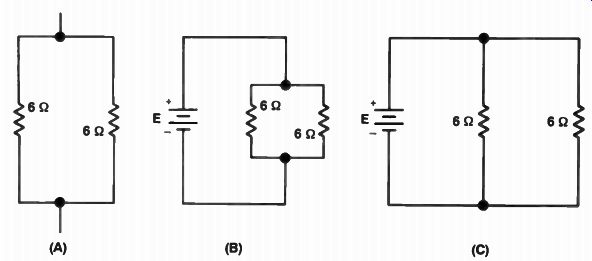
Figure 1. Simple parallel resistor circuits.
Resistors In Parallel
In Fig.1(A) two 6-ohm resistors are connected in parallel. Figure 1(B) shows how these resistors could be connected across a battery. When electrons from the negative terminal of the battery reach the junction of the two resistors, half of the electrons flow through one resistor, and half flow through the other resistor. In this case, the electron flow divides exactly in half, since the two resistors are of equal value. In contrast, resistors of different values would cause a proportional difference in current flow through each parallel branch.
The electrons flowing in each resistor join again at the other junction of the two resistors, and flow back to the positive terminal of the battery Figure 1(C) shows a different way to draw the same circuit, but its difference from the diagram in Fig.1(B) is that it does not indicate a change in the basic operation of the circuit.
Electrons flowing from the negative terminal of the battery divide at the junction; half go through one 6-ohm resistor and half through the other. The two currents join at the other junction, and return to the positive terminal of the battery.
Remember that two 6-ohm resistors in series create a total resistance equal to the sum of the two values, or 12 ohms. What about two 6-ohm resistors connected in parallel? What effect does this have on the total resistance? To find the total resistance of the two 6-ohm resistors connected in parallel, let's first assume that the battery voltage is 6 volts. As you can see, the battery voltage is directly applied across each resistor, so each resistor has a voltage drop equal to 6 volts. This is unlike the case for voltage drops in a series circuit, where the source voltage is distributed among the resistances in the circuit because only one current path exists. Here, each resistance experiences the full force of applied voltage.
With 6 V applied from the battery, the current flow through each resistor will be: E I = - R where I is the current in amperes, E is voltage in volts, and R is resistance in ohms.
1 A 6
Since 1A flows through each resistor, the total current flow in the circuit is 2 amperes. This is an important point to remember: parallel circuits draw more current than series circuits containing the same resistance values. In com parison, a series circuit with two 6-ohm resistors has a total current flow of 0.5 A, or 500 milliamperes.
To find the total resistance in a circuit voltage of 6 V and a current of 2 A, use this formula:
E RT - 1 6 2
« 3 ohms
The resistance of two 6-ohm resistors connected in parallel is 3 ohms. Remember to calculate the total circuit current first, then divide that into the applied voltage to get the total circuit resistance. Each resistor is still 6 ohms individually.
It is the combination of the two in parallel that makes the difference.
Notice that the total resistance becomes exactly half the value of either resistor. This will always be true; when two resistors of equal value are connected in parallel, the total resistance of the parallel combination is half the value of one of the resistors alone.
By the same token, the combined resistance of three equal resistors in parallel is one-third the resistance of one. A parallel connection of four equal-value resistors has one-fourth the resistance of one resistor alone.
The relationships described above hold true for any value of applied voltage. For example, if the battery voltage is 12 V, the current flow through each resistor is 2 A, for a total current of 4 amperes. The resistance is equal to 12 V divided by 4 A, so once again the resistance is 3 ohms.
Unequal Resistances in Parallel. What if the resistors are not equal in value? In Fig.2(A), on the next page, we have a 4-ohm and an 8-ohm resistor connected in parallel. In the circuit shown in Fig.2(B), these two resistors are shown connected to an 8 V battery.
To find the total resistance of the two unequal resistors in parallel, we must again calculate the total current flow. In the branch with the 4-ohm resistance, the current is 2 A, or 8 V divided by 4 ohms. In the other branch the current is 1 A, or 8 V divided by 8 ohms. The total current flow is the sum of the currents in the branches: 2 + 1= 3 amperes. The total resistance of the two resistors in parallel is equal to 8 V divided by 3 A, or approximately 2.67 ohms.
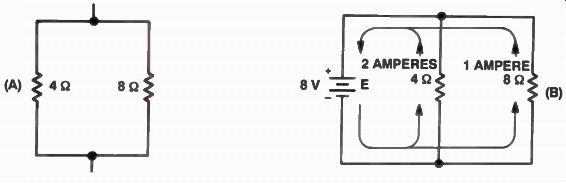
Figure 2. Finding the value of a 4-ohm resistor in parallel with an 8-ohm
resistor.

Figure 3. A parallel circuit with three current paths.
The preceding examples are quite simple: Because the resistance values are low, and it is easy to divide the voltage by the resistance to get the current. However, this is not always the case. For this reason, there is another method of finding the value of resistors in parallel. We use the formula:
R1 x R2 RT = R1 + R2
What you are doing is multiplying the resistor values, and then dividing the result by the sum of the resistor values. For the case of the equal value resistors in the section above, this equation becomes:
6 x 6 36 RT = = = 3 ohms 6 + 6 12
This equation confirms the result of our original calculations from the current and voltage present in the circuit. Let's try the formula on the 4-ohm and 8-ohm resistors from Fig.2.
Here we have:
8 x 4 32 RT =84 = 12 = 2.67 ohms
Multiple Unequal Resistors. Figure 3 shows three resistors connected in parallel. The total resistance in the circuit is found by using the formula for two resistors twice, or by finding the total current flow in the circuit and then using Ohm's law to get the total resistance. Let's do it both ways to check our results. First, let's find the total current that will flow in the circuit from a given battery voltage.
Let's use as an example a voltage of 24 V, which is the lowest voltage that all three resistance values will divide into evenly. Since 24 divided by 6 is 4, the current through the 6-ohm branch is 4 amperes. And 24 divided by 8 is 3, so the current through the 8-ohm branch is 3 amperes. Finally, 24 divided by 12 is 2, so the current flow through the 12-ohm branch is 2 amperes. Therefore, the total current flow in the circuit with a voltage of 24 V applied will be 9 A (4 + 3 + 2 = 9). Now, by using Ohm's law and substituting 24 V for the voltage, and 9 A for the current, we get:
E R = 24 = 9 = 2.67 ohms
Let's solve the same problem using the formula for two resistors in parallel. Group the 6-ohm and the 12-ohm resistors first, and find their parallel resistance. Substituting 6 and 12 in the formula we get: 6 x 12 72 R = 12 =18 = 4 ohms 6 + This means that the total resistance of a 6- and a 12-ohm resistor connected in parallel is 4 ohms.
We can treat this combination as a single 4-ohm resistor and find its resistance in parallel with an 8-ohm resistor. Using the formula we get: 4 x 8 32 R = = 4 + 8 12 = 2.67 ohms
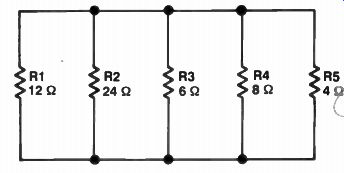
Figure 4. Five resistors in parallel.
Figure 4 shows five resistors in parallel. We can easily find the total resistance of this combination either by assuming a voltage and finding the total current, or by grouping the resistors in groups of two and working out the problem using the parallel resistance formula.
Let's use the latter method first.
Take R1 and R2 and substitute 12 and 24 in the formula. This will give us:
12 x 24 288 R =224 36 = = 8 ohms 1 +
The total resistance of R1 and R2 in parallel is 8 ohms. However, R4 is a single 8-ohm resistor, so R1 and R2 in parallel with R4 are the same as two 8-ohm resistors in parallel. Since the resistance of two equal-value resistors in parallel is half the resistance of one, the total combination of R1, R2, and R4 must be 4 ohms.
By fortunate coincidence, R5 has a resistance of 4 ohms. The 4-ohm combination of R1, R2, and R4 is in parallel with R5, so the total parallel resistance of these four resistors must be 2 ohms.
All we have to do now is find the equivalence of 2 ohms in parallel with 6 ohms. That will be the total resistance of the entire parallel combination. We use the formula to do this: 6 x 2 12 RT = 6 + 2 - 8 = 1.5 ohms Calculating the resistance of many resistors in parallel will not always be as easy as in the previous example. In general, using pair-grouping and the formula is a simple, reliable method of finding parallel resistance. There are usually only two or three resistors involved, so the sys tem works quite well. However, there is another formula for finding the resistance of any number of resistors in parallel. It is a more complicated process, but you may see it in other books, and you should know what it is. The formula is:
RT = 1-1-1- 1 1 R1 + R2 4- R3 4. R4 4. R5
To find the parallel resistance of the five resistors in Fig.4, substitute the value of each resistor in to this formula:
1 RT = 1-1-1- 1-1-1-2 24 6 8 4 1 f
You must find a common denominator for the fractions beneath the division line before they can be added together. (Again, the lowest common denominator is the smallest number into which all the values will divide.) In this case it is 24. So, by using 24 as our lowest common denominator, each fraction is converted to an equal number of twenty-fourths, and the numerators are combined over the common denominator.
To convert to a common denominator, divide the numbers into 24 and put the result above the line. For example, 12 into 24 equals 2, or 2/24.
Similarly, 6 goes into 24 four times, which equals 4/24. Do the same for all the fractions.
RT = 2 + 1 + 4 + 3 + 6 24
After all the fractions have been converted to their common denominator (24), add the top 1 numbers together. The resulting fraction will be 16/24. The formula will now be: 1 RT = 24 To perform the final division, simply convert the fraction to 24/16. Then divide 24 by 16 to get 1.5 ohms. This is the answer you got with the other method.
24 R T - 16 1.5 ohms
Another method is to assume a voltage across the parallel combination, find the total current, and use Ohm's law to get the total parallel resistance. Let's assume a voltage of 24 V, since this is the lowest value you can assume and have each resistance divide into it evenly.
With a voltage of 24 V, the current flow through R1 is 2 amperes. There is 1 A of current through R2, 4 A through R3, 3 A through R4, and 6 A through R5. Thus, the total current flow in the circuit is 16 A (2 + 1 + 4 + 3 + 6 = 16). Now, using Ohm's law, the total resistance turns out to be: E 24 R T = 1.5 ohms Notice that, in each of the preceding examples, the total resistance of resistors connected in parallel is always less than the resistance of the smallest one. This is true because a resistor connected across a voltage source conducts a certain current; if you add another resistor in parallel, regardless of how large a resistance you add, the total current flow in the circuit increases Because you have added a current path. Ohm's law tells you that the resistance is equal to the voltage divided by the current; if the current increases, the effective resistance decreases because the voltage remains the same.
Voltage and Current in Parallel Circuits
In a series circuit, the current is the same in all parts of the circuit. The voltage drop across a part depends upon the resistance of the part. A parallel circuit behaves in an opposite fashion.
Since the parts are all connected in parallel directly across the power source, the voltage drop is the same across all of the parallel parts.
You cannot have two parts connected in parallel and have unequal voltages across them.
Current flow through each branch of a parallel circuit depends upon the resistance in the branch.
The lower the resistance, the higher the current, the higher the resistance, the smaller the current.
Review
When two or more resistors are connected in parallel, the total resistance of the parallel combination is less than the resistance of the smallest resistor. When equal-value resistors are connected in parallel, the total resistance is equal to the individual resistor value divided by the number of resistors. When resistors are connected in parallel, each has the same voltage across it. The current that flows through each resistor depends upon its value. The highest current flows through the smallest resistor.
The combined resistance of parallel resistors can be calculated by assuming an applied voltage, and then dividing the value of each resistor into the voltage to find the branch current. The total current divided into the assumed voltage equals the combined parallel resistance. You can also take the resistors two at a time and use the following formula to find the total resistance of the parallel combination: x R2 RT = R1 + R2
Self-Test Questions
1. What is the total resistance of two 50-ohm resistors connected in parallel?
2. What is the total resistance of a 24-ohm resistor connected in parallel with a 12-ohm resistor?
3. If a 3-ohm and a 4-ohm resistor are connected in parallel across a 12 V battery, what will be the total current flow from the battery? What will be the total resistance of the 3-ohm and 4-ohm resistance in parallel?
4. If two 8-ohm resistors are connected in parallel with a 1000-ohm resistor, what will be the approximate resistance of the parallel combination?
5. In a parallel circuit, the voltage across all branches of the parallel circuit will be , ....
6. In a parallel circuit, the current that flows through each branch of a parallel circuit will depend upon the, . - c of the branch.
The largest current will flow through the branch having the resistance, and the smallest current will flow through the branch having the resistance.
SERIES-PARALLEL CIRCUITS
Series and parallel circuits can be found in all types of electronic equipment. In addition to these two types of circuits, there are many circuits that are combinations of series and parallel circuits.
These circuits are called series-parallel circuits.
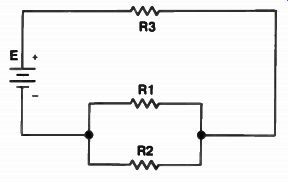
An example of a series-parallel circuit is shown in Fig.5. In this circuit, R2 and R3 are in parallel.
Current flowing in the circuit splits into two smaller currents when it reaches the junction of R2 and R3. The current that flows through each resistor is proportional to the resistance of the branch. If the resistors are equal, half the total current flows through each. On the other hand, if one resistor is much larger than the other, more current flows through the smaller resistor. Also, since the two resistors are in parallel, the same voltage drop is present across each resistor.
The combination of the two parallel resistors R2 and R3 is in series with resistor R1 and the battery. While part of the circuit is a parallel circuit, part of it is a simple series circuit. In the series circuit you have the battery, R1, and the parallel combination of R2 and R3.
In this circuit, electrons leave the negative terminal of the battery and flow through R1. The current divides after leaving R1, and flows through R2 and R3. However, since this parallel combination is in series with R1, the total current flow through R2 and R3 must be equal to the battery current and the current through R1.
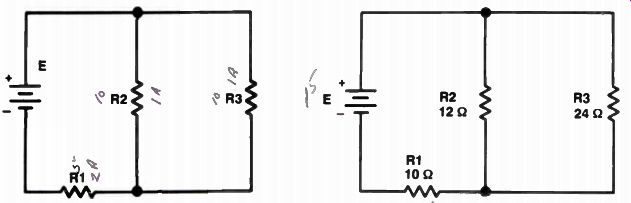
Figure 5. A series-parallel circuit.
Figure 6. A series-parallel circuit with resistance.
Resistance in Series-Parallel Circuits
Figure 6 shows a series-parallel circuit similar to the one in Fig.5. In this example, R1 is the series resistor, with a value of 10 ohms. R2 and R3 form the parallel resistor combination. R2 has a resistance of 12 ohms and R3 has a resistance of 24 ohms. What we want to find is the total resistance in the circuit, since it determines the current flow from the battery First, find the resistance of R2 and R3 in parallel by using this formula: R2 x R3 RP - R2 + R3 Then substitute 12 ohms for R2, and 24 ohms for R3, as shown at the top of the next page.
y 12 x 24 A' P - 12 + 24 288
- 36
= 8 ohms
Therefore, the combined resistance of R2 in parallel with R3 is 8 ohms. For our purposes, R2 and R3 can be replaced by a single 8-ohm resistor, as shown in Fig.7. Notice the symbol used to indicate that R2 is in parallel with R3. The two parallel lines between R2 and R3 mean "in parallel with." This produces an equivalent simple series circuit with a total resistance of 18 ohms. Let's look at a more complicated circuit. Figure 8, on the next page, shows resistor R1 in series with a parallel combination of R2, R3, and R4. R5 is a second series resistor, followed by another parallel combination of R6 and R7. To find the total resistance in the circuit, we first have to find the equivalent series resistance of the parallel pair R6 and R7, plus the equivalent resistance of the R2, R3, and R4 combination.
First, looking at R2, R3, and R4, notice that each resistor is a-eo m resistor. When three equal-value resistors are connected in parallel, the total resistance of the combination is 1/3rd the resistance of any one of the resistors. Therefore, the resistance of this combination is 6 divided by 3, which is 2 ohms. Use formula tsjind the total resist R6 and R7, we get:
12 x 6 R T 12 + 6 72
? 18 - 4 ohms
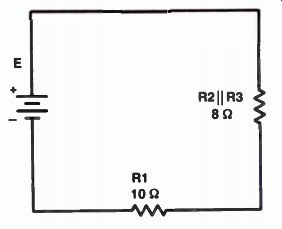
Figure 7. Series equivalent of the circuit in Figure 6.
Now you have a simple series circuit like the one shown in Fig.9, on page 11. To find the total resistance, all you need to do is add the resistance of each resistor:
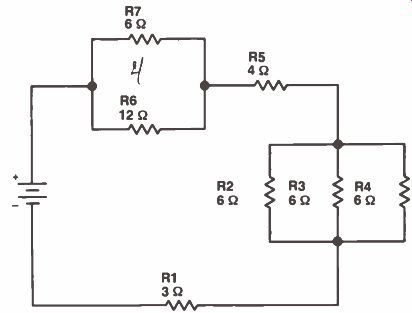
Figure 8. A series-parallel circuit with two series resistors and two
parallel branches.
Voltage and Current in Series-Parallel Circuits
Now let's see how the current divides, and what voltage is across each part of the series parallel circuit shown in Fig. 8. Since the total resistance of the circuit is 13 ohms, let's pick an easy battery voltage so our calculations will come out in whole numbers. Let's assume a battery voltage of 39 volts. With a battery voltage of 39 V and a total circuit resistance of 13 ohms, the total current flow for the entire circuit is provided on the next page.
E I = 39
= 13
= 3 A
This means that the current flow through R1, which is one of the two series resistors, must be 3 amperes. Therefore, the voltage drop across it is: E = IR = 3 x 3 = 9 V
Look at R5, the other series resistor. Current flow through R5 is also 3 A, so the voltage drop across it will be 12 V (3 x 4 = 12). What about the parallel combination of R6 and R7? The value of R6 is 12 ohms, and R7 is 6 ohms. R6 has twice the resistance of R7, so R7 conducts twice as much current. This means that 1 A flows through R6, and 2 A through R7.
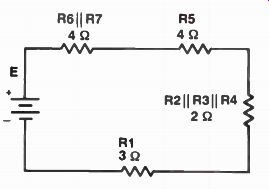
Figure 9. Series equivalent of the circuit in Figure 8.
The voltage drop can be calculated across R6, across R7, or across the resistance of the parallel combination. The current through R6 is 1A, so the voltage drop across it is 12 V (1 x 12 = 12). The current flow through R7 is 2 A, so the voltage drop across it is 12 V (2 x 6 = 12). R6 and R7 in parallel have a resistance of 4 ohms. The current flow through the parallel combination is 3 A, so the voltage drop across the parallel combination is 12 V (3 x 4 = 12). Regardless of which way you calculate it, the answer is the same, as it should be for a parallel combination of resistors.
In the case of the parallel combination of R2, R3, and R4, each resistor carries 1 A of current.
If you multiply 1 A by 6 ohms you get a voltage drop of 6 volts. Using the other method, the parallel combination has an effective resistance of 2 ohms, and carries a combined current of amperes. Again, E = IR = 2 x 3=6 volts. The voltage drop across the parallel combination works out t be 6 V by any method of computation.
Review In a series-parallel circuit, the total current flow is the same in all series branches of the circuit. I the parallel branches, the sum of the currents i the individual branches must be equal to the series current flow. The voltage drop across all components in the parallel branch is the same, and the voltage drop across the series components depend on the resistance of the component and the total current flow in the circuit.
To find the total resistance in a series-parallel circuit, reduce the parallel branch to it equivalent series resistance, and add the series branches to the equivalent resistance of the parallel branches. The total current flow in the circuit can be determined from the source voltage divided by the total resistance of the circuit. The voltage drop across the individual parts in the circuit can be found by Ohm's law.
Self-Test Questions
7. Draw a series-parallel circuit containing a battery and three resistors in which R1 and R2 are in parallel and connected to the negative terminal of the battery, and R3 is a series resistor connected to the positive terminal of the battery.
8. If R1 equals 20 ohms, R2 equals 30 ohms, and R3 equals 12 ohms, find the total resistance in the circuit.
9. Using the values of R1, R2, and R3 for the preceding problem, if the battery voltage is 48 V, find the voltage drop across each resistor and the current flow through each resistor in the circuit.
10. If, in a circuit like the one shown on page 8 in Fig.5, R1 equals 5 ohms, R2 equals 10 ohms, and R3 equals 10 ohms, what is the source voltage if the current through R2 is 1 ampere?
ANSWERS TO SELF-TEST QUESTIONS
1. 25 ohms. The total resistance of two equal resistors connected in parallel is always one half the resistance of either resistor.
2. 8 ohms. You find the resistance of the two resistors in parallel by using the formula:
RT = R1 + R2 Substituting 24 ohms and 12 ohms for R1 and R2 you get: R1 x R2 24 x 12 RT = 24 + 12 288 = 36 = 8 ohms 3 The current flow through each resistor can be found from Ohm's law: E I = É The current through the 3-ohm resistor will be: I . - 12 = 4 A
3. The current through the 4-ohm resistor will be: 12 I = - 4 - 3 A
The total current flow will be the sum of these two currents: 7 amperes. You can use this value of current and the voltage of 12 V to find the resistance of the two resistors in parallel. (See the formula at the top of the next column.)
R = I = - 12 = 1.7 ohms 7
4. Slightly less than 4 ohms. The resistance of two 8-ohm resistors in parallel will be 4 ohms - half the resistance of either resistor. The 1000-ohm resistor is so large that we can almost ignore it because it will not appreciably affect the total resistance of this circuit. However, it will reduce it slightly below 4 ohms; the exact value would be about 3.98 ohms. If you said 4 ohms is the correct answer rather than slightly below 4 ohms, you are close enough.
5. In a parallel circuit, the voltage across all branches of the parallel circuit will be the same.
6. In a parallel circuit, the currents through each branch of the parallel circuit will depend upon the resistance of each branch. The largest current will flow through the branch having the lowest resistance, and the smallest current will flow through the branch having the highest resistance.
7.-----------
8. 24 ohms. The total resistance of the parallel combination of R1 and R2 can be found from the parallel resistor formula. Substituting these values we get:
RT = 20 + 30 20 x 30 600 50 =12 ohms
This resistance is in series with R3, which also has a resistance of 12 ohms, so the total resistance of the circuit is 24 ohms.
9. With a voltage of 48 V and a total resistance of 24 ohms, the current flowing in the circuit will be: 48 I = = 2 A 24
This means that the voltage drop across R3 will be:
E = 2 x 12 =24 V
Therefore, the voltage dropped across the parallel combination of R1 and R2 must also be 24 volts.
The current through R1 must be: 24 I = = 1.2 A 20.
The current through R2 must be: 24 I = = 0.8 A 30 10 20 volts.
If the current through R2 is 1 A, and the resistance of R2 is 10 ohms, the voltage across R2 must be: E = 1 x 10 = 10 V
Since R2 and R3 are in parallel, the same voltage must be across R3, and therefore, the current R3 must also be 1 ampere. This means the total current must be 2 A, so the voltage across R1 must be: E = 2 x 5 = 10 V
Therefore, the source voltage must be 20 V (10 + 10 = 20).
----------------
Lesson Summary
Some of the important facts that you should remember about this lesson are:
• Parallel circuits provide multiple paths for current flow.
• Adding resistance in parallel decreases the total resistance of the circuit.
• The same voltage exists across parallel circuit branches, but the current may be different in each branch.
• Parallel circuits can be in series with other parallel networks in the same circuit.
LESSON QUESTIONS
This is Lesson Number 2219.
Make sure you print your name, student number, and lesson number in the space provided on the Lesson Answer Form. Be sure to fill in the circles beneath your student number and lesson number.
Reminder: A properly completed Lesson Answer Form allows us to evaluate your answers and speed the results and additional study material to you as soon as possible. Do not hold your Lesson Answer Forms to send several at one time. You may run out of study material if you do not send your answers for evaluation promptly.
1. The total resistance of three 15-ohm resistors connected in parallel is:
a. 45 ohms.
b. 30 ohms.
c. 15 ohms.
d. 5 ohms.
2. If one 9-ohm, one 18-ohm, and two 24-ohm resistors are all connected in parallel, the resistance of the parallel combination will be:
a. 2 ohms.
b. 3 ohms.
c. 4 ohms.
d. 6 ohms.
3. R1 and R2 are two resistors of the same value connected in parallel. This parallel combination is connected in series with R3, a 10-ohm resistor. The series-parallel network is connected to a 15 V battery. If the voltage across R3 is 10 V, what are the values of R1 and R2?
a. 5 ohms.
b. 10 ohms.
c. 15 ohms.
d. 20 ohms.
4. When two unequal resistors are connected in parallel across a battery, the voltage drop across the two will be:
a. Equal to the battery voltage.
b. Greater across the larger resistor.
e Greater across the smaller resistor.
d. Zero.
5. Resistors R1 and R2 are connected in parallel. The resistance of R1 is 5 ohms, and the current through it is 2 amperes. The current through R2 is 0.5 A, and the resistance of R? is:
a. 5 ohms.
b. 10 ohms.
c. 15 ohms.
d. 20 ohms.
6. Three 6-ohm resistors are connected in parallel. A fourth 6-ohm resistor is connected in series with the parallel combination. The series-parallel network is connected to a battery. If the voltage drop across the series 6-ohm resistor is 6 V, the voltage drop across the parallel-connected 6-ohm resistor combination is:
a. 2 volts.
b. 3 volts.
c. 6 volts.
d. 18 volts.
7. In the circuit shown below, the battery voltage is:
a. 4 volts.
b. 6 volts.
c. 8 volts.
d. 10 volts.
8. If a 10-ohm, a 100-ohm, a 1000-ohm, and a 10,000-ohm resistor are connected in parallel, the total resistance of the parallel combination will be:
a. Greater than 10 ohms.
b. 10 ohms.
Less than 10 ohms.
d. Approximately 100 ohms.
9. If a 100-ohm resistor is connected in series with three 100-ohm resistors that are connected in parallel, the total resistance of the series-parallel combination will be:
a.Greater than 100 ohms.
b. 100 ohms.
c. Less than 100 ohms
d. 400 ohms.
10. In the circuit shown below, if the voltage across R1 is 10 V, the voltage across the parallel combination of R2, R3, and R4 will be:
a. Greater than 10 volts.
b. 10 volts.
c. Less than 10 volts.
d. 30 volts.
----------------

NRI Schools
NOTHING SUCCEEDS LIKE SUCCESS
"How can I be a success?" The simplest answer to this question is "Finish what you start." Until you have achieved success, the individual tasks facing you are relatively unimportant in themselves. The important thing is the effect they have on you, what you learn from them, the practice they give you in succeeding at what you do.
It's easy to find reasons for quitting, especially when things get tough, but what do we accomplish if we do things the easy way? What can we possibly learn by quitting? We only learn how to quit--how to fail.
If success in any undertaking depends on effort (and we all know it does) then the more effort we put into an undertaking, the greater our success will be. You may not be able to detect the potential success present in every individual effort, but it is there. You have to keep in mind, as you take each step, that success can't be reached in one leap; it has to be approached strategically, carefully, and one step at a time.
"Nothing succeeds like success." What does the old saying mean? Simply that each success paves the way for future successes. Failure is merely a failure of effort--giving up too easily. You can't really fail unless you quit trying, so stick with each job until you win, and can add it to your list of successes. It's not the jobs themselves that make the success: it's what you do with them, what you take from them to the next job.
---------------------------