Author: Roger Anderson [Assistant Chief Engineer Shure Brothers, Inc. Evanston, Ill. ]

Rare is the audiophile who has not encountered a quantity known variously as "equivalent mass," "effective mass," "tip mass," or some similar combination of words in the specifications for a phono pickup cartridge. The context in which this term is used shows that "smaller is better," but no one has bothered to either explain or define the quantity.
From the figures which are sometimes quoted, it seems that this confusion may sometimes be intentional, since an absence of formal definition would permit each user to define it to his own advantage. This article will look at the basic idea of equivalent mass and show how to calculate a number consistent with the basic concept.
Additionally, equivalent mass analyses of several popular pickups will be presented.
One may wonder why there should be such great concern over mass--especially fractions of one milligram, which is about the weight of 3/16 inch square of magazine paper. The reason lies in the fact that the maximum driving force available from a phonograph record groove wall cannot exceed 0.7 times the stylus force without losing contact between the tip and groove wall (see Appendix I). At high frequencies, much of the force required from the groove wall is needed to vibrate the mass (or weight) of the particular moving system of that pickup.
Imagine a weight as in Fig. 1 (say 1 lb.), hanging from a long string. Now move the weight back and forth over a fixed distance (6 inches, for instance). For a one -second oscillation, only a mild force is required, but the maximum force required will be in direct proportion to the square of the number of oscillations per second. In other words, 100 oscillations per second will require 10,000 times more force, than one oscillation per second.
Consequently, forces which are insignificant at one frequency may well be overwhelming at a higher frequency. The maximum force (F) required to oscillate a mass with simple sinusoidal motion may be calculated from the formula:
F = KMaf^2 (1)
where: f equals oscillation/sec, a equals total amplitude, K equals constant, and M equals mass.
This formula gives the force required when the force is applied directly to the weight. However, the force requirements may change drastically if a mechanical system is interposed between the driver and the weight. Figure 2 shows the weight driven through a lever system whose own weight may be ignored for this initial analysis. At point 1, the mass obviously looks to the driver like 1 lb., but the situation is more complicated at point 2. We can analyze point 2 by rearranging formula 1 above:
M= F/Kt^2 a
Let us designate conditions at point 1 with the subscript ,, then
M1= F1/Kt^2 a1
...using subscript 2 at point 2,
M12= F2/Kt^2 a2
Since we are dealing with the same units and frequency at both points, K and f will be the same. Because F is transformed by a 2:1 lever, F, will be 1/2 of F, and a 2 will be twice a,. Substituting:
…but is M,; therefore M2 = 4M,. i F1
Consequently driving the mass through a 2:1 lever decreased the apparent mass to 1/4 its former value.
Thus, the geometry of a moving system has a profound effect on the apparent mass presented at the driving point.
In practical structures, the mass of any levers must also be considered.
The moving system of a phono pickup will typically consist of a metal tube with a diamond tip at one end and one or more transducer elements at the other end, all supported in a pivot arrangement. This structure seems quite complex to evaluate.
-----TOTAL OSCILLATION AMPLITUDE
Fortunately, this situation was investigated long ago by mechanical engineers who determined that the property of a rigid body to react to rotary motion is expressed by a number termed the "moment of inertia." This quantity is determined by subdividing the body into many small parts, multiplying the mass of each part by the square of its distance to the pivot, and adding all the resulting products. It is apparent from this definition that the mass of a concentrated body having the same reaction to rotary motion (moment of inertia) as the original rigid body may be calculated by dividing the moment of inertia by the square of the distance from the pivot to the driving point.
This mass of an equivalent concentrated body is termed the equivalent or effective mass of the original body referred to the driving point. In the case of a phono pickup, the driving point is the stylus, and the pivot is the center of the elastomer bearing or the flexible portion of the tie wire.
Thus, the quantity originally known as the "equivalent mass of the moving system referred to the stylus tip" has become "equivalent mass," "tip mass," or just "mass," and has lost much of its precision and usefulness in the process.

Fig. 2--The oscillating mass with lever drive.
How is Equivalent Mass Calculated?
As an example, consider an aluminum tube typically used for a stylus cantilever member (shank) shown in Fig. 3.
The first step is to find the area of cross section which is done by subtracting the area of the inner circle from the outer:
A = π(R2 r2) = 0.0000534 in2.
where R = outer radius = 0.009 in. and r = inner radius = 0.008 in.
The volume is obtained by multiplying the area by the length:
V = AL = 0.0000534/0.220 = 0.00001174 in3.
where: L = length
Converting to metric (1 in.= 2.54 cm):
Vcm3 = V(2.54)3 = 0.0001924 cm3 .
The mass is found by multiplying the volume by density (density for aluminum is 2.7 grams/cm'); M= Vd = 0.0005194 grams.
The moment of inertia, I,, about the center of the body is now calculated using reference formulas found in mechanical engineering books. The American Institute of Physics Handbook gives the following equation for a hollow cylinder about its center of gravity:
= 0.00001364 gram cm2 0.220
using the values shown above for M, L, R, and r.
However, the pivot is actually 0.125 in. from the center of gravity, so an additional quantity must be added:
4(3 +R2+r2)(2.54)2
Ip = Md2 = 0.0005194 (0.125)2 (2.54)2
= 0.00005235 gm cm2
where: d=distance from the center of gravity to the pivot.
The total moment of inertia is the sum of the above:
It = lc + Ip = 0.00006599
The equivalent mass contribution at the stylus tip is found by dividing by the stylus tip -to -pivot distance squared:
Shank Meq = Ií/(0.235)2 (2.54)2
=0.000185 grams = 0.185 mg
Each of the quantities in Table I is calculated in the same manner, with the exception of the stylus tip, which may be added directly.
Results
In Table I, the equivalent mass analysis is shown for four popular phono pickups. A is a moving -iron type, B is a moving-magnet type, C is a dual moving-magnet type, and D is also a moving-iron type. Comparison of the last two columns emphasizes the fact that the mass (as would be ¡treasured on a scale) is quite different from the equivalent mass. For instance, a ranking in terms of mass would be D lowest, then A, and B, with C heaviest at about two times greater than D. However, the equivalent mass ranking would be B lowest, then A, then C, and D. D is more than twice the equivalent mass of B! Consequently, impressions of relative size or measurements of mass can be quite misleading when compared to the equivalent mass, and this is well known by most pickup designers. The individual contributions of the component parts of each structure are also tabulated, both in equivalent mass, and as a percentage of the total.
This parts breakdown illustrates some surprising facts. By intuition, one might expect that the transducer element (magnet or armature) would contribute a large part of the total equivalent mass since it is made of heavy material, but this is not the case in three of the four structures. Furthermore, the type with the greatest equivalent mass contribution from the transducer element is a moving-iron type, where the magnetic field is supplied by a stationary magnet.
In the three other types, B, C, and D, the largest single contributor of equivalent mass is the shank, perhaps suggesting that further reductions might be possible in this area. The shank, rather than the transducer principle, might be seen as the most limiting present problem since it is common to practically all pickups.
It is also interesting to note that the diamond tip contributes only 6 to 10 percent of the total, and that the diameter of the tip influences this equivalent mass much more than the length.
Now that the definition and distribution of equivalent mass has been discussed, the item which remains is its significance. It is apparent that the equivalent mass is a calculated, not a measured parameter, since it does not lend itself to direct measurement. How can this number be related to a measured parameter of performance? The answer can be found in the tracking ability curve of the pickup (trackability for short). This curve is shown in Fig. 4 and is determined by finding the velocity at which the pickup mistracks for each frequency of interest. The curve thus defines the boundary between the operating and mistracking area on the curve. From Equation 1 and Appendix 1, we can construct a line on the trackability curve which represents the theoretical trackability of an equivalent concentrated mass. That is, if the pickup had no mechanical characteristics other than its equivalent mass, its trackability should match the theoretical line on the trackability graph.
Of course, the gap between the theoretical line and the measured performance represents the extent to which other mechanical characteristics influence the performance of the pickup. Incidentally, the frequently observed effect of a flexibility in the drive system is to cause a resonance to appear which decreases the actual trackability! The calculated equivalent mass forms a simplified reference point on the high-frequency tracking performance of the pickup, and the difference between this idealized reference and the measured track ability is an indication of the extent to which other mechanical characteristics affect the performance.
Predicting the performance of a pickup from equivalent mass figures ignores the substantial difference between simplistic theory and delivered performance. A measurement of track ability, on the other hand, is a statement of delivered performance which involves no wishful assumptions.
Equivalent mass is an abstract concept which may, nevertheless, be calculated in a straightforward and well-defined manner and is easily distinguished from "mass." It has been periodically abused due (I suppose) to ignorance or poetic license, however, the equivalent mass is only one factor among many which determines the high -frequency performance of a pickup.
Therefore, the answer to the original question "Equivalent Mass-Fact or Fiction?" must be an emphatic "Yes!"

Fig. 3--Typical shank for a stylus assembly.

Fig 4--Trackability characteristic of the V15 Mk III phono cartridge.
-----------------
Appendix
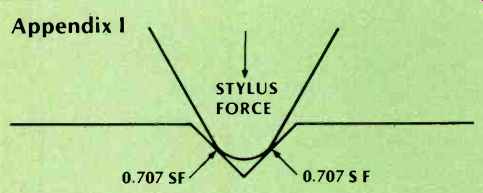
--STYLUS FORCE; 0.707SF 0.707S F
When a stylus tip interacts with a groove, two reaction forces are generated at the two points of contact. If either of these forces becomes zero, the tip looses contact and, therefore, positive guidances and mistracking results.
Therefore, for the case of 45° modulation, dynamic forces greater than 0.7 times the stylus force will cause a reaction force to become zero. Vertical and lateral modulation may be resolved into simultaneous 45° modulation components, and each component examined to test for the 0.7 F criteria.
Appendix II
The theoretical trackability of a concentrated mass may be calculated from the Newtonian relation:
F = ma/980,000
where: F equals the force in grams, m equals the mass in milligrams, and a equals the acceleration in cm/sec'. However, in sinusoidal motion,
a = 2/rfv
where: f equals the frequency in Hz and v equals the velocity in cm/sec.
F is supplied by the groove wall and is limited to 0.707 of the stylus force SF.
Substituting: 0.707 SF = 2irfmv/980,000
Solving for v: v = 110,272 SF / fm
Example: The V15 Type III has an equivalent mass of 0.34 mg. What is the trackability of this concentrated mass at 1 gram stylus force?
v= [110,272 x 1] / [10,000 x .34] = 32.43 cm/sec
This point is plotted on the graph in Fig. 4. When the frequency is doubled, the trackability is halved, and vice versa.

Equivalent Mass Comparison
NOTE: These calculations are based on dimensions which involve estimation and should be considered approximate.
(Source: Audio magazine, March. 1978, )
= = = =