Harvard University found in 1895 that its newly completed Fogg Art Museum had severe acoustical difficulties. President Eliot, head of the university, turned to a young physics professor named Wallace Clement Sabine with the request to "do something" about the problem.
Sabine didn't follow the practices of past generations and hang draperies, place carpets, etc., to "deaden" such a "live" room. Instead he turned from qualitative approaches in finding the solution to a study of the problem on a quantitative basis.
Sabine had at his disposal a number of useful tools to aid in the investigation of the problem. First, there was the troubled lecture room in the Fogg museum. Second, there was nearby Saunders Theater which was considered to have excellent acoustics. Third, the constant-temperature room in the sub-basement of the Jefferson Physical Laboratory turned out to be a reverberation chamber. Finally, he had a middleof-the-road room considered acoustically tolerable, but not much more, in the large lecture room, also in the Jefferson Physical Laboratory building.
With these environments as laboratories, Sabine used the seat cushions from Saunders Theater as his portable absorption, organ pipes and a portable windchest as his sound source, and a stopwatch and his own remarkable hearing as his acoustic test instruments.
After more than two years of intensive research (he often taught classes during the day and did research all night, existing on just a few hours of sleep), Sabine not only had corrected the troubled room by adding the correct amount of acoustical absorption, but as it turned out, he had gathered the raw data for the first important breakthrough in the science of architectural acoustics.
One Saturday evening on the 29th of October, 1898, staring at some of his curves, Sabine called out to his mother (who was living with him at the time),"Mother, it's a hyperbola!" This simple, but inspired observation, took architectural acoustics out of the dark ages of cut-and-try into the sunlight of calculation and measurement.
The insight that came to Sabine, revealing the fundamental relationship between the size of a room and the absorption needed, resulted from his unbelievably precise measurements coupled with his intuitive genius. Thereafter, the reverberation time of a room was calculable prior to construction.
In September, 1975, some 77 years later, W. B. Joyce, in an article entitled, Sabine's Reverberation Time and Ergodic Auditoriums in the Journal of the Acoustical Society of America, showed the relationship between the second law of thermodynamics and Sabine's equation. This talented Bell Laboratories scientist derived Sabine's equation from a literature search that could have been done at Sabine's time since the necessary thermodynamic concepts were extant by 1895. (For those with a desire to experience the original material on this subject, there is no substitute for obtaining and reading the first two references in the bibliography.) In 1929, M.J.O. Strutt considered reverberation by regarding itasa case of free damped vibration of the volume of the air enclosed in a room (this was before computers, mind you). The analysis involves the general wave equations, with suitable boundary conditions imposed. Strutt regarded as unsatisfactory the theories which dealt with the paths of separate sound rays (geometric acoustics). The various eigen tones or modes of the resonant vibration of the air columns in the room appear in the analysis. This analysis revealed Sabine's law as an asymptotic property toward which the reverberation tends, as the frequency of the (forcing) sound becomes infinitely great compared with the lowest free frequency of the air itself-in other words, when the dimensions of the room become infinitely great compared with the wavelength of the sounds.
Later work at MIT by Philip Morse and Richard Bolt led to the honest but humorous conclusion that "The practical role of wave acoustics is that it can indicate how to design an enclosure for which geometrical acoustics and statistical acoustics are valid, and in which there is no need of wave acoustics." In any enclosed space, either rooms that people can live in or boxes that house loudspeakers, there is a finite length of time required for any steady state sound field, developed by a sound source, to die once the sound source is turned off. All of us have experienced the duration of sound after a handclap in a concrete structure, such as an underground parking garage, compared to the same handclap in an open field.
The sound heard during the length of time it takes the initial sound (e.g. handclap) to die out is called reverberation. The reverberation time is the length of time, in seconds, that reverberation can be heard. In precise measurements, the reverberation time is measured for at least 20 dB of decay and then extrapolated to give the time it would have taken to decay 60 dB. This time in seconds is called the RT60.

Fig. 1-Measuring the RT60 of an enclosure.

Fig. 2-The chart recorder method of measuring RT60.
Figure 1 illustrates the typical measurement setup. A band of pink noise (typically either octave or 1/3 octave) is emitted by the loudspeaker until a steady state level is produced in the enclosure (i.e. the rate of acoustic power being emitted is all being absorbed at the same rate). Then the amplifier output switch is opened and the microphone signal is fed to another band-pass filter identical to the send filter, and the decay rate is observed on the display unit (which may be a digital meter, a graphic level recorder, or an oscilloscope screen). When a graphic level recorder is used, Fig. 2 shows how the trace produced is analyzed.
The Law of Conservation of Energy
The basic law of the conservation of energy states that "energy can be transformed but it is never created or destroyed." Thus, the rate of increase of reverberant energy (Wait t) in a room must equal the rate of emission of energy from the source into the reverberant sound field (WaT |) minus the rate of absorption of the reverberant energy, Sa |.

This means that all of the energy a sound source puts into an enclosure must be accounted for by either absorption (turning into heat), by transmission (passing through the enclosure to another space), or by reflection (adding to the sound level).
Sound Levels Emitted By Sound Sources
Looking at how the sound power is calculated, we find that if we were to place at the center of an imaginary sphere with a radius of 0.282 M an omnidirectional sound source of negligible size which emitted one acoustic watt, we could by internationally agreed upon definition write:

Where: dBwa is the acoustic power expressed in dB ref erenced to one pico-watt.
If we were to examine the situation carefully, we find that for a sphere with a radius of 0.282 M, the surface area would be 1 M2. (4πr2 =A). Therefore, our acoustic intensity is 1 W/M2.
The intensity may also be expressed as a level in dB. We can write:

Since dBp also has an internationally agreed upon reference value (0.00002 Pascals or 20µPA), the sound pressure is

Another way of approaching the sound pressure value is to observe that the average pressure is

which is a form of acoustic Ohm's law, Where Wa is the acoustic power in watts;
Pc is the acoustic impedance in Rayls. (N-Sec/M3) and is 406 MKS Rayls-when T =22°C(71.6°F), atmos. press. = 29.6 inches Hg or 0.75/M Hg;
ρ is the density of air in Kg/M3 and c is the velocity of sound in M/Sec, and 4πr2 = area of a spherical surface and acts as a form of acoustic power factor.
Thus:

To summarize these calculations, we can construct the following relationships for our 1 acoustic watt radiating omni-directionally and measured at 0.282 M:

The inner sphere of Fig. 3 represents these values.
Now let's change only a single parameter and double the radius of our sphere. First of all, we can, by inspection, detect that our spherical surface area quadruples when the radius is doubled because the radius in the area formula is squared.
We then have four square meters of surface area. This means that we have only 1/4 of a watt per square meter, even though adding the 4 areas together still leaves us with 1 acoustic watt of total power.

Therefore, our acoustic intensity level and our sound pressure level have lowered from 120 dB to
120 + (-6.02) = 113.98 dB
Our sound power level, however, remains 120 dB, while the acoustic power = 1W = 120 dB, the acoustic intensity = 1/4 W/M2 = 113.98 dB, and the acoustic sound pressure = 10.08 PA = 113.98 dB. This effect is called the inverse square law rate of level change.
From this example, it can be seen that, neglecting true attenuation factors (such as absorption), sound level decreases as the square of the distance from the sound source and would in a free field finally spread out sufficiently to become inaudible. Figure 4A illustrates the area change per doubling of distance. This effect is dependent upon two angles both diverging (see Fig. 4B). When only one of the two angles diverges, then the area changes are directly related to the radius change and only -3dB/doubling occurs (see Fig. 4C)
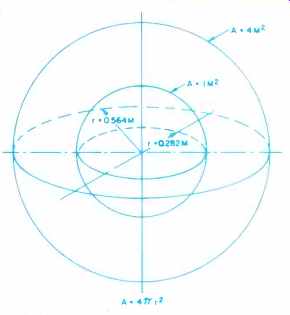
Fig. 3-The relationship of the spherical surface area to radius.
The Effect of Directivity on the Data
If we were to go back to our original sphere with a radius of 0.282 M, and this time change another single parameter such as the surface area of the sphere from a sphere to a hemisphere, we could then re-inspect our data as follows:
Acoustic power = 1W = 120 dB, the Acoustic intensity = 2W/M2 = 123.01 dB, and the Acoustic sound pressure = 40PA = 123.01 dB. All of this because our 1 acoustic watt now passes through 0.5 M2 of surface at the distance of 0.282 M. The parameter name for this effect is Q or directivity factor

* relative power for hemisphere surface, relative power for rear of hemisphere.
Therefore:

Confining the Acoustic Energy
Nekt let's confine this source emitting 1 acoustic watt in an enclosed space having and internal volume of V = 500,000 ft3 (14,160 M3), a boundary surface area of S = 42,500 ft2 (3948.25 M2), and with each surface reflecting 85 per cent of the energy and absorbing 15 per cent. Therefore, our absorption coefficient is 15/100 = 0.15.
We now have direct sound-that sound energy which has been emitted but has not yet encountered a boundary, and reverberant sound-that sound which has encountered a boundary and reflected and is now mixed with all other sounds that have reflected one or more times.
The Hopkins-Stryker Equation
The level present as direct sound at any given distance can be found by

(And the level present as reverberant sound becomes...)
Combined, these two equations become the equation that allows the total dBpT to be calculated:

...when r is in ft.
Now, let's again gather our data; the Acoustic power = 1W
= 120 dB, the acoustic intensity has become complex as a result of many reflections combining, and the reverberant sound field acoustic pressure = 1.68 PA = 98.5 dB. One acoustic watt is a powerful level, as can be seen in Fig. 5. We now have a reverberant sound field at a level of 98.5 dB. If we were to turn the sound source off at this point and time the decay to 98.5 60 = 38.5 dB, we would be able to measure the RT60. Let's instead calculate it from a completely theoretical basis.
Derivation of the Sabine Equation
It is easily understood that the larger the internal volume possessed by an enclosure, the more energy it can hold without the walls bulging (much as a larger bucket can hold more water than a small bucket). Therefore, RT is proportional to V. Looked at from another viewpoint, if we cut an "open window" in our large enclosure, energy can flow out.
The rate at which it flows out (the RT) is proportional to 1/a where a is the average absorption of the opening.
As the sound waves are emitted and encounter boundary surfaces, there will, after sufficient encounters, develop a mean distance between encounters. This distance, called the mean free path, M.F.P., is found by
M.F.P. = 4V /S

Fig. 4A-The area increases as the square of the radius.

Fig. 4B-The area increases as the square of the radius when both angles
diverge.

Fig. 4C-The area increases as the radius increases when only one angle
diverges.

Fig. 5-The near field, free field, far field, and reverberant field
represented graphically.

Fig. 6--The absorption of a steady-state sound field.
The M.F.P. concept has been rigorously demonstrated both mathematically and empirically. If we assume the speed of sound to be 1130 Ft/Sec., then it is possible to say that the number of reflections per second, R.P.S., is:

Further, if we are concerned with 60 dB of decay, where e (6 1n 10) = 1,000,000 (as -60 dB is 1/1,000,000), then 6 1n 10 (1/a) has to be the total number of reflections, N, during 60 dB of decay (See Fig. 6).
It can be intuitively seen that:

[Writing the components in the form given just above:
... can be collected into ...]
*speed of sound in Meters/Sec, **metric constant.
How fascinating it is to find out that the constant Sabine worked out from his plotted data was 0.049.
Around 1930 efforts were expended to "improve" the Sabine equation for the limiting case of very high absorption, and it was rewritten as the Norris-Eyring equation

-1n (1 -a) converts any a found by measuring the RTC of a real room and obtaining a by

Joyce's paper is so thorough on the invalidity of the NorrisEyring equation (where it is shown that the high Absorptitivity case is such a grossly underspecified problem that none of the geometric equations can be solved correctly) that we suggest that those readers with questions in this direction start with Joyce's paper.
The Fitzroy Equation
Dariel Fitzroy, a quiet, competent thinker, recognized during the late 1950s that in enclosures where the absorption was not uniform, the RT60 measured was greater than the RT60, calculated. He reasoned that there could be three typical axes for reverberation-floor-ceiling reflections, end wall-to end-wall reflections, and side-wall-to-side-wall reflections, and he wrote his equation to account for such a case:

The Fitzroy equation has proven to have remarkable applicability in the real case of, say, a carpeted floor, acoustic tile ceiling, and with all other surfaces highly reflective.
Having used this equation to predict an RT60, then the a for treatment purposes can be looked at by

Limitations To All Acoustic Equations Based On Geometry and Statistics
It should always be considered that, insofar as the reverberation formulas depend upon statistical averages, they presuppose a complete mixing of sound in the room. In very absorptive rooms, the sound dies away in a few reflections, and the statistical basis of the formulae is weakened. In recent studies done by me with time delay spectrometry, typical meeting rooms in hotels have been found in some cases (RTC <0.5 Sec) to develop no reverberant sound field, whereas in others RT60 >0.7 Sec a field appears.
My experience with time delay spectrometry causes me to state unequivocally that recording studio control rooms are not proper subjects for use of classic statistical equations.
In very large rooms, such as the Astrodome and the Superdome, because the sound cannot cross the room many times during a measured reverberation period of a few seconds, the validity of the formula is affected. I hope to have much fundamental work to report in the not too distant future on the guidelines TDS has illuminated with regard to reverberation in such spaces.
Absorption Units
All materials, whether intended for acoustical use or not, have absorption coefficients that have to be accounted for in RT60 calculations. Just a few of these are shown in Table 1.

above: Table I --Sound-Absorption Coefficients of General Building Materials
and Furnishings
The unit of absorption in the United States is the sabin (named in honor of W. C. Sabine). One sabin is 1 ft2 of open window. In Europe the absorption unit is also called a sabin, but it is 1 M2 of open window. To find the number of sabins of absorption in an enclosure, each area of boundary surface is subdivided into as many parts as there are differing absorptive materials. The average absorption coefficient, a, is found by
Saobj is the number of objects in the space times the Sä rating. See Table II for examples.
Reams of paper have been expended in advocating various methods of measurement. Broadly classified, the major techniques are: Where sources are 1) interrupted warble tone, 2) interrupted random noise, 3) the Schroeder-Kuttruff method (the ringing of a pulsed filter is employed as a signal source), and 4) gunshots, bursting balloons, and other impulse sources.
Readout devices are 1) high speed graphic level records, 2) digital direct-reading meters, 3) oscilloscopes with logarithmic vertical scales and either long persistence screens or memory, and 4) well-trained ears and a stopwatch.
Today, with the advent of digital real-time analyzers and readily available, powerful, table-top computer-calculators, it is possible to fully automate these measurements. Again, thanks to the increasing power of computers, the wave acoustics solutions may become realistic in small, readily available devices within the coming decade. The important point is that the correct philosophy be attached to the automation, as the rule GIGO (garbage in -garbage out) still applies.
No effort has been made in this article to discuss the acceptable criteria for reverberation developed during the past 70 years nor of the basic approaches to using the equations in the planning for the application of acoustic absorption to spaces as correctional measures.

above: Table II -- Absorption of Seats and Audience
Conclusion
The work of W.C. Sabine founded the entire field of architectural acoustics and is fundamental to the successful interface of any electro-acoustic system to the acoustic environment. A partial list of present day equations directly based on Sabine's work are 1) critical distance, 2) reverberation, 3) reverberant sound field, 4) transmission loss, 5) Hopkins-Stryker and its many variations, 6) articulation loss of consonants, and 7) Q relative to the adjustment of direct-to-reverberant ratios.
The genius of the man is apparent, important, and yet relatively unheralded. Encyclopedias rarely mention him.
Outside of the field of architectural acoustics, students fail to recognize his name. Wallace Clement Sabine deserves our honored respect and acknowledgement.
Note on Symbols Used
The author is familiar with the symbols proposed for international use in the S.I. (called Systems International d'Unites by some and Systeme Idiotic by others) but prefers not to use them where their use is not mandatory.
Definition of Terms
V is the total internal volume of an enclosed space in ft3 or M3.
S is the total boundary surface area of an enclosed space in ft2 or M2.
a is the average absorption coefficient of an enclosed space (dimensionless),

s1,2,n, is the individual surface areas in the ft2 or M2 of the differing absorptive materials.
saobj is the total absorption figure for objects in the space that are not part of the boundary surface area.
RT60 is the time in seconds that it takes the steady state sound level in an enclosed space to drop 60 dB in level after the sound source is turned off.
D is the decay rate in dB/Sec of the steady state sound level after the sound source is shut off,
D = 60 / RT60
MFP is the mean free path in feet or M (i.e., the average distance the sound wave travels between encounters with boundaries, 4V M.F.P. = . S N is the total number of reflections during a given decay. For 60 dB of decay,
N = 6 In 10(1/a).
R.P.S. is the number of reflections per second,
R.P.S. = Velocity of sound / M.F.P.
Wa is the acoustic power in watts emitted by the sound source.
dB-PWL is the acoustic power in dB referred to 10-12W.
Q is the directivity factor of the sound source.

(Source: Audio magazine, Aug. 1978)
Also see: Another Look at Crossover Networks by Neville Thiele (Aug. 1978)
= = = =


