The perception of sound is a highly personal experience. It is neither art
nor science, but our own private view through one of the windows of the senses.
We can share that view through words and actions, so we know that others experience it also. But it is left for fools like myself to dare sift and quantify the ingredients of that experience in some hope of understanding what it is and how to make it more enjoyable.
I have wondered, as we all have, how we might be able one day to put numbers on the stuff of perception.
We are a long way from doing that. But in my own personal way I have been working on an allied problem. The problem of developing closer ties between what we measure in the physical world and what we seem to perceive of that same physical set of stimuli. I have come up with a few answers and I would like to share them with you. The results are applicable to audio analysis.
The technical details of what I am about to describe have been presented in a number of papers in the Journal of the Audio Engineering Society.
In this article, I want to present the reasoning behind the technical details.
The basic idea is extremely simple. If we write down the most commonly used words which we all use to describe what we hear, we find that there is a definite structure to those words. We can arrange the descriptive terminology into categories which are reminiscent of a geometric framework. The words have a gestalt basis and are linked to relationships in the totality of our sense experience, including vision, taste, and touch. I therefore suggest that we should use geometry to probe the interplay of these word concepts.
Here, I feel, is a link between subjective perception and objective analysis. Rather than use numbers, we should invoke form, texture, and the relationships among things. Model perception with gestalt, and use abstract geometry to analyze gestalt.
The term abstract, as I use it here, refers to the analysis of "things" which are not named and quantified in the general analysis, but which can be named and numbered when we are ready to do so.
I would like to state that my approach was greeted with great excitement. I would like to state it, but cannot. For one thing, the use of abstract analysis is in far left field, as far as most technical persons are concerned, if not outside the ball park altogether.
For another, the type of analysis that is required for even the simplest example in audio is pretty much uncharted. Among other things, we have to develop geometric tools for changing the dimensionality of an expression. And that's just for starters.
The Problem of Frequency
OK, where do we start if we want to apply the idea to audio? Well, I think the answer is easy. Start by cleaning up the mess we call frequency.
Let me state the problem. And in the statement I will give some of the answer. Then we can go on and develop the answer more fully.
The frequency description of a signal and the time description of that signal are tangled up with each other in a very fundamental way. The parameter that we call "time" and the parameter that we call "frequency" are not independent of each other.
And no amount of Band-Aid engineering with running transforms or things called instantaneous frequency is going to change that fact.
Yet in subjective audio, we know darn well there is the property of pitch which is frequency -like, and that pitch can change with relative time. So if we want to apply the existing high power mathematics of time domain and frequency domain to what we hear, we seem to need a joint frequency-time description. Ultimately, when we try that trick, we run into the fundamental relationship between time and frequency, a relationship which we ourselves created from the definitions we gave these things.
But rather than blame ourselves, we choose to imagine that nature has intervened and somehow, magically, put a limit on the precision with which a codetermination of these parameters can be established. We even give that a name, the uncertainty principle.
What leads us to this rather strange action is a very real need for some kind of math that has a time -like and a frequency -like (and a space-like, and so on) set of properties which can all be used in the same description. Up to now our tool box of math relationships has only contained the parameters related by Fourier transformation. So we've been stuck.
And by the way don't think that this is a problem unique to audio. Other disciplines face a similar dilemma.
But audio has a driving force which other disciplines do not. Audio has people who listen, and listening is what audio is all about, no matter how much chrome plate we use on our equipment. The listening experience implies not only that there are coexistent parameters, but there are more than just two of them.
==== Geometry Of Fourier Transformation ====
The appearance of anything depends upon the frame of reference we use to observe it. Geometrically, the Fourier transform is nothing more than a method of changing the frame of reference in such a way as to keep the number of dimensions the same but invert the units of measurement.
The Fourier transform is used in audio as the basis for converting time response to frequency response. In this case, the two frames of reference are one-dimensional. The unit of measurement of time is the second and the unit of measurement of frequency is the Hertz, which is an inverse time measurement.
This novel geometric approach to the meaning of Fourier transformation can be more readily visualized in a two-dimensional example, as shown in these figures. In this example, a two-dimensional system, shown with coordinates a and b, is a Fourier transformed version of the two-dimensional system with coordinates x and y.
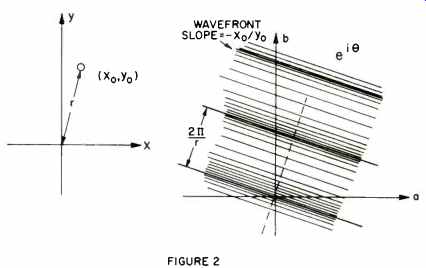
The requirement that the units of a-b and x-y be the inverse of each other shows up as the equation of a straight line, illustrated in Fig. 1. The parameter 0 acts to spread the value of any particular line passing through a point in x-y, say xo-yo, into a specific line in a-b.
The parameter theta thus acts as a spreading operator that doesn't govern "how much" but does govern "where." If we want to find out how the point xo-yo in system x-y appears to someone using the a-b system, we can pass a straight line through xo-y0 and rotate it like a propeller. This will sweep out all possible points in x-y, but only the common point xo-yo will build up to the highest possible contribution in the a-b system when we add everything up.
When we do that, we find that a point in the x-y system appears as the wave e^i theta in the a-b system. This is shown in Fig. 2.
The geometric requirement shows no partiality. The x-y system and the a-b system are duals of each other. So a point in a-b will appear as a wave in x-y.
The x-y system and a-b system are different ways of looking at the same thing. Each part of a thing as described in the x-y frame of reference will appear everywhere as waves to a person looking at it in the a-b frame of reference. That is not magic, but a result of the way we defined the a-b alternative view of x-y. If we say that something appears precisely at a single place along the x axis, we cannot then turn around and insist that it also be located at a precise position along the a axis.
Everything involving Fourier transformation must submit to this point wave duality. It makes no difference whether we started out defining things in terms of Fourier transformation, or discovered well along the road of other analysis that some of our parameters were Fourier transforms of each other. The fact remains that if Fourier transformation is involved, we will find that some of our parameters cannot be precisely codetermined.
When this happens, and when other experience tells us that such parameters should be co-determinable, or appear to be co-determinable under other conditions, then we probably made an improper identification. The parameters are not what we thought they were. That is true of what we call time and frequency, as well as some other mysterious victims of the uncertainty relation.
==== ==== ====== =====
History of the Term
So much for the problem. Now for a little bit of history. In 1862, Helmholtz completed one of the finest texts on music and sound ever written. Highly successful, "On the Sensations of Tone as a Physiological Basis for the Theory of Music" was translated into English in 1885 and remains, even today, one of the finest discussions of the topic. It is still in print. To my knowledge, this is one of the first books to use Fourier series as a basis for analyzing complicated periodic signals.
The English translation used the phrase "vibration number" in the first edition to identify the number of vibrations a sound completes in a fixed period of time. The second edition changed that to "pitch number" so as to align it with the sensation of pitch as a numerical quantity. Fourier series were stated in terms of pitch number.
The pitch number was also called "frequency" by the translator in that second edition, "...as it is much used by acousticians...". Prior to that translation, 100 years ago in 1877, Rayleigh completed volume one of his equally famous The Theory of Sound. Two giant contributions to the knowledge of sound.
Helmholtz preceded Rayleigh like a flash of lightning precedes the roll of thunder.
Rayleigh also needed a word to denote the number of vibrations executed in a unit of time. So Rayleigh called it frequency, stating that this word had been used for this purpose by Young and Everett. It is clear that Rayleigh equated the concepts of pitch and frequency, at least on a numerical scale.
Thus, while Helmholtz only used the term pitch number, his translator introduced the terminology "frequency". And since the translation occurred after the publication of Rayleigh's The Theory of Sound (which cited Helmholtz' German text in a number of places), it is possible that it was Rayleigh who really got this word started as applied to sound.
So what's wrong? Isn't it possible for a tone to change pitch with time? Of course, pitch can change with relative time. But frequency cannot! The Fourier Transform
Now, let's do a wild thing. Let's use geometry to derive the mathematical relationship known as the Fourier transform. Then, from this geometric base, let's determine what the word "frequency" really means. And you won't find this in text books, at least not yet.
Let us begin to look at things geometrically. Suppose we want to measure something. How do we start?
In my opinion, the best advice on this matter was given by Albert Einstein who said, "It is the theory which decides what we can observe." For one thing, it is the theory that determines the frame of reference we are going to use for the observation. A typical frame of reference for audio measurements is the passage of time, measured in seconds.
Having established this frame of reference we can set up instruments responsive in that system. An oscilloscope might be considered such an instrument. So we make oscilloscope measurements.
This next step is a big one. There is an infinity of frames of reference we can use. Each frame of reference is complete in itself and is a legitimate alternative for the description of an event. I call that the Principle of Alternatives.
If the passage of time is a legitimate frame of reference, then it is only one of an infinite number of alternatives.
What might we be able to say about some of these alternatives? In order to answer that, we need to take an even bigger mental step. We need to accept the fact that the alternatives may differ in the number of dimensions as well as the way in which the units are measured.
Dimension? Yes. Consider the conventional waveform presentation of the signal coming out of an amplifier, volts as a function of time. Time in this sense generates what is geometrically called a "one-dimensional manifold." Each place in the dimension of time has a signal value associated with it.
The distance between two places in time is measured in units we call seconds.
Suppose we want to change our frame of reference to come up with some alternate system of measurement. There are rules for changing the form of presentation from one frame of reference to another. The process of doing this is called a transformation.
If we transform in such a way that we do not change the number of dimensions, but have a new reference system measured in units which are the inverse of what we came from, then this very special transform is called the Fourier transformation. So it should be possible to transform our one-dimensional time measurement into a one-dimensional thing measured in inverse time, somethings per second. If we perform a measurement in this new frame of reference, we will call it the frequency response measured in Hertz.
For those who feel I am trying to pull the wool over their eyes, let us now actually derive the mathematical expression of the Fourier transform from these first principles of geometry.
I like to use pictures, so let me show how to derive the equation from considering the problem for some two-dimensional frame of reference.
In Fig. 1 let us assume we have a two-dimensional coordinate system, shown as x and y. This two-dimensional frame of reference is complete in characterizing something of importance. For example, it may be the reference system for a photograph with the distance between coordinate points measured in units of millimeters.
The Fourier transform of this will be another two-dimensional system in which the distance between two points corresponds to inverse millimeters. This is the a-b system.
The question is, how do we go from x-y to a-b? We know the units are such that their product is a "dimensionless" value. (Millimeters times constant per millimeter is constant.) So let us say that the axis x will bear a special relationship to the axis a such that if we mark off some distance along x we will find that the thing that happens along a is a corresponding distance such that, x a = constant.
And the same thing will happen between y and b.
What we have required is that the relationship between x-y and a-b be dimensionally reciprocal such that, 0 = ax + by
The Greek letter theta Θ stands for a fixed number, and it can be any number we choose it to be. I use the symbol Θ because we are going to make that equal to the angle of something.
Look at this equation as some geometric curve in the x-y system. This is the equation of a straight line. The coefficients a and b in that equation determine the angle which the straight line makes with the x-y axes, and the constant o determines where the line cuts across the axes.
There is a deep geometric significance to this relationship. The need for not changing dimension, but inverting measurements, leads to a zero curvature surface having one less dimension than the space in which it is imbedded. In two dimensions, this is a straight line. In one dimension, it is a point, and in three dimensions, it is a plane. Since most of our geometric thinking is done in three dimensions, this type of surface is called a plane when we are in three dimensions, and a hyperplane when we are in other dimensions. A straight line is a hyperplane in a two-dimensional system.
The general equation of a hyperplane is always the sum of products of coefficients and coordinates as we have written down. In three dimensions, there are three terms equal to Θ. In one dimension, there is only one term equal to Θ. When we are comfortably seated in any frame of reference, the way we see the coordinate axes of the alternate Fourier transform view is as coefficients of hyperplane surfaces passing through our space. After all, the Fourier -transformed view is another way of looking at the same thing we observe, so we should be able to see the structure of the other frame of reference as something in our view.
Now, let's go back to our two-dimensional example and ask how we could take any place in the x-y system, xo-yo for example, and find out how it is distributed in the a-b reference system.
The relationship is in terms of straight lines (hyperplanes) passing through xo-yo. Each line passing through xo-yo tells what a and b coordinate locations will contain the information of all x and y values along that line. A neat thing happens. No matter what the angle the line makes in the x-y system as it passes through xo-yo, the result will be a straight line in the a-b system which has a constant slope.
If we want to find out how xo-yo (and only xo-yo) appears in the a-b system, there is only one thing we can do to the straight lines passing through xo-yo-we can rotate them around xo yo like a propeller about its shaft. And that's where we find the angle Θ. We take the value of the signal at the point x-y and multiply it times the angle of all lines passing through that point to find out how that point is smeared over the a-b system.
The mathematical expression for this is, ei Θ If we write that out and see what it corresponds to in the a-b system, we find a startling fact. Each point in the x-y system is represented by a wave uniform over the whole of the a-b system. The period of this wave is the reciprocal of the distance from the point to its origin, and the angle of the wave in the a-b system is such that the wavefront is perpendicular to the angle the original point has with respect to its x-y axes. This is shown in Fig. 2.
I hope this rings a few bells, if not setting off sirens. The geometric relationship inherent in Fourier transformation is such that a point (particle) in one frame of reference will be manifest as a wave in the alternate frame of reference, and conversely.
Therefore (underline, exclamation point, big arrow), Fourier transformation is a local-to-global map, in which each point in one becomes everywhere in the other.
Now suppose we try a dumb-dumb and attempt to describe the same thing in terms of the x-y and the a-b system. Here is what happens. We can codetermine the location of a point in x and y, or in a and b, or along x and along b, or along y and along a. But we are going to run smack up against our own definition if we attempt codetermination along x and a or along y and b. Not because nature stepped in and pulled a curtain over our results. But because we are trying to violate the very conditions we set down to derive this particular transformation.
What form will that codetermination be stymied at? The form is determined by the equation of the hyperplane (which is another way of saying the equation of a wave) and is, Ax Da >_ number äy äb >_ number where the triangle means the extent of the range of parameter where most of the value of the same thing is concentrated.
Oh yes, the equation of the Fourier transformation.
We add up the contributions of each point in x and y, which is called integration. In two dimensions this becomes, g (a, b) = fff(x,y) eie dx-dy
If you're not into math, don't worry about this equation. The equation is not important. The ideas that led us to the equations are what are important.
And the principal idea, that can never be repeated too often, is that expressions joined by transformation are nothing more than different ways of describing the same thing.
The Meaning of Frequency Now!
What the devil does frequency mean? Frequency and time are alternate coordinate systems for describing the same thing. Frequency cannot change with time because frequency and time are different ways of describing the same thing.
In our haste to match sense experience with some existing mathematics, we have found a thing called frequency which has a pitch -like behavior, and we found another thing which has a time -like behavior and we use them. The greatest majority of the cases we encounter in audio have number values such that the interrelationship between frequency and this time -like parameter does not cause any trouble. And that is a soporific because we have lulled ourselves into the belief that there could not be anything else needed, or available, to handle any problem.
The concept of harmony, the agreeable combination of sounds, got its first mathematical treatment in the days of ancient Greece when the Pythagoreans observed certain numerical relationships in musical sounds.
Two equally taut plucked strings harmonize only when their lengths are in certain ratios to each other. The musical intervals of unison, octave, fourth, and fifth are related to the numbers 1, 2, 3, and 4.
When Helmholtz and Rayleigh analyzed sound, they did so in an age-old frame of reference that tied sound to the passage of time. Fourier's theorem that any repetitive function could be generated by proper combination of sine waves, the shape of the purest tones in music, made everything fall into place. Nothing could be more natural than to use this mathematics for the analysis of complex sounds.
I do not believe that either Helmholtz or Rayleigh had visions of replacing the parameter of time with frequency. Frequency was a convenient expression that made a lot of sense in the analysis of tones.
Helmholtz and Rayleigh, and almost everyone after them, used some ready-made mathematics as a model that fit perception pretty well. We experience a thing we call time. We give it a symbol, t, and write equations using t. Juggling the equations produces a new parameter, which we call frequency. If we do not look too hard, this parameter called frequency seems to behave analogous to another thing we perceive, which we call pitch.
Here is the catch. The parameter t is not the time of our perception. Nor is the parameter w the pitch of our perception. t and w are mathematical entities that are different versions of each other. The theory decides the observation. If we set up an observation in the parameter t, we will get measurements in the parameter t. We can transform the mathematics in t to a mathematics in w. If we set up observations in the parameter w, we will get measurements in the parameter w.
We can transform the mathematics in t to a mathematics using four parameters if we choose. And if we set up observations in those four parameters we will get measurements in those four parameters. That is the significance of the Principle of Alternatives.
The fact that we can break out of the t -to -w -to -t loop, which we call Fourier transform, is what is brand new in this theory.
It happens that the representations in t and the representations in w do a pretty good job of modeling most of the things we need to analyze in audio. There are higher -dimensional versions of the t and w representation, an infinity of them. Some of these versions have coexistent time-like and pitch-like parameters. The difference between the representation of a signal using these higher -dimensional parameters and what we get from gluing together a t and an w axis to pretend we have higher -dimensionality is lost in the noise for most of what we do. For that reason, we might as well continue using the impulse response and steady state frequency response for loudspeakers, amplifiers, and the like. After all, the impulse response and the frequency response do have a meaning and they are legitimate measurements. It just happens that in detail the meaning is not what we thought it was.
But where we need to recognize the limitations of t and w representations is when we get involved in the interpretation of these measurements with perception, which has a higher dimensionality. It is then that the geometry is important.
Let me put this another way. You out there, Golden Ears, the person who couldn't care less about present technical measurements but thinks of sound in gestalt terms as a holistic experience. You're right, you know.
(adapted from Audio magazine, June 1977)
Also see:
Listening and Experience (Aug. 1992)
= = = =