
By PAUL ASMUS /Application Engineer, Calculator Products Div., Hewlett-Packard Co.
The author compares the desk-top programmable calculator as an engineering tool with mini and time-sharing types and explains why such calculators have a unique role to fulfill.
Editor's Note: We have scheduled for next month an article covering "minicomputers" by Rob Katz of Digital Equipment Co. and, in the following issue, we hope to bring you the "case "for time-sharing, as presented by Lee N. Beyer of General Electric.
THERE seems to be a new gap in the engineering and scientific community. In fact, it fs a yawning chasm. Call it the computing gap. On one side of the gap is a computer with its awesome power; on the other side is the slide rule, adding machine, pencil, and you . . . with a fist full of problems. If you are an engineer, scientist, technician-if you are engaged in any type of technical work, a large part of your job involves calculating. There are design calculations to make, reports to prepare, and things to analyze. How many of those particular components should be stocked? What would happen if we moved the center frequency down to 21 kHz? What's the mean time between failure for those modules? How many of those parts do we have to test to be sure they are going to meet a certain spec? And the list goes on.


-- Users of programmable calculators interact more closely with their
calculations and gain knowledge in the process.
-- Programmable calculators are approachable, powerful, and easy to use. Various input and output peripherals are also available.
Some problems are a perfect match for a computer; they are big; they are unwieldy; they require lots of data; and they don't require much human interaction. Quite a few problems can be done in your head or just scratched out in 20 seconds on a piece of paper. But an uncomfortably large percentage of calculations that have to be made fall right in the middle of the computing gap. Some of them are too small to put on a computer, but too big to do in your head or on a slide rule. Some are things you never really decided how best to handle, or things that had to be done by a certain time but couldn't be processed through the system soon enough. All are things that, for one reason or another, did not fit the computer and just couldn't be done by hand. As a result of their falling into the gap, many of these problems never get solved to your satisfaction. They get worked out one way or another-maybe you guess that a 10% resistor would do. A "wet finger in the wind" told you that if you tested five of them, the rest would be OK. You never knew for sure. You never got that answer you wanted. Some of these problems may still be around.
Bridging the Gap
The programmable calculator bridges the computer gap because it's approachable and personal: approachable because it is easy to use--almost self-explanatory, and personal because it's flexible enough to be tailored to your requirements. You set it up to do what you need in the way you need it done. And even though it is as approachable as your slide rule, it still has much of the calculating power of a big computer.
Inside, the programmable calculator is really a small computer: it has a memory, it has control, input-output elements, it stores data, and it can be programmed. On the outside it's quite different. It is small-about the size of a typewriter-and has a keyboard and display. The display is numerical, showing answers and interim results. Most calculators display the contents of two or three registers where calculations are done.
The keyboard is an "English language" one, much like that of an adding machine. Parts of it actually operate like an adding machine. There is a plus key for adding, a minus key for subtracting; there are keys for finding square roots or even cosines. When a key is pressed, the result is displayed immediately. The keyboards of most programmable calculators are divided into four main functional groups: the arithmetic group, storage group, special-function group, and programming group.
Somewhere near the center of the keyboard will be the arithmetic group. This group facilitates number entry and includes all arithmetic operations: add, subtract, multiply, divide, and square root. Numbers can be entered either in decimal or scientific notation (powers of 10). Most programmable calculators display at least 10 digits. Numbers entered can be displayed either in scientific notation or in straightforward decimal notation, with as many decimal places as the user needs. Although the machine always calculates its answers to 12 places, you can have the answer displayed with only two-place accuracy and it will even round the answer for you.
The second group of keys, usually located in close proximity to the arithmetic group, is for storage and manipulation. These keys control storage and exchange of numbers between display and storage. Numbers storage is easy--simply press a storage instruction key and the key corresponding to the desired storage location, and the number is stored. To get the number back, press the recall instruction key and the key corresponding to the storage location.
Sometimes recall is done with a single key stroke. For example, in the keyboard shown in the photograph, to store the contents of the X-display register in the register called "d." one simply presses the keystroke sequence: `:x-.( )," "d" (called "x to" d). To recall that number, the "d" key is pressed.
The third group, which gives the unit extra calculating power, is a special-function group. The special-function group includes commonly used mathematical functions, such as trig functions, logs, square roots, and exponentials.
Often these keys include such functions as rectangular-to-polar conversion or single key-stroke summations. All functions are represented by a single key; to find the sine of a number, simply enter the number via the arithmetic keyboard and press the sine key.
Given the first three blocks of keys, the calculator becomes an electronic slide rule, combining the best features of an adding machine, a slide rule, and a book of tables.
Expressions like e = EF (1-e- °/RC), the voltage on a capacitor, can be determined in seconds with just a few operations. No special training is required-only an understanding of what each key does. Most programmable calculators have a pull-out card which explains what each key does and gives examples of how the keys work. It is possible for a person totally unfamiliar with a calculator to do a fairly complicated problem on the calculator the very first time he tries. As a matter of fact, this has been the experience of many calculator users.
The fourth and final key block is for programming. This set of keys controls the program mode of the calculator and defines certain functions necessary for programming: such as starting a program, stopping a program, taking data from input devices or sending data to a peripheral, branching to a different part of a program, making a decision, etc. Calculator programs are written by switching the calculator to a "program" or "learn" mode; pressing the keys corresponding to the desired operation in the same sequence that would have been used to do the calculation manually; and then switching back to the "run" mode. Several keys in the programming keyboard must be used at the beginning of the program and at various points in the program, in addition to the keys needed to do the calculation manually.
Anyone who can do a calculation manually can write a program for his calculation. The transition from machine operation to machine programming is an easy one. Most people can learn to program a calculator in less than one working day and become proficient calculator programmers in a few days.

-- The calculator keyboard and display--the "heart" of
8 personal computing system.
Besides being approachable, easy to use, and easy to program, programmable calculators are powerful and accurate, with accuracies generally on the order of one part in a trillion and dynamic ranges large enough to simultaneously handle numbers as small as 10-98 and as large as 10". Handling picofarads and megohms in the same expression is no problem. Most programmable calculators can handle programs varying in length from about 200 program steps for a basic machine to about 3500 steps for a fully expanded machine, where each program step represents one keyboard key-stroke. Basic calculators with memories in the 200 to 500 program-step range can handle various problems including statistics, electrical engineering, solutions to four simultaneous equations, amplifier gain and phase calculations, simple filter designs, conversions from S-parameters to other parameters, and so on.
A good example is an RC timing or trigger-circuit design program written by one user. This program can calculate either capacitor value, resistor value, critical voltage, or delay time. Given any three values, the calculator finds the fourth. Then the program allows the operator to change any of the four values and note the effect on any of the other three. For example, he can change the resistor from the calculated value to the next closest standard value and note the effect on delay time; or can change capacitance value in a similar way; or vary the resistance value 10% to see how resistor tolerance will affect delay time. This isn't a complicated calculation, but does involve manipulation of exponential functions. It could be done on a slide rule or with a book of tables, but on the calculator it is done more quickly.
And it allows the engineer to optimize the circuit instead of just design it, probably in less time than it would have taken him to do one calculation by hand. Here we have a problem too small for a computer and just a bit too complex to do by hand-one that probably wouldn't get done without a calculator.
A fully expanded calculator, one with 3000 to 4000 steps, almost rivals a small computer in capability. Such a calculator can do a problem like an RCL network analysis with 15 nodes and as many as 45 components, and plot results on a Smith chart or log paper; or could fit a 12th order curve to a set of data points; or invert a 14 X 14 matrix. Although such a calculator, fully expanded, virtually matches a small computer in capability, it still is as easy to use as a basic calculator.
Inputs and Outputs
There is more to a problem than just getting an answer; there's the matter of getting results in a usable form. Basic calculators can be expanded to include a wide variety of peripherals to generate outputs and accept inputs in about any form the user desires. There are printers, fast, quiet, reliable, and inexpensive; there are typewriters and teletypewriters for fully formatted outputs, for filling out forms and reports; there are X-Y plotters to help provide the invaluable insight that only plots and graphs can give; there are tape readers, card readers, and interfaces to measuring instruments; and there are large-screen displays, memory extenders, and even a new peripheral called the "Digitizer" that allows graphical data from a plotter or hand-drawn graphs to be entered into the calculator. The calculator system can be configured to meet almost any requirement and then later expanded and modified to meet different requirements. Get a calculator now; as your work load increases replace the printer with a typewriter and keep the printer for smaller jobs, or add a plotter. As the need for larger programs arises, expand the memory to handle them. A fully expanded system with all the peripherals is still just as approachable as your slide rule.
More than a Calculator
Calculators offer much more than just solutions to problems. They make better engineers and technicians by helping them make better decisions. They help people learn about computing, about computers, about mathematics and programming, and more about the work they are doing.
For example, the programmable calculator encourages people to do things they might not otherwise tackle. A perfect example of this is the RC timing circuit program mentioned earlier. Here is a problem that might not have been solved without a calculator. But, because the calculator was so easy to program, maybe even fun to program, someone wrote a program to solve a simple but persistent problem that had been around for a while. And it turned out to be quite valuable. This will, in turn, encourage an engineer to try other things--maybe, "I haven't time to mess with that" will be replaced by, "Let's try that on the calculator." A programmable calculator can also stimulate new awareness and insight. Since the calculator is so easy to use and program, it is possible to interact more closely with the problem. Freed from the leg-work of setting up the problem, users have time to take a closer look at what they are doing. Consider, for example, an engineer designing an antenna. One of the tools he uses is a pattern plot or plot of field-strength versus direction. Although calculations involved in making such a plot are not especially difficult, they are often messy and time consuming; nothing really unusual in them, but lots of sines and cosines to look up and lots of things to jot down. A plot program is easily prepared for a programmable calculator, especially one with built-in trig and single-step rectangular-to-polar conversion functions. With the calculator and a peripheral plotter, a finished plot is ready in less time than it would have taken to calculate one point by hand. So, instead of making just one plot, the designer decides to change a couple of variables and make another plot; in fact, several plots-he changes the number of turns of this and terminations of that, or length of the other. Pretty soon he starts to notice things; that back lobe which wouldn't meet Federal specifications alternately widens and narrows as he varies the length of one of the elements; or those pesky side lobes start to disappear as the number of turns exceeds a certain figure. He's gaining insight into what antennas are all about. Next time he designs an antenna, he'll know more about it because he learned while doing calculations.
There are other benefits, too; for example, having calculator power available when you need it, as in lab situations where it is important to process data as soon as it appears or when a production facility must be shut down while someone decides on a course of action. Also, people who have never used computers or calculators before will be encouraged to try their hand on a programmable calculator.
Then, there is the matter of cost. A programmable calculator system can be put to work for less than $1 per computing hour. One survey conducted by Hewlett-Packard indicated that its customers feel that an average of 58 percent of all the calculating they had to do could be done on their programmable calculators; while 16 percent reported that 90 percent of their work could be handled on a programmable calculator. The basic calculator system costs less than $4000 but can be enlarged to a fully expanded system with all peripherals for an additional $10,000. The most expensive calculator system one can configure would cost less than $20,000 and rival a small computer in capability. A calculator system which would meet the needs of most people would cost about $5000.
What About Mini and Time-Share Computers?
In general, it can be said that calculators make poor computers and computers make poor calculators. That is to say nothing derogatory about either computers or calculators but rather to point out that they aren't really competitive.
One does not use a calculator instead of a computer and vice versa. Each is designed to handle a specific job and are complementary.
Calculators are useful for those jobs that fall in the gap--jobs that don't get done now, jobs that need your personal attention, and ones no one seems to have time to do. Calculators are designed to help people interact with their problems. Computers-big computers, small computers, and time share-have wider scope; they can perform more complicated calculations in much less time-often for a great deal more money. They can accommodate many users and many different languages. They are general-purpose machines, intended for no specific kind of problem; but capable, after some programming, of handling about any task.
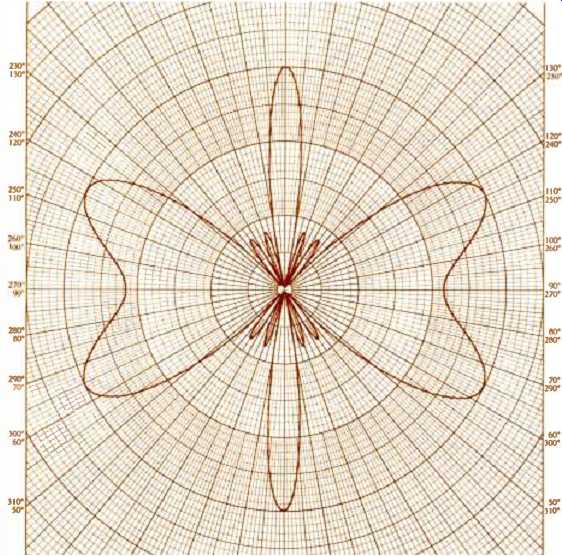
--- A broadside array antenna plot made by a programmable calculator.
Automatic plotting facilitates new design development.
But the more general the device, the more one must know about it in order-to use it profitably. There is no way of looking at a computer and telling what it is doing, where its answers are, or even what programming language it is using. One doesn't just walk up to a computer and ask what (1-e06) is. One doesn't look at a computer or time-share terminal and get the answers; the user must program it to present the answers on one of the many output devices.
But, once a person understands how to use the computer, he has almost unlimited computing power.
If a computer is to be utilized effectively, it must serve many people, and so must be administered. Anything an intended user wishes to do must pass, to some extent, through that administration. One doesn't just walk up and grab a computer. Thus a computer is less approachable than a calculator, and necessarily so.
Organizations faced with a wide variety of problems find that a combination of calculators and computers gives them the best return for their computing dollar and best utilization of their people. This way there is something for everyone; calculators aren't overtaxed to the point where they become inefficient and computers aren't tied up doing simple problems. They also find that computer familiarization is easier and that people who learn about calculators and computers have a better understanding of each.
How Do You Pick a Calculator?
The best answer-considering a calculator as a personal computing system-is to select a calculator which you, the user, feel will best handle your requirements and your problems. Since programmable calculators are a relatively new product, there is disagreement as to what constitutes the "best" calculator. Some say it's the one with the most program steps; others say the one with the most built-in functions; still others insist it is the one that weighs the least, or has the most peripherals. If it were only a matter of program steps, then the best choice wouldn't even be a calculator, since there are many computing-equipment devices that have more program steps than the biggest calculator. If it were a matter of weight, a slide rule would win. It is not inconceivable that you might even consider the calculator's portability if you need it away from your office. Some engineers are known to take their calculators along with them on business trips.
Remember, the programmable calculator was designed to be a personal, interactive computing system to help you solve problems the way you want them solved. So, your calculator must be easy to use, easy to understand, easy to program, and flexible enough to meet your changing needs. Perhaps the best way to choose a programmable calculator is to try several and choose the one that best fits the way you plan to use it. Try it out on one of your problems to see how easy it is to program. After all, it is to be your personal computing system.
Programmable calculators have helped close the computing gap. Now there is a calculating tool for almost every kind of problem. The trend in calculators will most certainly be towards smaller units, with greater capability, that are even easier to use and easier to program-probably at lower prices.
There will be more peripherals and they will be more flexible. Advances in electronics technology will make possible large amounts of calculating capability in a box no larger than a typewriter, yet still be as approachable as your slide rule.
======
Reliable Electronic Intrusion Alarm
======
(adapted from: Electronics World magazine; Jul. 1975)
================