
The Overselling of Oversampling. The truth behind
digital filters in CD players. by DAVID RANADA
Digital Output Filters in CD Players Have Been Misleadingly Over-promoted.
BY DAVID RANADA
NO single component feature in the recent history of audio has been the subject of so much hyperbole as the oversampling digital output filters used in Compact Disc players and other digital-audio devices.
Although they were originally introduced to make up for the unwillingness, or inability, of a certain manufacturer to make 16-bit digital-to-analog converter (DAC) chips, it now seems that digital output filters are absolutely de rigueur in any new CD player. Even well-read and conscientious audiophiles believe that the higher the oversampling rate, the bet ter. These attitudes grow out of CD-player ads and promotional materials that are misleading in content and presentation. But before I get to the pictures that aren't worth a thousand words, the answer to a fundamental question: Why output filters? Any digital-audio component that converts data into an audio signal also simultaneously produces in that signal a host of ultra sonic "images." As shown in Figure la, a sampled audio signal, such as that contained on a CD, when directly reproduced by a DAC contains not only the baseband audio signal, extending up to 20 kHz (tinted area), but also images of the signal centered around multiples of the original sampling frequency. These spectral images are responsible for the evenly stepped appearance of a digital-audio signal along an oscilloscope's horizontal time axis (Fig. 2a). (The vertically stepped appearance results from quantization and is a separate issue.) Theoretically, the images extend infinitely upward in frequency, but, for a variety of reasons, their level eventually rolls off in practice. The purpose of a digital or analog output filter is to suppress the high-frequency images.
But the images are all above 20 kHz and are thus ultrasonic- they are, therefore, inaudible. The truth is, you don't even need output filters. You could feed a converted digital-audio signal directly from a DAC into a stereo system-images and all-and if it were accurately reproduced by that system, it would sound fine: You would hear music just as if the filter were present. (Actually, a little filtering might be necessary to provide a baseband-response-flattening "aperture correction.") However, to quote the Philips Technical Review (Vol. 40, No. 6): "Even though the frequencies above 20 kHz are inaudible, they would overload the amplifier and set up intermodulation products with the baseband frequencies or possibly with the high-frequency bias current of a[n analog] tape recorder. Therefore all signals at frequencies above the baseband should be attenuated by at least 50 dB." The called-for attenuation can be achieved in only one way: a sharp cutoff low-pass (high-cut) filter. (The concern expressed over taping is interesting. Philips, which has been of late working on various anti-taping systems for DAT, seems to have considered dubbing a legitimate activity, at least back in 1982.)
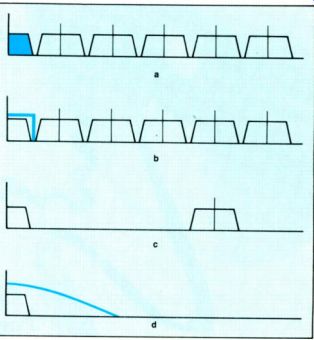
Figure 1. A 44.1-kHz DAC output spectrum (a). in addition to baseband audio information (color). contains ultrasonic images that have to be eliminated by filtering. Either an analog (b) or digital (c) filter can be used. Most digitally filtered CD players have a supplementary, slow rolloff analog filter (d) that attenuates any remaining images.
----------------
Are filter phase shifts audible?
Judging by the constant attention given the subject in CD player advertising and other uninformed commentary, various attempts by this magazine and others to quell the continuing exaggeration of the importance of high-frequency phase response have obviously failed. Nonetheless, I'll try again.
Stated as simply as possible, the amount of phase nonlinearity introduced by a typical analog CD-player low-pass filter is inaudible. Analog low-pass filters may indeed have some audible problems (such as slight ripples in frequency response), but phase nonlinearity is not one of them. This has been well established since at least 1984. In "Perception of Phase Distortion in Anti-Alias Filters," published in the November issue of Journal of the Audio Engineering Society for that year, Douglas Preis and P. J. Bloom report the results of tests for audible differences between linear-phase filters and "minimum-phase" steep-rolloff filters (which are, for purpose of this article, identical to analog CD-player output filters) of equivalent frequency response. They found that a cascade of eight identical 15-kHz low-pass filters "introduced no perceptible effects." You get only one of these filters per channel in a CD player, and its turnover frequency is an even more difficult-to-hear 20 kHz or higher.
Still not satisfied? Psychoacoustical experiments have shown, well before the Preis/Bloom tests, that the ear is insensitive to group delays (differential phase shifts according to frequency, measured in seconds rather than degrees) of less than about five to ten milliseconds at the higher audible frequencies. Therefore, at a CD-player output-filter frequency of 20 kHz, an analog filter could have five milliseconds of group delay-equivalent to 36,000 degrees of phase shift (!)--before that phase nonlinearity could approach audible thresholds.
This is far more phase shift than is produced by any reasonable analog output filter: An eleventh-order, 20-kHz analog filter would generate at most only 1,980 degrees of phase shift (0.275 milliseconds of group delay), and that happens only very near the cutoff frequency. The eight series-connected filters in the Preis/Bloom tests had a total maximum group de lay of between five and six milliseconds.
There are biological reasons for the ear's insensitivity to phase effects at high frequencies. A nerve cell, such as those found in sound-transducing portions of the inner ear, can "fire" electrochemical impulses no faster than about once per millisecond. At 20 kHz, one millisecond is 20 cycles (7,200 degrees) of phase shift. The brain itself has to see a few neuron firings before it realizes something is happening. That will produce several more thousand degrees of allowable phase shift at 20 kHz.
To sense a group delay on a single audio channel, the brain has to compare sound arrivals of different portions of the audible spectrum. Although the brain does have the required net work to look across the entire spectral-data output of the ear simultaneously, it is composed of many nerve cells, each one of which contributes its own share of timing "slop" to the pro cess. Simply because of the way it is wired, the brain is not good at detecting small intra-channel group delays. Interchannel phase shifts (below about 1.5 kHz) are used extensively by the ear/brain system to determine sound-source location, and the nerve-cell pathways between the two ears and the inter aural-comparison area of the brain are, accordingly, extremely simple and rapid. So we are relatively sensitive to phase shifts between stereo channels (when they occur at low or middle frequencies), but not to phase shifts within one channel.
The argument so far has ignored the properties of music signals. So what if the ear/brain system could hear the relatively slight phase shifts at 20 kHz introduced by an analog output filter? Is there anything up there to get phase-shifted in the first place? Not much. At the extreme top of the audio spectrum, typical music signals have levels at least 20 dB be low the maximum-level region around 500 Hz, and lower-frequency information usually will mask any phase anomalies at the high end.
All of the preceding assumes that one is actually capable of hearing frequencies up near 20 kHz. But the typical reader of this magazine cannot, because his high-frequency hearing has already deteriorated, rather early in life. If you can't hear the horizontal scanning frequency generated when you turn on your TV, then either your TV's horizontal flyback transformer has an atypically low acoustical output or you have lost the ability to hear 15.734 kHz and above-in which case you can even more blissfully ignore any and all references to the presence or absence of CD-player output-filter phase shifts.
D.R.
------------------------
Why a digital filter?
The filters used in all first-generation CD players--except those units originating from Philips--were analog. They used resistors, capacitors, inductors, and op-amps to achieve the required "brick wall" response characteristic: as flat as possible up to a certain frequency (20 kHz) and then plummeting downward in a very steep rolloff, as if the frequency-response curve had hit a brick wall (Fig. 1b). Such analog filters can have problems. Either the many parts in each filter must be carefully chosen, or they have to be trimmed for best response. The circuit elements can drift in value, as can the trimmer settings, throwing off the filter's behavior. Analog filters can be noisy and can suffer from sub-stage overload, but, correctly designed and built, an analog output filter can also be audibly benign. Noise can be made lower than the minimum CD noise level; frequency-response ripples and distortion can be reduced to inaudibly low values; and filter characteristics can be made stable by judicious choice of parts. The phase nonlinearity introduced by analog output filters has never been an audible problem (see "Are filter phase shifts audible?", p. 62). Philips went its own way back in 1982. The first Philips CD players used a digital filter, which performs mathematical manipulations on the audio while it is still in digital form. It is instructive to examine Philips's rationale for using a digital filter.
The 1982 Philips Technical Review article continues: "An analog filter after the digital-to-analog converter will inevitably have to contain a large number of elements and require trimming. In addition, a linear phase characteristic is required in the passband so that the waveform of pulsed sound effects will not be impaired [italics added]." Note the nascent fixation-now fully developed by many CD-player manufacturers but, ironically and thankfully, still rather muted at Philips--on preserving the shape of the audio signal (its waveform), not on any audible factors.
The first Philips CD-player digital filter was a four-times oversampling device; that is, it used data processing to attenuate all the ultrasonic images between the baseband and the one centered around 176.4 kHz (four times the sampling rate). Remember that the images are a result of the original 44.1-kHz sampling process and are present in the data on a CD. A digital filter, since it essentially re-samples the original data at a higher rate, also generates images, but these are spaced farther apart, according to the re sampling (oversampling) rate (Fig. 1c, showing the effect of a four-times resampling filter). The "space" created by the spreading of spectral images from a digital filter permits the use of a slow-rolloff, low-phase-shift analog filter to remove the remaining images (Fig. 1d). Philips originally used a third-order Bessel filter with a -3-dB point at 30 kHz. The company explained: "The Bessel type of filter has been selected because of its linear phase characteristic in the passband. This filter is simple and requires no highly accurate elements."
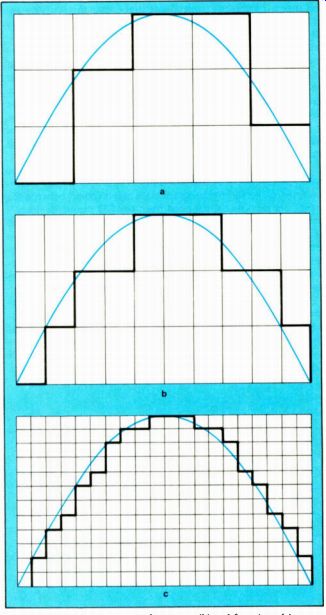
Figure 2. Although the outputs of two-times (b) and four-times (c)
over sampled digital filters look closer to the original waveform (color),
analog filtering of 44.1-kHz samples (a) will also produce a smooth
curve.
That last sentence points to one of the most important reasons Philips used digital filters and why other manufacturers are switching to them: They can make a CD player less expensive to produce by simplifying the design and part-quality requirements of the remaining analog output filter. (The first Philips digital filter contained processing that even enabled the use of 14-bit DACs, as opposed to more expensive 16-bit units.) And since, by now, digital filters are perceived by the consumer-rightly or wrongly-as a definite plus, more CD players will be sold. Profit! It is difficult not to fall into a disgusted cynicism here. But the ads, product brochures, and engineering white papers keep coming out with the same tired figures and diagrams in support of "higher resolution" digital filters and ever-increasing oversampling rates. I can't help wondering whether such free use of hyperbole will not eventually dilute the impact and lessen the influence of truly legitimate, audibly significant product claims and engineering developments. Meanwhile, gauge for yourself whether the familiar digital-filter claims are valid.
What's wrong with these pictures?
Figure 2 purportedly shows how two-times oversampling (b) is closer to the original curved, analog waveform (in color) than regular 44.1-kHz sampling (a), and how 18-bit, four-times oversampling gets even closer (c). One could continue in this vein, using eight-, 16-, 32-, 64-, and 128-times (etc.) oversampling, with increasingly good-looking stairstep waveforms each time. But re call that the sampling by-products that create the stairstep appearance of these waveforms in the first place are entirely ultrasonic. Remove the ultrasonics--by digital or analog filters--and all these waveforms will revert to the same graceful analog curve. Don't remove the ultrasonics, and your ears will still hear that analog curve, as long as the spurious signals don't distort or inter-modulate in the rest of your audio system. On the other hand, the added amplitude (vertical) resolution provided by the 18-bit conversion in Figure 2c may be beneficial insofar as it helps assure linear, low-distortion decoding of low-level information, even though it cannot get more out of a CD than was recorded onto it (see my "Golden Rulers," May).
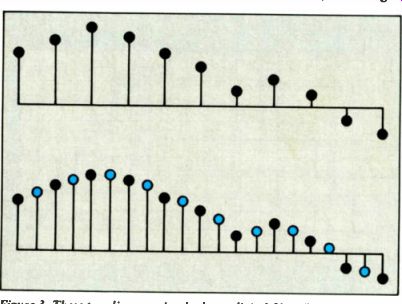
Figure 3. These two diagrams imply that a digital filter (bottom)
simply fills in the gaps between the original samples (top), but practical
design limitations may force even the original samples to be slightly
altered.
There is more. Figure 3 shows how digital filters operate in the time domain. In effect, the two-times oversampling filter shown interpolates, via its filter program, data points (color) between the actual samples (black) supplied from the CD player. It doesn't generate greater waveform accuracy by this process. The original 44.1-kHz data samples themselves contain all the information necessary for a complete reconstruction of the original audio signal. Digital interpolations are stairstep expressions of what an analog filter does on a continuous, non-quantized, non-resampled basis -analog filters inherently produce smooth waveforms.
In Figure 3 you can also sense the closeness-to-the-lurking analog-waveform syndrome that is characteristic of the preceding diagram. But there is something new implied: that a digital filter is so benign as to leave the original data unaltered--that is just fills in the gaps. Ideally, a filter could be designed so that this happens, but the requirements for real-world filters (finite-lengths impulse responses, flat passband responses, etc.) make that impossible. A digital filter recalculates every sample, old or new.
Though I haven't checked all digital filters, I believe that none of them allows the original data to escape unscathed.

Figure 4. The ringing from both analog (left) and digital (right)
filters is not audible unless its duration exceeds perceptual thresholds.
This does not occur with CD-player output filters of either variety.
The waveform comparisons in Figure 4--now becoming obsolete with the pervasiveness of digital filters--are also misleading (which is why High Fidelity is no longer running them). The "ringing" of a brick-wall analog filter is clearly visible at left, in a scope photo that seems far from the original waveform (a tall, rectangular, 22-microsecond pulse). The symmetrical pulse to the right looks much nicer, but it sounds precisely the same. The ringing in the first is a consequence of the analog filter's nonlinear phase shift The symmetrical "pre-ringing" and "post-ringing" visible in the second are what a sharp-cutoff linear-phase filter does to the same signal. Both analog and linear-phase digital filters smear out frequency components to create waveform ringing. As long as the ringing in either case does not exceed perceptual thresholds, it will not be audible. It is theoretically possible to have very long pre- and post-ringing in a digital filter-which, if it were to exceed phase-audibility thresholds, would make it sound as bad as an analog filter with the same amount of ringing.
The "visuals" in Figures 2-4 are so seductively persuasive that the point I am trying to make bears repetition: No amount of connect-the-dots, fill-in-the-blanks processing--call it resampling, oversampling, interpolation, curve fitting, or whatever--whose purpose is to remove already-inaudible spectral images will pro duce audibly superior results just because it is done digitally. In fact, audible degradation can occur with digital processing, if it is done poorly (the math done wrong, which has happened, or the arithmetical problems of rounding off and truncation solved in correctly) or if the attached high-speed DACs are severely non linear or otherwise inferior.
Now, don't get me wrong. I have nothing against a well-de signed and well-executed digital filter. Most of my favorite CD players use them. But I take strong exception to the continued use of quasi- and pseudoscientific concepts and misleading artwork to promote virtues for digital output filters that are, at best, audibly suspect. Some of those favorite players have received this treatment--which does nothing to increase my valuation of the technical competence of the respective manufacturers, or at least of their public relations departments. Just remember this simple advice: Pay no attention to any claims of enhanced CD sound quality through the use of linear-phase digital operations on either ultrasonic signals or on high-frequency waveforms. You can't hear the former at all, and the circuitry of your ear/brain system conspires to keep you from perceiving the "improvements" in the latter.
Also see:
Bits & Pieces -- The real reason to want an 18-bit CD player. (Jan. 1988) DAVID RANADA
Audio Fetishes--True-life tales of strange audio beliefs.