By Jack Webster
For speed and accuracy, the binary code needed to instruct a microprocessor is converted into one of the condensed codes.
A number of different codes are used for converting decimal numbers into a more simple system for controlling a microprocessor. Two important ones are the octal code and the hexadecimal code.
Machine language
It is important to remember that a microprocessor can operate only with binary numbers. Most present day microprocessors require combi nations of eight Binary DigITS (bits); each 8-bit combination is called a byte.
The following is an example of a byte that commands a 6800 micro processor to add the contents of accumulator B to the contents of accumulator A: 0 0 0 1 1 0 1 1
An accumulator is a form of short-term memory; each accumulator holds a byte of data. In the previous example, accumulator A has been loaded with one byte of data and accumulator B holds another byte. The 00011011 instruction commands the microprocessor to add together the two bytes that are stored in the two accumulators.
It is not difficult to write a single instruction in binary form. This type of instruction is called machine language. However, a single pro gram (group of instructions) might consist of 300 instructions. Such a large number probably would pro duce too many errors when copying the program into a microprocessor.
Octal code
Figure 1 shows how the 8-digit byte is converted into the more convenient octal code. First, the binary number is divided into three sections, beginning at the right.
Notice that a zero must be added to the section at the left to complete the third 3-digit number.
Table 1 reviews the various number systems, and it can be used for reference during the conversion examples that follow.
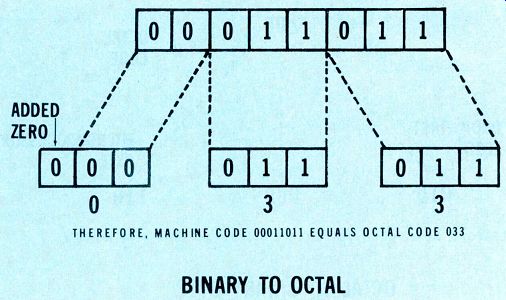
Figure 1---An 8-digit binary machine code byte is converted to octal
code by adding a zero at the left and arranging in groups of three.
THEREFORE, MACHINE CODE 00011011 EQUALS OCTAL CODE 033
BINARY TO OCTAL
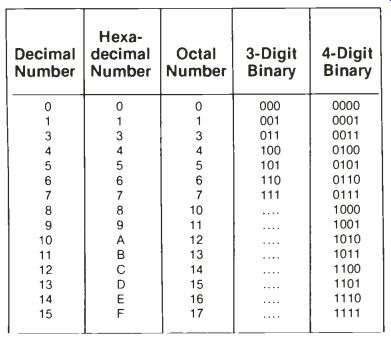
Table 1 Conversions between decimal, hexadecimal, octal and binary are
made easy by this table.
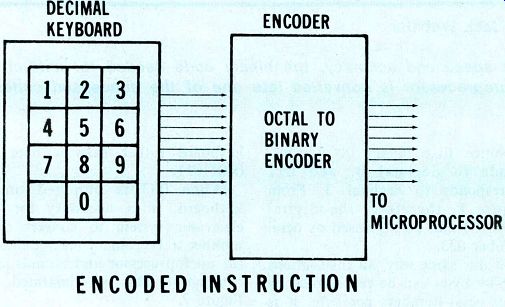
Figure 2---When decimal 033 is punched on the keyboard, the instruction
00011011 is delivered to the microprocessor.
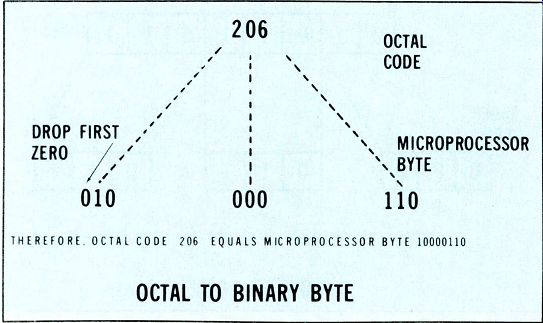
Figure 3---Conversion from octal instruction 206 to machine code 10000110
is illustrated here.
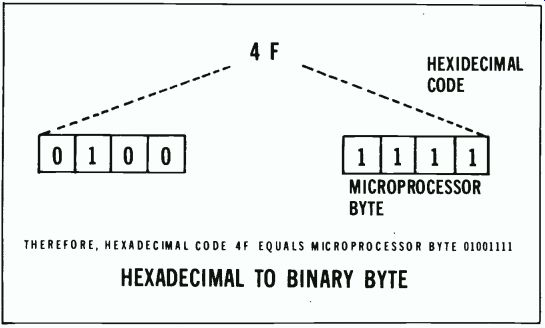
Figure 4 --- This is the method of converting hexadecimal 4F to machine
code 01001111.
Notice that binary 000 corresponds to decimal 0, and 011 corresponds to decimal 3. From Figure 1, therefore, the digital 00011011 can be expressed as octal number 033.
In this same way, all instructions in 8-bit bytes can be represented by three octal numbers per byte. It is easier and less error-prone for an operator to punch 033 on a keyboard rather than a byte of 00011011.
When 033 is punched on a keyboard, it is necessary for an electronic system to convert that number to the binary machine code the microprocessor understands and can obey. This is illustrated in Figure 2.
After the octal code for a microprocessor instruction is known, it is easy to determine the required binary byte for the micro processor. For example, the 6800 octal code for loading the contents of the memory into accumulator A is 206 (this code is provided by the manufacturer). Figure 3 shows the procedure for converting this octal code to the binary byte.
Each number of the octal code is divided into a 3-bit binary number and the left-hand zero is dropped.
The maximum allowable value of the first digit in the octal code is 3 (binary 011) so a left-side zero is always present.
Hexadecimal code
A hexadecimal code may be used instead of the octal. Use Table 1 for a review of the hexadecimal count. Sixteen symbols are needed for the 16 numbers of the count.
The 10 Arabic numbers of the decimal count are used in addition to the first six letters of the English alphabet (traditionally, only capital letters are used here).
According to the manufacturer, the hexadecimal code 4F clears the contents of accumulator A. In other words, the number in accumulator A is replaced by digital lows when the hexadecimal code 4F is delivered to the microprocessor.
Figure 4 shows how the hexadecimal code 4F is converted to an 8-bit byte for instructing the micro processor.
A flow chart is used to show the step-by-step procedure needed to place a program into effect. A diamond-shaped block in a flow chart indicates that a decision is to be made by the microprocessor, and Figure 5 shows an example of this kind of step. In this case, value B is subtracted from A and then a decision is made about the answer.
If the answer is equal to or less than zero, an alternate path is taken to the right (in this example).
Otherwise, the regular program is to be followed.
The alternate path (to the right) is called a branch or a jump.
Branching is done with the 6800 microprocessor by order of the machine code 00101111. Conversion of this machine code to the more convenient hexadecimal code is illustrated in Figure 6.
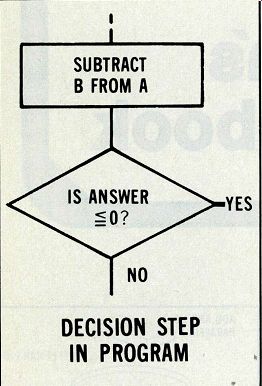
Figure 5---A diamond-shaped block in a programming flow chart indicates
that the microprocessor must make a decision based on the previous step.
DECISION STEP IN PROGRAM
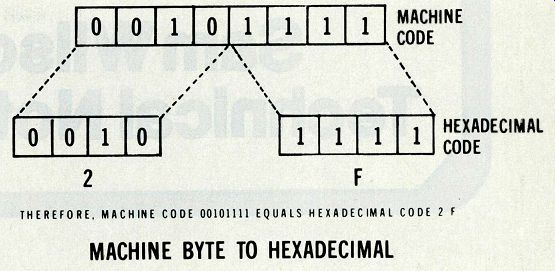
Figure 6---According to the example, binary byte machine code 00101111
equals 2F hexadecimal code. THEREFORE, MACHINE CODE 00101111 EQUALS HEXADECIMAL
CODE 2 F MACHINE BYTE TO HEXADECIMAL.

Figure 7---A 5-digit binary number at the output of a microprocessor
can have 32 possible Baudot code symbols. BAUDOT CODE.
Baudotcode
The previous coverage has concentrated on codes used for instructing the microprocessor. But the output of the microprocessor is also in binary machine language.
Normally, this output is converted into an alphanumeric readout. That is, the readout has letters of the alphabet and Arabic numbers.
One method of obtaining an alphanumeric readout is to deliver the microprocessor output coded signal to a teletype machine. The Baudot code (Figure 7) is used for this purpose.
A 5-digit binary number has 32 possible Baudot symbols. If code 11011 preceeds the printout, the bit numbers that follow represent the figures column. For example:
11011 (FIGURES)
10101 (6)
10011 (2)
From those three codes, the machine prints the number 62. Also, the following bit numbers would print the word PIN:
11111 (LETTERS)
10110 (P)
00110 (I)
01100 (N)
Additional printout codes will be discussed in a future article.
Also see: