By Jack Webster
Mathematical calculations in a microprocessor are performed by the Arithmetic-Logic Unit (ALU). The ALU uses combinations of digital gates to add binary numbers. Sometimes it subtracts binary numbers by addition.
Basic sections of microprocessors that have been described so far in this series are the ROM and RAM types of read-only and read/write memory. The most common codes for operating microprocessors also were discussed. One major section remains-the arithmetic logic unit.
Arithmetic logic unit
As the name implies, the arithmetic logic unit (ALU) can handle binary inputs as though it is any one of many possible logic gates, or a combination of logic gates. In other words, proper programming of an ALU arranges the internal logic gates into the combinations required to do binary mathematics.
For example, a certain code causes an ALU to set up the equivalent of a NOR gate. With inputs A and B, the output is ATS The fundamentals of logic gates were presented as part of the Industrial Electronics series by Sam Wilson in the January through November, 1978 issues of Electronic Servicing.

Figure 1 The 24-pin 74181 ALU integrated circuit can be used to verify
binary mathematical operations.

Table 1 These logic levels applied to the 74181 ALU function-selection
and mode-selection pins allow the ALU to duplicate any of 15 gates.

Figure 2 Any digital device that can operate by this truth table must
be an OR logic gate. The 74181 ALU can duplicate an OR and 14 other gates.
Integrated circuit ALU
A popular ALU is the 74181 IC. Table 1 summarizes the logic capability, and Figure 1 shows the pinout connections.
Programming the 74181 to function as an OR logic gate requires the following logic states: a high at the mode-select pin M highs at function-selection pins S3, S2 and S1 a low at function-selection pin S0.
Under those conditions, two inputs (A and B) can produce the proper OR gate A+B output. Lows at both inputs give a low output, and either or both inputs high produces a high output (see Figure 2 for the truth table). Remember that A+B=F is read as A OR B equals fanout (output).

Figure 3 The two input columns and the sum column are the truth table
of an EXCLUSIVE OR logic gate. The same two input columns and the carry
column are the truth table for an AND logic gate. This suggests that
a combination of EXCLUSIVE OR and AND gates could perform the addition
of binary numbers.
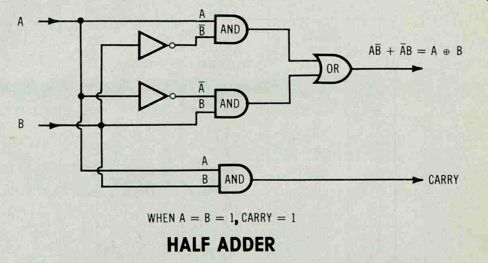
Figure 4 This combination of EXCLUSIVE OR and AND gates is called a
half adder. It adds but does not have provision for an input carry.
Arithmetic operations
The 74181 ALU IC can perform 16 arithmetic operations, and each one is accomplished by the use of basic logic gates. Keep in mind that every microprocessor has an ALU inside the IC.
It would be very educational for readers to obtain a 74181 IC and duplicate some of these basic arithmetic operations.
Adding with logic gates
Because there are only two digits in the binary system, these are the only possible sums:
The sum of 1+1 can be thought of as being 0 with a carry of 1, which is clear in the following example: Arabic
decimal binary
5 101
+5 +101
10 1010
In the decimal example, the sum of two fives is 10. The zero is marked down and the one is a carry.

Figure 5---The Figure 4 schematic of a half adder often is replaced by
a block symbol on drawings of complex digital circuits.
----------------
As a review of binary versus decimal values, remember that a 4-digit binary number has this decimal value:
1 1 1 1 binary number
8 4 2 1 decimal value (total 15)
Only binary 1 numbers have a decimal value, .so binary 0010 equals decimal 2 (zero plus zero plus two plus zero), binary 1000 equals decimal 8, and binary 0010 equals decimal 2. Reversing the procedure gives decimal 5 a binary value of 0101, and decimal 2 equals 0010.
Each of two binary 1 numbers (0001 and 0001) equals decimal 1; therefore, both binary numbers added together equal decimal 2 which is binary 0010. This should help clarify why the addition of two binary 1 numbers equal binary 10.
----------------
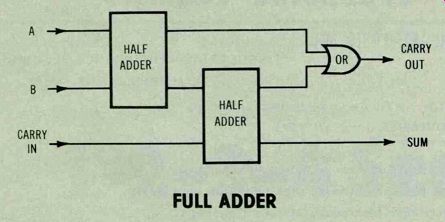
Figure 6---Two half adders can be connected to form a full adder that
has provisions to carry input and carry output.
Similarly, in the binary example, the two binary numbers in the right column are added by placing the binary 0 in the right column and carrying the 1, thus producing binary 10. This carried 1 is added to the two 0 numbers already in the center column, thus producing a 1 total (1 + 0 + 0 = 1). Next, the binary 1 numbers of the left column are added to produce binary 10. Adding these binary answers together gives binary 1010 as the answer to adding 101 + 101.
(Of course, binary 1010 equals decimal 10 [8 + 0 + 2 + 0 = 10].) A truth table for binary addition is shown in Figure 3. Study it carefully. The two inputs and the sum columns make up an EX CLUSIVE OR truth table, while the two inputs and the carry columns form an AND truth table.
This combination of logic-gate truth tables suggests that a logic circuit made up of an EXCLUSIVE OR gate and an AND gate can add two binary inputs. Such a circuit is called a half adder. Its schematic is shown in Figure 4 and its symbol is in Figure 5.
The term half adder is applied because it does not allow for a 1 carried from a previous circuit.
When two half adders are connected as shown in Figure 6, the resulting circuit is called a full adder.
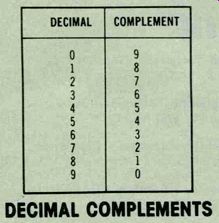
Figure 7---These are the complements of decimal numbers from 0 to 9.
Subtractions can be performed by the addition of complements.
Even a full adder is limited to A and B inputs that each have only one digit (single-bit adder). However, full adders can be cascaded to handle binary numbers of any desired word length.
Subtraction by addition
All subtraction problems can be performed by addition. This surprises many technicians at first.
The importance of subtraction by addition is illustrated by the previous circuit that only adds numbers.
After a slight modification, the Figure 6 full adder can subtract.
Decimal subtraction by addition. The complements of decimal numbers allow the numbers to be subtracted by addition. Figure 7 shows decimal numbers 0 through 9 and their complementary numbers.
Any decimal number can be subtracted from a larger decimal number merely by adding the complement of the smaller number to the larger number. Then if the sum has two digits, they must be added together to provide the final answer.
The conventional way to subtract
5 from 9 is as billows:
9 (minuend)
-5 (subtrahend)
4 (difference)
For the addition method, the subtrahend (5) is replaced by its complement (4) before the numbers are added, as shown here:
9
+4
13
This sum has two digits so they must be added to give the final answer:
1 + 3 = 4.
Perhaps an accident allowed the previous problem to work out right.
For more proof, solve the following problem: 7 (by conventional
-6 subtraction)
1
By the addition method, the problem becomes: 7 +3 (complement of 6)
10
Addition of 1 and 0 gives 1 as the answer.
This peculiar system even works with larger numbers, such as: 14 (conventional -8 subtraction) 6
However, the 2-digit number 14 must be added together to form a 1-digit number (because the complements have only one digit). 5 (1 + 4) +1 (complement of 8)
6 (answer)
Another minor variation allows the method to work with two 2-digit numbers, such as these: 18 (conventional-13 subtraction)
5
Change it to:
9 (1 + 8) +5 (1+3 = 4; complement 14 of 4 is 5)
By addition, the answer is 1 + 4 = 5.
The subtraction-by-addition system works correctly with any two numbers that have a single digit as their difference.
Comments
This article proved that digital binary numbers can be added, and also that subtraction of binary numbers can be performed by addition. Methods of using subtraction to accomplish addition of binary numbers will be presented next month.
Also see: Lightning protection