By Dale R. Patrick, Professor, Eastern Kentucky University
--- Material in this article has been adapted from Chapter 12 of Instrumentation Training Course, Volume 2, which is book number 21580 by Howard W. Sams [$11.95].---
Automation in industrial systems is possible principally because of electronic controllers. Typical applications of controllers range from simple on/off operations to huge totally automated systems that respond to signals from a digital computer. Control might be applied to only one variable (such as temperature, pressure, fluid flow or electrical conductivity), or controls might correct hundreds of variables simultaneously in a large process.
Functions and circuitry of several representative electronic controllers will be analyzed in this article. These controllers have gone through several generations. When first introduced in the early 1940s, they were equipped with vacuum tubes and mounted in large metal cabinets. With the development of solid-state devices in the late 1950s, the outward appearance of controllers was significantly changed.
The transition to all-solid-state controllers, however, has been rather slow. Initially, most companies were reluctant to give up their popular-selling vacuum-tube controllers. There was then a period when controllers employed both vacuum tubes and solid-state de vices. These "hybrid" controllers and many of the vacuum-tube devices are still in operation today. Some manufacturers still have vacuum-tube controllers available be cause the demand for them continues to be surprisingly good.
All major controller manufacturers today produce a wide variety of solid-state instruments. These units, in general, are small in size and usually employ hundreds of discrete components. Figure 1 shows a typical solid-state controller of this type. It has unusually precise control capabilities with exceptional stability.

Figure 1. A typical solid-state controller. Photograph courtesy Lees & Northrup
Company.
Figure 2. An indicating controller partially removed from its housing showing plug-in modules. Photograph courtesy Moore Products Company.
The advent of solid-state controllers has brought about some innovative design features that have had a decided impact on controller maintenance. Components, for ex ample, are mounted on removable printed-circuit cards or boards for easy replacement. Figure 2 shows an example of an indicating controller that has been partially removed from its metal housing.
The printed-circuit modules of this controller can be easily removed by pulling the wire rings near the center of the controller. This controller has a great deal of versatility through this type of construction.
Figure 3 shows a functional diagram of the potential location of alternate modules that can be utilized in this unit.
The next trend in controller technology found large numbers of discrete solid-state components re placed by integrated circuits. These controllers are somewhat smaller than their discrete component solid state counterparts. Maintenance, in this case, is based on faulty IC determination and PC board re placement.
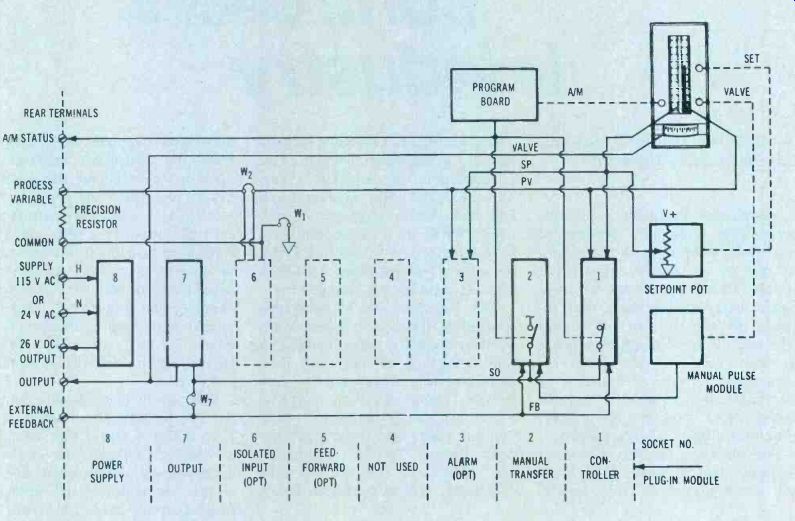
Figure 3. Functional diagram of alternate module locations for the controller
of Figure 2.
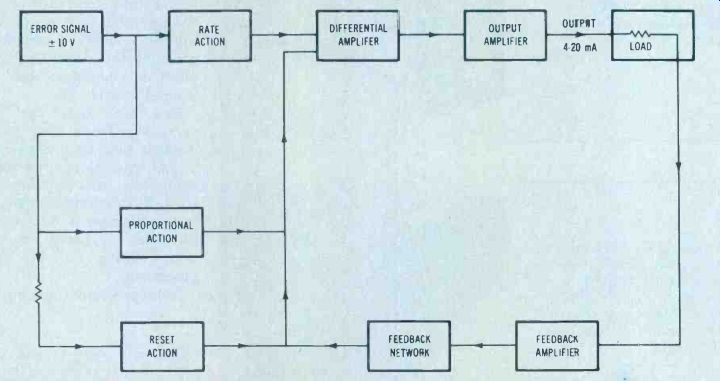
Figure 4. Block diagram of a typical controller.
Microprocessors are now finding their way into the process controller field. A microprocessor has a large number of discrete ICs on a single chip. In many situations the entire controller may be built on a single chip. This will obviously change the controller size again, and in many cases eliminate most maintenance problems.
With the wide range of diversity that exists today in controller technology, it is difficult to single out a particular controller that is representative of the field. In this regard, we will first discuss some common solid-state controller circuitry, then show some typical IC applications using op amps.
Through this approach you will be able to pick out the information that is particularly applicable to your controller needs.
Controller functions
General information Figure 4 is a block diagram of a typical controller. Three modes of operation are incorporated in this instrument: (1) proportional action, (2) reset action, and (3) rate action.
They will be discussed in connection with the input circuits of the controller.
Sections will be devoted to the rate action, differential, output, and feedback amplifiers. The controller power supply will not be covered separately because it is so similar to power supplies previously discussed.
Controller input circuits
Figure 5 is a simplified schematic diagram of the controller input circuits. Each of the three previously mentioned modes of controller operation are described here.
1. Proportional action. This action determines the ratio between the controller output signal and the input signal. If the proportional-band control is set at 100%, the controller output will result in a change that is directly proportional to the error signal. For insensitive transmitters, the proportional-band control will be set for less than 100%. The error signal will, therefore, produce an output that is proportionally greater. This is called narrow-band control. A narrow range in error signal can produce a full range of controller outputs. For settings of the proportional-band control of greater than 100%, the error signal range will be greater than the controller output. This is called wide-band operation.
2. Reset action. This action is constantly driving the final control mechanisms to zero-out any error signal. Any time the controller position differs from the set point, reset action moves the controlling device in such a direction as to agree with the set point. The amount of action depends on the amount and the length of time of the deviation.
3. Rate (derivative) action. This action determines the rate of controller action. Its effect on controller output is twofold: If the controller output rate were dependent on proportional-band control only, it is possible for the error signal to become so great that the controller could not possibly zero itself. On the other hand, if the rate action were too fast, the controller would oscillate or hunt. The error signal input to the controller is differentiated so that its rate of change can be detected and the proper rate action provided.
Figure 5 shows that the error signal is applied to a voltage divider made of R25 and R26. This signal is a dc voltage with a magnitude off 10V or less. The plug into the controller can be positioned in either the direct or reverse position.
In the direct position, a positive input produces an increase in controller current. In the reverse position, a positive input produces a decrease in controller current.
This input is fed directly to the rate-action amplifier, which will be discussed later. Its output is one of the inputs to the differential amplifier.
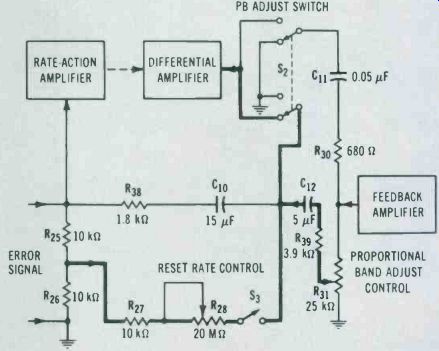
Figure 5. Simplified schematic diagram of controller input circuits.
The first input to the differential amplifier is a signal that combines reset and proportional action. One half of the error signal is developed across R20. This voltage is fed to the reset control circuit. The reset control circuit is made up primarily of R2B and C12, R27 R39, and a portion of R31 are also in the circuit. Since R2B calibrated in repeats per minute, is so much larger than the others combined, it largely determines the time constant of the circuit. This time constant determines how often the proportional response is repeated. In other words, C12 charges to the change in the error-signal voltage; R28 deter mines the length of time it takes C12 to charge. The voltage across C12 is the second input to the differential amplifier. The amplifier is stabilized by a feedback voltage that is equal and opposite to the input. How this signal is produced will be discussed in the section covering the feedback amplifier.
Proportional action is determined by the percentage of feedback-amplifier output that is applied to the differential-amplifier input. The percentage of feedback is determined by the setting of the proportional-band control, R31. The voltage at the wiper arm of R31 determines proportional action as well as a reference voltage for C12.
The reset action voltage, the charge across C12, adds to this voltage. The sum of these two voltages makes up the input to the differential amplifier. A few words need to be said about the proportional-band adjust switch, S. This switch is incorporated in the proportional-band ad just (R31) procedure by being a push-and-turn type of adjustment.
When the switch is pushed, the normal differential-amplifier input is grounded. The other pole of S2 feeds an input into the amplifier that is the charge across C11.
During normal operation, C maintains a charge that is equal to the voltage across R31. When S2 is thrown, the ground is removed from one side of C1, and applied to the input of the amplifier. Since this voltage is the same as that maintained previously, no change in output is assumed until after the adjustment has been made. The result is a smooth transfer from one proportional band setting to an other.
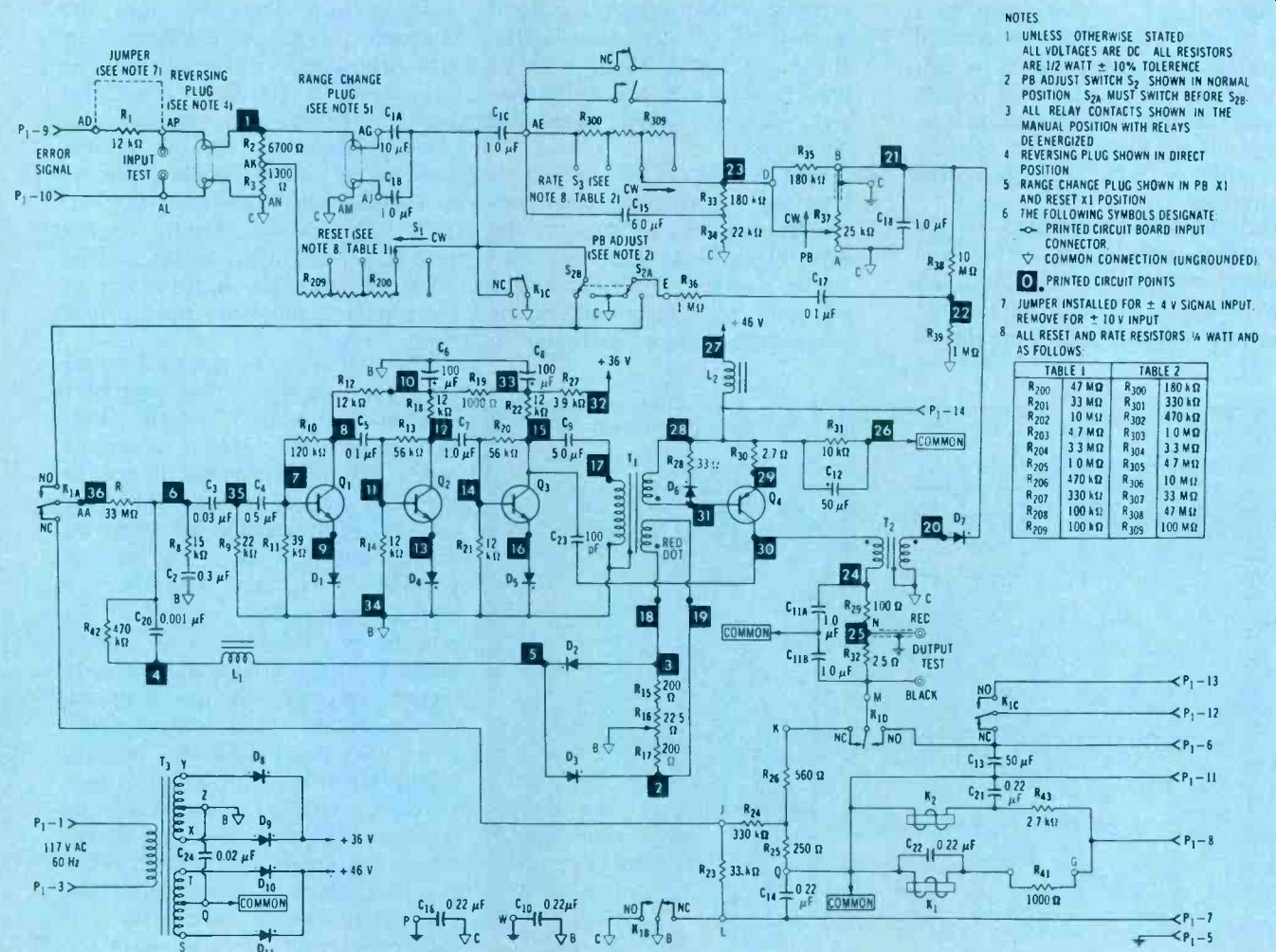
Figure 6. Schematic diagram of a typical discrete component solid-state
controller.
Solid-state controllers
Discrete component solid-state controllers have obviously not been around as long as their older vacuum-tube counterparts. Nearly all controllers sold in recent years are, however, predominantly solid state. Figure 6 shows a representative schematic diagram of a discrete component solid-state controller.
As can be seen in Figure 6, the power supply provides two dc-outputs. They are +36V and +46V, respectively. Each power supply uses silicon diodes to provide full-wave rectification.
Filtering of the power supply voltage is not quite as obvious in this circuit as is generally displayed in other schematics. The +36V source, for example, is filtered by a pi-section filter near the center of the diagram. (See printed-circuit points 32, 33 and 10.) The +46V supply, by comparison, employs an LCR filter composed of L2, C12 and R31. These components are located between printed-circuit points 27 and 26.
In the discussion that follows, we will single out specific solid-state controller circuits for explanation.
In some cases operational amplifiers will be used in circuits where this type of component finds acceptance today. Through this approach you will see how the IC simplifies the circuit and the explanation of its operation.
The controller input is the error voltage developed by the recorder.
This input signal is negative or positive, depending on whether the process variable signal is above or below the set point. When the process variable signal is the same as the set point, the input to the controller is zero. The operational amplifier circuit shown in Figure 7 is the basis for amplifier action. It consists of an input network and a feedback network in which the current is equalized by an amplifier. If the input current is constant, C in charges to that voltage. The feedback current, produced by this input voltage, charges the feedback capacitor, Ct. Once the two capacitors are equally charged, no current will conduct. The slight excess of input current necessary to sustain amplifier output is insignificant.
An input signal causes an input current to conduct, charging C.
This amplifier input immediately produces an output, or feedback current. Feedback current charges Cf to a value that equals the charge on C;n. Since the reaction of the amplifier is practically instantaneous, the feedback current is constantly tracking or following the input signal. As these two equal currents vary, adding to and subtracting from the charge of the capacitors, these charges always remain the same. As a result of this action, the junction of the two capacitors (summing junction) is always essentially at a ground potential.

Figure 7. Operational-amplifier equivalent of transistorized controller.
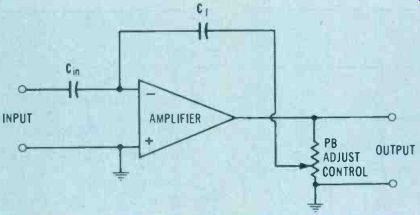
Figure 8. Proportional-band circuit.

Figure 9. Reset circuit.
Proportional action
The effective ratio of the value of the input capacitance and the feedback capacitance determines the proportional band. The effective value depends not only on capacitor size, but on the voltage gain of the amplifier. If the effective ratio is 1:1, then the proportional band is 100%. Under these conditions, a full-scale input change produces a full-scale output change. A change in the ratio of the capacitances changes the proportional band. A range of proportional bands can be provided by 1-100% or 10-1000% by changing the ratio. In addition to a variation in range of the proportional band, a change within the range is provided by a potentiometer. The potentiometer is the proportional-band adjust control shown in Figure 8. By adjusting this control, the amount of the output that is used in the feedback circuit can be varied. With a decreasing feedback signal, a larger output must be produced to fully charge Cf. An increased output for a given input is merely a narrowing of the proportional band. A full range of output signals can, therefore, be produced by small input signals. The range of input in percent that produces a full range of output signals is the proportional band.
Reset action
A voltage divider is placed across the controller input and a variable resistor is placed in parallel with Cm for reset action (Figure 9). The voltage divider and variable resistor provide a path for current whenever an error signal exists. This current provides a continuous amplifier input whenever the process variable signal differs from the set point.
Feedback current, therefore, continues to charge, or discharge, the feedback capacitor as long as there is an input. The amplifier then produces a continuous change in output as long as an input signal exists. This, by definition, is reset action, since the controlled device is seeking the null position. In discussing the proportional circuit, it was evident that there was current only when there was a change in the input signal. In the reset circuit, the only time that input current stops is when the error voltage is zero. By decreasing the value of the reset resistors, input current is increased for a given input signal. The output current must increase at a faster rate in order to produce a matching charge across the feedback capacitor. The result is a faster reset rate. Increasing the size of the reset resistors results in a slower reset rate. To produce a very low reset rate, the voltage divider has been incorporated in the input circuits. The voltage divider causes the reset resistors and the amplifier to see a smaller portion of the input signal, resulting in a smaller charging current. The input capacitor, how ever, still sees the full input voltage.
The value of the reset resistor determines the number of times that proportional action is repeated per minute.
Rate action Rate (derivative) action is accomplished by the addition of a voltage divider, a variable resistor, and a capacitor in the feedback circuit (Figure 10).

Figure 10. Derivative (rate) circuit.

Figure 11. Oscillating amplifier and output circuit.
An input signal change produces an output change that is easily passed by the rate capacitor. Since this change is taken from across the voltage divider, the result is that the feedback capacitor sees only a portion of the output. The effect is the same as a decrease in the proportional-band control. That is, the instantaneous effect is a narrowing of the proportional band.
This results in a greater output change for a given input until the rate capacitor charges. The time it takes the rate capacitor to charge depends on its time constant. This can be changed by the variable resistor, the rate time adjustment.
As soon as the rate capacitor charges, the effect of the voltage divider disappears. The proportion al band is then restored to its original value. Rate amplitude will be determined by the voltage divider. This, of course, determines the amount of the instantaneous change in signal fed through the rate capacitor.
Rate action has an anticipatory function that acts only when the output is changing. It then provides a braking or damping action. In general, rate action is used to reduce cycling and overshoot and to permit the use of narrower proportional bands.
Amplifier
The amplifier used in the transistorized controller can be divided into three basic sections: the impedance bridge and internal feedback loop, the three-stage oscillating amplifier, and the output stage.
The schematic for the amplifier is shown in Figure 11.
A Wheatstone or impedance bridge forms an important part of the feedback loop that makes oscillation within the amplifier possible. This bridge is made up of two fixed resistors, a potentiometer, and two diodes. Two legs of the bridge are resistive, while the two remaining legs are formed by the diodes.
The diodes provide rectifying action and also function as variable resistances. The amplifier output is applied across the bridge. A portion of this voltage developed across the bridge is fed to the amplifier input.
The amount of feedback is determined by the position of the bridge potentiometer. The polarity of out put coupled to the feedback loop is determined by the feedback winding of the output transformer. The polarity is such as to provide positive feedback (regeneration) at the operating frequency. The amount of feedback is determined by the bridge as mentioned previously. The frequency of oscillation, about 20kHz, is determined by the coil and capacitors located in the amplifier input circuit.
The input signal comes from the recorder. This voltage is fed to the base of Q, along with the feedback signal. If this error signal has the same polarity as the feedback signal, the output of the three-stage amplifier will increase. On the other hand, if the polarity is reversed, the output voltage across transformer T, will decrease. The amplitude of the signal across the primary of T, depends on the error signal. The three-stage amplifier is composed of three npn transistors connected as common-emitter amplifiers. The three stages are R-coupled, and a voltage divider determines the forward bias of each.
The base signal is taken from a secondary winding of T2, which is associated with Q4, a pnp transistor that is the output amplifier. Transistor collector current passes through the load for controller output. Since this current is a changing or pulsating dc, it must be filtered to give a do current range of 4 to 20mA. Collector current also passes through the primary of transformer T2. The secondary voltage, rectified and filtered, charges the feedback capacitor as discussed in the preliminary paragraphs of this section.
Vacuum-tube controllers
Using the previous controller block diagram (Figure 4) as a general reference, vacuum tubes can be used to achieve the same basic modes of controller operation as those of the transistor circuits. In general, these circuits are considered obsolete today. A large number of vacuum-tube controllers are, however, still being used in many applications.

Figure 12. Vacuum-tube rate-action amplifier.
Rate-action amplifier
Figure 12 is a simplified schematic of a vacuum-tube rate-action amplifier. This is a two-stage do amplifier. The first stage is a normal voltage amplifier and the second stage is a cathode follower. A do plate voltage for both stages is provided by 100V ac, which is rectified by D1 and filtered by C1. A negative voltage is developed across R3 by rectifier action and is maintained at the cathode of V1B by the action of C3 and D2. This develops the proper plate voltage so that direct coupling can be used with the proper bias on V1A. V1B amplifies and inverts the input error signal. The error signal input is integrated by the action of R24 and C2. By integration, we mean that the rate of change in error signal voltage is averaged out by the rate of charge (time constant) of the input circuit. If the position of C2 and R34 were reversed, the input signal would be differentiated. In both cases, the amount of integration, or differentiation, is dependent on the size of the resistor or capacitor involved.
This changing signal is fed to the grid of V1A. Static tube current maintains a constant positive voltage at the cathode of V,A. C4 assumes a charge equal to the voltage drop across R4 (the cathode voltage). During static operation (no signal input) there is no current through R5. The input to the differential amplifier is then zero volts during this period of time.
When a change of voltage occurs at the grid of this cathode follower, the cathode voltage changes. Since the charge across C4 does not change immediately (notice the long time constant of C4 and R5), the change appears across R5. Notice that only the change, or rate of variation in voltage, appears as an output of the rate amplifier. R5 and C4 make up a differentiating circuit.
Differential amplifier
Figure 13 is a simplified schematic diagram of a vacuum-tube differential amplifier circuit. Two stages of amplification are provided for the rate-action signal. Two stages also amplify the combined proportional-band and reset-action signal. These two outputs are mixed by common cathode coupling; a single output is developed that is the difference of these two input signals.
The output of the rate-action amplifier is directly coupled to the grid of V2B. Any change in tube current develops an output signal across plate-load resistor R3. R, is a common-cathode resistor for both V2A and V2B. A change in tube current of V2B changes the cathode voltage of V2A. A cathode variation provides a signal input equal in amplitude, but opposite in polarity to a grid signal. A plate-voltage change of V2A results in a rate-action input. R6 is a balance control that eliminates the need for perfectly balanced tubes. The output is V2B is directly coupled to the grid of V3A. The unbypassed cathode again feeds a signal to the common cathode of V3B. This cathode signal develops an output across R15 that is fed to the output amplifier, to which an input from the control circuit is fed directly through two stages of amplification. When two inputs occur simultaneously, the output of V, is a combination of the two inputs and is proportional to the difference in the two.

Figure 13. Vacuum-tube differential amplifier.
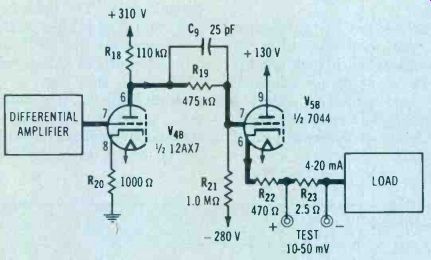
Figure 14. Vacuum-tube output amplifier.

Figure 15. Vacuum-tube feedback amplifier.
Output amplifier
The vacuum-tube output amplifier (Figure 14) consists of two stages of amplification involving tube V48, a voltage amplifier, and tube V58, a cathode follower. The input signal from the differential amplifier is fed to the grid of V,B, which amplifies and inverts it. The output of V4B is dc-coupled to the grid of the cathode-follower stage. Capacitor C by shunting R, helps prevent parasitic oscillation.
The cathode-follower stage takes the high-impedance voltage input from V4B and changes it into a high-cur rent, low-impedance output. The current output lies within the range of 4 to 20mA dc. A 2.5 resistor (R23) is inserted in series with the current output to provide a convenient test point to measure the output current in equivalent milli volts.
Feedback amplifier
Figure 15 is a simplified schematic diagram of a vacuum-tube feedback amplifier. The output-amplifier current passes through the load (0.1150 ohm) and a recorder resistor. This recorder resistor ensures a constant current output from the controller, regard less of load impedance. It also develops the input voltage for the feedback amplifier. The feedback amplifier involves two stages of amplification. The first stage (V4A) is a normal voltage amplifier that is dc-coupled to the second stage, cathode follower V SA. The voltage developed across the recorder resistor is fed to the cathode of V4A. A cathode input affects tube current in exactly the same manner as if fed to the grid with an opposite polarity. A change in cathode voltage produces a plate voltage change in phase with the input signal. The plate-load resistor, RJ4, is connected to the +310V plate supply, while the cathode resistor is connected to the-280V is maintained at about 0V so that dc coupling can be used.
The output of V4A is fed to the grid of VSA. Any change of grid voltage produces an in-phase change in cathode voltage. Tube current develops this voltage across R31 (the proportional-band control) and the parallel voltage divider, R32 and RJ1. The portion of the output voltage developed across R11 is fed back to the grid of V4A. This voltage is out of phase with the input to V4A and is, therefore, a negative feedback. The amount of negative feedback determines the gain of the feedback amplifier and stabilizes the do amplifier. The amount of feedback at the input of the differential amplifier is determined by the setting of the proportional-band control. The less the feedback voltage, the greater the sensitivity of the entire system.
This, of course, is the purpose of the proportional-band action.
As described previously, when the recorder is in the manual position, the load current is determined by the set position of the manual control. The controlled output is open-circuited. Manual load cur rent is still detected by the voltage drop across the recorder resistor.
This voltage is still fed to the input of the feedback amplifier. Feedback amplifier output maintains a charge across C12. C12, therefore, remembers the load current (the charge of C12 is proportional to load current) so that smooth, continuous operation can be maintained when switching to automatic operation.
Summary
Present-day electronic controllers usually employ discrete transistors and integrated circuits, while older models have vacuum tubes.
The three major modes of operation are proportional action, reset action and rate action.
Also see: Reports from the test lab