By Mike Hoyer
Hoyer is product marketing manager for Leader Instruments.
Bandwidth? Rise time? What are they? What factors of each do I need? Are analog and digital storage bandwidths the same?
These two areas attract the most questions by oscilloscope buyers, and with good reason. Bandwidth and rise time are the main keys to selecting the right oscilloscope for your application. Our goal is to clarify the confusion surrounding these two essential elements.
What is oscilloscope bandwidth?
The bandwidth of any oscilloscope, real-time or storage, is defined as the frequency at which a sinusoidal signal will be attenuated by a factor of 0.707, or reduced to 70.7% of its maximum value. This is called the -3dB point.
For example, a 1 V, 20MHz sine wave on a 20MHz oscilloscope would appear to be about 0.707V. This seems rather simple, and it is, but things become complex where square waves are concerned.
Square waves and video signals are some of the most complex signals. They need to be considered when choosing an oscilloscope because they are found in more and more electronic products every day. Square waves consist of an in-
finite number of sine waves: the fundamental frequency (the sine wave that is of the same frequency as the square wave) plus mostly odd harmonics (multiples of the fundamental frequency). Fourier analysis shows that a square wave consists of the fundamental sine wave plus sine waves that are odd multiples of the fundamental frequency: three times, five times, seven times and so on (third harmonic, fifth harmonic, seventh harmonic, etc.). This phenomenon is expressed in this equation:
F(t)=A sin(omega t )- A sin( omega t)/3
where A is the fundamental amplitude and cot is the fundamental frequency.
What bandwidth do you need?
The Fourier analysis calculation shows that the fundamental frequency contributes about 81.7% of the square wave. The third harmonic contributes about 9.02% and the fifth harmonic about 3.24%. Harmonics contribute to the shape of the square wave; therefore, if you remove the harmonics, it would be a sine wave. Higher harmonics con tribute less and less, and are not as significant in the creation of the square wave. This tells us that about 94% of the square wave is derived from the fundamental and the third and fifth harmonics. Inaccuracies introduced by the oscilloscope's amplifiers are about 2% to 3%, and the user's ability to accurately read the display may create about 4% error. Thus, a total minimum of 6% error is introduced by interpretation of the waveform. Therefore, 94% of the wave form's characteristic components should be sufficient.
Because a square wave is the most complex of waveforms, and because you don't really need any frequencies above the fifth harmonic of the waveform being studied, the bandwidth you will require in an oscilloscope is about five times the highest fundamental you expect to encounter. In other words, five times the highest fundamental frequency to be measured will give you the bandwidth of the oscilloscope required.
Servicing consumer products, such as TVs, VCRs, camcorders, CD players, stereo equipment and computers, re quires a 100MHz oscilloscope. The Electronic Industries Association (EIA) recommends using a 100MHz oscilloscope for these applications.
----------------------------------
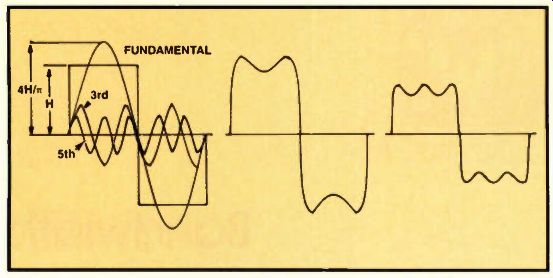
Figure 1. A square wave can be considered to be composed of a sine wave at
the square wave frequency added to an infinite number of sine waves that are
odd multiples of the fundamental sine wave frequency (odd harmonics). As this
classic illustration shows, the fundamental and the first two odd harmonics
(third and fifth) give a pretty good approximation of a square wave. For most
servicing purposes, an oscilloscope that has sufficient band width to handle
frequencies as high as the third harmonic of any square wave encountered is
adequate. The composite at the left shows the individual waveforms for the
fundamental and the first two harmonics. The waveform in the center illustrates
the resultant when the fundamental and first harmonic are combined. The waveform
at the right illustrates the wave form that results when the fundamental and
the first two harmonics are combined.
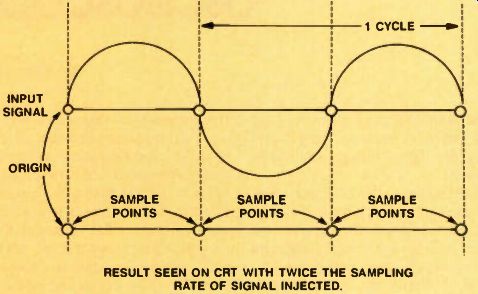
Figure 2. To assure that the waveform representation is correct, a digital
storage oscilloscope must be capable of sampling at rates greater than twice
the highest frequency that you will encounter. Sampling at less than twice
the frequency of the signal can result in a waveform that does not accurately
represent the waveform. In this worse case, a sine wave can look like a straight
line. This problem is known as aliasing.
--------------------------------------
Defining analog rise time
High-speed digital circuits contain quick rise times. The rise time needed within an oscilloscope depends upon the rise time being measured and what degree of accuracy is needed in measuring them. A 2% to 3% rise time accuracy can be obtained with an oscilloscope that has about five times the rise time of the signal being measured. Rise time can be determined from the bandwidth of the oscilloscope:
T,=(0.35)/(bandwidth)
A digital bandwidth pitfall Sad but true, determining digital bandwidth has become confusing. The sample rate of a digital storage oscilloscope must be greater than two times the highest frequency to be measured.
Think about it. A sine or square wave starts at the origin and then crosses and re-crosses the origin. In this case, if you were to sample two times faster than this signal, you would obtain two points during each cycle, and each could be at the origin. By connecting these two sample points, you would obtain a straight line.
This would lead you to believe that there was no signal at all. (See Figure 1.) How can you determine the sampling rate needed for a digital oscilloscope? Many manufacturers have developed their own rules in deciding the number of samples required per cycle of a wave form. We are not presently aware of any official agency or trade group that has actually set standards for the industry.
At Leader, we agree with the view held by the majority of engineers that 10 samples per cycle provides a sufficient representation of a waveform.
This sample rate is necessary for single shot signals or for constantly changing signals; hence the term single-shot bandwidth. There is also repetitive bandwidth, which is not related to the sample rate but refers instead to the bandwidth of the analog amplifiers.
Here, the digital storage oscilloscope obtains points over a period of several passes of the signal before displaying it on the CRT. Naturally, the signal must remain the same, or a distorted representation of the signal will result. This essentially creates a higher digital storage bandwidth, but beware -- it's only for repetitive signals. How many signals actually remain constant? Beware of varying digital bandwidth Take note if the oscilloscope has one or two analog-to-digital (A/D) converters. If the oscilloscope has one A/D converter and is in 2-channel mode, the A/D processing is shared among two channels. The sampling rate is cut in half and so is the single-shot bandwidth.
Unfortunately, many users have no idea that this is taking place.
Also see:
Oscilloscopes: From "looking glass" to high-tech