(source: Electronics World, Aug. 1964)

By IRWIN MATH / Electrical Engineer, Manson Labs Inc.
Crystal oscillators can be designed to have frequency stabilities approaching those of atomic standards. One such crystal oscillator can drive a clock so that time variation would be less than five seconds in 300 years.
ADVANCEMENTS in the fields of satellite tracking, terrestrial and extra-terrestrial communications systems, and new sophisticated types of navigation equipment for use both on and off the earth, have created a need for extremely accurate frequency and time standards. Just how accurate can be realized by a simple example. In an attempt to rendezvous two manned satellites or spacecraft a few hundred miles above the earth, an error of only 0.001 second (one millisecond) in the tracking system can cause a 30-foot error in the trajectory of the satellites. This type of error, or the long term drift of a timing source, could easily be fatal to all personnel taking part in such a maneuver.
Similarly, on the Atlantic Missile Range, exact synchronization of the various range stations is essential for accurate determination of the performance of missiles during flight.
In this application, measurement of time to accuracies of one part in ten billion (or 1 part in 10^10), over periods as long as 24 hours or more, is essential. Because frequency is dependent on time by definition, highly stable radiofrequency oscillators can be used to drive various types of indicators for both long and short term measurements.
The most familiar and widely used frequency standard is the crystal-controlled oscillator. For accuracies of parts in 10^4 (general communications and amateur radio type crystals) and higher, the quartz crystal is practically the universal frequency determining element. Schematically, a quartz crystal appears as a resonant circuit having series inductance, capacitance, and resistance paralleled by the capacitance formed by the holder, case, and electrical contacts made to the crystal. When used in an oscillator, these parameters, together with the temperature of the quartz itself, determine the final resonant frequency of the crystal. In a high-stability oscillator, it is necessary to keep these parameters as nearly constant as possible.
Variations in the ambient temperature of a crystal is one of the major causes of changes in these parameters; therefore in a highly stable oscillator, the temperature of the crystal must be maintained as constant as possible. Where stabilities of a part in 10^8 or less are required, a thermo-switched oven is usually employed.

Fig. 1. Commercial crystal oven provides 1 mc. with over-all advertised
stability of one part in a hundred million (10^8) within the temperature
range 0 to 50 °C.
Fig. 1 is a photograph of a Manson Laboratories RD-144A transistorized oscillator with a thermoswitched oven. This unit provides a 1-mc. signal with an over-all advertised stability of 1 part in 10^8 (.01 cycle at 1 mc.) or better over the range of 0 to 50 °C. A cutaway view of this oscillator (Fig. 2) shows the location of the oven (heater), mercury thermoswitch, and crystal. This entire oscillator is enclosed in a small vacuum bottle, called a Dewar flask, to prevent loss of heat.
The mercury switch deserves a little more explanation.
Fig. 3 shows an enlarged, detailed drawing of a typical mercury thermoswitch. It consists of a small thermometer to which two electrical contacts have been added. The bulb of the thermometer is attached to a threaded cap which fits into the oven shell. As the temperature of the oven rises, the mercury in the thermoswitch expands and, at the preset temperature, electrically connects the two contacts. This causes a transistorized switch to effectively disconnect the oven, stopping the heat flow, thus allowing the oven to cool. The mercury column contracts until the contacts open. At that point, the oven goes on, and the cycle repeats. Crystal oscillators such as these are used in various applications ranging from digital counters and test equipment, to standards for certain types of communications systems, as well as general laboratory reference oscillators.
For extremely high stability work, the thermoswitched oven cannot maintain a constant enough temperature, especially over widely varying outside ambient environments. For this type of temperature control (.01 °C or better), a proportionally controlled oven must be used. In this system, heat is supplied to the crystal oven at the same rate at which it leaks out or is lost. There is no switching action, but instead a smooth, continuous control is used. A commercial oscillator that uses this type of control provides output frequencies of 1 mc. and 100 kc. with an advertised stability of 1 to 2 parts in 10^10. This is equivalent to a stability of .0001 cycle at 1 mc., and .00001 cycle at 100 kc. A unit such as this is usually employed as a master oscillator in frequency control systems, as a time standard, or as a precision time or frequency marker generator. To achieve this order of stability, a proportional oven system, similar in principle to the one shown in Fig. 4, is used. Two thermistors (or other temperature-sensitive devices ) are mounted adjacent to the crystal. These thermistors, together with the two precision resistors, form a Wheatstone bridge. The bridge is connected across the output of an oscillator. The resistors are chosen so that under normal operation, the bridge is unbalanced and a signal is applied to the high-gain power amplifier. The signal is amplified to a level sufficient to cause the oven to heat and consequently raise the temperature of the crystal. As the temperature rises, the resistance of the thermistors begins to get closer to the values of the fixed resistors. This brings the bridge closer and closer to balance which, in turn, lowers the signal applied to the power amplifier and thus the heat supplied to the crystal. By proper choice of components, such a system can easily be adjusted to supply the exact amount of heat that is being lost with the result that the crystal is kept at an extremely constant temperature.
Although temperature is of major importance, there are other factors which must be considered in ultra-stable oscillator design. Voltages, for instance, applied to both the crystal and its associated circuitry must be very well regulated. Supplies with regulation on the order of x-.005 volt, and ripple of ±.001 volt or less are frequently employed.
Automatic-gain-controlled amplifiers, similar in operation to the automatic-volume-control amplifiers of a superheterodyne receiver, are almost always used to insure that the crystal current is kept at some constant value.
Various components for these oscillators are carefully chosen for minimum variation in value over long periods of time, and extreme changes in environment. In many cases, new types of circuit components have to be designed in order to meet these stringent requirements. In addition, all high-stability oscillators are kept in continuous operation to minimize crystal "aging." This "aging" is a characteristic of the quartz crystal itself, and shows up as a slow drift in frequency over an extended period of time.
In most cases, careful design of an oscillator system can reduce this drift to parts in 10^9.
By the choice of proper operating temperatures, voltages, and currents, long-term stabilities of 5 to 6 parts in 10^8, over intervals of 100 clays or more can be achieved with ease. At this rate, a clock driven by such an oscillator will lose (or gain) Only 5 seconds in 300 years! In many cases, short-term stabilities (a few minutes) can be brought well into the 10^11 region.
While a part in 10^10 may seem like a fantastic amount of stability, many of the applications mentioned in this article are already demanding even more precise standards. At the time this is written, a part in 10^11 has been achieved with a quartz crystal oscillator in the laboratory, and parts in 10^12 seem quite possible. Another approach is the atomic standard developed in the past few years. Two parts in 10^12 are being obtained today consistently with a cesium beam resonator, and +-2 parts in 10^11 can be obtained with a rubidium standard. An atomic hydrogen maser, working between nuclear hyperfine levels, may also permit the building of extremely accurate clocks.
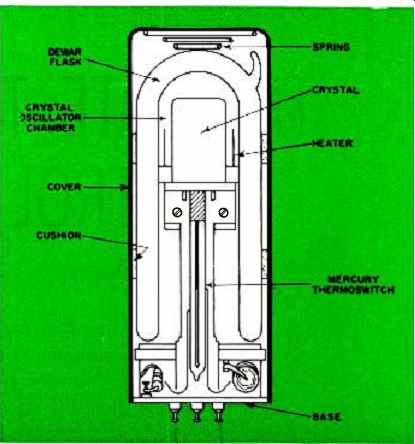
Fig. 2. Cutaway view of a commercial crystal oven shows how the crystal
is mounted in a Dewar flask and has its operating temperature controlled
by mercury thermoswitch and heater.
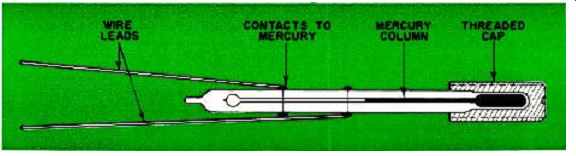
Fig. 3. When the temperature goes up, the mercury column expands to
close the electrical contacts. This action turns off the power supplying
the oven heater.

Fig. 4. The oscillator output is amplified to drive the crystal oven
heater. The thermistors are mounted adjacent to the crystal so that the
amount of power being supplied to the crystal oven is a function of how
fast the oven loses heat.
The advantage of an atomic device is that there is no drift due to "aging." The output frequency is always within the stated limits for minutes, days, and even years. Just what the final outcome will be is unknown, but as the requirements become more and more exact, it is a certainty that new approaches to frequency standards will be developed.