AMAZON multi-meters discounts AMAZON oscilloscope discounts
This guide is about electronic filters--what they are, how they work, and why they are used. Mathematics has been largely avoided and, since the guide is aimed at the practical reader, most sections end with one or two constructional projects.
These will help you to understand more about filters and their uses.
A filter is a circuit which alters the characteristics of a periodic electronic signal. A periodic signal is one which varies regularly in time. Often the signal is a varying voltage, such as that shown in Figure 1. The period of a signal is the length of time over which the form of the signal is repeated. The number of periods in one second is known as the frequency. The amount by which the voltage swings to either side of its central value is its amplitude.

Figure 1
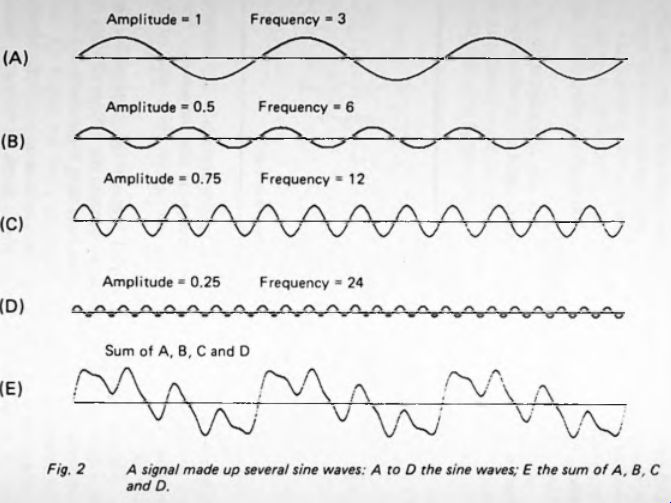
Figure 2
The signal shown in Figure 1 is one of the simplest, known as a sine wave. It has this name because the voltage changes in the same way as the sine of an increasing angle changes. Given the amplitude A and the frequency f (or the period T), and using a table of sines or the sine function on a pocket calculator, it is an easy matter to plot a graph of any sine wave.
Figure 1 is the result of plotting a sine wave using a computer and printer.
More often in practical circuits the signal consists not of just a pure sine wave but of a mixture of sine waves of different amplitudes and frequencies. Figure 2 shows such a signal and the sine waves of which it is composed. In fact, we can turn this statement the other way around and say that all periodic signals can be analyzed into a mixture of sine waves of differing frequencies and amplitudes. Even such angular-looking waveforms as sawtooth, triangular, and square waves can be considered to be sine wave mixtures.

Fig. 3. The signal obtained when the amplitude of signal C is reduced to 0.3
and signal D is eliminated.
Types of Filter
When a periodic signal is passed through a Filter circuit, the composition of the sine-wave mixture is altered. As the name 'filter' implies, a filter can not add anything to the mixture. It can only remove or partly remove sine waves of particular frequencies. There are several categories of filter, depending on what they do to the mixture. A low pass filter, for example, completely removes or at least reduces the amplitude of the sine waves of high frequency. Figure 3 shows what happens to the signal of Figure 2(E) when passed through a low-pass filter which has filtered out the highest frequency altogether, and reduced the amplitude of the next highest frequency by a little more than half. The two lower frequencies are passed through unchanged. Note that the overall amplitude of the signal has been reduced owing to the removal and reduction of some of its components. But the biggest effect is that the most rapid (that is the highest-frequency) twists and turns no longer appear.
The action of a high-pass filter is the opposite to that of the low-pass filter. It passes only the higher frequencies. Figure 4 shows the result of filtering out the lowest frequency of the waveform of Figure 2(E) and reducing the amplitude of the second lowest frequency. Now the long-term 'swell' has gone, leaving only the short-period waves.

Fig. 4. The signal obtained when the amplitude of signal B is reduced to 0.2
and signal A is eliminated.
By combining low-pass and high-pass filters in the same circuit we arrive at band-pass filters. These pass frequencies within a given range but remove or reduce the lower and the higher frequencies. The converse of a band-pass filter is a notch filter which removes or reduces frequencies in a given narrow range but passes both lower and higher frequencies.
Low-pass filters have many applications in electronic circuits. In the audio field they may be used for emphasizing low-frequency signals in the bass register, or for reducing high-frequency components of the signal, for example, tape hiss. In medical research they may be used to pick out low-frequency signals such as those originating from the brain from a confusing hotchpotch of other signals. They are often used in other applications to eliminate unwanted high-frequency oscillations.
High-pass filters are useful for selecting the treble registers in audio equipment, or for eliminating low-frequency audio components such as turntable rumble. Both types may be involved in modifying an audio signal to improve its fidelity or, as in synthesizers, to alter it so radically that sound of an entirely new quality is produced.
One of the most common uses of band-pass filters is in the tuning circuits of radio and TV sets. Here the transmission from one particular station is passed through the filter, while transmissions from stations operating on other radio-frequencies are filtered out. Band-pass filters are also important in oscillators of many types, passing the required frequency through to the amplification stage and removing all other frequencies. The reverse situation occurs when we wish to remove a particular frequency, say the 50 Hz 'mains hum', from an audio signal, for which purpose a notch filter may be employed.
In this guide we deal in detail with filters of all the above types. The projects at the end of each section provide further practical examples of the ways in which the filters are used.
Passive and Active Filters
The most elementary types of filter are constructed from resistors, capacitors and, sometimes, inductors. These are known as passive filters since they merely dissipate part of the power of the incoming signal, and pass the remainder. The advent of cheap, easily used, operational amplifiers has given scope for the design of filters which draw additional power from an external source and can actively work on the incoming signal. They can even incorporate amplification of the signal so that, although the signal has been filtered to remove unwanted frequencies, its amplitude is as great as or greater than that of the unfiltered signal. Such filters are called active filters. As we shall explain in Section 4, active filters have many advantages over the passive types, including the fact that they do not need inductors.
Digital Filters
Filtering is a matter of transforming a complex input waveform into a usually less complex output waveform. The transformation, like any mathematical transformation, is defined by a set of equations. Although few equations appear in this guide, they nevertheless exist and determine exactly what happens during filtering. In the filters referred to above we use a combination of resistors, capacitors, inductors (sometimes) operational amplifiers (often) to perform the mathematical operations required. Such circuits are, in effect, analog computers, dedicated to one particular transformation.
It is also possible to transform a signal by using a digital computer. An analog-to-digital converter is used to turn the varying signal voltage into a series of numbers, represent the voltage as converted at regular intervals of time.
We now use a computer to perform various mathematical operations which have the effect of filtering out certain frequencies. This has to be done rapidly ; usually the computer is operating in real time. The mathematically processed signal
These is then turned back into analog form using a digital-to-analog converter.
Filtering by mathematically transforming the digitized signal is known as digital filtering. Digital filters can be programmed to perform all the functions of analog filters and also, since there are almost limitless possibilities in the computations, to produce effects that are difficult to obtain by straightforward analog filters.