AMAZON multi-meters discounts AMAZON oscilloscope discounts
Resistors and capacitors are to be found in all filter circuits, so a study of the way these components behave is of importance to an understanding of filters. Inductors too, are occasionally used in filters, though less often nowadays, so we shall deal with these only briefly. Operational amplifiers replace inductors to a large extent, and their properties are dealt with in Section 4.
As its name implies, a resistor acts to resist the flow of an electric current. When a p.d. is applied across a resistor, a current flows through it. The size of current is determined by the size of p.d. which is causing it to flow and the value of resistance which is opposing its flow. There is a very simple relationship between the p.d. V, the current I and the resistance R:
V = IR
…where V is in volts, I is in amps and R is in ohms. This is an expression of the relationship known as Ohm's Law. If the p.d. is varying, for example if the resistor is connected across the terminals of a microphone or the output of an audio amplifier, the current varies in exactly the same way, instant by instant. Thus, in Figure 5, the graph which shows how p.d. V varies with time has exactly the same form as the graph of how the current I varies with time. The relative amplitude of each signal depends on the value of the resistor.

Figure 5.
Currents and Capacitors
With a capacitor, the relationship between p.d. and current is rather more complicated. Resistance has no part to play in this because the two plates of a capacitor are separated by a layer of insulating material, the dielectric. Thus no current can actually flow through a capacitor from one plate to the other. However, one particular property of capacitors leads to an interesting effect. This property is the tendency of a capacitor to hold the p.d. between its plates at a constant value. If the potential of one plate is made to rise or to fall, there is a tendency for the potential of the other plate to rise and fall by the same amount.
If a rapidly alternating current flows toward and away from one plate of a capacitor, the potential of that plate rises and falls rapidly. But the p.d. between the plates remains more-or-less unchanged. As a result, the potential of the other plate rises and falls rapidly too and by approximately the same amounts. The result is a rapidly alternating current (of the same size and frequency) flowing away from and toward the other plate. The overall effect is as if the alternating current had flowed across the capacitor. By contrast, if a slowly alternating signal is applied to one plate of a capacitor, there is time for the p.d. between the plates to increase and decrease. As the potential of one plate rises and falls slowly, the p.d. slowly increases and decreases. The potential of the other plate remains more-or-less constant. Relatively little current flows away from it or toward it. Since little current flows on that side of the capacitor, the capacitor is behaving as if it has 'resistance'. This 'resistance' is quite different from the resistance of a resistor. For one thing there is no actual flow of current through the capacitor, so there is nothing to offer resistance to. Another major difference is that this kind of 'resistance' depends on the frequency of the signal. It is low when frequency is high, and high when frequency is low. Although, like true resistance, it is measured in ohms, it is given a different name, reactance, and has the symbol Xc.
As just explained, capacitors pass signals of high frequency with very little loss. We say that they have low reactance at high frequency. Signals of low frequency are passed much less easily--reactance is high at low frequencies. To sum up, the reactance of a capacitor is inversely related to frequency.
There is one more factor that influences reactance, and that is capacitance. If capacitance is small, a given current flowing into the capacitor brings about a relatively large change of potential. On the other hand, if capacitance is high, the same current has a relatively small effect. For a given alternating signal, the changes in potential produced in a small capacitor are greater than those produced in a large capacitor. As explained above, reactance is the result of changes in potential and so is inversely related to capacitance. The reactance of a capacitor is determined by just two factors, frequency and capacitance, and is inversely related to each of them. This relationship is expressed in the equation:
Xc = 1/2 π /C.
When referring to the reactance of a capacitor we must always quote the frequency.
Phase Changes
Two alternating signals may have the same shape (for example they may both be pure sine waves) but they may differ in amplitude and in frequency. Even if they are of the same frequency they may differ in phase. In Figure 6(a) the two signals have the same frequency, but differ in amplitude.
They are in phase, by which we mean that each signal reaches the same point in its cycle at exactly the same time. They are exactly 'in step'. For example, they both pass through zero going from negative to positive at exactly the same moment.
In Figure 6(b) the same pair of signals are out of phase. They are 'out of step'. Signal B lags behind signal A by a constant amount at every stage of its cycle. Alternatively we can say that signal A leads signal B.

Figure 6.
Phase lag or lead is expressed as an angle, the phase angle, which has the symbol phi measured in degrees or radians. The length of one complete cycle is taken to be 360° or its equivalent, pi radians. In Figure 6(b) the signal B lags signal A by 34°, or 0.6 radians. We use this concept of phase angle to analyze what happens when an alternating signal is applied to a circuit containing a capacitor.
In Figure 7 an alternating signal is applied to a resistor and capacitor connected in series. Since they are in series, the same current I flows through the resistor and apparently flows through the capacitor. The p.d. V_R across the resistor at any instant is given by the equation previously quoted:
Vr =IR

Fig. 7. Voltages across a resistor and a capacitor in series.
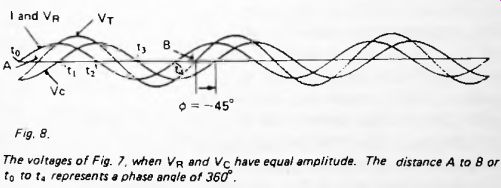
Fig. 8.
The voltages of Fig. 7. when Vp and V_c have equal amplitude. The distance A to B or to r4 represents a phase angle of 360 deg.

Fig. 9.
The voltages of Fig. 7 at low frequency. The distance A to B represents a phase angle of 360°.
The p.d. across the capacitor is calculated by a similar equation in which reactance replaces resistance:
Vc = IXc .
At any instant the total p.d. VT across the resistor and capacitor is the sum of VR and Vc. Figure 8 shows how these quantities vary in time during three cycles of a sine wave. VR varies in direct proportion to I, as would be expected from the equation above. They are in phase and, to keep the diagram simple, we have used the same curve to represent both quantities. Assume that the capacitor begins (at time t0) by being charged in the negative direction, so Vc is negative. The current flowing during the first half of the cycle (f0 to t2) completely reverses the charge on the capacitor. At time the flow of current is a maximum in the positive direction, and at that time the capacitor is being charged most rapidly, as can be seen from the fact that its potential curve has the steepest upward slope at that time. However, although it is receiving charge most rapidly at that time, the p.d. across it is a minimum as it swings from being charged in a negative direction to being charged in a positive direction. At the end of the first half-cycle (f2) the capacitor is charged to its maximum in the positive direction, and the current is zero. During the second half-cycle (t2 to f4) the increasing and then decreasing negative flow of current again reverses the charge on the capacitor.
As a result of the charging and recharging processes just described, Vc has the form of a sine wave of the same frequency as Fr and f, but is out of phase with them. Owing to the nature of the charging process, the phase difference is 90°, with the Vc lagging behind I and V_R.
During each cycle the total p.d. VT is the sum of the two out-of-phase sine waves. The curves in Figure 8 were drawn by a computer which, at the same time as it was drawing V_R and Vc, summed their values at each point and plotted the curve of VT. As the figure shows, V_T has the same frequency as V_R and VC, but is out of phase with both of them. The amplitude of the VT curve and the phase angle between this and the other two curves depends on the relative amplitudes of these two curves. The relative amplitudes are determined by the values of R, C and the frequency of the signal. This is illustrated by Figures 8 to 10. In Figure 8, the signal frequency is such that the resistance of the resistor is exactly equal to the reactance of the capacitor:
R = X_c = 1/2 pi f C
… and thus the frequency is:
I = 1/2 pi RC.
The result of this is that VR and Vc have equal amplitude.
V_T has an amplitude rather greater than either of them. It is never twice as great, since V_R and V_c are out of phase and therefore not at both their maxima at the same times. In fact, VT has an amplitude 1.4 times as great as V_R (and Vc). Also, Vc lags 45° behind V_T. We say that Phi = -45 . These relationships apply whenever R and Xc are equal.
In Figure 9 we see what happens with the same resistor and capacitor when the signal frequency is lower. The curve for Fr is as before, but that for V_c has greater amplitude as the capacitor has greater reactance at the lower frequency. The resultant curve for V_T shows it once again to have a larger amplitude than V_R or V_c, but now the phase angle has decreased to -30°.
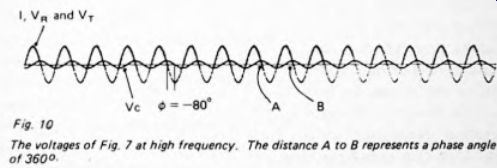
Figure 10.
Figure 10 shows the result of increasing the frequency, with the same resistor and capacitor. Now V_c has a very small amplitude and has little effect when added to V_R. The curve of V_T follows so closely to that of V_R, that they do not appear as separate curves on the plot. The amplitude of V_T is only slightly greater than that of V_R. The phase lag of V_c is now increased to -80°.
We return to the amplitude and phase relationships of V_R, V_c and V_T in the next section.
Inductors
An inductor is a coil of insulated wire which is generally wound on a core, former or armature made of electromagnetic material. The core is usually of soft iron or a ferro-ceramic material such as Ferrite. In several ways an inductor is the opposite of a capacitor. For instance, there is a continuous conduction path through its coil. The coil may have a resistance of only a few ohms, sometimes only a fraction of an ohm. It offers negligible resistance to the passage of a steady electric current. But the operative word in the previous sentence is 'steady', meaning direct current. When the current is an alternating one, electromagnetic effects come into play.
When current flows through a coil a magnetic field is generated. It is a property of such coils that there is opposition to anything that would tend to change the intensity and direction of that magnetic field. The more rapid the change that is attempted, the more strongly is that change opposed. With no change there is no opposition, which is why a steady current can flow freely through the coil. With a moderate change, such as would be produced by a low-frequency alternating current, there is moderate opposition. Such a signal passes through the coil, with a small amount of loss. With a rapidly changing current, such as that resulting from a high-frequency signal, there is strong opposition. Very little current is able to pass through the coil. Thus the inductor offers a varying 'resistance' to the flow of alternating signal currents.
As with the capacitor, this is not true resistance for we have said that the coil has extremely low resistance. This 'resistance' is known as inductive reactance, and is given the symbol XL to distinguish it from capacitive reactance XC1 It depends on two factors, one of which is the self-inductance L of the coil. This is determined by the number of turns in the coil and its physical dimensions. The other factor is frequency and the two may be combined together in the equation:
XL = 2 pi fL.
This expresses the fact that inductive reactance increases with increasing frequency, the opposite behavior to capacitive reactance. Given that inductors have frequency-dependent reactance, it is plain that they can be used in a similar way to capacitors, except that the circuits operate in the reverse manner. Filters can certainly be built with inductors but there are disadvantages. One is that inductors tend to be large, heavy and costly. Another disadvantage is that it is not easy to make an inductor with an accurately specified self-inductance. They also have the annoying property of picking up interference from any electromagnetic fields in the neighborhood.
Finally, it is so much easier, cheaper and more precise to replace the inductor with a circuit based on an operational amplifier. About the only remaining use for inductors in filtering is when we wind a few turns of wire around a ferro-magnetic ring, or thread the wire through ferromagnetic beads to filter out radio-frequency signals.