AMAZON multi-meters discounts AMAZON oscilloscope discounts
The filters previously described in this guide have all dealt with continuously variable quantities--voltages or currents that can have any value within a given range. This is the result of the nature of the components, the resistors, capacitors and amplifiers used in building them. Such filters are referred to as analog filters. In this section we look at filters based on digital electronics. In these we are mainly concerned with logic levels, voltages which may be high or low, but are not allowed to take values in between.

Fig. 84. A simple digitally-controlled low-pass filter.
Before we go on to discuss digital filters we must mention another category of filter that is sometimes referred to as digital or, more accurately, digitally-controlled. Figure 84 shows a simple low-pass filter of this kind. The filter works by gradually accumulating charge on the capacitor or gradually losing charge from the capacitor, in the same way as any other active filter. But the filter has a switch that can be turned on or off at high frequency by digital means. If the switch is permanently closed, the circuit behaves as a filter with cut-off point at 160Hz. This is calculated from the equation f = 1/2 pi RC, with R having the value 100 k-O. If we apply a square wave (i.e. digital) signal to the gate which controls the switch, we can arrange to turn the switch on and off at high speed. Suppose that this signal turns the switch on for exactly half of the time. The resistor now conducts for only half the time and consequently passes only half the amount of charge.
It becomes equivalent to a 200 k-O resistor, and the cut-off frequency is reduced to 80Hz. By varying the proportion of time for which the switch is closed we can vary the cut-off frequency of the filter. However, although the filter is controlled by digital means the actual filtering is still done by a resistor and a capacitor. This puts it in the same category as the switched capacitor filters described in Section 7.
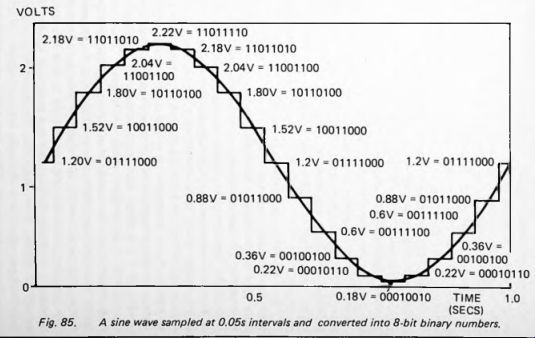
Fig. 85
In true digital filtering the signal itself is converted to digital form before being filtered. However, the signal itself is a waveform which is a continuously varying analog quantity. In the case of an audio signal the varying voltage is an analog (or an electrical representation of) the movements of the vibrating parts or air columns in the instrument making the sound. Before this analog signal can be dealt with digitally it must be converted to digital form. This is done by an electronic circuit (usually an integrated circuit) known as an analog-to-digital converter. There is not enough space here to describe how such devices operate but their function is to accept an analog voltage as input and to produce a series of digital outputs at regular intervals. The input voltage is regularly sampled and each sample is converted to produce its equivalent as a binary number. For minimal precision the binary number might consist of 8 digits (8 bits), each represented by a low (0) or high (1) voltage level. With such a converter the analog input may range between 0V and (for example) 2.55V, and take any of an infinite number of different values within that range. The output has only 256 possible values, ranging from zero (binary 00000000) to 255 (binary 11111111). Figure 85 shows the result of sampling a sine wave and converting it to an 8-bit output. It is the limited number of output values that causes loss of precision. A-to-D converters with 8-bit resolution are available cheaply but for higher resolution it is commonplace to employ converters with as many as 12 or 16 bits in their output. A 16-bit output has 65536 possible values, which is precise enough for most purposes.
Another important factor in A-to-D conversion is the sampling rate. A converter takes a finite time to sample the input voltage and convert this to its digital equivalent. If sampling is too slow, the converter will not keep up with rapid changes in the input signal level. The output will be seriously distorted. As a general rule, the sampling rate must be twice that of the highest frequency present in the signal.
For high-fidelity sampling this includes the harmonics so several tens of thousands of samples must be taken and converted each second. Many A-to-D converters are capable of a sampling rate of several hundred kilohertz. At lower rates of sampling the fact that the smoothly varying signal takes on a stepped form is equivalent to adding high-frequency components (the sudden changes in level associated with stepping). If the sampling rate is high enough, the added frequencies are higher and come well above the frequency range being considered.
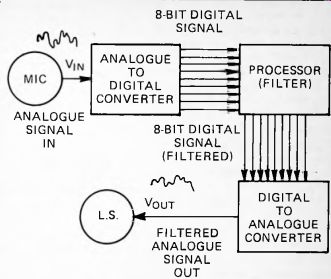
Fig. 86. The main stages in digital filtering.
Figure 86 shows the main stages of digital filtering. After the signal has been converted to digital form it is subjected to some kind of processing. We shall discuss the nature of this later but for the moment consider it to be the digital equivalent of the 'processing' performed by analog components such as the resistors and capacitors (and sometimes inductors) of an ordinary filter. If the samples are to be processed at the rate at which they are being taken, this processing must be performed by a computer or a dedicated microprocessor system. If a high sampling rate is required and the processing consists of several stages the computer may need to call upon the services of an auxiliary maths co-processor. The final stage of filtering is the conversion of the processed signal from digital form back to its analog equivalent. For this stage we use another circuit known as a digital-to- analog converter.
This performs the reverse function of the A-to-D converter, receiving a series of digital values and producing a series of voltages. Note that the output of the D-to-A converter is not a true analog signal with smoothly varying voltage. It is a stepped series of voltages. Thus if an 8-bit converter is used and the voltage range is 2.55V, the minimum difference between one step and the adjacent step is 0.0IV. This again leads to loss of resolution and the introduction of high-frequency components into the output signal. This may be made of less importance by using a 12-bit or 16-bit converter and by using a high sampling rate. An active low-pass resistor-capacitor filter may also be used to remove the high-frequency components from the output signal.
Signal Processing
Processing the digitized signal is a mathematical operation which can be as elaborate as we like and can be performed with any required degree of precision. This means that the expense of high-precision resistors and capacitors is avoided, even supposing that components of the required values are actually obtainable. In digital filtering a few mathematical steps can replace several stages of resistor-capacitor filtering.
These two factors tend to make digital filters cheaper than the equivalent high-precision filters of the analog kind. Furthermore, by slightly altering the processing program to change one or two parameters, we can alter the filtering characteristics in a way that would normally require ganged variable resistors.
These are usually difficult and expensive to obtain and, even then, may not work entirely as required. Another advantage of digital filtering is that it is just as easy, if not easier, to filter very low frequency signals which would require exceptionally or almost impossibly high-value capacitors in an analog filter. The effect of temperature on resistance and capacitance is another bugbear that has absolutely no bearing on a digital filter. Finally, it is possible to use processing routines to filter signals in ways that could not be achieved with passive or active components.
As a simple example we look at the operation of a digital low-pass filter. In the analog equivalent the charge on the capacitor at any instant is dependent on the previous input to the circuit. At any instant the voltage depends most on the most recent voltage level of the signal and to a progressively lesser extent on voltage levels present further back in time. To be able to manipulate this we need to divide time into a series of distinct intervals, corresponding to successive samples.
Suppose that the signal is a sawtooth wave and that the first 5 successive samples of this are as shown on the left of Figure 87(a). The sampling rate shown here is too low to be of use in a practical filter but having only a few samples makes the calculations easier to understand.
We can now define the characteristics of a particular digital filter by saying that, at each sampling time the signal value (corresponding to the charge on the capacitor) is equal to the current sample, plus half of the previous sample, plus a quarter of the previous sample, plus an eighth of the previous sample, plus one-sixteenth of the previous sample. Samples earlier than these are to be ignored.
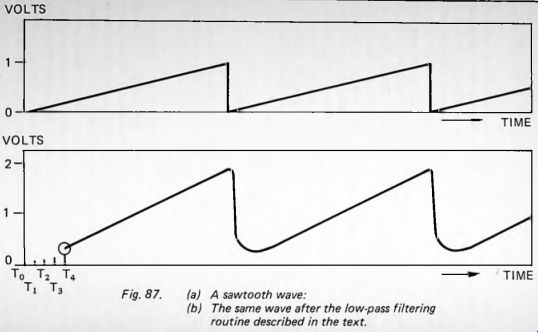
Fig. 87
Thus at time f4 the signal value is:
^4 "F ^3/2 4- ti/4 + ti/8 + to/16 .
Putting in the values of these five samples, their total is:
0.2 + 0.15/2 + 0.1/4 + 0.05/8 + 0/16 = 0.30625
This is the first point plotted on the graph of Figure 87(b). The next point, at ts, is calculated in a similar way, but based on values at tx to ts. This process is repeated for each time point, always basing the value on the current value and the previous four signal values. When this is done and the points are joined, the resulting curve (the output signal) takes the form shown. The sawtooth shape is still obvious, but its 'sharp points' are rounded off. In other words, the more rapid changes of level have been reduced; the higher frequencies have been 'filtered' out. This is a low-pass filter.
The calculation described above produces one sort of low-pass filter with a particular cut-off point. By varying the routine in different ways it is possible to produce other low-pass filters. For example, we could increase or reduce the number of recent samples taken into account. Or we could have a different series of divisors, for example:
t4 + t3/3 + t2/6 + t1/9 + t0/12 .
Without becoming involved in building the hardware, it is interesting to write short computer programs (as was done for the graphs of Fig. 87) to investigate the effects of such routines on a given input signal.
Other routines can readily be devised and programmed for performing other types of filtering. One feature of a routine may be to take the output of the first stages of the calculation and add a portion of this into the second stage of the calculation. This is the equivalent of using feedback, as we do when using operational amplifiers in active filters. With a little mathematical know-how it is possible to program low-pass, band-pass and high-pass filters of all the well-known types, such as Butterworth, Chebyshev and others. With a little more expertise it is possible to produce filters of a variety of bizarre and otherwise unrealizable types.
PROJECT 12--Discriminating Baby Alarm -- Level 2
A project based on digital filtering of the kind described above would not only be higher than 'level 3' but would need an interface to a microcomputer and require the reader to be familiar with programming in assembler. Instead, recalling the remarks made earlier in the section about digital filters being able to operate on very low frequency signals, this project is a rather specialized type of filter. As with Project 1, its function is to filter out unwanted signals.
If we consider the sounds likely to be heard whilst baby is supposed to be asleep, there are two main types:
(1) Short-period sounds; sporadic contented snuffles, an occasional sneeze or hiccup, the sound of baby's hand striking the cothead as he or she turns over, the sound of a door slamming or the window rattling (this door may be the door of another room, but it may nevertheless be picked up by the microphone beside the cot), the sound of passing traffic, and other transitory and unimportant sounds.
(2) Long-period sounds: baby wakes up and begins to babble, shout or cry. Baby needs attention! The purpose of this project is to discriminate between these two types of sound, to ignore the first and to call the baby-minder's attention to the second.

Fig. 88. Project 12: Discriminating Baby Alarm.
How It Works
The basic quantity with which this circuit deals is the presence or absence of sound. The timbre or frequency of the sound is not taken into account. Presence or absence of sound is a binary quantity--there either is sound or there is not. Because of the binary (and therefore digital) nature of the sound, no A-to-D converter is necessary in this system. All that is required is a sound detector with a binary (sound/no-sound) output.
(XTAL1, Fig. 88), the sound signal being amplified by TR1 and the Darlington transistor TR2. When there is no sound the voltage at the upper end of R5 remains constant at about +2.5V. When sound is being received the voltage rises and falls, sound is detected by the crystal microphone rapidly. IC1 is an operational amplifier wired as a comparator.
The variable resistor VR1 is set so that the voltage at its wiper is just a little less than 2.5V. In practice, a level of about 1.7V has been found satisfactory. In this state the output of the amplifier is low, close to 0V.
When sound is picked up by the microphone the downward swings at R5 bring the voltage at the (-) input of the amplifier below that at the (+) input and the output of the amplifier swings high, to about 4V. This acts as a logical 'high', (or T'). IC2a and IC2b are cross-connected NOR gates acting as a bistable flip-flop. The high input to the flip-flop sets it, and the output of IC2b changes from low to high. This records that sound has been detected, a fact that is indicated by the LED D1 being switched on. A high logic level is also presented to the first stage of the shift register, IC5.
The shift register is controlled by a clock (IC3) running at about 0.45Hz, with a period of 2.2s. The ratio of the resistors means that the output of the clock is high for about 2s, followed by a low period of about 0.2s. However this output is inverted by a NAND gate (IC4a) wired as a NOT gate. At the end of every 2-second period the output of this gate goes high. This triggers a pulse-generator (IC2c, IC2d) to produce a short high pulse to reset the flip-flop. It also causes the shift register to operate. Data present at input A now appears in register 1A. If sound has been detected during the previous 2 seconds, that register now holds a logical '1'. The output from that register (pin 5) is high. The resetting of the flip-flop returns it to the state in which it is ready to record the arrival of the next sound, if any, during the following 2-second period.
The LED goes out and remains out until sound is detected.
The register is shifted at every clock period, the content of register 1A being gradually shifted down the chain to 2A, 3A, 4A, IB, 2B, 3B, 4B, and then finally being lost. Thus the shift register indicates whether or not sound has been detected during each of the previous 8 periods. In terms of a digital filter, it holds a sound sample for each of 8 consecutive periods. These samples now have to be processed. Since the samples are logic levels they can be processed logically. The purpose of the circuit is to discriminate between occasional short-lived sounds and more continuous ones. A series of occasional sounds may cause logical l's to appear in one or more registers but it is very unlikely that there will be a '1' in every register. Indeed, loud sounds occurring 8 times in 16 seconds are very likely to have woken the baby already! We are assuming a rather quieter environment. But if baby is awake and crying or talking to himself or herself continuously for 16 seconds or longer, then all 8 registers will hold *1*. The 8-input NAND gate IC6 detects this event and its output goes low. This sets the second flip-flop (IC4b, IC4c). This being made of NAND gates is set by a low-going pulse, whereas the first flip-flop, made of NOR gates, is set by a high-going pulse.
When the flip-flop is set the output of IC4c goes low. This is inverted by gate IC4d which acts as a buffer to provide base current to TR4. This is turned on and the LED begins to flash. It remains flashing until the flip-flop is reset by pressing the button SI. A flashing LED is used for D2 since this is more eye-catching than a continuously lit LED. D2 can be replaced by an ordinary LED if preferred, but then will need a 470H resistor in series with it. If audible warning is required, a low-current audible warning device, preferably with a warbling tone, can be either substituted for D2, or wired in parallel with it. Again, as with input stage, the output is binary. The alarm is either raised or it is not. For this reason there is no need for a D-to-A converter.
This device functions as a low-pass filter. It discriminates between sounds of short duration (a relatively rapid alternation between 'sound' and 'no-sound') and sounds of long duration (a slow alternation). With the NAND gate reading the contents of all 8 registers the filter responds only to sounds lasting 16s or longer. We could say that this is the equivalent of the filter's cut-off point. If you wish the device to respond to sound of shorter duration--to reduce the cutoff point--some of the connections between ICS and IC6 can be rewired. For example, to give a 10s cut-off point (5 clock stages) remove the connections from the outputs of registers 2B, 3B and 4B. Instead, wire the corresponding inputs of IC6 to the +6V line. The circuit will then respond when the first 5 registers each hold '1'.
Construction
The circuit requires only 20mA when quiescent so it can be operated for considerable periods on a 6V battery. In the long run it is more economical to use a 6V DC mains power supply unit. The circuit consists of only 6 ICs so can be housed in a small plastic case. If it is convenient to place this close by the bed or cot, the microphone may be mounted in the case behind a grille consisting of an array of fine holes drilled in the side of the case. Alternatively, the microphone can be on a lead. The lid or panel of the case carries the sensitivity control (VR1), the indicator LED (D1) and the reset button (S1). The warning devices (D2 or AWD or both) are located in the living room, connected to the main circuit by a pair of light-duty wires.
Build the clock first and check that it runs at the correct rate; it is possible to increase the time-scale of this filter by using a capacitor of larger value for C2. Next build the amplifier and comparator section, together with the pulse-generator and flip-flop (IC2a-d). Also connect Gate a of IC4.
While testing at this stage connect the unused inputs of IC4 to the 0V or +6V lines. To check the circuit measure the voltage at pin 2 of IC1, then set the sensitivity adjustment to bring the voltage at pin 3 about 0.5V lower than this. The output at pin 6 is low and, at the next clock pulse, the flip-flop is reset and D1 goes out. Any small noise made near the microphone sets the flip-flop and Dl comes on. It goes out again at the next clock pulse.
Now add the shift register, IC5 and the 8-input NAND gate. As mentioned earlier, it is not necessary to connect all 8 registers to the gate, but all inputs to IC6 must be connected to something, either to IC5 or to the +6V rail. If you wish to allow the discrimination period of the filter to be variable, a rotary switch could be included here to allow different numbers of registers to be connected to IC6. Testing at this stage shows that the output of IC6 (pin 13) is normally high and stays high in the absence of sound. If you make a sound each time the flip-flop resets (i.e. each time Dl goes out) then Dl comes on again each time and the output of IC6 goes low after 8 such noises. But if you make a sound only occasionally, not after each of 8 consecutive clock pulses, the output of IC6 stays high.
Complete the circuit by building the NAND flip-flop of IC4, and wiring its output through IC4d to TR4. Add the flashing LED and possibly an audible warning device.
To use the alarm, first set the sensitivity control (VR1) so that D1 comes on whenever a sound of sufficient loudness is made. If the bedroom is by a noisy road or there are other frequent sources of sound, it may be necessary to position the microphone closer to the cot or bed and to reduce the sensitivity. Making as little noise as possible, press the reset button and hold it for 2-3 seconds until D1 goes out. D2 then stops flashing. If you make a sound when leaving the room or closing the door, this will not normally matter because the filter rejects it as a short-period sound.
Special Components
XTAL1 is a cheap crystal microphone; a 'microphone insert' is very suitable.
VR1 is a panel-mounting Volume control' carbon potentiometer, complete with a knob.
D1 is an ordinary LED, but D2 is preferably one with built-in flashing circuit. If audible warning is required, use a solid-state audible warning device or electronic 'buzzer' suited to operating on 6V.
The ICs are as follows:
CA30140E CMOS operational amplifier 4001 CMOS quadruple 2-input NOR gate 7555 CMOS timer 4011 CMOS quadruple 2-input NAND gate 4015 CMOS dual 4-stage shift register (serial-in parallel-out) 4068 CMOS 8-input NAND gate.
IC1 IC2 IC3 IC4 IC5 IC6