During nearly 20 years of association with audio and tape recording, I have noticed that technical development tends to be quite faddish. The "in" thing recently has certainly been phase and phase distortion. It really doesn't matter which transducer holds one's interest: Articles and ads can be found in profusion, extolling the virtues of some new technique, or imploring the purchase of some new and expensive piece of equipment. "Transducer" is the key word here the only electronics which possess any measure of phase shift or distortion are those designed to correct for the nonlinearities of some transducer (speaker, phono cartridge, tape head, etc.) in the audio system.
But what is the point? Didn't Herr Doktor Professor Hermann Ludwig Ferdinand Baron von Helmholtz himself say that tone quality did not depend upon the relative phase of its components?' Yes, indeed ... but the statement was very carefully qualified, and Helmholtz tabulated some exceptions. Even those who say that individual system phase distortion is not audiblez'l will agree that phase differences between stereo channels will displace the stereo image, but the situation is worse than that. I don't intend to take a lot of space here to defend my point of view, but for the purposes of this article I will take the position that certain types of phase distortion are important to audio. The conditions and qualifications will be carefully stated. If you need to be persuaded, I can only recommend Schroeder's marvelous paper,' which convinced me beyond a doubt.
Phase
Few readers of this magazine are totally ignorant of what is meant by the terms phase and phase shift, but there is so much confusion in the literature that it's best to start off with some "basic basics" that we all know. I'll define terms as I go, so that nobody (including me!) gets lost as things get more complicated.
A single frequency can be represented as a constantly rotating vector of constant length, called a phasor. To see how this can represent the thing we generally call a sine wave, see Fig. la. The phasor rotates with one end fixed at "P," and the other end describes a circle. The phasor starts with its moving end at "O." At the end of a certain amount of time, the moving end is at "a," and the phasor has rotated through an angle "A." At the end of twice the first interval of time, the end of the phasor is at point "b," and the rotation has been through an angle "B." which is exactly twice angle "A." This is continued around the circle.
A Cartesian graph is now constructed, with the abscissa extended from the line through the center of the circle and point "O." The abscissa is marked off into equal intervals, and coordinates are erected at each point, labeled to correspond with the points around the circle. Horizontal extensions are made from point "a" to ordinate "a'," from "b," to "b`," etc. A continuous curve (solid line) is drawn through the points where extensions cross their corresponding ordinates. This curve is known as a sine wave. It is a plot of amplitude vs. time of a single frequency. Points along the wave can either be measured by time or by the angle of the phasor. This measurement is known as the phase or the phase angle. Phase is measured either in degrees (360° for a complete circle) or radians (2 pi = 6.283... for the circle). The points on this particular graph are 20° or pi/6 radians apart.
The frequency of the signal is just the number of times per second that the phasor makes a complete circle. The angular frequency is the number of radians per second through which the phasor rotates or just twice the frequency. Phase shift of one sine wave with respect to another can be thought of as if there were a horizontal relative movement of the wave along the abscissa (time axis). In Fig. 1A, the wave shown by the dashed line lags the one shown by the solid line by 90°.

Figure 1A--Construction off a sine wane from a phasor. The phasor is of constant
length and has one point fixed at "P." It revolves around "P" with
a constant angular velocity. At the end of each unit of angular rotation, the
point at the end of the phasor is projected to the proper ordinate representing
a unit of time. The height of the ordinate at a' (for instance) is given by
h(a') = L sin A where h(a') is the height at a', L is the length of the phasor,
and A is the angle of rotation at a. Because of this relationship, the locus
of the points is called a "sine wave." The dashed sine wave is of
the same amplitude, but it has been phase shifted by 90 degrees.

Figure 1B--Three sine waves of different frequency with the same initial phase;
f, is the fundamental, f2 is the second harmonic (f2 = 2f1), and f is at half
the frequency of the fundamental. The 90" phase points m90(f,), 090(f2),
and m9o(f1/2) occur at different times, t2, and tri respectively. For a fixed
time delay tx, the phases are different: m(f,) = 90°, Ott) = 180°, and D(f2)
= 360°.
Complex Waveforms
More complicated waveforms can be constructed by adding together sine waves of different frequencies. These frequencies are harmonically related, which means that if the fundamental frequency is denoted by f3, the only other frequencies present are the harmonics of f1, that is f2 (= 2f1), f3 (= 3f1), etc. A square wave, for instance, can be constructed with the fundamental (at the same frequency as the square wave) and its odd harmonics, as follows:
Frequency | Amplitude | Phase Shift

with the additions continuing indefinitely. Actually, the frequencies do not go upward without limit in any real system, but the amplitudes of the highest harmonics are so small that they don't contribute very much. If the proper harmonics with proper amplitudes are added, but the phase relationships are different than shown, the result is not a square wave at all. It may not even be recognizable as a distorted square wave if it is viewed on an oscilloscope screen. Nevertheless, what Helmholtz said, is that the ear is sensitive only to the frequencies and the amplitudes, and not in any way to the phase relationships of the various harmonic frequencies. This has been shown many times since by many experimenters, giving rise to such absolute statements as that found in reference 5, "... there is almost overwhelming evidence that preservation of waveshape is of no significance and that in consequence phase shift in a monaural channel is of little importance ... . The problem with positions such as this is that one tends to forget that there is very little information in a continuous wave, no matter how exotic its shape. Not many people settle down in their living room chairs for a few hours of easy listening to their favorite square wave! Almost all the information found in speech and music is in the changes found therein, changes in frequency and amplitude, including starts and stops. It also seems obvious that fundamentals and harmonics must not arrive at audibly different times from each other, so the timing of the changes is important. What all this means, is that the transient response (response to changes in the signal) of the system is of great importance and it is possible for certain types of phase distortions to give rise to audible transient effects.' Time The phase shift shown between the solid and dashed curves in Fig. 1A can be regarded as a time shift as well. This particular one has a time lag of three units of time. If the frequency was twice that shown, a time lag of three units would give twice as much phase shift, or 180". For half the frequency, the three units of time shift would give half the phase shift, or 450. Thus, a constant time delay creates a phase shift proportional to frequency (Fig. 1B). A constant time shift causes no problems, or recordings could not be made now, stored, and replayed later.' Neither is the ear sensitive to a phase shift which is a constant number of degrees for all frequencies. The time delay for a given amount of phase lag is greatest at the low frequencies, and smallest for the high frequencies (Fig. 1B, see how the 90° phase points as a function of frequency affect the time delays in Fig. 1A). This sort of phase change does change the waveshape, as has been previously noted, but the ear ignores it. Of course, if there are two stereo channels with different amounts of phase change, the stereo image will shift its location'. Except for minor effects which are caused mostly by nonlinearities in the inner ear, the important effects reduce to two categories, each with two subcategories: 1) Relative time delay, comprised of a) channel-to-channel time delay in a stereo presentation,' and b) frequency dependent time delay' (this is the same as saying that the phase shift is not a linear function of frequency,' and 2) any phase changes in a system when the signal has a positive/negative asymmetry in its waveform, comprised of a) transients,' and b) steady state.° So far, all of the design effort has been concentrated in dealing with category number 1. Compensating for category no. 2 would require the setting of a phase standard (i.e., if the live music had a positive pressure wave at a certain point, the reproduction should also exhibit a positive pressure wave at that point). Such compensation would also open up a large Pandora's Box; for example, since the phase relations are different at every point in a concert hall, which point is to be chosen for the standard? Nevertheless, category 2 exists, and it can be demonstrated by any well-equipped audio lab, but there has been so little work done on it that we are here forced to concentrate most of our attention on number 1.
What we will do now is to place some limits on time delay or phase nonlinearity, then see what restrictions these limits indicate for tape recorder design.
=============

Table I
Some time constants of human hearing.
Acoustic Reflex (Gain Control) middle ear..... 10 mS
Gain Control-acoustic neurons (Brain) .... 20 mS
Time for wave to travel the length of the basilar membrane (inner ear) 5 mS
Time for a sound wave coming directly into one ear to diffract to the other ear (calculated) 0.7 mS
Refractory Period (dead time) of an acoustic nerve after firing 1 mS
Electrical pulse (spike) length-acoustic nerve. 0.5 mS
Pulse repetition time of acoustic nerve during onset of strong stimulation 1 mS
Limits of Precedence Effect'°:
Lower Limit 1 mS
Upper limit (limit of fusion)--clicks 5 mS
Upper limit (limit of fusion)--complex sounds .. 40 mS
=============

Fig. 2--The human ear, semi-schematic diagram.4-22.23 The ear consists of
three parts, an outer ear, a middle ear, and an inner ear. The outer ear (along
with the rotation of the head) assists in the perception of directionality
of the sounds. The external auditory canal is a Helmholtz resonator with a
resonant frequency of about 4 kHz. Due to the convolutions, the resonance is
strongly damped. The ossicles are an impedance matching system to couple the
air vibrations to the fluid in the inner ear. The impedance drops by a factor
of 22. The resonant frequency of the ossicles is about 1.7 kHz, and it is highly
damped. The inner ear is an acoustic transmission line with a low-pass characteristic
and a cutoff frequency of about 8 kHz. The cochlea cross-section shows how
the acoustic nerves connect to the hair cells. Relative movement between the
tectorial membrane and the basilar membrane disturbs the hairs, which sends
a signal via the acoustic nerves to the acoustic neurons in the brain.
=================

Table IV--Sources of amplitude and phase errors in magnetic recording.
Name of Error
Gap loss Spacing loss Thickness loss Head resonance Head core loss Azimuth error Gap scatter Faraday's emf Law Recording losses Signal demagnetization Gap length/coating thickness geometry Contour effect Equalization
Type of Error
Location of Error
Playback head Head/tape interface, on playback Tape, on playback Playback head Playback and record heads Between playback and record heads Record or playback heads Playback head Tape, on record Tape, after record
Record head, in conjunction with the tape Playback head contour/tape path geometry Record and playback electronics
Notes: A=amplitude, P=phase.
(1) Single-channel effect. Any single-channel effect can be a between-channel effect if the channels are different with respect to the effect.
(2) Between-channels effect.
(3) Sensitive to bias setting.
(4) As a function of frequency.
(5) As a function of wavelength, sensitive to head/ tape speed.
=================
Ears
Table I gives some time constants found in human hearing, and it is well to keep these constants in mind, since one would expect that any time constants of importance would be in the same range as these time constants of hearing. If time effects are described which are not in this range, one should suspect the reality of such effects unless they are satisfactorily explained.
Some description of these effects is in order. The ear consists of three parts (Fig. 2), an outer ear, open to the air and concluded with the membrane called the eardrum; a middle ear, consisting of three small bones (ossicles) suspended in muscle, which transmit the vibrations of the eardrum to another membrane, and the inner ear, which consists of a spiral fluid-filled chamber (cochlea) v ith a central (basilar ) mem [...] ments of the transport and heads are very critical, and mis-adjustments cause several kinds of losses and distortions. Tape magnetization is sensitive to temperature and mechanical stresses on the tape. The list goes on and on, and it's a wonder the process works at all but work it does and oftentimes very well.
There are a number of things in magnetic recording which cause amplitude losses. Some cause losses of only the amplitude of the signals, while others also cause phase changes.
Amplitude losses are very apparent to the listener, so Equalization in the playback and record electronics is utilized to compensate for the amplitude losses, and thus create a system which has a flat amplitude characteristic. The simplest type of equalization unfortunately creates additional phase changes in the system. These additional phase changes in many cases add to the phase changes already in the magnetic recording process, producing systems which are well-known for their inability to reproduce waveforms. " A list of the various losses is given in Table IV.
We'll take a closer look at these, and see how the phase distortion might be decreased by improved design.

Fig. 4 -- Schematic diagram of tapes with two signal tracks, passing playback
heads with gap scatter. A) Gaps parallel and aligned, but with between-track
phase or timing error. B) Same head, but misaligned so as to remove the between-track
phase or timing error.
Playback Losses (Mostly)
The first three sources of loss (Gap Loss, Spacing Loss, and Thickness Loss) are all amplitude-only loss sources on playback only and do not themselves have any associated phase changes. Gap loss is caused by the finite length of the playback head gap ("length" of a head gap is in the direction of tape travel, though the "width" of the head gap/track may be a much greater dimension). When the recorded wavelength is so small that the gap length is approximately equal to the wavelength, a null occurs in the output (see Fig. 8). There is a sharp drop from about the point where the gap is a half wavelength long to the first null (which occurs where the wavelength is about equal to one gap length). Spacing loss is due to the separation of the head from the tape and is 54.6 dB per wavelength of separation. Thickness loss is similar to a demagnetization loss. The signal on a tape may be viewed as a number of bar magnets laid end to end.
When the length of the bar magnets is long compared to their thickness (the tape coating thickness), all the flux lines from the magnets can enter the playback head. When the magnets are short compared to their thickness, some of the flux lines from the parts farthest from the head may not be able to enter the head and thus will be lost to the playback process. These losses may be kept to reasonable values by (respectively): (a) Using short-gap playback heads; (b) keeping the heads and tape surfaces very smooth and the head/ tape spacing small, and (c) designing tapes with thin coatings. These three dimensions are measured using the shortest wavelength to be recorded as the measuring unit. Modern systems, especially cassette systems, are designed with these three things in mind.
The next two, Head Resonance and Core Loss, are losses which are present in all heads, both playback and record.
Head resonance is caused by the inductance of the head winding in parallel with the distributed and stray capacitance. Core loss is caused by the fact that the magnetic permeability of the head material is a complex quantity which changes with frequency. With proper design and choice of magnetic material, these can be kept quite small, especially in the record head, which has to work with the high frequency bias signal. Resonance of the playback head has sometimes been used as part of the equalization, but modern practice is to locate the resonance above the audio pass band and utilize all-electronic equalization. This eliminates a large part of the phase shift problem before it ever gets started.
Azimuth Error and Gap Scatter are associated with the adjustment and precision of the head's manufacture. When more than one track is in use, it is impossible to adjust the head to eliminate these problems unless the head is perfectly made. Since nothing made by man is perfect, it is always possible to detect errors, even with the best heads available.

Fig. 5 -- Schematic diagrams of tapes with two signal tracks, passing playback
heads with gaps which are not parallel. A) Gaps aligned to give zero time error
between tracks. B) Azimuth aligned on one gap.
Azimuth is misaligned for the other gap, and a time error exists between the two tracks.
Of course, the best heads have acceptably small defects. Let's look at what is meant by these two terms.
Figure 3 shows a schematic of part of a tape passing a perfect two-channel playback head. We assume that the signal tracks have been laid down by perfect record heads, perfectly adjusted. By this, we mean that the record head gaps are perfectly straight and on the same straight line with each other, and that the angle between the gaps and the tape motion (called the azimuth) has been adjusted to be exactly 90°. Events which occur at the same time on both channels at record will play back on both channels simultaneously. Also note that the playback head is adjusted so that the gaps are exactly on top of the signal tracks. If the PB (playback) head overhangs the signal track, there will be loss of signal amplitude, but record heads are normally a little wider than PB heads to prevent this, so this particular error is not listed in Table IV.
Figure 4 shows the same situation, except that the PB head has gaps which do not lie on the same straight line, though they are parallel. Figure 4A shows the playback head aligned so that both gaps have their azimuth adjusted properly. The gap scatter is clearly seen. With the tape moving as shown, the gap on top will receive simultaneously recorded signals a little bit before the bottom gap will, thus introducing a time shift between channels. To stay within the first and second limits given in Table II, allowable gap scatter (which depends on head/tape speed) must stay within the limits given in Table III.
The limits in the third column, especially for the 1.875 ips tape speed (used for cassettes), are very demanding of the head-maker's art. The length of the cassette head gap (in the direction of tape movement, remember) is probably about 50 microinches or a bit less. To put this in perspective, green light has a wavelength of about 20 microinches. If you don't want to add to both stereo channels together to make one mono channel, the tolerance for time shift gives dimensions 10 times those shown for stereo channel addition.
Now we are talking about tolerances which any good head should meet, so that stereo image shift due to gap scatter should be relatively rare. Figure 4B shows a condition where the between-tracks time error has been adjusted away, but at the expense of misaligning the azimuth for both gaps (azimuth misadjustment causes an amplitude loss which increases for decreasing wavelength). Methods are in use for making either type of head azimuth adjustment. Both require the use of standard playback alignment tapes, available (at considerable cost) from several sources.

Table V--A Angle for 1-dB loss of signal at 15 kHz.
Table V--B "Gap scatter" caused by 1 dB of azimuth misadjustment at 15 kHz.
Figure 5 shows a similar situation, but the PB head has gaps which are not parallel. Figure 5A shows alignment such that there is no between-track time error. Figure 5B shows one gap with perfect azimuth alignment, which throws the other gap out of alignment by a serious amount. Proper adjustment for such a head is with the head aligned so that the loss due to misalignment of the azimuth is the same for both channels. 'There may be some residual between-track time error left after this type of adjustment, but it should not be serious.
Most real heads are of this type, but a good one will not require more than about Y to 1 dB of output drop in each channel at 15 kHz to make the compromise. Figure 5 is greatly exaggerated the actual angles are very small. Table VA shows just how small the angles were calculated to give a 1-dB loss in the 15-kHz signal due to azimuth misadjustment.
The angles are given in minutes and seconds (for those who have forgotten their geometry, 60 minutes = 1 degree and 60 seconds = 1 minute). If perfect heads have the azimuth deliberately misadjusted to give 1 dB of 15-kHz loss, this will cause an amount of "gap scatter" which is listed in Table VB. Comparing these figures with those given in Table Ill, we can see that these amounts of "gap scatter" will cause problems with adding stereo channels to form one mono channel, but are too small to cause audible stereo image shift. The track dimensions used in these calculations were taken from a convenient listing published by Nortronics," and the azimuth alignment loss calculations were made using the formula given by Begun:
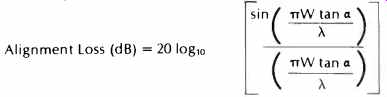
Where W is the track width, a is the azimuth angle (a=0 for perfect alignment), and X is `the wavelength of the signal (x=head/tape speed divided by the signal frequency). Faraday's emf Law says that the usual inductive PB head has an output proportional to the rate of change of the magnetic flux from the tape flowing in the head. The head output is not proportional to the level itself. The output from such a head has a constant (+ 90°) phase shift the same at all frequencies associated with it. The frequency sensitive amplitude loss (greatest at low frequencies) is normally compensated by an integrator in the playback electronics, which has an equal phase shift of the opposite sense (90°). The phase shifts cancel out, except at the ends of the compensation range. We'll come back to this when we cover equalization later.
Recording Losses
The category called "Recording Losses" is actually a collection of several kinds of signal losses which occur during the record process. These are due to 1b Bias Erasure, geometry of the record head field, recording field not aligned with the particles, Switching field not the same for all the particles, and recording not anhysteretic at high frequencies. All of these require some explanation.
Bias erasure is a description of the appearance of these losses. The bias for maximum sensitivity is not the same for short wavelength signals as for long. The bias is usually adjusted to optimize something such as sensitivity or linearity at long wavelengths, which means that the short wavelengths are overbiased and thus partially "erased." Actually, this "erasure" can be explained in terms of the next four loss sources.

Fig. 6 -- Section of the recording head and the tape showing the shape of
the recording field "bubble," the shape of the transition zone, and
the orientation of the magnetic particles in the tape. In this figure, the
record head gap length is of the same order of magnitude as the coating thickness.
The scale at the lower right shows the horizontal (above line) and vertical
(below line) field values at the points indicated. Note how the vertical field
falls off more slowly than the horizontal field as the tape moves away from
the record head gap.
The geometry of the record head field is shown in Fig. 6, which is a section through the record head and the tape. Inside of a half-cylindrical "bubble," which lies along the width of the record head gap, the particles in the tape coating are being magnetically switched (having their magnetization change direction) by the high-frequency bias. Outside the bubble, the bias field is too small to switch them. Recording thus takes place at the trailing edge of the bubble, in a transition zone. The reason that this zone is not infinitesimally thin is that all the particles do not have the same switching field, since they are not exactly identical.
Because of the influence of the larger vertical field near the head, the longitudinal extent of the transition zone is greater near the surface of the tape than it is half-way through the coating. The particles in the tape are normally oriented in the direction of head/tape movement and are thus easier to magnetize in that direction. Since the field at the surface is only partially longitudinal, it doesn't record on the surface particles as well as it does on the particles in the inner part of the coating. These things don't make much difference at long wavelengths, but at short wavelengths the strongest recorded signal is half way through the coating and not at the surface of the tape, so it suffers from spacing loss at playback. Note that the vertical component of the bias field cannot record upon horizontally oriented particles, but it can erase recording already done by the horizontal component of the field.
One might logically wonder why the acicular (needle-like) particles are used and why they are horizontally oriented.

Fig. 7 -- Tape flux amplitude circuiting the playback head at very long wavelengths,
such that the wavelengths are of the same order of magnitude as the overall
length of the head (not the head gap). 19 The interference effect is clearly
seen, as is the long wavelength cutoff.

Fig. 8 -- The total record/playback frequency characteristic before and after
the application of equalization to the record and playback circuits. The numbers
on the abscissa actually apply to the parameter g/X , where g is the playback
gap length and X is the wavelength. The frequency is given by f = s/ A , where
f is the frequency and s is the head/ tape speed, so the numbers on the abscissa
differ from the frequency only by a multiplying constant.
Acicular particles have a higher coercive force, which means that they are more resistant to demagnetization by external forces and internal fields. Orienting them lowers the distortion and increases the output and sensitivity at long wavelengths. It helps a bit at short wavelengths too, but not as much. Some tapes have a vertically oriented layer at the surface, which allows short wavelengths to be recorded right to the surface of the tape. This gets rid of the problem discussed in the previous paragraph, but brings up another: The vertical component of the field does not have a high gradient (drop of the field intensity as the tape leaves the gap) as does the horizontal component. This makes for a wide transition zone, unless a very short gap recording head is used. If the record head gap is too short, there will be difficulty in obtaining good long wavelength recording. The gradient of the horizontal field component is virtually unaffected by change of the record head gap length.
It has already been mentioned that the particles do not all have the same switching field. This means that the particles will "switch" or have their north- and south-seeking poles to exchange places at different applied fields. This causes the transition zone to be wider than it would be if all the switching fields were the same. This wider transition zone causes a smearing of the recorded signal, which blurs the short wavelengths more than it does the long, and results in further short wavelength loss.
To see why the loss of the anhysteretic quality of the recording (at high frequencies) is important, we must first see how anhysteretic recording works. The bias is a strong alternating field which carries the magnetization of almost all the particles through their major (magnetically saturated) hysteresis loop in a cyclic manner, i.e., the particles are magnetized to saturation first in one direction, then in the opposite one. The signal field is much smaller, a tenth of the bias field or less, and it is added to the bias field. When the tape moves out of the head field, the bias field dies out, and the particles stop switching, with some magnetized with their north poles in one direction, and some in the other. The number of left pointing particles is equal to the number of right-pointing particles with a no-signal condition, but the numbers become unequal as the signal strength rises, almost in perfect proportion to the signal strength. All this requires that the signal change very little as a section of tape moves through the transition zone. This is nearly true for low frequency (or long wavelength) signals, but becomes less true as the signal frequency gets higher (and the wavelength gets shorter). Thus, recording which is nearly anhysteretic at low frequencies becomes less so at high frequencies. Anhysteretic recording is the most efficient type of recording (i.e., it has the highest sensitivity), hence high frequency recording is less efficient than low frequency recording.
After the tape leaves the vicinity of the record gap, it still lies on the high permeability head for a while (permeability can be regarded as a measure of the affinity of a magnetic material for absorbing magnetic field lines). Recorded signals on the tape can be regarded as a series of small permanent magnets, which put out field lines. The head absorbs the field lines from these little magnets almost completely. This absorption of the field actually helps the magnets to retain their magnetization, as there is no field left to demagnetize them (any field from a permanent magnet always has the effect of demagnetizing the magnet to some extent). When the tape leaves the vicinity of the record head, the signals are demagnetized, with the shortest wave-length signals suffering the most. When the tape comes into contact with the playback head (which is also high permeability), some of the demagnetization is reversed, but some of it is not reversible and is permanent. Again, the short wavelength signals suffer in respect to the long wavelengths. Also, the tape with the highest permeability of its own suffers more from irreversible demagnetization than tapes with lower permeability.
Figure 6 shows a record gap which is of the same order of dimension as the coating thickness of the tape. If the record head gap is about twice as long as the coating thickness, this is a balanced situation, with neither the short wavelengths nor the long wavelengths being emphasized. If the record gap length is a lot smaller than the coating thickness, it is difficult for the head field to reach all the way through the coating. Recording tends to be near the surface, and short wavelengths are emphasized with respect to long. If the record head gap is quite long compared to the coating thickness, the field easily reaches all the way through the coating, but the field near the surface tends to be more vertical than horizontal at normal bias levels, the transition zone is correspondingly longer at the surface, and short wavelengths suffer more recording losses than long.
There is only a finite length of the playback head in contact with the tape. As the wavelengths begin to approach this dimension, an interference effect occurs. Some wavelengths cause more flux to go into the head than would go into an infinitely long head, while some wavelengths cause less. At wavelengths longer than about twice the length of the head, very little flux gets into the head, and the head is not responsive to longer wavelengths. The flux going into a head of finite length L is shown in Fig. 7 as a function of L/A where X is the wavelength (reference 19, page 181). The undulations are known in the trade as "head bumps." They can be minimized by contouring the head (thus, some writers call this "The Contour Effect") so that the tape approaches and leaves the head in a gradual manner. Any head, despite contouring, will have no useful output above some cutoff wavelength. This effect holds even for heads which are flux sensitive and suffer no losses from Faraday's emf Law. A flux sensitive head will read the tape flux at zero head/tape speed, and thus zero frequency, but it will not read tape flux at infinite wavelength.
Equalization
The total record/playback frequency characteristic before the application of any equalization is shown in Fig. 8. Also shown is the desired flat frequency characteristic after equalization. Some of the correction is done during recording, and some is done during playback. A considerable amount of literature has been written on just how much to apply in each case. The playback characteristics, being easiest to measure, are usually standardized to be less than the total amount needed for any tape. Only enough record equalization is applied to make the frequency characteristic flat with a particular tape; thus we say that a recorder is "optimized for a certain tape." With any other type of tape (which always has somewhat different characteristics), the overall frequency characteristic will not be flat.
The general type of equalization characteristics applied to the record and playback channels are shown in Fig. 9. A particular machine will sometimes leave out one or both of the shapes at the extreme ends of the record curve. Electronic circuits which have these frequency characteristics generally have an associated phase shift. When the curves change shape (as at the ends), the phase shift is especially pronounced. Because of the very complicated situation shown in Table IV, the phase shifts generated by the equalization never cancel the phase shifts arising from other sources. In fact, they sometimes add to them or create phase shifts where none were before.
In Fig. 9, one can estimate the phase shift caused by the two amplitude characteristics this way. If there is no slope to the amplitude characteristic, the phase shift is zero; if the line slopes to the right by 6 dB per octave, the phase shift is-90°, and if the line slopes to the left by 6 dB per octave, the slope is +90°. These relationships apply to a whole class of electrical networks called minimum phase networks. Most ordinary amplifier circuits and simple equalizer circuits fall into this category. With some effort, the designer can construct circuits which have phase shift different from the rules given above. He can then (theoretically) tailor in a phase shift characteristic which exactly compensates for the total of the phase shifts from all other sources, and get a tape recorder with á flat phase shift characteristic. Such a recorder would not suffer from waveform distortion, group delay, or any of the other ills previously outlined. For several reasons, this is not what is presently being done.

Fig. 9 -- The general frequency characteristic of the playback and the record
equalization for audio machines. The numbers above the curves give the amount
of phase shift at those points, if the equalization is produced by minimum
phase networks.
Phase Compensation
An excellent example of the current practice is the Ampex ATR-100, a mastering recorder with phase equalization as well as amplitude equalization. 14.2° For all of the errors listed in Table IV except "Faraday's emf Law" and "Equalization," the designers used only a careful and thoughtful engineering design to keep the phase errors suitably low. This design ensured that the major part of the phase shift error would be in the equalization. A standard playback equalization was used to compensate for the Faraday's emf Law. This introduced an extra phase error in the manner which has been described. Then, in the record electronics, an extra phase shift was introduced in the opposite direction which compensated for the phase shift errors in all of the equalization. The phase shift adjusts along with the amplitude adjustment, so that compensation is obtained for any tape to which the machine is adjusted. Thus, tapes made on this machine will play back on any other machine with small phase errors, since the compensation is recorded onto the tape itself. A square wave recorded on this machine comes back looking very much like a square wave something many other machines will not accomplish.
Another example, the Sony 880-2, utilized a different design philosophy. Again, careful engineering design and some carefully made heads keep the introduced phase shift down to a low level. Contrary to the Ampex practice they chose to put their phase equalization in the playback circuit. So long as both recording and playback is done on the same machine, it makes little difference where the phase equalization is, provided the recordings are at a suitably low level.
When the recordings are at levels near saturation, phase shift can cause higher than usual peak factors (the ratio of the peak value of a waveform to its rms value) to occur. If these peaks are high enough to be clipped by tape saturation or by the electronics, audible distortion will occur. Clearly, it would be much better to correct some of the phase distortion in playback and some in record, 21 to keep the peak factors down to a suitably low level. Sony's engineers probably chose to do it all in playback since any machine sold to the general public will presumably be used to play quite a few tapes made on other machines. The Sony machine will perform phase correction on "prerecorded" tapes.
Now let's take this to its ultimate conclusion. Suppose that all the recorded tape producers use machines with complete phase compensation on all their record circuits. These tapes will play back on all the old machines free of phase distortions. On your brand-new machine with phase compensation in the playback circuits (Sony isn't the only one!), the tape will be overcompensated and will be phase distorted in the opposite sense. Plainly, someone out there ought to be doing some work on standardization of phase correction techniques. Since there still is an argument raging on whether phase compensation is necessary or not, there's not much chance of standardization right now.
None of the foregoing should be construed as a criticism of the engineering decisions which have been made so far. In the absence of standards, all the decisions have been about as good as could be made.
Conclusions
This discussion has looked at a number of different aspects of the audio phase problem. I think that a good case has been made that phase distortions are audible and that phase corrections will result in cleaner sound. We have looked at the sources of phase distortions in magnetic recording, and some of the means now being used to correct for those phase distortions. Lastly, we have seen that there is a great need for standardization in phase correction (phase equalization) techniques right now! Standardization people, what are you doing for us?
References
1. H. L. F. Helmholtz, On the Sensations of Tone, translated by A. J. Ellis in 1885 (from the third German edition, 1870), Dover, N.Y. 1954, p. 127.
2. Thomas A. Saponas, Randolph C. Matson, and J. Robert Ashley, "Plain and Fancy Test Signals for Music Reproduction Systems," I. Audio Eng. Soc., Vol. 19, No. 4, April, 1971, pp. 294-305.
3. Benjamin B. Bauer, "Audibility of Phase Distortion," Wireless World, Vol. 80, No. 1459, March, 1974, pp. 27-28.
4. Manfred R. Schroeder, "Models of Hearing," Proc. IEEE, Vol. 63, No. 9, September, 1975, pp. 1332-1350.
5. James Moir, "Phase and Sound Quality," Wireless World, Vol. 82, No.1483, March, 1976, pp. 80-84.
6. D. Preis, "Linear Distortion," /. Audio Eng. Soc., Vol. 24, No. 5, June, 1976, pp. 346-367.
7. Takeshi K. Matsudaira and Takeshi Fukami, "Phase Difference and Sound Image Location," /. Audio Eng. Soc., Vol. 21, No. 10, December, 1973, pp. 792797. Also correction, ibid, Vol. 22, No. 2, April, 1974, p. 186.
8. D. E. L. Shorter, H. D. Harwood, and W. I. Manson, "Stereophony: The Effect of Interchannel Differences in the Phase/Frequency and Amplitude/Frequency Characteristics," BBC Engineering Monograph No. 56, December, 1964, 27 pages.
9. Villy Hansen and Erik Rorbaek Madsen, "On Aural Phase Detection," J. Audio Eng. Soc., Vol. 22, No. 1, January-February, 1974, pp. 10-14.
10. Hans Wallach, Edwin B. Newman and Mark R. Rosenzweig, "The Precedence Effect in Sound Localization," American I. Psychology LXIII, pp. 315-336. Reprinted in /. Audio Eng. Soc., Vol. 21, No. 10, Dec. 1973, pp. 817-826.
11. John K. Hilliard, "Notes on How Phase and Delay Distortions Affect the Quality of Speech, Music and Sound Effects," IEEE Trans Audio, Vol. AU12, No. 2, March-April, 1964, pp. 23-25.
12. Benjamin B. Bauer, "Some Techniques Toward Better Stereophonic Perspective," J. Audio Eng. Soc., Vol. 17, No. 4, August, 1969, pp. 410-415. Reprinted from IEEE Trans. Audio, Vol. AU-11, May-June, 1963, p. 88.
13. Duane H. Cooper and Takeo Shiga, "Discrete-Matrix Multichannel Stereo," /. Audio Eng. Soc., Vol. 20, No. 5, June, 1972, pp. 346-360.
14. Alastair M. Heaslett, "Phase Distortion in Audio Magnetic Recording," paper presented at the Audio Eng. Society 55th Convention, Oct. 29- Nov. 1, 1976. AES Preprint No. 1178 (P-3), 14 pages.
15. Jim Grimshaw, "Multi-Track Phasing Errors," db Magazine, Vol. 9, No. 11, Nov., 1975, pp. 40-42.
16. C. D. Mee, The Physics of Magnetic Recording, North-Holland Pub. Co., Amsterdam (1968). Distributed in the U.S. and Canada by Interscience Publishers.
17. Design Data, Nortronics Audio Heads; Nortronics Track Configurations; from "Nortronics Audio Magnetic Heads Application Notes and Design Data," Nortronics, 1975 (Form 9223).
18. S. J. Begun, Magnetic Recording. Rinehart & Co., Inc., New York, 1949.
19. W. K. Westmijze, "Studies on Magnetic Recording," Philips Res. Repts. 8; April, 1953, pp. 148-157; June, 1953, pp. 161-183; August, 1953, pp. 244-269; October, 1953, pp. 344-346.
20. Larry Zide, "The Making of the Ampex ATR-100," db Magazine, Vol. 10, No. 12, Dec., 1976, pp. 32-35; and Part II, ibid, Vol. 11, No. 2, Feb., 1977, pp. 3638.
21. Finn Jorgensen, "Phase Equalization is Important," Electronic Industries, Oct., 1961.
22. Arthur C. Guyton, M.D., Textbook of Medical Physiology, second ed., W. B. Saunders, Philadelphia, 1961.
23. William D. Zoethout and W. W. Tuttle, Textbook of Physiology, eleventh ed., C. V. Mosby, St. Louis, 1952.
Also see: Catastrophe Theory and its Effect on Audio (Part II) (Apr. 1979)
Influence of Listening Rooms On Loudspeaker Systems by Roy F. Allison (Aug. 1979)
Build a Headphone Amp by Walter G. Jung (May 1979)
(Source: Audio magazine, April 1979)
= = = =

