|
|
I can remember walking across Manhattan on a sparkling day in the late summer of 1996 to hear a then-new digital coding system called Direct Stream Digital (DSD). The venue was Sony Music’s West 57th Street studios; I had barely an inkling of what I was in for. Sitting in the control room, I could see a jazz trio in the next studio, everyone close-miked. On the other side of the console was a pair of Wilson Audio Watt/Puppies. The idea was to compare the sound of the console feed with the sound through a then-state-of-the-art 20-bit pulse-code modulation (PCM) chain and the sound through a DSD chain, and then to decide which of the latter was closer to the former. As I recall, we had a choice of 48- or 96-kHz sampling rate on the PCM system, and a Studer 15/30-ips deck was available to play analog masters.
Everyone seemed to agree that DSD was closer to the direct feed than 48-kHz PCM, but something stuck in my craw. Finally, the light dawned. In the next room, I could see a microphone positioned 3 inches in front of the trumpet and another swallowed up in the piano, but my ears heard a reasonably spacious sound with a modest degree of ambience. When I pushed the point, the engineers admitted to adding a bit of reverb and otherwise toying around to make the sound “more natural.” Presumably, this was done digitally. Whether this affected the experiment’s validity is moot, but, having run lots of demos in my 10 years at CBS Labs, I am a very suspicious guy. So I left Sony Music that day unconvinced that DSD was better than PCM. Besides, DSD proved to be a real bit-hog compared with PCM, and the scientist in me thinks that wasting resources is a sign of inelegant engineering.
We asked whether Sony intended DSD as a new consumer audio format and got the ol’ runaround: “DSD was developed to archive Sony Music’s vast collection of analog masters that are drying out and disintegrating this very moment!” (Help! Help!) Sony’s stated DSD objective was a digital recording system that would pre serve every nuance recorded on those masters, was not limited by PCM’s bandwidth and dynamic range constraints, and was convertible to any PCM format presently used or likely to be used, without sound degradation. Phew! Such a lofty objective, and here I was quibbling about bit rate! For shame. Besides, videotape (the proposed archiving medium) can Store wads of data, Sony pointed out. I repressed my urge to ask why one would want to replace one crumbling tape medium with an other when optical storage is possible and left the studio.
If DSD is the perfect way to archive past recordings, ipso facto it must be the best way to record new programs. Soon after, Sony and co-developer Philips trotted the DSD system around the pro audio world to drum up interest.
Despite a lack of professional mixing and sound processing equipment capable of handling DSD (DSD signals can’t be mixed on a PCM board), Sony managed to convert a handful of top-notch recording engineers, who made some excellent recordings using the new DSD technology. I remained my curmudgeonly skeptical self until last January, when I heard these recordings in a private demo at the Consumer Electronics Show. They’d now become Su per Audio Compact Discs (SACDs), and a new consumer audio format was born.
Sony and Philips have been accused of launching SACD simply to roil the waters for DVD-Audio, a statement easier to make than to prove. The way I see it—and I’m sure I’ll get lots of arguments on this—DVD-Audio extends present-day PCM technology into the surround sound realm and permits use of higher sampling rates and longer word lengths, whereas SACD takes a fresh look at what digital recording should be all about. DVD-Audio’s goals are admirable—but it is still a multibit, PCM system, whereas SACD uses the aforementioned Direct Stream Digital technology. Whether DSD proves sonically superior to 20-bit/192-kHz PCM remains to be seen, but I’d not rule out the possibility. (Yes, I know DVD-Audio claims to permit 24-bit resolution, but for the reasons given in my DVD-Audio article in the September issue, I think that’s just specsmanship.)
It’s not what DSD has, but what it doesn’t have, that makes the difference: a case where less may be more and where 1 bit may be better than 20. Nor did DSD emerge from the seashell as a fully formed Aphrodite. DSD is a byproduct of developments that led to the modern PCM converter. In fact, DSD analog-to-digital converters and most modern high-resolution PCM A/D converters start off the same way. Both use high-speed, oversampling 1-bit (or “low-bit”) delta-sigma modulation, and noise shaping, to transform analog signals into the digital domain. DSD samples incoming signals 2,822,400 times a second (64 times the 44.1-kHz CD rate), an over-sampling rate typical of PCM converters as well. (For more about oversampling, 1-bit delta-sigma modulation, and noise shaping, see “A Compleat Digital Primer.”) Where DSD and PCM part company is in what they do with the 1-bit data stream.
To record PCM, the high- speed, 1-bit data are converted into multi-bit words at a lower sampling rate. In the conversion, data are decimated and digitally filtered to avoid aliasing (see “Primer”), because the sampling rate is being reduced. Although a brick-wall digital filter is easier to implement than its analog equivalent—it simply involves a series of mathematical calculations—its effects are not necessarily benign.
Digital filters overshoot and ring both before and after transients, and each mathematical calculation increases the word length. If the accumulators in the filter cannot accommodate the longer words, overshoots caused by the calculation can be clipped or the least significant bits (LSBs) of calculated data can be truncated. In a complex, multistage brick-wall decimation filter, internal word length can reach or exceed 100 bits! To constrain the word length, well-designed multistage decimation filters re-quantize (to reduce the word length) at each stage. In any case, the output data must be requantized to fit the system parameters—i.e., word length must be reduced to 16 bits for CD or to 16, 20, or 24 bits for DVD-Audio. Each requantization produces distortion if the data are not properly redithered, but in randomizing quantization distortion, dither raises the noise floor slightly. No free lunch!
When played back through a delta-sigma D/A converter (the dominant method nowadays), multibit PCM words are converted back to a high-speed 1-bit (or low-bit) data stream by an interpolation filter and returned to analog by a delta-sigma modulator and reconstruction filter—hence more calculations, more overshoot, and more phase shift. Which perhaps is what has led some audiophiles to prefer the sound of gentle, low-order interpolation filters to that of brick-wall types, despite the large amounts of aliasing distortion that so-called soft filters permit! I’m not in that camp, but it does raise a question: Why use this approach? The simple answer is that delta-sigma modulators have been found to be the most practical and cost-effective way to convert digital information back to the analog domain. A 1-bit modulator is inherently linear and, properly implemented, can have wide dynamic range. Ladder DACs have problems achieving 16-bit accuracy, never mind 20 or 24 bits!
The beauty of a 1-bit delta-sigma-modulated data stream is that it contains the analog signal within itself. Although the delta-sigma stream is digital, in that it toggles between two fixed levels (“1” and “0”) rather than trying to describe a continuum of intermediate values, Fourier analysis of the data stream reveals the original analog signal embedded in the original band of frequencies where it began. All that is needed to restore it is an analog low-pass filter to dump the digital trash!
The salient difference between Direct Stream Digital and PCM is that DSD cuts out the middlemen. Instead of using a decimator and digital filter to get 1-bit data into multibit form for recording and then using more calculations in the player to turn PCM words into 1-bit equivalents so they can be linearly converted to analog, DSD records and plays the 1-bit stream directly (Fig. 1). In principle, all that is needed in the player is an analog low-pass filter to reconstruct the audio and reject the ultrasonic digital trash. Looked at this way, DSD is a simpler, more straightforward, more analog approach to digital recording, and the old audiophile adage that says “the less the better” is more often right than wrong.
DSD also offers a flexible trade-off between bandwidth and dynamic range. With PCM, bandwidth is sharply limited to half the sampling rate while maximum dynamic range is dictated by word length. Proponents argue that the dynamic range of a PCM system can be made arbitrarily large by increasing the word length, but in my experience, the practical end-to-end limit for a PCM system is about 20 bits, and there are good reasons for that.
With DSD, bandwidth and dynamic range are determined by the type and order of the noise shaping used in recording and, to a lesser extent, by the analog low-pass filter in the player, characteristics that are not cast in stone. The only constraint the SACD “Scarlet Book” of standards places on the encoder is that the total noise energy in the region below 100 kHz not exceed -20 dBFS. There is a recommendation that SACD players incorporate a 50-kHz low-pass filter “for use with conventional speakers and amplifiers,” but higher cutoff frequencies are permitted.
High-order noise shaping forces more of the quantization noise into the ultrasonic region and improves dynamic range within the audio band. But since high-order noise shapers are not stable when overloaded, they must be designed with controls that prevent overload and a way out should it occur. (The same applies to the noise shapers used in high-resolution PCM converters.) The cutoff frequency of the noise shaper enters the equation be cause it affects the bandwidth of the DSD system. You could, for instance, use a high cutoff frequency to maximize system band width, in which case you’d have the choice of using either high- order noise shaping to maintain the same dynamic range over the wider bandwidth or a lower-order filter at the sacrifice of dynamic range. On the other hand, you also could lower the cutoff frequency of the noise shaper to improve dynamic range in the audio band (for a given filter order) if you thought that delivered better sound.
The point is that DSD is a flexible coding system that leaves the recording engineer (and A/D converter designer) in charge of sound quality. I find that appealing because it portends future quality improvements within the SACD format. By adopting 16-bit/44.1-kHz PCM, Sony and Philips locked the CD in a straitjacket. Apparently, they don’t intend to repeat that situation. The flip side of the flexibility coin is that it’s difficult to speak in concrete terms of a player’s (or the SACD format’s) bandwidth or dynamic range because the two are interrelated and affected by choices made in the recording studio.
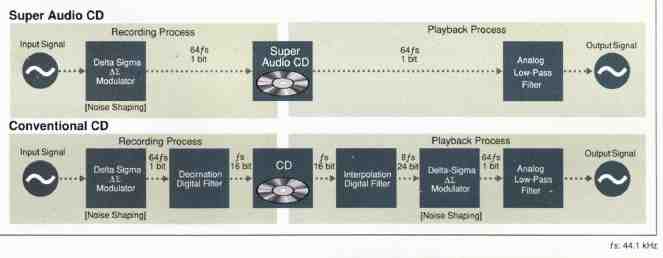
Fig. 1—By eliminating the conversions from delta-sigma modulation to PCM—and
back—that are typical of modern CD recording and reproduction, SACD greatly
simplifies the entire process.
Suffice to say that SACD claims the equivalent of 20-bit PCM resolution within the audible range and a bandwidth of 100 kHz. That should encompass the range of human hearing quite nicely. Presumably the 20-bitll00-kHz claim is based on using reasonably high-order noise shaping in the A/D converter and a fairly steep low-pass filter in the player. There’s a limit to how far one can (or should) go in optimizing both factors at the same time. It is counterproductive to shoot for maximum bandwidth together with maximum dynamic range. Doing so would require a very high- order noise shaper with a very high cutoff frequency, which would force so much of the quantization noise into the ultrasonic region that a brick-wall filter would be required in the player to dump it. That's exactly what DSD was meant to avoid.
So much for DSD; what about SACD? I draw a distinction be tween DSD, the recording technology, and SACD, the consumer audio super-disc, because DSD may succeed for archival purposes whether or not SACD proves a consumer success. Physically, an SACD is very similar to a DVD. Although it can't be played on to day's DVD players, I see no reason why it couldn't be played on fu ture systems because the physical size (12 centimeters), storage capacity (4.7 gigabytes per layer), and optimum laser wavelength (650 nanometers) are the same. (In fact, Philips recently announced its intention to deliver a universal DVD-Video/DVD-Audio/SACD/CD player late next year.) Only the maximum transfer rate and data format differ, SACD discs are single-sided and come in three varieties: a disc with one high-density (HD) layer that carries DSD information exclusively, a disc with two HD layers that provides 8.5 gigabytes of storage for longer playing time, and a hybrid that has an HD up per layer and a 44.l-kHz, 16-bit Red Book (CD-compatible) lower layer that existing CD players should recognize (Fig. 2). Hybrid discs solve the dual-inventory problem that was said to be so important to the music industry. At one point, a DVD-Audio spokesman told me that the same could be done with their format, but lately they seem to be backing off that position on the grounds that they've found many CD players that will not recognize the CD layer of a hybrid disc.
===

Fig. 2-A hybrid SACD has two layers. The high- density layer is derived from
DVD optical technology and carries the high-resolution DSD data streams. The
base layer is essentially a standard CD. The HD layer is only semi-reflective,
to allow the longer wavelengths of a standard CD player's laser pickup to penetrate
it and read the CD layer.
====
Four of the five discs I got with the Sony SCD-1 (reviewed else where in this issue) were hybrids, so I thought I'd give them a go on the players I had around. All played fine on my reference Sony CDP-XA7ES player, on a Technics portable, and on an antediluvian Yamaha CD deck. My Sony DVP-S7700 DVD player had no difficulty recognizing the hybrid SACD as a CD, nor did my Philips laserdisc player. The only machine that refused to read the disc was a Matsushita-sourced single-laser DVD player that also burps on CD-Rs.
SACD supports 255 tracks, which eliminates any need for index numbers. It also supports text (song. lyrics, liner notes, and the like), graphics, and limited video (still-frame, album covers, etc.), but it is not primarily a video system. The format allows for as many as six channels of DSD surround sound in addition to a DSD stereo track. SACD does not incorporate anything like DVD-Audio's Smart Contents automated-mix-down capability; so a separate stereo track is not merely an option if high-resolution stereo is de sired, but a necessity. Sony and Philips contend (and most top notch recording engineers would agree) that it is not possible to do justice to stereo by having a player generate it from a surround mix, even if the producer has as much control over the mix-down process as he does in Smart Contents. In the studio, stereo mixes are made from the original multitrack master, not from a surround mix thereof. Sometimes even the microphone setup is different for stereo than for surround sound.
SACD was designed to have the same 74-minute playing time as a normal CD (sensible in light of the Red Book layer on the hybrid disc), but with eight DSD channels (six surround plus studio mixed stereo) on the HD layer, SACD devours storage capacity at a wild pace. The DSD data rate comes to 2.8224 megabytes/second, which chews up a 4.7-gigabyte HD layer in 27 minutes, 45 seconds. To boost this capacity to 74-minutes, the Philips half of the team concocted a lossless compression algorithm called Direct Stream Transfer (DST). DST uses a combination of linear prediction and Huffman coding to compress the data by a ratio greater than 2:1. (By my calculations, they'd need 2.67:1 packing to deliver 74 minutes of six surround plus two stereo channels on a 4.7-gigabyte layer.)
DST divides the data into 13.3-millisecond frames. Within each frame, a linear filter predicts whether the next bit will be "1" or "0," based on the value of the preceding bit. The predicted value is compared with the true value. If the prediction is correct, the comparator outputs a "0"; if it's incorrect, the comparator outputs a "1." Because audio data are not random, the predictor is right more often than wrong. Therefore, the output of the comparator is likely to consist of relatively long strings of "0s" with occasional "is" where the prediction was incorrect. And because it contains long strings of the same value, the predicted data is more redundant than the original. The redundancy is then removed by a Huffman code, which produces the actual compression.
Huffman coding replaces common patterns of data with simpler codes. For example, if four consecutive "0s" is the most frequent occurrence, "0000" could be replaced with a single "0," defined in the Huffman table as "0000." That yields 4:1 compression for the "0000" pattern, but now a different code is needed to replace a single "0." Because the single "0" code will be more than 1 bit long, some ground is lost. The point is to make the data as redundant as possible (via linear prediction) and then assign the shortest codes to the most common patterns and the longer codes to the least common patterns, A Huffman table can be fixed or computed for each data frame to optimize compression on a frame-by-frame basis. It's not clear which approach is taken, though I suspect Philips derives a new table for each frame based on the patterns found within it.
Because the table constantly changes in this case, modifications to it must be included with the data as side information, so the player knows how to decipher the block. Consequently, there's a delicate trade-off between the size of the frame and the amount of side information that must be transferred to optimize the compression ratio.
Assuming error-free transmission, this type of compression is lossless. That is, the original 1-bit data stream can be perfectly re stored from the compressed information. Although I use the term "prediction error," there is no error overall. When the encoding predictor is wrong, that information is sent in the data to the player whose decoding predictor is told "whatever you think the value should be is wrong, so fix it!" As I write this, the only SACD player and existing sample discs are stereo-only. One cannot help but conclude that in order to beat DVD-Audio to market, choices had to be made. My guess is that Philips' DST algorithm was not locked in silicon in time, but it's also possible that no multichannel DSD masters were available. As I said earlier, DSD cannot be mixed on a PCM board, and DSD mixers and signal processors are as rare as hens' teeth.
Sony has stated that the SACD launch will be supported by an initial release of approximately 40 titles from AudioQuest, Delos, dmp, Mobile Fidelity, Telarc, Water Lily Acoustics, and Sony Music. Sony Music has indicated it will release 10 titles per month there after. Time will tell. Philips can't help because it sold its record labels (PolyGram et al.) to Universal Music, which is aligned with the DVD-Audio group. At present, the DVD-Audio group has gotten more companies to sign on the dotted line than have Philips and Sony, possibly because it seems more amenable to the stronger copy-protection and anti-piracy schemes the record industry de sires. But the protection issue remains a thorn in the sides of both camps.
As I see it, the music industry wants something it can't have without destroying the rationale for a superior audio carrier. From what I've been told, the record companies not only want to be able to protect against indiscriminate digital cloning but to control copying in the analog domain as well. It's one thing to scramble a digital signal or insert flags in the data stream that le gal digital recorders recognize and refuse to record; it's another to have protection carry over into analog output signals. Digital flags can be recognized, acted upon, and stripped before conversion to analog, but it seems to me that anything that ends up recognizable by an analog recorder can't help but be audible. If the music industry couldn't get away with this on CDs (it tried, remember), how can it possibly expect to do so on a higher-quality medium? I think the best the record labels can hope for is to make indiscriminate digital cloning illegal and difficult and let it go at that. No one is seriously proposing military-style encryption, and anything short of that will quickly be hacked by commercial pirates. Commercial piracy and the Internet are the serious threats to the music industry, not audiophiles. We're the customers! Actually, SACD seems to have certain advantages over DVD-Audio with respect to piracy, even though Sony and Philips won't agree to any tampering with the signal that possibly could be audible. SACD discs not only carry a digital watermark but can also carry a visible one. As with DVD-Audio, the digital watermark can be used to prevent a player from reproducing an illegal disc and to control how many copies can be made. The (optional) visible watermark assures the buyer that the disc is legal.
The visible watermark is created by Pit Signal Processing (PSP) while mastering the disc. PSP varies the pit width in a way that leaves a visible pattern on the disc-for example, the DSD logo. Reportedly, the technology needed to do this in a way that does not cause jitter is extremely complex, and the magic boxes will be made available only to licensed pressing plants. PSP offers a fighting chance of reducing commercial piracy if consumers refuse to buy unwatermarked discs. But that's a big if, when visible watermarking is optional. A
I wish to acknowledge the assistance of David Kawakami of Sony and Dr. Andrew Demery of Philips in providing AES Preprints and other technical background material. Special thanks to Ed Meitner of EMM Labs for sharing his experience in designing the DSD professional equipment that made possible many of the recordings I heard.
=== A COMPLEAT DIGITAL PRIMER ===
Digital audio systems have two things in common: sampling the analog input signal at a regular rate and quantizing (assigning a value to) each sample. The sampling rate puts an upper limit on frequency response; quantization establishes the dynamic range. The theoretical upper limit of a sampling system is one-half the sampling rate. This is the so-called Nyquist cri tenon. Because Compact Discs use 44.1-kl4z sampling, the theoretical upper limit on frequency response is 22.05 kHz.
Signals of higher frequency that enter the sampler cause aliases that cannot be distinguished from real signals. Aliasing is a form of intermodulation distortion, or beating between the signal and the carrier, that produces new signals at the sum and difference frequencies. For example, if a 43. l-kHz (or 45.1-kHz) signal is sampled at 44.1 kHz, a 1-kHz beat is produced that cannot be distinguished from a true 1-kHz signal.
Aliases at the sum frequencies (87.2 kHz and 89.2 kHz in this case) also occur, but, lying in the ultrasonic region, they are in audible. The 1-kHz difference signal definitely is audible, so signals of frequencies greater than half the sampling rate must be prevented from entering a sampler. This is the job of the anti-aliasing filter.
In digital audio's early days, anti-aliasing filters were complex analog circuits that attempted flat response to 20 kHz and high rejection at 22.05 kHz and above. Designing such a filter was (and is) a formidable task; building an affordable one was (and is) even more difficult. In-band response seldom was flat, out-of-band rejection rarely was as much as needed, and group delay wasn't uniform. This caused severe phase distortion at high frequencies.
Oversampling-sampling at a higher rate than the Nyquist criterion requires for the desired bandwidth-offers an out.
Instead of sampling at 44.1 kHz, suppose one samples at 176.4 khz (4x oversampling) while maintaining the original 20-kHz system bandwidth. Signals above 88.2 kHz still alias, but the lowest frequency that creates a sub-20-kHz alias is 56.4 kHz (176.4 kHz minus 156.4 kHz equals 20 kHz). That provides more room for the analog input filter to work, greatly simplifies the design, and improves phase response.
When the digital signal is returned to the analog domain, it appears as a series of samples, and similar aliasing problems occur. If the D/A converter operates at the original sampling rate, another brick-wall filter is needed at the output. (That's what was done in the early days, and CDs got the rap for bad sound.) A solution is the use of another form of oversampling, a digital interpolation filter.
Interpolation filters use mathematical calculation to increase the sampling rate and move images out to higher frequencies, where they can be removed by a relatively simple analog filter. Over sampling is beneficial but has a major drawback: There's less time for each conversion, which is a real problem if one is shooting for 16-bit (or better) accuracy. This brings up the subject of quantization.
Just as prices are usually rounded up or down to the nearest penny because that's the smallest coin in our currency system, a digital representation must be rounded up or down to the nearest value permitted. This produces quantization error, which in the audio world is called quantization noise. PCM 16- bit binary words (CD, DAT, etc.) have 2^16 possible values. In decimal notation, that's 65,536 possible values, one of which is zero. Because the maximum quantization error is always ±½ of the least significant bit (LSB), increasing the word length provides finer resolution and better dynamic range. In a PCM system, theoretical signal-to-noise ratio is equal to 6.02 times the number of bits plus 1.76 dB, so a 16-bit system can theoretically handle a dynamic range of 98 dB. Achieving this in practice is easier said than done.
Early analog-to-digital and digital-to-analog converters used a straightforward way of converting between domains. On the AID side, the sample value was compared to a set of voltages established by a resistor network. The digital word was then generated by successively approximating the value until it got as close as possible. On the D/A side, another resistive ladder generated currents proportional to each bit of the digital word. The currents corresponding to the "1" bits were summed to pro duce the output. The concept is simple, the execution excruciating. The problem is one of tolerance; the MSB (most significant bit) of a PCM word accounts for half the total value, and it's nearly impossible to make it precise enough that the error doesn't swamp the less significant bits. Consequently, early 16- bit converters rarely achieved true 16-bit performance.
Most modern converters use high-order oversampling, I-bit or low-bit delta-sigma modulation, and noise shaping to transform between the domains. Delta-sigma modulation is an offshoot of the delta modulator developed at Bell Labs decades ago. Delta modulators are rather simple circuits that compare the present value of the analog signal with the past and output a "1" if the value has in creased and a "0" if it has decreased. Delta modulators do not encode the actual signal; instead, they mathematically encode its change-its delta, or derivative. By including an integrator (sigma) in the comparator loop, the delta modulator becomes a delta-sigma (probably more properly called a sigma-delta) modulator. Integration mathematically reverses the derivative so that a delta-sigma modulator encodes the signal itself.
In theory, a 1-bit delta-sigma modulator is perfectly linear, because all bits have identical value. The problem is quantization noise. With only 1 bit to describe data, the dynamic range is zilch! Oversampling and noise shaping came to the rescue. Digital quantization noise spreads from DC to half of the sampling rate. (See Fig. A1.) With 64- or 128-times oversampling, most noise is in the ultrasonic region and can be disregarded, but the raw quantization noise of a 1-bit converter is so great that oversampling by itself is not enough. Doubling the sampling rate spreads the noise over twice as much bandwidth, but that improves the dynamic range within the audio band by only 3 dB. Thus, 64-times oversampling results in an 18-dB gain and a 1-bit, 64-times oversampled converter has about 4 bits of resolution in the audio band. Hardly enough! Here's where noise shaping comes in. Noise shaping is a technique that effectively low-pass filters the desired signal and high-pass filters the quantization noise. This squeezes the noise out of the audio band into the ultrasonic region, much as air in a cylindrical balloon can be squeezed into one end by grabbing the other (Fig. A2). Actually, a 1-bit delta-sigma modulator is itself a first-order noise shaper. The integration provides the filtering action, and a 64-times oversampled delta-sigma converter has better than 4-bit resolution within the audio band.
Combining several delta-sigma modulators in the same loop results in higher-order noise shaping that forces more of the noise into the ultrasonic region. Within reason, this technique can achieve arbitrarily good resolution within the audio band and perfect conversion linearity. The extremely high sampling rate also effectively eliminates aliasing concerns in the delta-sigma modulator, although aliasing can occur if the 1-bit stream is down-converted into multibit PCM at a slower rate. One of DSD's prime claims to fame is that it avoids that last step.
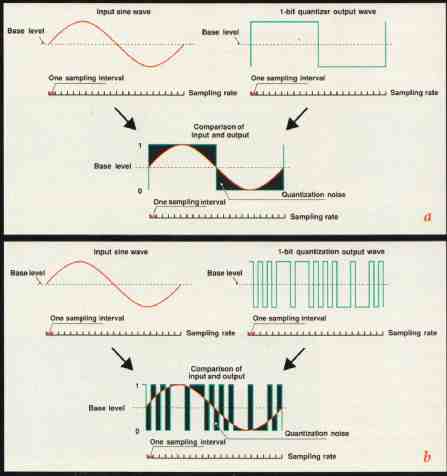
Fig. A1. A simple 1-bit PCM quantizer (a) produces very high quantization noise
(the difference between the input and output waveforms) within the audio band.
A 1-bit delta-sigma modulator (b) produces the same total amount of quantization
noise, but it is spread over a much wider bandwidth, so less of it appears
in the audible range.
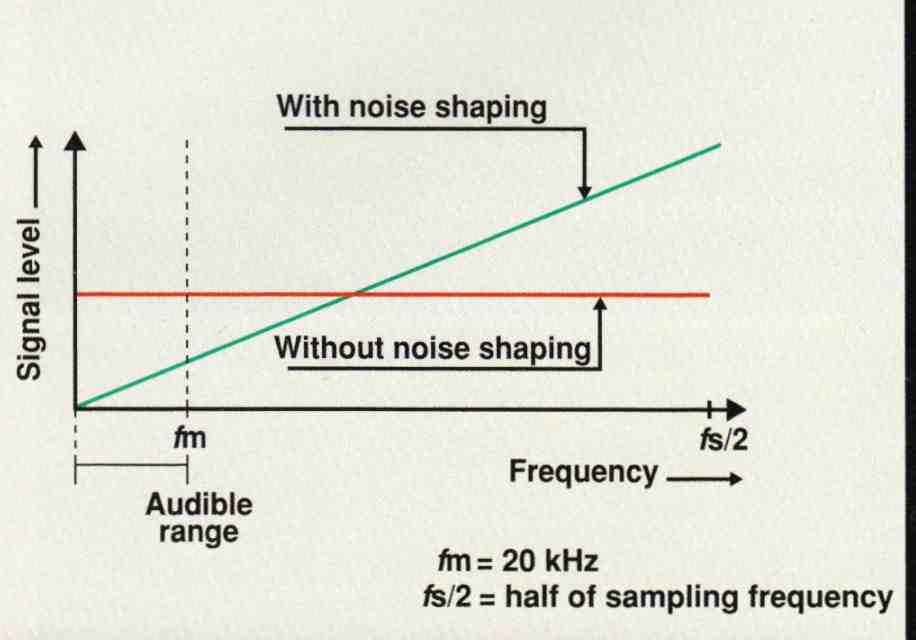
Fig. A2.Comparison of noise spectra with and without noise shaping.