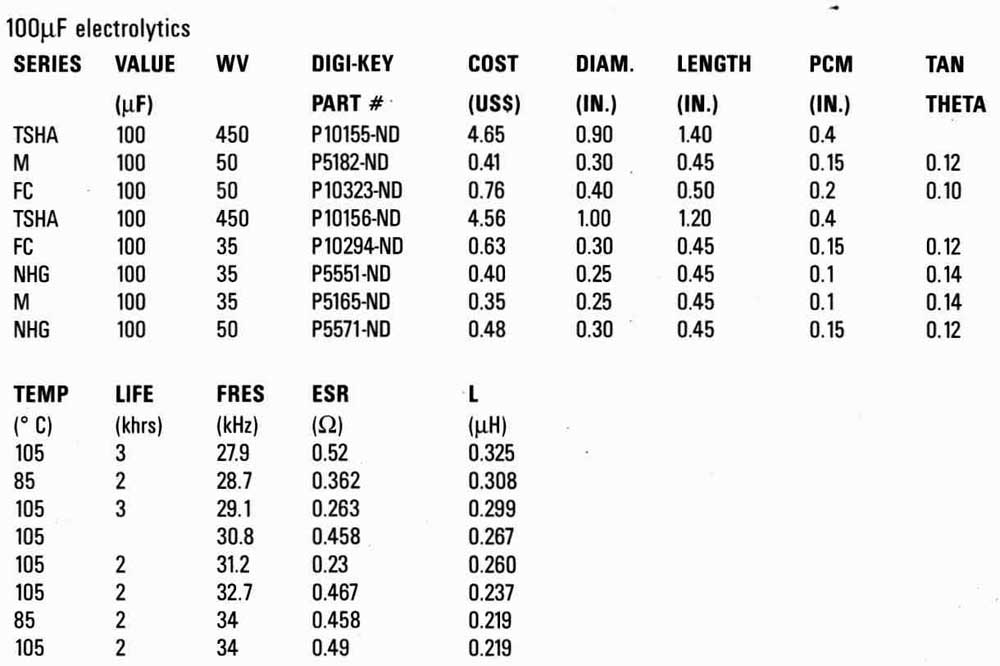
 TABLE 1A
TABLE 1A | Home | Audio mag. | Stereo Review mag. | High Fidelity mag. | AE/AA mag. |
A closer look at the role of capacitors in power-supply design and bypassing electrolytic caps with small film caps to improve their performance.
It’s almost axiomatic among designers of audiophile projects and products that electrolytic capacitors should be bypassed with smaller, high-grade film capacitors. In the course of planning some preamp projects, it occurred to me that, like most people, I wasn’t approaching the matter scientifically. Instead, when designing a power supply, I threw in what seemed like the right size electrolytic, stuck in the biggest bypass caps that would fit the board and budget, and turned my attention elsewhere.
However, after a couple of bad experiences (they mostly involved opamps going ballistically unstable), I decided that electrolytics and the film caps that bypass them deserved a closer look. I was curious how some popular, widely available capacitors actually behaved when tested in the crucible of life itself, to borrow a cliché. How, in particular, did they act at high frequencies? What were the design implications of that behavior?
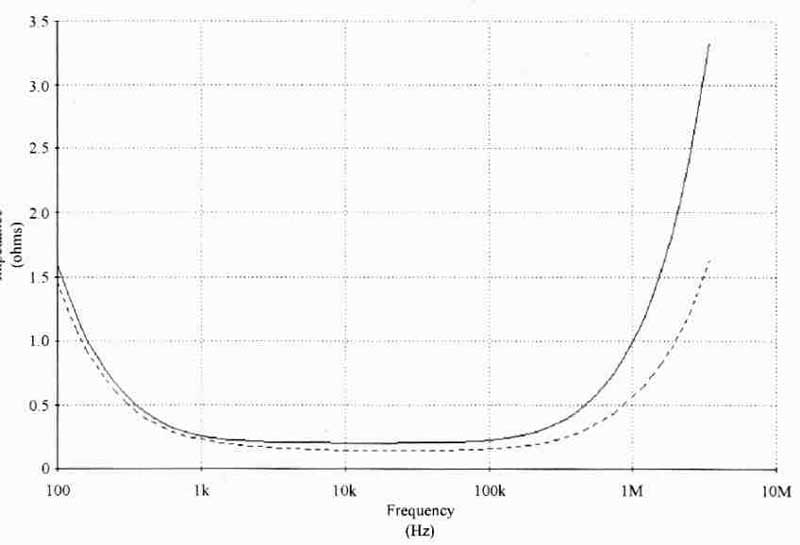
Figure 1: typical capacitor impedance curve. The solid line is a single 1000uF
35v NHG -series electrolytic, unbypassed. The dashed line is the same capacitor,
but by passed with a 0.1 uF 400v polypropylene and a 100uF 50v NHG-series electrolytic.
WHAT’S IN A CAPACITOR?
Theoretically; a capacitor is nothing but a pair of plates with a dielectric material between them—a device that holds an electric charge that can pass alternating current but not direct current. A pure capacitor contains nothing but capacitance.
Real-world capacitors, however, include ‘parasitic elements produced by physical construction of the device. First and foremost, inductance (L) which resonate with capacitance to produce an impedance curve such as in Fig 1. At low frequencies, including the ones you typically want to filter out of a power supply; the capacitor acts like a capacitor its impedance decreases as the frequency goes up. This is the capacitative region.
At higher frequencies, the impedance levels off, then begins going up with increasing frequency, as inherent inductance takes over. This is, logically enough, the inductive region. Meanwhile, at the resonance frequency, the impedance does not drop to zero, as it would with a perfect capacitor and inductor. In stead, there is some residual impedance, which is known as the equivalent series resistance (usually abbreviated ESR).
A real-world capacitor can, therefore, be represented by three components in series (Fig. 2).
There are other parasitic elements as well, most notably a network representing a phenomenon called “dielectric absorption” and a resistor representing leakage current, but I’ll save those for another time.
WHAT IS IT FOR, ANYWAY?
Most of the time, we use electrolytic capacitors in electronic audio projects for two purposes: filtering ripple and other noise out of power supplies, and bypassing voltage regulators. (They’re some times used as audio coupling caps too, but we never do that, right? In any case, that’s also a topic for another time.)
Arguably, the most important role electrolytics play in our designs is filtering raw supplies. With the typical full-wave rectifier, this ripple is at 100 or 120Hz, depending where in the world you live. If you’re using a half-wave rectifier, the ripple will be 50 or 60Hz.
The caps have more to do, though. 8th- con diodes ring as they switch the current on and off;’ this radio-frequency ringing can propagate through the audio system, perhaps causing intermodulation distortion and other ill effects. Power-supply caps can help shunt this high-frequency energy away from audio circuits--if they have a low-enough impedance at high frequencies. (It’s best, of course, if you generate as little high-frequency crud as possible; to this end, fast, soft-switching diodes and perhaps snubber circuits sup ply the requisite ounce of prevention.)
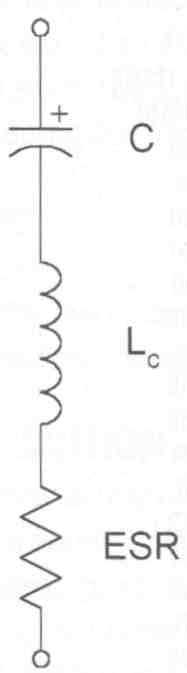
Figure 2: simplified equivalent circuit for real-world electrolytic capacitor.
Not shown: additional elements representing leakage current and dielectric
absorption.
Supply capacitors can help filter out radio-frequency interference (RFI) that sneaks into the system by various routes, including the umbilicus connecting a main chassis to a separate supply box.
We also use electrolytic capacitors in voltage-regulator circuits. Typically, integrated-circuit regulators require a certain amount of capacitance at the output for stability. Adjustable regulators also need capacitors shunting the voltage-set ting resistor, to minimize both noise and output impedance. Complex regulators, such as the Sulzer or Jung circuits, use electrolytics in several places, including the outputs, feedback networks, and reference voltage sources.
In short (well, in shunt), electrolytic capacitors and their behavior are central to the job of designing power supplies and the regulators they feed.
I decided to buy a pile of capacitors and see what they did.
EXPERIMENTAL DESIGN
For the most part, I limited my study to capacitors that are easy to obtain, al most anywhere in the world. That meant Panasonic electrolytics, made by the giant and multinational Matsushita Corp., and available in the U.S. from Digi-Key Electronics (www.digikey.com) as well as many other suppliers. I ordered caps in common sizes, increasing roughly geometrically (100uF, 330uF, 1000uF, 3300uF), and in common low voltages (35, 50, and a few 100v units), plus a couple of high-voltage devices suitable for tube designs. For bypass caps, I mostly stuck with polypropylenes from Panasonic, plus a selection of B&C units and a couple of miscellaneous polypropylene, ceramic disc, and tantalum caps from my parts drawers.
My test hookup is shown in Fig. 3. I connected a GW GAG-808A audio generator to a non-inductive 820-ohm resistor, which fed the device under test (DUT). (I soldered a clip-lead directly to the business end of the resistor to minimize the effect of stray inductance.) I measured the voltage across the DUT with a Hewlett-Packard 400H AC voltmeter, clipping its input leads directly over the leads feeding the DUT.
I calibrated the whole setup by inserting a 10-ohm resistor as the DUT and setting the oscillator so that the meter read full-scale (on the 0 - 10 scale, al though the actual sensitivity was 30mV) at 1kHz. This enabled me to read impedances directly without calculations.
Once I was calibrated, I measured each capacitor by twiddling the oscillator dial until I found the resonant frequency, where the impedance dipped to its lowest level. (This often required looking at the meter’s needle with a magnifying glass to catch its small movements near the minimum point.) I then recorded the frequency and impedance. Knowing the frequency and the capacitance of the DUT, I calculated the inductance on a spreadsheet, using the formula:
L = 1/4π2 fres2 C
…where fres is the resonant frequency in Hz and C is the capacitor’s value in farads.
WORDS OF CAUTION!
It’s worth noting a few caveats and limitations in this experiment. For the lowest impedances, particularly with the 3300uF caps, I was working dose to the noise-limited resolution of the system. That means that the impedance figures for those caps should be taken with several grains of salt; I think the data reliably ranks which devices have higher or lower impedances, but the absolute ESR levels for these caps may be off. This doesn’t affect the actual frequencies of resonance, though, from which I calculated the inductances.
I was curious to see whether the electrolytics’ behavior would change when the capacitors were charged and the dielectrics were “formed.” Accordingly, I jury-rigged a setup to charge the DUT from my 15V bench supply via a 10k resistor, and measured its resonant frequency and ESR cold (never charged) a minute or so after turn-on and again an hour after turn-on.
For the two caps on which I tried this, the result was straightforward: no change at all in the resonance characteristics, either in frequency or ESR. (There was, however, a big change in leakage current, as measured by voltage drop across the 10k resistor, after the system had been on for an hour. Those folks who tell you to let your gear warm up for a while before you listen aren’t just whistling Dixie.)
Be warned, though: I made this comparison on only two capacitors out of the several dozen in the stack. While I can’t see any reason why the rest of them should behave differently, I admit that I took the easy route and didn’t try. Instead, I did all of my tests with the capacitors cold and unused.
As I took my measurements, I entered them into the spreadsheet, along with various specs gleaned from the manufacturers’ datasheets, since I wanted to see whether any of them correlated with the results of my tests.
RAW RESULTS
The test data is summarized in Table 1a (included here). Each group of capacitors is ranked by increasing resonance frequency (corresponding to decreasing inductance). Looking at the data, several things jump out.
1. I had rather expected the low-ESR electrolytics (FC series) to have lower inductance than their higher-ESR counterparts, and thus lower impedance at high frequencies. They didn’t.
2. I had similarly expected that, within a given series, capacitors with higher working voltages would have lower inductance, lower ESR, or both. Mostly, they didn’t.
3. Looking at correlations between published specs and measurements, I found few. The specs for tan theta seemed to be only weakly correlated with measured ESR. There was no apparent correlation between inductance and price. On the other hand, there did seem to be a connection between inductance and size: the lower-inductance caps within a group of electrolytics had shorter bodies. (Makes sense.)
4. Among electrolytics, the larger the cap’s value, the lower the resonant frequency. For example, the highest f_res among the 330uF caps was lower than the lowest one among the 100uF. (The high-voltage devices were an exception; they really should be considered separately.)
5. I expected the one Multicap I had in the group, which is advertised as having a “self-bypassed” construction, to behave differently from a more conventional cap of the same value. It didn’t.
6. I expected the small-value film capacitors I tested to have extremely low ESRs. They didn’t.
7. Finally, it was clear that if you want a capacitor that remains capacitative be yond 1MHz, you should probably look at a ceramic disc or tantalum device. (OK, that’s r really news. Nice to find data that confirms received wisdom, though.)
SIMULATIONS AND COMBINATIONS
What does all this information mean?
And how does it relate to our stated topic, bypassing?
To find out, I ran simulations pairing likely-looking capacitors, using the venerable ECAP program available as shareware from cdquickcache.com/pcecap.htm. I won’t bore you with all of the results (if you’re hungry to see them, I’ve posted them as a .txt file at audioXpress .com, but I’ve summarized one set of comparisons in Table 2).
This table shows a couple of promising 1000uF electrolytics, paired with popular 0.1 and 0.47uF film caps, along with various other bypasses that came out well in the raw tests. I compared the lowest-inductance electrolytic (from the NHG series) with the lowest-ESR cap (Ft series), looking particularly at behavior up in the Mhz region. This is a critical area for filtering out diode switching noise and RFI, not to mention possible decoupling of wideband opamps. Again, a few findings stand out:
1. The low-ESR FC caps inevitably had higher impedances at 1MHz and 10MHz, with a given bypass cap, than the lower inductance NHG caps. This pattern held in every value of electrolytic I tested.
2. In general, using single bypass caps, the 0.47uF cap provided lower impedances at 1MHz than the 0.1 at 10MHz, though, the 01uF cap was usually lower. Using the 1.0uF B&C metalized cap provided slightly lower impedances at both frequencies. (It’s nice and small, which often means lower inductance.)
3. Adding a third cap further improved performance. The 10uF GE polypropylene cap, which I obtained as surplus from Madisound a few years ago, had a distinctly salutary effect: high-frequency impedance was significantly lower with it than without it. (This may be a finding of marginal usefulness, though, as these capacitors have vanished from the market, and I haven’t found another tubular unit with similar characteristics.)
Similarly good results could be obtained by making the third cap a 100uF NHG series electrolytic. Patching in a small tantalum device lowered high-frequency impedance still further. Variety in this context, seems to be the spice of life.
HAVE YOUR CAKE AND EAT IT TOO?
My tests imply a distinct trade-off in capacitor choice: For a given value of capacitance, you can design for the lowest possible ESR, or for the lowest possible impedance at high frequencies. Is it possible to get both at once?
For this test, I compared a 3300uF low ESR capacitor from the Ft series with a composite unit made up of three 1000uF NHG-series caps, connected in parallel.
Each was bypassed in various ways.
The composite cap produced an ESR that was about 40% that of the bypassed 3300uF cap, at a higher frequency; while its impedance at 1MHz and 10MHz was less than one-third of the larger unit’s. Clearly, you can get the best of both worlds; as many designers have found, several little guys can outperform one big one—if your space and cash budgets don’t mind.
It’s been suggested—indeed, it’s a common belief among designers--that parallel capacitors produce “multiple resonances,” or a single resonance with a sharp peak where the inductance of the large capacitor resonates with the capacitance of the small one. In my situations, I did not find this to be the case. The main reason is the high ESR of the small film capacitors; if I change the simulated ESR of the small cap to 0.1-Ohm, a peak does appear. With the actual ESR’s of these capacitors, how ever, the curve is smooth, as shown in the dashed line of Fig 1.
A HIGH-VOLTAGE INTERLUDE
For these experiments, I concentrated on lower-voltage capacitors, mostly because the projects I’m working on now happen to be op-amp based. However, I also design tubed circuits, which deserve at least a passing glance. Table 4 on shows a few simulations I ran using high-voltage capacitors. And, while I’m at it, Table 5 shows the high-frequency performance of the various bypasses by themselves.
DOWN TO EARTH
What do all these tests and data imply for our designs? I think a few conclusions can be drawn.
1. For a given application, you really need to run the calculations for the particular capacitors you’re considering. If you simply plug in a randomly chosen electrolytic and whatever film cap seems inviting, you’re likely to get less-than- optimal results (and you may spend more money than necessary). The tests aren’t hard to do, and of course I’ve generated some numbers that you can use.
2. Don’t assume! The results of combining capacitors are sometimes counter- intuitive, and you can’t know until you try (or at least simulate).
3. Smaller caps, in multiples, may out perform their larger brethren.
4. Finally the old and unfashionable ceramic disc cap has its place, particularly when you’re trying to filter out radio-frequency crud.
MAKING CHOICES
It’s worth remembering, as I rattle on about comparative impedances, that there are other important criteria to look at when picking capacitors for a design Temperature rating can be important -- particularly in a box with limited ventilation—and projected lifetime is often an issue. When picking the first capacitor after a diode bridge, leakage current and ripple-current rating may be important. So may cost and size.
Electronic design is a balancing act; a good designer is always weighing one factor against another, knowing that it’s impossible to optimize everything at once. I hope I’ve given you some information in this article that can help you juggle your way to better results.
REFERENCES
1. Jim Hagerman, Calculating Optimum Snub bars,’ Audio Electronics January 1998. p. 26.
2. Michael Sulzer, A High Quality Voltage Regulator fur Operational Amplifier Preamplifiers.’ Audio Amateur 2/1998, p. 8.
3. Walt Jung, Regulators for High-Performance Audio. Audio Amateur March 1995 and June 1995.
= = = =
Prev. | Next |