Are cathode followers poorly suited to driving capacitive loads in comparison to common cathode amplifiers? The answer may surprise you.
I was flipping through some old audio magazines and was surprised to discover that it has been over 20 years since I presented the then as-yet-to-be-named “Mu Follower” circuit in the pages of The Audio Amateur. A quick Google search of the phrase revealed ongoing interest in the circuit, from audiophiles presenting and discussing what they’ve built to advertisements for commercial products that feature it. People have made many modifications including using different triodes for the top and bottom tubes and even replacing the top tube with a pentode!
Like any circuit, however, it has its limitations and has attracted its share of criticisms. Probably the predominant criticism relates to the fact that its output is essentially a cathode follower (CF). And we all know how poorly those circuits drive capacitive loads, right? I mean, the CF tube actually disconnects from the load on the negative stroke, doesn’t it?
This belief in the unsuitability of the CF for driving capacitive loads is wide spread. Even a well-regarded web-published reference on tube design actually shows a schematic with a CF output line stage that sports a graphic of a bomb with a lit fuse!
But how bad is it in actuality? I’ve never encountered an attempt to quantify this problem, yet I’ve always wondered about it myself So I thought I’d take a stab at it.
THE CF INDICTMENT
As I understand it, the basic concern is as follows. A line stage output swings over the range of several volts. If it’s a cathode follower, its grid swings over approximately the same range as its cathode (actually, a little more). If the cathode is coupled to ground through a capacitor and if the grid drops far enough quickly enough, the cathode may fail to keep up with the grid and the tube might completely stop conducting current. Then the only thing that can pull the output down is the cathode bias resistor, a weak passive device that is not up to the task of pre venting distortion because it can’t change the capacitor voltage quickly enough.

FIG. 1: The common-cathode amplifier on the left is the “equivalent counterpart”
of the cathode follower on the right.
This is thought not to be the case with the common-cathode amplifier (CCA). With the load capacitor connecting the plate to ground instead of the cathode, the grid can swing as quickly as it likes and the cathode will tend to follow it; there is no capacitor to prevent the cathode from doing so. Even if there is a cathode decoupling capacitor, the signal on the grid is usually much smaller than that at the output because of the gain of the amplifier. The grid simply doesn’t travel far enough to bias the tube off, or so goes the argument.
To determine the validity of this point of view, you must take a quantitative in stead of a qualitative tack. You need to propose and run a test in which you can subject a CF and its equivalent CCA counterpart (whatever that means) to the same challenging loads and compare their performances.
DESIGNING THE TEST
First, consider the question of what “equivalent counterpart” CCAs and CFs would look like. I would argue that circuits using the same triode type biased to identical plate voltages and currents and having identical static and dynamic load lines would fit the bill. A suitable pair might employ 6DJSs set for 100V and 10mA. The CCA would have its grid biased to 0V DC, a cathode resistor of 200-ohm, and a 20K-ohm plate resistor connected to a 300V DC supply.
The CF would be constructed by swapping the CCA plate and cathode resistances, maintaining the 300V plate supply and biasing the CF grid to about 200V DC. 6.3V DC heater supplies would be tied to each cathode. A large coupling capacitor would connect the outputs to a ground-referenced capacitive load. I chose a 3.3uF capacitor I had handy for output coupling.
You need to define a capacitive load. For a long time, 1nF was considered to be a standard for a severe load provided by a line stage cable. You could argue this choice, but it seems a reasonable first selection; I’ll get to more severe loads later on.
In parallel with 1nF, place a 100k-ohm resistor that represents what might appear at the input of a tube power amp. Figure 1 shows the completed CF and CCA circuits.
Now you need to choose a load signal. Audio signals are band-limited, so it is unreasonable to employ, say, a square wave at the stage inputs. A sine wave should do. You’ll need a high audio frequency and level to get a large slew rate and to allow the capacitor to present the biggest drive challenge. I think 2V RMS is a reasonable choice for an output at line levels; any higher and just about any power amplifier is going to experience more problems than the line stage driving it. (Of course, to establish identical output load levels, the AC signals at the grids of these two circuits will differ to compensate for differing circuit gains.)
For a frequency, let’s get silly and choose 20kHz. I hope no one really expects to be dealing with a signal like this and that if they do, they will at least concede that signal levels fall off at more than 6dB per octave above this frequency. That means the load will still demand the highest peak current at 20kHz.
With circuit details, load, frequency, and signal level defined, you should check the dynamic load line on the plate curves for any problems before you actually perform the test. From Figure 2, (which shows this load line), note first that the circuits are not making any significant deviations from the zero signal operating point—the signal varies by only a few volts and less than .5mA out of the available 10. So don’t expect any gross distortion, “disconnection from the load,” or “failure to follow” the signal applied to the grid.
Second—and here’s what’s really interesting—did anybody notice that I didn’t mention circuit topology? This dynamic load line should apply to both the CF and the CCA, suggesting that you should expect similar performances from the two circuits.
TEST MEASUREMENTS
Sure enough, when you build and test the circuits, your expectations are borne out. Neither circuit exhibits any visible misbehavior, as you can see in Figs. 3 and 4. It looks as though you’ll need to work harder to get the CF at least to grossly distort.


FIG. 2: Load line (full scale and zoom) of CF and CCA with 1nF load capacitances
(plate and curves shown are approximations only).

FIG. 3: CCA output with a load
capacitance of 1nF; FIG. 4: CF output with a load capacitance of 1nF.

FIG. 5: Load line of CF and CCA with 22nF load capacitances (plate curves
shown are approximations only); FIG. 6: CCA output with a load capacitance
of 22nF.
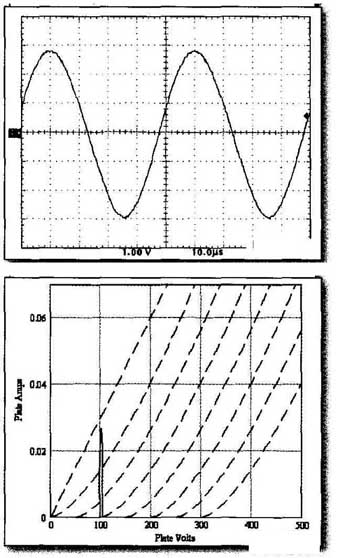
FIG. 7: CF output with a load capacitance of 22nF; FIG. 8: Load line of CF and
CCA with 7nF load capacitances (plate curves shown are approximations only).
Back to the load line examination then. Increase the value of load capacitance to 22nF. Figure 5 shows that although there is much more variation in plate current, in neither circuit should the tube shut off I'm sure that distortion has risen significantly, because the tubes are now operating within the compressed portion of the plate curves, but neither tube should yet be disconnecting from the load. The test results of Figs. 6 and 7 bear this out. At 22nF, the CF still refuses to disconnect or to behave any worse than the CCA.
I needed to increase the load capacitor to 47nF before the load line in Fig. 8 would predict a problem. Under these conditions, the tube was being called on to pass a negative plate current, something that it clearly should not be able to do and that should result in gross distortion. You should expect problems with both the CF and the CCA with this load.
The measurement of Fig. 9 finally shows the kind of expected gross distortion. The CF signal follows almost a straight line in traversing from the highest to the lowest voltage, and that “fall time” is much longer than the gently curved, sine-like rising transition. Here you can see the CF disconnect from its load.

FIG. 9: CF output with a load capacitance of 47nF.
During the fall time, the signal is con trolled solely by the nearly constant cur rent passing through the 20K cathode resistor. That current is approximately 10mA, the quiescent bias current of the 6DJ8. When passed through a 47nF capacitor, it should produce a voltage slew rate of 10mA/47nF = 2V/10 This, indeed, is what you see on the scope.
Surprisingly, the measurement of Fig. 10 shows the opposite problem with the CCA—it disconnects on the rising edge! The two signals appear almost as inversions of one another. Each circuit has run out of current under exactly the same load and drive conditions. Figure 11 shows what happens at the CCA grid, plate, and cathode, and may help you get a better idea of what occurs in both circuits under these conditions.
Why do such different circuits per form so similarly? Well, if you require a certain voltage across a given load, then you establish the need for a particular current. That means that the triode in each circuit must supply that current out of its plate and cathode.
The identical voltage drops across the same passive impedances in each circuit force the triodes to support identical voltages equal to the differences between the 300V supply and the voltages across the passives. This renders the load lines in each circuit identical, and when placed on top of a set of plate curves, this means that identical values of control voltage (Er) appear for each triode. No wonder the CF and CCA behave the same in this test!
If you’re still having trouble coming to grips with this equivalence, consider that the active portion of the triode is just a controlled current source in parallel with a resistance—the same current that goes in one end comes out the other. From an AC point of view, the plate and cathode are indistinguishable apart from a signal inversion—until you remember that the magnitude of the source’s current is con trolled by the difference in voltage be tween the cathode and grid and cathode, and not grid and plate.

FIG. 10: CCA output with a load capacitance of 47nF.
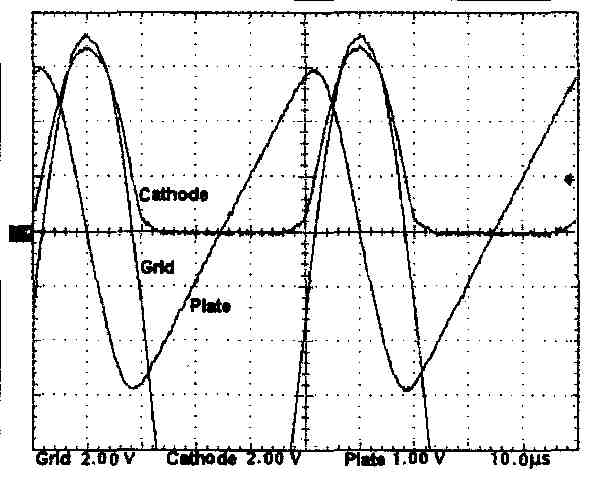
FIG. 11: CCCA signals with a load capacitance of 47nF
ANOTHER QUESTION
So equivalent CCAs and CFs perform the same into capacitive loads?
Well, yes. That is, if you’re looking only at distortion. But what about frequency response? Here the CF actually has an edge over the CCA.
The output impedance of this CF is around 100-ohm, giving a 0.1dB break point of 80kHz into a 1nF load. But the CCA’s output impedance of about 20K || ( = 30) * (200 + 100) C = 6200 gives a 0.1dB breakpoint of 1300Hz. Even if you completely bypass its 200-ohm cathode resistor with a capacitor to get a plate impedance of 2600-ohm, the 0.1dB breakpoint rises to only 3100Hz. Certainly not audio-grade performance!
To flatten out the response and form an acceptable line driver, the CCA must be placed within a feedback loop to lower its effective output impedance. The CF has no such limitation. You have a choice of whether or not to use a CF within a feedback loop.
A COMPOUND DRIVER (CD)
Although it would seem that the CF and CCA are up to the tasks of driving any load seen within or by a preamp or line stage, other applications such as driving a headphone directly might make you wish for a driver that excels in both sourcing and sinking current. The obvious next step is to combine the advantages of both circuits by stacking a CF on top of a CCA as shown in Fig. 12. This is nothing new and has been done extensively in the past.
I have chosen to retain the previous operating points, although the opportunity exists in this stage to reduce bias currents and improve efficiency. Operation at reduced bias might have come at the cost of increased low-level distortion due to de scent into the more compressed portions of the plate curves.
One of the goals of this circuit is to apply drive signals that are identical in magnitude, but opposed in phase, between the grid and cathode of each of the two triodes. Matching the magnitudes ensures a proper balance in the two sections, and of course the phase inversion is necessary for the proper operation of the driver.
All this is accomplished with the transistor phase splitter. Purists may gasp in dismay at the intrusion of transistors into hallowed thermionic ground, but this component is there because it forms a simple circuit that is visibly (on the scope, at least) linear over the fill range of operation until it cuts off, from delivering the maximum drive to the CCA to doing so for the CF. I chose this in favor of a triode; I did not want the nonlinear plate curves of a triode phase splitter near its point of cutoff to cloud the operation of the driver.
Another point should be made about the CD as well as the CF and CCA: none of the triodes in these circuits can be driven to pull grid current during the application of steady-state sine waves. The three capacitively coupled grids prohibit this; if they were to draw a current on positive peaks, a DC voltage would be established across the capacitors which would re-bias the grids to a point just below that required for grid current to flow.
As for the CF triode in the CD, you can see that the current flowing through the resistor between its cathode and grid into Q2 can flow only in a direction that prevents its grid from being more positive than its cathode, thereby precluding grid current. This establishes a convenient maximum current, common reference point for the purposes of comparing all stages.
So how does the CD drive a 47nF capacitor? Very well, as you can see in Fig. 13. Figure 14 shows that it also does well with a 100nF capacitor (although there is a little compression of the signal at the peaks and troughs). This is a good thing; it needs to do better than twice as well as two CFs or CCAs, or else you would just parallel a pair of those two circuits and avoid the complexities of the CD’s phase splitter!
The explanation for this superior drive capability is evident from a glance at the 6DJ8 plate curves. For a peak current drive of Ec = 0V and Ep = 100V, 40mA of plate current can be had! Of course, you wouldn’t want to bias a triode anywhere near that point, or else you’d exceed the power ratings for the tube and burn it out.
One other point should be noted. Be cause of the positive feedback from the CD’s CF’s cathode to its grid through the 2K resistor, the CD’S output impedance is much higher than that of a CF. In fact, it is closer to that of a CCA. You could easily see this by finding what value of resistive load placed at the CD’S output would cut the output signal level in half So like the CCA, the CD would need to be enclosed in a feedback loop to have a low enough impedance to drive a 1nF capacitive load over the full audio bandwidth.

FIG. 13: CD output with a load capacitance of 47nF. FIG. 14: CD output with a
load capacitance of 100nF.
PRACTICAL CONSIDERATIONS
For all three of these circuits—and, in fact, for just about any topology—it is al ways wise to insert a resistor whose value is commensurate with the required frequency response between the stage out put and a capacitive load. Such a resistor can help to prevent oscillation (especially when inter-stage feedback is involved) and provides some limit on the current being called for in the case of unexpected high frequencies such as RF interference. This can have the salutary effect of reducing distortion within the system as a whole. This wasn’t done in the circuits presented here because I wanted to let the load capacitors do their worst.
BACK TO THE Mu FOLLOWER
Please excuse me for returning to this subject, but it’s my involvement with this circuit that got me to do the research for this article in the first place. I hope I’ve addressed the concerns of those of you who mistrusted both CFs in general and the use of one in this circuit in particular. I would like to ask the audio community for a favor. I very much doubt that I was the first to discover the combination of low distortion/high gain (~ mu) low output impedance (~1/gm) and high power supply rejection (~ mu) that this relatively simple circuit has to offer” Does anyone have an earlier reference to a discussion of the characteristics of this topology? Please, no SRPPs! This circuit may have its own charms, but none of them are among those cited above for MFs. The “SRPP” dates from US patent 2,310,342 issued in 1943, which, by the way, mentioned neither the acronym SRPP nor any term that gave rise to it. (Anyone know where that came from?)
CONCLUSION
I’ve shown both by experiment and by explanation that a cathode follower can drive a capacitive load just as well as an identically biased common-cathode amplifier. The CF, in fact, has an edge over the CCA in that its lower output impedance can drive a 1nF cable with a flat frequency response over the audio range without re course to enclosure within a feedback loop.
I trust that I identified and addressed the concerns that people had about CFs driving capacitive loads. If you think I’ve missed something or just flat out disagree with what I’ve written here, let’s hear about it in the DIYAudio.com forum!
REFERENCES
1. Christopher Paul, Letters to the Editor, TAA 2/85, p. 51.
2. Christopher Paul, Letters to the Editor, TAA.4 3/91, p. 43.
