By Forest H. Belt, CET

------ A communications technician is shown checking the noise-cancellation
of a business-radio transceiver.
For servicing many electronic products, recurrent-sweep 5-MHz scopes are totally obsolete. Even ordinary triggered scopes are barely adequate for some tasks. The proper analysis of defects in today’s sophisticated electronic products demands the use of wideband triggered oscilloscopes. Here are suggestions for obtaining helpful waveforms, measuring the parameters, and interpreting those characteristics related to bandwidth.
Two examples
A communications technician recently repaired a business-radio transceiver. According to the customer's report the noise-blanker switch didn't eliminate the ignition noise. It might have been a difficult diagnosis. But it wasn't because the tech was equipped to solve it.
First, the technician connected his noise generator to the radio and verified that the noise-blanker function was not working. Then with his scope, he began tracing noise pulses through the blanker stages. These were discrete stages (not inside an integrated circuit), and that made the tracing easier. Quickly, he located the bad stage, and found a leaky capacitor in a pulse-forming network near the blanker output.
Knowledge and equipment--Two factors helped the technician solve this service problem quickly and profitably. First, he understands the operation and" testing of noise blankers. Second, he uses a wide band triggered scope. The scope revealed a badly distorted waveform of the blanking pulses. Even mild ignition noise wasn't cancelled by the degraded pulses.
Viewing digital pulses--In another example, a digitally-controlled tuner was not working properly. Channel numbers appeared on the screen as they should, but the raster showed only snow.
A quick scan with a signal generator across the VHF channels proved to the technician that the varactor tuner actually was operating. However, it was tuned to frequencies without stations be cause the dc tuning voltages were all wrong. What caused the incorrect tuning voltages? The technician next picked up the probes of his dual-trace wide-band scope. By tracing the logic waveforms at test points in the digital control section, he soon uncovered the cause of the mistuning. One IC wasn't combining the pulses correctly. This changed the duty cycle of the output pulses. And, because the dc tuning voltages are determined by the duty cycle, the tuner was generating wrong frequencies.
Naturally, the technician needed to understand digitally-controlled tuners. But his ability to analyze digital pulses with his scope allowed him to find this defect without a lot of detours. He knew his wideband scope could display a faithful waveform of the pulses, so his analysis was not in doubt.
So ... what is wideband? Not very many years ago, a scope was considered to be "wideband" and good enough for TV work if it showed 3.58-MHz burst signals without serious attenuation. Such scopes were rated for bandwidths between 4 MHz and 5 MHz. Above those frequencies, the vertical amplifier response rolled off rapidly.
Today, most scopes have wider bandwidths and much flatter response curves. Many scopes in tended for TV servicing now offer response to 10 MHz or 15 MHz at +- 3 dB.
However, modern wideband scopes have response out to 25 MHz or higher. Improvements of stability from present-day solid state devices make possible high-gain, direct-coupled and wideband vertical amplifiers at moderate cost.
This is fortunate, for proper servicing of newer electronic products demands scopes with wider bandwidths.
Rise time--Ordinarily bandwidth is thought to refer only to frequency response. However, that is not the only reason for extending the bandwidth of scopes. Of equal value is an allied characteristic called "rise time." Rise time in scopes is a measure of how accurately the instrument reproduces pulses, especially the leading and trailing edges. (It is measured by the actual time required for the scope to trace between 10% and 90% of the pulse's total amplitude.)

-----Figure 1--This good waveform (produced by a 30-MHz scope) has vertical
leading and trailing edges (showing fast rise time), and sharp corners
without ringing. (B) The same pulses on a 15-MHz scope have tilted leading
and trailing edges (slower rise time), rounded corners with ringing,
and no leading edge on the first pulse (it has no delay line). Rise time
is related to bandwidth.
Wider bandwidth provides a shorter (faster) rise time. In turn, a shorter rise time allows the scope to produce a more faithful rendition of the actual pulse waveform.
The waveform photographs in Figure 1 illustrate the effects of two different rise times. Figure 1A shows the pulse rise time of a 30-MHz scope. Both the leading and trailing edges appear to be completely vertical and nearly invisible because the rise time is so short.
By comparison, the waveform of Figure 1B shows the same two pulses, but on another scope having a narrower (15 MHz) bandwidth and a longer (slower) rise time. The vertical lines are noticeably tilted and brighter than corresponding lines in the other picture. (This scope also has ringing at the pre-shoot and post-shoot corners from excessive compensation at too low a frequency.) Another important difference between the two scopes--but one that's not related to the rise time--is the missing leading edge of the left pulse in Figure 1B. It's caused by lack of a vertical delay line in that scope. More about this subject later.
These waveforms make clear that even moderate reduction of band width or a slower rise time can change the appearance of pulses enough to be significant.
Bandwidth vs. rise time--Rise time is a reciprocal (or inverse function) of bandwidth. Some examples will be given of this relationship.
A scope of 10-MHz bandwidth has a rise time of 35 ns. That sounds quite good. After all, it's just about one-third of a microsecond. But it's too slow for some kinds of present-day troubleshooting. Imagine trying to observe a waveform which has a rise time of only 10 or 20 ns. Such a waveform cannot be evaluated properly.
On the other hand, a bandwidth of 30 MHz provides a rise time of less than 12 ns. This minimizes errors when observing common digital pulses. However, to properly view pulses (such as glitches) in certain logic circuits, you might need an even wider bandwidth.
These are some of the reasons many TV manufacturers are recommending wideband scopes for servicing their receivers. Digital tuners, videocassette recorders, and IC count-down circuits have increased the demands on instruments and technicians alike.
One more comment about band width. The standard for bandwidth is a frequency response flat within 3 dB. That is, the rolloff or peaking of the response must not exceed 3 dB between the specified limits. However, not all manufacturers follow this way of stating band width. And specs can't be compared unless they observe the 3-dB standard.
Rise-time specifications all are rated by one standard, so far as I have found. So, rise time specs allow more accurate comparison of various scope models. As stated before, rise time is the time required for the scope to trace between the 10% and 90% voltage (amplitude) points of the waveform.
Incidentally, rise time can be converted to bandwidth in mega hertz by dividing the rise time (in nanoseconds) into 350.
Complex pulse waveforms--Merely owning a wideband triggered scope does not solve every servicing problem. It must be operated effectively and used constantly. Moreover, it is necessary to understand how to interpret what a quality scope can show. Beyond that, the operator should know ways of making the scope reveal everything about a waveform.
Think back to the transceiver problem and the special noise signal used by the communications technician. This noise signal comes from a Motorola model S-1359A generator, and it is a complex simulation of impulse noise found in automotive environments. If the noise signal is analyzed, a lot can be learned about how to produce helpful waveforms and how to interpret them with a wideband triggered scope.
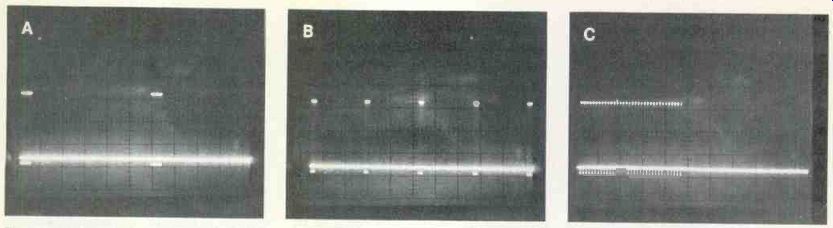
Figure 2--Using the simulated ignition-noise signal, this progression
shows how pulse details can be revealed by shorter sweep times. (A) The
pulses are stable, but appear blurred at 2 ms sweep. (B) A longer (slower)
sweep time shows more pulses. (C) A fast 0.2 ms sweep time reveals that
what appeared to be a blurred single pulse is a burst of very-narrow
pulses.
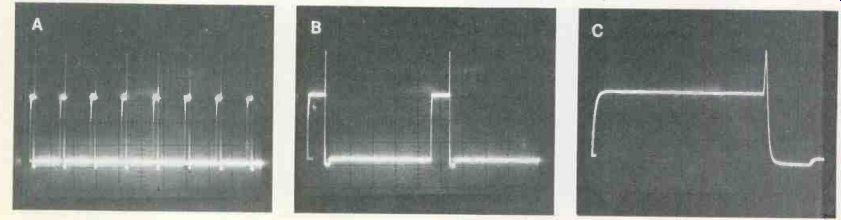
Figure 3 Additional expansion shows details of the burst pulses. (A)
Eight pulses are produced by a sweep of 20 us. The square tops and overshoots
are barely visible. (B) at 5 us, only two pulses are on the screen, and
details are more clear. (C) Sweep of 0.5 us allows a detailed inspection
of just one pulse.
Scoping the noise signal
According to a label on the noise generator, the repetition rate is 100 Hz. This means that one complete "cycle" of noise occurs 100 times per second. In other words, there are 100 noise pulses per second (PPS).
To properly display two pulse waveforms, select a total horizontal sweep time equal to the time of two "cycles." On a calculator, take the reciprocal of the repetition rate.
This gives the time of one pulse.
Then double it for two. That's the time for sweeping the entire screen.
However, the screen has 10 divisions, so divide by 10 to obtain the time in seconds per division. These are the three calculations:
1=100= .01
.01 X 2 = .02
.02 x 10 = .002 seconds
Adjust the scope for 2 ms/div.
However, understanding how the time is calculated, there is a shortcut. To obtain the time in seconds, divide 0.2 by the repetition rate in Hertz.
Of course, the waveform must be locked solidly. The method isn't given here, because it varies with the brand and model.
Figure 2A shows two pulses from the S-1359A. Slowing the sweep to about double time increases the number of pulses (Figure 2B).
Neither sweep time reveals any detail of individual pulses. However, they are useful for measuring the repetition rate. (Reciprocal of the time of one "cycle" is the repetition rate.) To expand one pulse and show the details, it is necessary only to shorten the sweep time. Figure 2C shows how a 0.2 ms sweep expands one pulse to fill almost half of the scope screen. Surprise! Previous waveforms indicated each pulse was solid, but actually each is made up of many narrow pulses. It is a burst of pulses.
This faster horizontal-sweep time enables measuring the burst duration. Full width of the screen is 2 ms, and the burst occupies about 4.6 divisions or 46% of the width.
In round numbers, the burst width is slightly less than 1 ms. Although no details of the pulses in the burst can be seen, it is possible to count 35 of them.
So far, the pulse-waveform analysis (made possible by a wideband triggered scope) has determined these characteristics:
the repetition rate in pulses –per-second, or the frequency in Hertz;
repetition time in seconds, milli seconds, or microseconds (this is the inverse of repetition rate);
pulse width (or duration), which sometimes is called period.
It is the "on" time of each pulse; and the actual waveshape, including any overshoot, undershoot, rounding, ringing, slow rise time and other characteristics of a waveform.
There's more
Even more expansion can be made with the scope. Figure 3 illustrates three steps of expansion, showing 8 pulses, 2 pulses, and finally just one pulse.
Waveform magnification of this kind is possible only by use of a triggered scope. Any practical sweep time can be selected, the starting point is the same for each waveform, and it's not necessary to lock the sweep for each new time.
At best, a recurrent-sweep scope could show blurred "pulses" when synchronized to the basic 100-Hz repetition rate.
In Figure 3A, the time-base switch is set for 20 us .per division.
Eight of the narrow pulses can be seen clearly. In fact, they are square-topped pulses, and each one has a narrow positive pulse at the falling side. The rep rate of these burst pulses can be measured approximately. Each requires about 28 us, so divide 0.000028 into 1 to obtain the rep rate of 35,714 Hz. However, the duration (pulse width) can't be calculated yet. For that, the display must be spread even more.
Move the time-base switch to 5 us/div (Figure 3B). Now with two pulses on the screen, the rep rate is found to be 27.5 ms or about 36.5 kHz. Notice the increased accuracy.
Also, the waveform can be studied in finer detail, especially the fast preshoot at the top and the small overshoot at the bottom of each trailing edge.
Maximum accuracy and visibility of the entire pulse are obtained by changing to a sweep time of 0.5-us/div. This shorter time shows the single-pulse duration to be 7.8 divisions. Multiplied by 0.5 us, this is 3.9 us. That's a very fast pulse! If it were allowed to run constantly (instead of in a burst), the rep rate would be about 246-kHz. Also, these sharp rise and fall times generate many higher harmonics far into the megahertz region.
Duration of the overshoot at the bottom of the trailing edge (Figure 3C) can be measured by the 1.8 divisions it occupies. This calculates to about 0.9 us. But its amplitude is comparatively minor, so this overshoot has little influence on the overall content of the signal.
Why signal delay? In Figure 3C, look carefully at the positive pulse that is above the main pulse trailing edge. It can be seen clearly, but the width is too narrow for any measurement. If you try to spread it out by switching to a 0.1 us time base, there is a bad problem. The triggering point remains at the upslope of the leading edge, and the whole 10 divisions of graticule represent 1 us. However, the entire pulse has a duration of 3.9 us, which drives the trailing edge and the preshoot pulse far off of the screen to the right. The pulse now can't be seen or measured.
Of course, the triggering point can be changed, which is easy to do. Just shift the triggering level to a higher point, above the flat top of the main pulse. The display now starts at the preshoot pulse and it can be widened as much as desired.
Unfortunately, if this is at tempted on an ordinary triggered scope, there will be another insurmountable problem (Figure 4A).
Although the scope is set to trigger on the positive upslope of the preshoot, the display on the screen begins on the downslope. The left part of the pulse is missing, so the pulse can't be measured.
This illustrates another advantage of scopes that have signal delay.
Anytime it is necessary to view complex waveforms or pulses that have durations shorter than about 0.05 us, a delay line is needed in the vertical-signal amplifiers.
Otherwise, the signal has gone through part of its own cycle or duration before the triggering system can get the horizontal sweep to moving. In many published wave forms this is represented as a missing leading edge of the first pulse (also, see Figure 1B).
The solution is a vertical-signal delay line that slows down the signal, giving the sweep time to start.
Don't confuse this signal delay with trigger delay, which is an entirely different feature found in more elaborate scopes. Signal delay often is included in scopes that have bandwidths above 20 MHz.
Scopes of less bandwidth can't cope with extremely short pulses, any way.
Figure 4B shows the preshoot pulse on a wider-bandwidth scope having a signal delay of about 50 ns (0.05 us). Now the entire preshoot pulse is visible. Also, it can be measured. Rotate the vertical-position control to place the 20% points on the x-axis line of the graticule and the leading edge exactly at the left edge. The pulse duration is about 0.05 us or 50 ms, which represents a signal of 10 MHz, if it were repetitive. That's why this test signal can simulate auto ignition so successfully.

Figure 4--For examination of the trailing edges, triggering can b obtained
from the positive preshoot that is there. (A) An ordinary scope without
signal delay shows only part of the preshoot. (B) Wideband scope with
signal delay shows all of the narrow preshoot so it can be measured.

Fig. 5--magnifier often permits expansion without changing trigger points,
and gives better accuracy. (A) This is the pulse with the positive pre-shoot
that's to be examined. (S) A faster sweep moves the preshoot off the
screen, but rotating the Hickok multiturn positioning control moves the
magnified preshoot back to the screen. (C) The expanded pulse has been
positioned for measurement of the duration.
Helpful alternative
Many triggered scopes have a 5X "expander" which can be switched on to increase the sweep width by a factor of five. The waveform is expanded, of course, but only a fifth is visible at any one time. To find any certain part of the expanded waveform, the horizontal-positioning control must be rotated until the desired section can be seen on the screen. Unfortunately, any locking jitter is magnified five times also. In addition, the wave form brightness is reduced severely.
That's because the trace is missing from the screen for four-fifths of the time.
A unique feature of the Hickok model 532 (a 30-MHz scope chosen for this demonstration) is the full-time 4X expander. It's not necessary to switch it in, because it operates all of the time.
To demonstrate this operation, a progression from the waveform of Figure 3C to the Figure 4B wave form will be discussed.
Easy expansion--Figure 5A shows the complete pulse obtained at a sweep time of 0.5 us. Previously, when the sweep was set to 0.1 us in a futile attempt to magnify the trailing-edge preshoot, the preshoot was forced off of the right edge of the screen where it could not be seen or measured. This time the sweep time again is set to 0.1 us, but the triggering won't have to be juggled to see the trailing preshoot.
Just rotate the horizontal-positioning control, moving the waveform to the left (see Figure 5B) and stop when the trailing preshoot is positioned as shown in Figure SC.
In this example, the final result was the same as that of the other method. However, not all wave forms will have a convenient positive pulse that can be used for auxiliary locking. One value of the constant 4X feature is that it allows expansion regardless of the wave-shape.
No calculations are required to use the 4X feature. The sweep time is not changed, and the brightness of the trace is not decreased. These add to valid advantages.
Comments As you can see from these examples, a wideband triggered scope is not just an ordinary triggered scope that is beefed up.
The differences are important.
Two of these advantages are shown in the waveforms of Figure 1. The scope of Figure 1B was a 15-MHz triggered model, but with out a delay line. Therefore, the corners were rounded, some ringing was visible, and the rising and falling lines were tilted (indicating a slow rise time). Contrast those characteristics with the excellent pulses of Figure 1A which were produced by the Hickok 30-MHz scope.
Notice, too, that the wideband waveform showed the rising edge of the first pulse (because it has a signal-delay line) while that edge was missing in the other waveform.
These advanced features justify the price of a truly wideband scope right now. They will be indispensible in the near future.
Also see: Tips for using scopes--part 1