By Jack Webster
Subtraction, multiplication and division are performed by addition in the microprocessor arithmetic-logic unit (ALU). In previous articles, microprocessor terminology was discussed along with descriptions of each basic section and function. Although this article is the last of the series, additional information will be presented at irregular intervals.
Binary addition
A previous discussion of binary arithmetic is continued here. As stated last month, there are only four possible additions for binary numbers (highs and lows, or ones and zeros). These are the four forms:
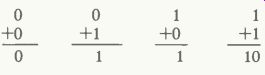
Larger numbers are added by combining these four forms.
In the case of 1+1, a zero is marked on the paper and the 1 is carried to the next step. as shown in these examples:
Decimal addition

above: Shown approximately life-size is an 8080 N-channel 40-pin 8-bit microprocessor. The chip inside is even smaller.
Binary addition

The second binary addition has 1+1 = 10 in the right-hand column. The zero is marked down and the one is carried for addition to the two ones already in the next column. They are added as 1+1 = 10 and 10+1 = 11, so the one is marked down and the other one is carried. Again, the same addition happens in the left-hand column.
This can be illustrated by the following:

Binary 11000 equals decimal 16 + 8+0+0+0= 24.
Binary subtraction
One way to accomplish binary subtraction is to start with the same four examples of addition but modified as shown:

* Note: borrow a 1 from the next column to the left.
When the subtrahend is larger than the minuend, it is necessary to borrow a 1 from the previous column. This is similar to the traditional method of subtracting decimal numbers, as shown in the next example.
26 (minuend)
-19 (subtrahend)
-----
7
The 9 in the right-hand column is larger than the 6 in the minuend, so it cannot be subtracted in the usual way. Instead, a 1 is borrowed from the next column, and the problem has the following inter mediate form:

The same procedure can be used for binary numbers also, as shown by a simple example.

After borrowing 1 from the second column, the subtraction problem appears this way:
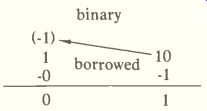
The answer can be checked by adding the difference to the subtrahend which produces the original minuend. For example in this problem, the difference (1) plus the subtrahend (1) equals the 10 minuend. Or, 1 + 1 = 10 in binary.
Complements
In the September microprocessor article were examples of subtracting decimal numbers by adding certain numbers and their mathematical complements.
Similar computations can be done with digital numbers, but first a definition of digital complements must be presented. The one's complement of a binary number is obtained by changing all zeros to ones and also changing all ones to zeros, as shown in this example:
binary number: 0 1 1 0 1 0 1 1
one's complement: 1 0 0 1 0 1 0 0
Incidentally, the one's complement at one time was used to represent negative numbers. The left-hand digit in an 8-bit word was used to represent the positive or negative sign of that number.
For example, the number +7 was represented by 0 0000111. The one's complement (1 1111000) of that number represents-7. The left-hand digit is called the most significant bit (MSB), and the number is positive when the bit is 0 and it is negative when this bit is 1.
The two's complement of a number is found by taking the one's complement and adding a binary 1. In the previous example, the 8-bit word for number 7 is 00000111. This is the sequence for obtaining the one's and two's complements:
7 decimal is 0 0000111 one's complement is 1 1111000
add binary 1 +1
two's complement 1 1111001
Subtraction with two's complement
Microprocessors do not have any circuitry for subtracting numbers directly. Instead, the subtracting is performed by adding the two's complement of the subtrahend.
For example, 11 is subtracted from 19 first in the usual binary fashion, followed by subtraction by two's complement, as shown here:

Note: discard last carry
Microprocessor circuitry can be simplified greatly by performing subtraction with binary addition as illustrated. Actually, the two's complement of a number is the microprocessor's method of writing negative numbers. In other words, 00001011 is the 8-digit word for decimal +11, and the 11110101 two's complement is the 8-digit word for-11. Adding a-11 is the same as subtracting a +11.
Multiplication and division
Division and multiplication also can be performed by addition. For example, both conventional and multiplication-by-addition are illustrated next for the problem of multiplying 17 by 7.

Essentially the same procedure can be used with binary numbers.
Division also can be accomplished by subtraction as shown in the following example where 64 is divided by 16.

After 16 is subtracted from 64 four times, the remainder is 0; therefore, 64 divided by 16 equals 4.
Microprocessors do not subtract numbers. Instead, they add the two's complements. If this problem had been solved with binary rather than decimal numbers, the two's complement of 16 could be added for 4 times to obtain a 00000000 reading.
Performing subtraction, division and multiplication by addition would be very inefficient if done by a human. But digital circuits calculate so rapidly that the extra time required by using addition for everything is of little consequence.
This concession allows the design of ALUs to be less complicated.
Summary
Various articles in this series have explained that a typical micro processor IC has an arithmetic-logic unit (ALU) for computations, a section of read-only memory (ROM) for permanently stored date, some random-access memory (RAM) that can receive and store data which later can be used or replaced with new, usually a clock (oscillator) for synchronizing the operations, and also input and output ports.
All inputs to a microprocessor must be either high (near supply voltage) or low (almost ground potential). These input signals can be dc digital pulses or dc steady voltages made high or low by external switches. No varying or intermediate-voltage signals should ever be applied.
Likewise, all outputs from each microprocessor are highs or lows that can be either patterns of do digital pulses or steady high and low dc voltages. These outputs can activate external circuitry that operates LEDs, relays or other peripheral equipment.
If a microprocessor is called on to accept an input from an analog (varying-amplitude) signal, an analog-to-digital converter must be used as an interface. Similarly, a digital-to-analog converter can be employed at some output ports to recover the analog equivalent of a digital signal from the microprocessor.
A microprocessor system that might include additional memory and support ICs on a module or circuit board plus any related input and output equipment is called "hardware." Manuals and programming sequences for microprocessor or computer operation are known as "software." The cost of developing the soft ware and debugging it is far more expensive, in many cases, than the price of the microprocessor equipment alone. This unique unbalance of costs occurs because microprocessors are general-purpose devices.
They are extremely versatile, but do not accomplish anything without outside help.
Therefore, many of the tasks assigned to microprocessors utilize only a small percentage of their total resources. This probably is true of the microprocessors used in TVs and other home-entertainment equipment; and it is fortunate, otherwise the servicing would be nearly impossible.
Look at one example. Suppose a certain microprocessor had a 1056-bit ROM that needed testing.
Imagine manually switching 8-bit signals as inputs and monitoring the correct outputs for 1056 separate tests! Of course, testing the ALU and RAM sections would require similar excessive times. IC manufacturers have special test equipment that makes all checks automatically. Such equipment is too expensive for troubleshooting in the field.

---------- For the Motorola model MCM1452 1024-bit Read-Only Memory
(ROM), one picture shows the entire IC chip, which is about a quarter-inch
square. The other is a 27-times enlargement of one corner of the same
chip. (Courtesy of Motorola)
Microprocessors in TVs
Practical in-circuit tests of micro processors used in the tuner-control sections of newer color TVs are not as difficult as previously stated.
Probably most functions will operate normally, thus allowing more time for the few items remaining.
Generally, the techniques will be similar to those used now with other ICs. Make certain the supply voltage (or voltages) is correct and without excessive hash. Check for the proper input digital signals.
And finally, verify the absence of the normal output highs and lows.
If no wrong conditions are found (except the lack of output), then" replace the IC.
After more of these microprocessor-controlled color receivers are in the field, Electronic Servicing will supply its readers with trouble shooting procedures for specific models.
Also see:
Calculators make milli micro decimals easy