A series of projects for the not-so-experienced constructor. Although each article will describe in detail the operation, use, construction and, where relevant, the underlying theory of the project, constructors will, none the less, require an elementary knowledge of electronic engineering. Each project in the series will be based on inexpensive and commonly available parts.

PHASE METER
Phase, phase difference and phase shift are commonly used terms in electronics theory. Where an oscilloscope or a vectorscope are not available, a special test instrument is required to measure phase shift so that it can be checked against the calculated value. Such an instrument is described here.
by J. Bareford
THE term phase is used when describing two or more alternating voltages of which the frequency is equal, while their zero-crossings occur at different instants. An alternating voltage crosses the zero line when its instantaneous voltage is nought. An example of two alternating voltages of different phase is shown in the oscilloscope photo graph in Fig. 1. The phase difference is about one sixth of the period in this case. The difference is, however, more commonly ex pressed as an angle because a sine-wave is periodical, so that its period, T, may be de scribed as a circle, or 360°. This means that any part of the period may be expressed in degrees: a period of 0.25T, for instance, equals 90°, 0.10T equals 36°, etc. The phase shift between the two sine-waves in Fig. 1 is, therefore, roughly 60°. What causes phase shift? Since the phase difference between two separate voltage sources is hardly ever constant because of small frequency deviations, it makes little sense to design a test instrument for this purpose. The meter described here, however, is intended to locate signal changes that occur in a circuit. Take, for instance, an inverting amplifier. The term 'inverting' implies that the input and output signals are 180° out of phase. In some cases, it is useful to be able to check this.
Transistors and opamps are not the only components that can cause phase shift. Capacitors and inductors introduce a phase shift of 90° between voltage and current. In the case of the capacitor, the voltage lags the current by 90° (see Fig. 2). Inductors have the opposite behavior: the current lags the voltage by 90°.
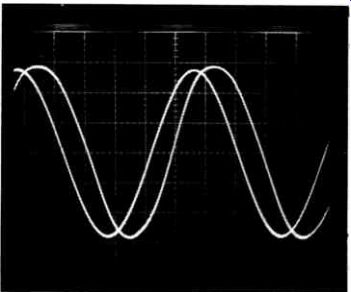
Fig. 1. Two sine-waves with a phase shift of about one sixth of the period,
or about 60 degrees.
Capacitors and inductors are typically used in filters. An example is shown in Fig. 3.
In this circuit, one would expect the output voltage to be in phase with the current through the capacitor, i.e., there exists a phase shift of 90° between the input and the output. Unfortunately, this is not so because the phase shift depends on the frequency (the actual relation is an inverse one). The de pendency is caused by the ratio of the capacitor's reactance to the resistor value. Since the reactance, x c , is inversely related to the frequency, it is large with respect to the (fixed) resistor value at low frequencies. Hence, the phase difference is roughly 90° at low frequencies, and 0° at high frequencies.
Phase difference: what it does
In many case, the phase relation between alternating voltages is of little or no importance. There are, however, situations in which the phase relation is all-important. Take the case of two alternating voltages that are to be added. If they are 180° out of phase, the summing operation would result in total cancellation of the two, i.e., an output of 0 V. The equalizing current that flows as a result of this operation is wasted.
In large power plants, phase differences and the resulting equalizing currents must be kept to a minimum. Generators are, there fore, electrically coupled to maintain synchronicity. Furthermore, many power plants are linked by a special network, which often extends beyond country borders.
Fortunately, problems with phase differences in power plants need not bother us here, and can be safely left to power electricity engineers. The stereo equipment in your living room may, therefore, be a better example to illustrate the importance of steady phase relations. Since any amplifier in the system is bound to contain a filter of some kind, it may be expected that there is some phase shift between the input source, e.g., a CD player, and the output, the loud speaker. Evidently, it is desirable for this shift to be roughly the same over the full frequency range of the signal. If this is not so, the sound is not perfect, particularly when the phase differences between the left and the right channel is large.
A final example of a circuit in which phase shift is all-important is the oscillator, which functions only when the amplified output signal is fed back to the input at a phase shift of 0°.
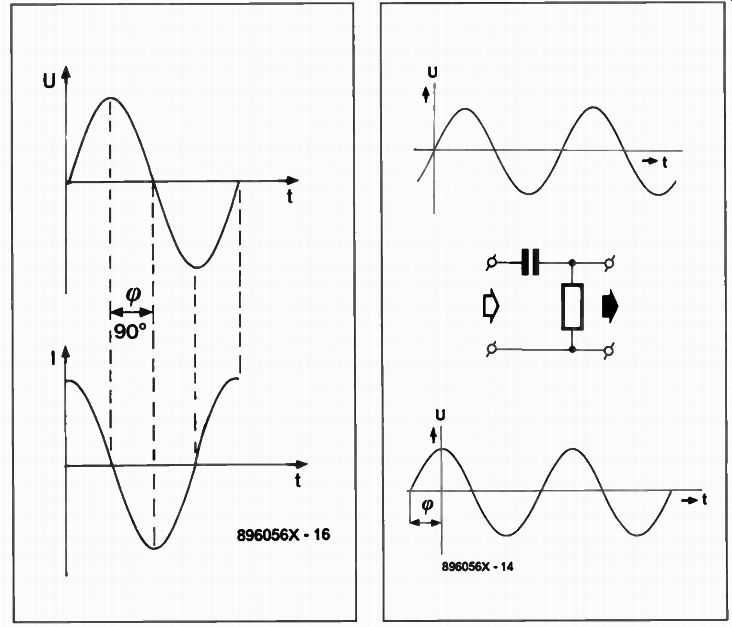
Fig. 2. The voltage on a capacitor
lags the current by 90 degrees.
Fig. 3. Phase shift introduced by an R-C network
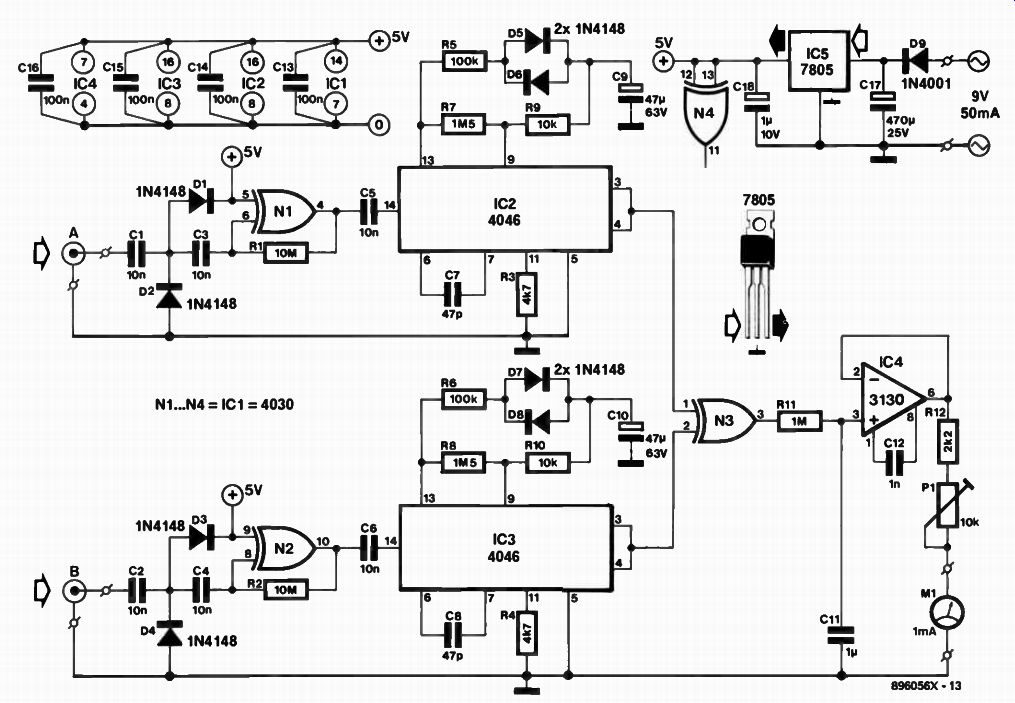
Fig. 4. Circuit diagram of the phase meter. The crucial part is XOR gate
N3 which produces a voltage as a function of the phase difference that exists
between the signals applied to the A and B inputs of the meter.

Fig. 5. Track layout and component mounting plan of the PCB for the phase
meter.

Components List:

----------
The phase meter
As illustrated in Fig. 1, a two-channel oscilloscope is perfect for measuring phase differences. Unfortunately, such an instrument is not available to every one, and this is where a special phase meter comes in.
The circuit diagram of the two-channel phase meter is shown in Fig. 4. The capacitors at inputs A and B block any d.c. components in the signals applied to the circuit.
Diodes D1 - D4 protect amplifiers N1 and N2 against negative or too high voltages. The amplified signals are subsequently fed to IC2 and IC3, two phase-locked loops (PLLs) that track the input frequencies and convert them to digital signals with a fixed duty factor of 0.5 and a swing of 5 Vpp. The low-pass filters of these PLLs are special types to enable the 4046s to keep track of fast frequency changes in the input signals. This important characteristic is provided primarily by the diodes in the network connected to pins 13 and 9.
The actual phase comparator is formed by a single XOR (exclusive-OR) gate, N3. The output signal of the gate is averaged by integrator network
The larger the phase difference between the two input signals, the larger the voltage supplied by buffer IC4.
Moving-coil meter M1, resistor R12 and preset P1 together form a meter that indicates the phase shift. Since the voltage indicated by the meter lies between 0 V and the positive supply level, the circuit must be powered from a regulated supply. A three terminal fixed voltage regulator Type 7805 is used here for this purpose. The minimum unregulated or alternating input voltage is 9 V. Construction and setting up
The circuit is best constructed on the printed circuit board shown in Fig. 5. First, fit the two wire links so that they are not forgotten later.
Pay attention to the orientation of the polarized components (diodes, transistors, ICs and electrolytic capacitors). Fit IC sockets for all ICs.
To align the meter, first remove IC2 and IC3 from their sockets. Connect pin 3 of the socket for IC2 to pin 5 (ground) via a 10 k-O resistor. Next, connect pin 3 of the socket for IC3 to pin 16 (+5 V) via a 10 k-O resistor.
Switch on and check that pin 1 of N3 is at about 0 V, and pin 2 at about +5 V. The out put of the XOR gate, pin 3, should be at +5 V. Since this represents the maximum phase shift that can be measured between the two channels, adjust preset P1 until a meter indication of 180° is obtained.
Remove the two 10-k-Ohm resistors and fit the two 4046s. At this stage, the circuit is ready for fitting into an enclosure.
Although the indication range of the meter is, in principle, limited to 180°, it is possible to measure greater phase shifts. A shift of 270°, for instance, is indicated as 90° because the meter can not detect which channel, A or B, was high first.
Also see: Electronics Scene: Four-Channel Digital Delay / Pulse Generator