This Section offers an introduction to the subject of frequency and a spot review of those alternating-current fundamentals needed by anyone dealing with frequency. The known range of frequencies generated by man and by nature is wide indeed. Some notion of this tremendous scope can be gained from this Section, even if our immediate concern in electronics is with the frequency of alternating electric currents and voltages.
For a broader view of related theory, the reader may consult the Sections on alternating currents and on electromagnetic radiation in standard textbooks of electrical engineering and physics.
1.1 BASIC DEFINITION
The term frequency (symbol, f) has different meanings in different fields. In the electrical sciences, however, this term denotes the number of times in one second that an alternating current or voltage repeats a complete cycle. [1] A complete cycle is usually understood to be the single, uninterrupted sequence of changes that a current or voltage goes through as it starts from zero, reaches a maximum positive value, returns to zero, reaches a maximum negative value, and finally returns to zero.
[1. Frequency is used sometimes to mean the number of electrical pulses per second, but the specific term pulse-repetition rate (abbreviated prr) or pulse-repetition frequency (abbreviated prf) usually is preferred.]
(A) Sine wave. (B) Square wave. (C) Triangular wave.
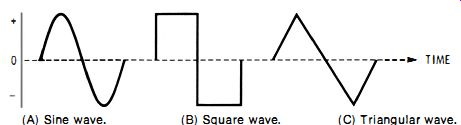
Fig. 1-1. Typical single ac cycles.
Such a single, complete cycle is illustrated by Fig. 1-1 (Fig. 1-1A for a sine wave, Fig. 1-1B for a square wave, and Fig. 1-1C for a triangular wave). The cycle may have any waveform whatever and may be symmetrical or asymmetrical.
Unlike the situation in Fig. 1-1, a cycle may also have its negative peak first and its positive peak last.
Often, a cycle does not begin and end at zero at all, but at some definite value of current or voltage, as shown in Fig. 1-2.
In Fig. 1-2A, the cycle swings between +1 and +3 (volts or amperes ), with +2 as the mean value or reference level ; in Fig. 1-2B, it swings between -1 and -3 (volts or amperes ), with -2 as the mean value. Such a quantity is properly called an alternating component or ac component. It is also called a fluctuating voltage or current, composite voltage or current, or ac superimposed on dc. While a sine wave is shown in Fig. 1-2, the cycle may have any other waveshape, as well. It should be noted, however, that whether the cycle alternates about zero (Fig. 1-1 ) or about some finite current or voltage (Fig. 1-2), its identity as the basic component of frequency remains the same. It should be noted also that the cycle may not necessarily have the smooth shape shown in Figs. 1-1 and 1-2, but may be distorted. Even when distorted, it is still a cycle, although the distortion may adversely affect the operation of some electronic instruments.
(A) Positive fluctuating. (B) Negative fluctuating.

Fig. 1-2. Typical single fluctuating cycles.

Table 1-1. Values of Frequency Units
1.2 UNITS OF FREQUENCY
The basic unit of frequency is the hertz (abbreviated Hz), named in honor of Heinrich Hertz (1857-1894) who first demonstrated radio waves. The hertz is equal to 1 cycle per second : 1 Hz = 1 cps (Eq 1-1 )
Because the hertz is such a small unit for designating high frequencies, larger multiples are used much of the time. These are kilohertz, kHz (one thousand hertz ) ; megahertz, MHz (one million hertz ) ; gigahertz, G H z (one billion hertz ) ; and occasionally terahertz, THz (one trillion hertz ). Table 1-1 shows the various units of frequency and the corresponding number of cycles per second.
Table 1-2 gives multipliers for easily converting frequency units in Column 1 to frequency units in the other columns.
Example: To convert frequency in MHz (Row 3) to frequency in GHz (Column 4) , multiply MHz by 0.001. Similarly, to convert to kHz to Hz, multiply kHz by 1000. Illustrative example: The video carrier of tv Channel 13 has a frequency of 211.25 MHz. What is this frequency (fo) in kilohertz? From Table 1-2, the multiplier for MHz to kHz is 1000. Therefore, fo = 211.25 X 1000 = 211,250 kHz.

Table 1-2. Multipliers for Converting Frequency Units
1.3 FREQUENCY DOMAIN
Encounterable frequencies cover the vast range between 0.00005 Hz (produced by a laboratory-type function generator ) to more than 30 million THz (the frequency of some gamma rays). In between lie frequencies in the following categories which include the alternating and oscillating phenomena with which science presently is concerned. [[ Authorities disagree as to the limits of these categories. The figures given here represent a reasonable consensus. ]]
1. Subaudible frequencies-Frequencies lower than 20 Hz.
They are so called because their effects are below the usual range of human hearing. These frequencies are also termed subsonic.
2. Audio frequencies (abbreviated af )--20 Hz to 10 kHz.
This band of frequencies is so called because their effects are audible to the usual human listener. Frequencies higher than 10 kHz accordingly are sometimes called super-audible or supersonic, and often ultrasonic frequencies.
3. Radio frequencies (abbreviated rf)--10 kHz to 30,000 MHz. This band comprises the frequencies that make possible radio and the associated processes of television, radar, and remote control. The Federal Communications Commission has subdivided the rf spectrum into the following sections : Very-low frequencies (vlf) --10 to 30 kHz.
Low frequencies (lf)--30 to 300 kHz.
Medium frequencies (mf)--300 to 3000 kHz.
High frequencies (hf)-·
Very-high frequencies (vhf)-30 to 300 MHz.
Ultrahigh frequencies (uhf)--300 to 3000 MHz.
Super-high frequencies (shf)--3000 to 30,000 MHz.
Radio frequencies of 1000 MHz (1 GHz ) and higher are usually termed microwave frequencies. Electronics people have coined several terms to designate special functions, but these latter are not standard categories.
One of these is the term intermediate frequency (abbreviated i-f). A usable intermediate frequency might conceivably come from any part of the wide radio-frequency spectrum. For example, the intermediate frequency used in an a-m broadcast receiver is in the medium-frequency range (455 kHz), the one used in the sound channel of a tv receiver (4.5 MHz) or in an fm receiver (10.7 MHz) is in the high-frequency range, and the one used in the first i-f stage of a tv receiver (44 MHz) is in the very-high frequency range.
4. Light-300 GHz to 300,000 THz. The light spectrum lies just above the radio-frequency spectrum and is subdivided as follows : Infrared rays (ir)-300 to 428,570 GHz.
Visible light-428,570 to 750,000 GHz.
Ultraviolet rays (uv)-750,000 GHz to 300,000 THz.
5. X-rays-300,000 to 30,000,000 THz. X-rays have considerable use in industry, medicine, and science research. They are usually generated by X-ray tubes, but they also arise secondarily from the operation of certain high-voltage electronic equipment, such as some tv receivers, and have been detected in the sun's radiation. Some authorities show an overlap of X-rays and high-frequency ultraviolet rays.
6. Gamma rays-3,000,000 THz and above. Note that here there is overlap down into the X-ray range (some authorities assert that gamma rays are the same as X-rays, but mostly of higher frequency). Gamma rays are a byproduct of radioactivity-man-made, as well as natural. Beyond gamma rays lie cosmic rays, but these latter are regarded by some scholars as fast-moving subatomic particles and not rays at all in the sense of oscillating energy.
In conventional electronics, frequency measurements are restricted to a portion of this wide electromagnetic spectrum, the part extending from subaudible frequencies through in-use microwave radio frequencies (roughly 0 to 40 GHz). This means that our first concern is with the frequency of alternating electric currents and voltages and of the fields they set up, and only occasionally with other electromagnetic phenomena, such as light, X-rays, and gamma rays.
1.4 FREQUENCY VS WAVELENGTH
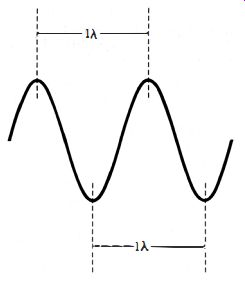
Fig. 1-3. Significance of wavelength.
When dealing with electromagnetic waves, it is often preferable to use the wavelength (A) rather than the frequency of a radiation. Wavelength is the distance measured from crest to crest or from trough to trough over two consecutive cycles of the radiation (see Fig. 1-3). The higher the frequency, the shorter the wavelength, and vice versa. Wavelength is expressed in meters ( m), centimeters ( em), or millimeters (mm), and may be determined from the frequency in the following manner : where,
A - 300,000,000
f (Eq 1-2)
300,000,000 (meters per second) is the speed of light,
A is the wavelength in meters,
f is the frequency in hertz.
Thus, the wavelength of a 100-kHz signal equals 300,000,000 -= 100,000 = 3000 m. In some situations, wavelength is more easily measured than frequency ; and in such a case, frequency would be calculated from the measured wavelength (see Equation 1-4). Like frequency, wavelength covers a wide territory. At one extreme, A for certain X-days may be only 1/100,000 of a millimeter ; and at the other extreme (low audio frequencies), the wavelength of 60-Hz power is 5,000,000 meters (3105 miles). Obviously, if frequency is expressed in units other than hertz, the numerator 300,000,000 must be changed accordingly.
General formulas for this purpose are given in Equations 1-3 and 1-4 :
where,
A is the wavelength, f is the frequency, A = vlf v is the velocity of light, or a suitable sub-multiple.
(Eq 1-3)
f =v/'A (Eq 1-4)
where, f is the frequency, v is the velocity of light, or a suitable sub-multiple,
'A is the wavelength.
The values of v to be used with selected units of frequency are given in Table 1-3. Thus, for wavelengths in meters and for frequency in kilohertz, v = 300,000 ; for wavelength in centimeters and for frequency in gigahertz, v = 30 ; and so on.
Illustrative example: What is the wavelength in meters corresponding to the Citizens band frequency of 27.025 MHz (Channel 6)? From Table 1-3, for the MHz-to-m conversion, v = 300. Therefore, from Equation 1-3, ). = 300/27.025 = 11.1 m.
Illustrative example: What is the frequency in kilohertz corresponding to the 75-meter amateur wavelength? From Table 1-3, for the m-to-kHz conversion, v = 300,000. Therefore, from Equation 1-4, f = 300,000/75 = 4000 kHz.
A complete list of formulas for frequency-to-wavelength and wavelength-to-frequency conversions is given in Appendix B. Multiplier-type conversion factors for changing wavelength and frequency units of one magnitude to those of another magnitude are given in Appendix A.
Table 1-3. Value of Numerator (v) in Equations 1-3 and 1-4

Table 1-4. Value of Numerator (x) in Equations 1-5 and 1-6
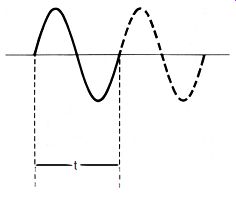
Fig. 1-4. Significance of period.
1.5 PERIOD
At any frequency, the time interval between the beginning and end of one cycle is termed the period (symbol, t) ; see Fig. 1-4. The higher the frequency (shorter the wavelength ), the r r shorter the period, and vice versa. Period is expressed in seconds (s), milliseconds ( ms ), or microseconds (uS), and may be determined from frequency in the following manner ; t_seconds = l/f_hertz. Thus, the period of the 60-Hz power-line voltage is 1/60 = 0.0167 s. Obviously, if frequency is expressed in units other than hertz, the numerator must be changed accordingly. General formulas for this purpose are : t = x/f where, t is the time, x is the special numerator (see Table 1-4), f is the frequency.
f= x/t where, f is the frequency, x is the special numerator (see Table 1-4), t is the time.
(Eq 1-5 )
(Eq 1-6 )
The values of x to be used with selected units of frequency are given in Table 1-4. Thus, for frequency in kilohertz and for period in microseconds, x = 1000; for frequency in hertz and for period in milliseconds, x = 1000; and so on.
Illustrative .example: What is the period in milliseconds of a 400-Hz current?
From Table 1-4, for the Hz-to-ms calculation, x = 1000. Therefore, from Equation 1-5, t = 1000/400 = 2.5 ms.
Illustrative example: What is the frequency in megahertz corresponding to a period of 5 us? From Table 1-4, for the us-to-MHz calculation, x = 1. Therefore, from Equation 1-6, f = 1/5 = 0.2 MHz.
A complete list of formulas for frequency-to-period and period-to-frequency conversions is given in Appendix C.
(A) In phase. (B) Out of phase.
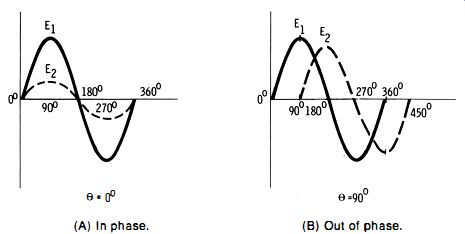
Fig. 1-5. Simple phase relationships.
1.6 PHASE
Phase relations sometimes must be taken into consideration in frequency measurements. Two or more varying phenomena (e.g., currents, voltages, waves ) are said to be in phase when they reach each of their corresponding values at the same instant and in the same direction; they are said to be out of phase (by so many electrical degrees--the angle theta) when they are not so in step with each other. The separate phenomena need not have the same amplitude.
Fig. 1-5A shows two ac voltages which are in phase (theta = 0°) ; Fig. 1-5B shows two ac voltages which are everywhere 90° out of phase with each other (theta = 90° = pi/2 radians). These components have the same frequency, but E2 is lower in amplitude than E1 in this instance. When components differ in frequency, they will be in phase at some points and out of phase at others (when currents are in phase, they add; when they are out of phase, they subtract). Two equal-amplitude components that are of the same frequency but are 180° out of phase at all points completely cancel each other.
In a purely resistive circuit, current and voltage are in phase. In a purely capacitive circuit, current leads voltage by 90°. In a purely inductive circuit, current lags voltage by 90°. In an RC, RL, LC, or LCR circuit, the phase angle and whether the current leads or lags are determined by the magnitudes of resistance and reactance present; whether the latter is capacitive, inductive, or both; and whether the components are in series, parallel, or some combination of the two.