
Fig. 201. Ideal equalizer characteristic.
EQUALIZER circuits look deceptively simple: a few resistors and a capacitor or two; but even when prescribed values are used they may fail to deliver the expected results. Many articles and books on the subject safeguard themselves against this possibility with a post script to the effect that "The foregoing method will provide rough values. Exact values for any specific application will have to be deter mined by test." In other words, "This gives you a general idea; if you eventually get it right. If you haven't -well, just hope for the best." Fortunately, this rather pessimistic approach to equalizer design is quite unnecessary if you understand and use the right methods. An equalizer has to provide a definite boost (or drop) in the response of a circuit between two specified frequencies. The amount of boost or drop may be expressed in decibels, or as a voltage ratio (db units are generally used in audio work). Since the two limit frequencies--called "turnover points"--are usually fairly far apart (at least in standard recording practice) an ideal equalizer would have the characteristics shown in Fig. 201. The response of the circuit (E1 ) is perfectly flat up to the lower turnover point (F1); then it drops uniformly to the desired level (E2) at the high-end turnover frequency (F0); then flat tens out again.
Fig. 202 shows two basic resistance-capacitance equalizer circuits.
The arrangement in Fig. 202-a is for high-frequency boost; Fig. 202-b is for low frequency boost. (Inductors can be used instead of capacitors --with the opposite characteristics, of course -but capacitors are generally used because they are free from hum-pickup troubles, and are usually much less expensive than inductors). Both circuits are essentially voltage dividers. In Fig 202-a the top resistive element (R1) is short-circuited at the highest frequencies by capacitor C u. Thus at the higher frequencies the output voltage nearly equals the input voltage, giving the effect of a high-frequency boost.
In Fig. 202-b the lower resistor (R2) is open-circuited at low frequencies by the capacitor CL. As the frequency is decreased, the reactance of CL rises. This reactance is in series with R2, consequently the signal voltage across this series combination goes up with a lowering of frequency.

Fig. 202. Basic R-C equalizer circuits. (a) high-end boost. (b) low-end
boost.
Two mistakes are commonly made in dealing with these circuits:
1. It is assumed that they produce ideal steps with a slope of 6 db per octave (an octave is a 2:1 frequency ratio), and that the turnover frequencies are exactly at the opposite ends of the step. The actual slopes are invariably less than 6 db, and the turnover points are never exactly at the ends.
2. The effects of the input and output impedances in the circuit where the equalizer is connected are neglected.
The most important actual characteristics of each circuit can be found by checking its response at three frequencies. Two of these are the turnover frequencies F1 and F2; the third (F3) is the geometric mid frequency F3 =- V F1 X F2. F3 is useful because the actual response curve has its steepest slope at this point.

Fig. 203. Equalization curve (insert), and chart for finding characteristics
with circuit combinations. "A" is over-all height of the step; "B" is
height of roll-off at each end of the step; "C" shows net boost
(or drop) between turnover frequencies F1 and F 2; "D" gives
maximum slope at the mid frequency point F3.
The insert in Fig. 203 is a generalized equalization curve showing the important factors. (Although this represents the performance of a high-frequency boost circuit -Fig. 202a) it can be applied just as well to bass-boost equalizers (Fig. 202-b) by simply reversing the curve.
Frequencies F1 and F0 are the "turnover" points of the curve.
The straight line A in Fig. 203 gives the relation between the over all height of the step and the ratio R1/RT or the ratio between the reference frequencies F1 and F2. Curve A has a uniform slope of 6 db per octave. Curve B show how much the response at the turnover frequencies F1 and F 2 departs from the nearest level portion of the over-all response curve; for big steps this is very nearly 3 db. Curve C shows the difference in response between the turnover frequencies F1 and F2; curve D gives the maximum slope in db per octave (at mid frequency F 3).

Fig. 204. Typical curves derived from Fig. 203. a, b, and c show the
separation between Fi and Fe . Note that the maximum slope is still less
than 6 db per octave.
Some typical solutions based on the use of this chart are shown in Fig. 204. In Fig. 204-a, for an over-all step height of 3 db, the turn over frequencies have a ratio 1.4/1 (half an octave). The maximum slope is about 1 db per octave, and there is only about 0.5 db difference in level between F1 and F 2. There is a rolloff of 1.25 db. between each of the turnover frequencies and the ultimate levels.
In Fig. 204-b, F1 and F 2 are separated by an octave; the maximum slope is 2 db per octave, and the difference in level between F1 and F 2 is nearly 2 db. There is a 2-db rolloff at each end.
In Fig. 204-c, F1 and F2 are separated by a decade (3.32 octaves or a 10:1 frequency ratio), giving a 20-db over-all step, and a 14-db difference between F 1 and F2. Even in this case the maximum slope is still less than 6 db per octave, and the average slope over the 10-to-1 frequency range is only 4.5 db per octave.
Terminal impedances
Now for the second source of error. If an equalizer designed according to the methods in the preceding section is connected between two existing amplifier stages, the results may not conform to expectations. The predicted response would be obtained if the equalizer input voltage was the same at all frequencies. Unfortunately, the input impedance changes with frequency, and so does the voltage. The grid-circuit impedance of the following stage also changes with frequency and affects the performance. These plate- and grid-circuit impedances must be included in the design calculations for the equalizer.

Fig. 205. (a) Complete h.f.-boost equalizer showing elements affecting
its characteristics. (b) Equivalent source impedance for finding l.f.
turnover point. (c) Equivalent circuit for finding h.f. turn over frequency.
High-end boost
Fig. 205 is the basic circuit of Fig. 202-a modified to include these source and output impedances. The low-end turnover frequency is found by making the reactance of CH equal to R1 . But the remaining resistance in the loop ( RT) is now R2 in series with the parallel combi nation of R (the plate resistance of V1) and the load resistance RL (Fig. 205-b). The high-frequency turnover, F2, is found by making the reactance of CH equal to the parallel combination of R1 and RT (Fig. 205-c). In practice it will only be necessary to find one of these frequencies. F1 is the easiest to calculate.

Fig. 206. (a) Low-frequency-boost equalizer. (b) Equivalent input impedance.
As an example in designing an equalizer, suppose that R p is 1.5 megohms, RL is 330,000 ohms, and R2 is 470,000 ohms. A high-frequency-boost step of 15 db is required between F i and F2, starting at a low-frequency turnover (F1) of 2,000 cycles. We can use the equivalent circuit in Fig. 205-b to find the value of RT. R, in parallel with RL gives about 280,000 ohms net plate-circuit resistance; this added to 470,000 ohms (R2) gives 750,000 ohms for R. A 15-db boost calls for a ratio R1 / RT of 4.6 (curve A in Fig. 203), so that RI works out to about 3.5 megohms. A standard value of 3.3 megohms would be close enough. The circuit will show a boost of 2.9 db (curve B in Fig. 203), when CH has a reactance of 3.3 megohms at 2,000 cycles (25 14). Now the grid-circuit impedance of V2 enters the picture. If the input capacitance ( CG), is 25 uuf, the total attenuation will be 6 db more than anticipated, because CH and CG form a 2-to-1 capacitive voltage divider at the highest frequencies. Using a smaller value for R2 will reduce the effect of CG. With R2 equal to 100,000 ohms, RT becomes 380,000 ohms. RI then works out to 1.75 megohms (standard value 1.8 megohms). CH would then be 50 Rtf for a 2,000-cycle low frequency turnover. With CG equal to 25 uuf, the added loss is only 3.5 db.
Increasing the over-all height of the step will offset this loss still further. Using a figure of 20 db, the ratio R1/RT will be 9, according to curve A in Fig. 203. R1 works out to 9 x 380,000, or about 3.3 meg ohms, which again calls for CH = 25 uuf to lift at 2,000 cycles. The loss due to CG will be 6 db, leaving a net step height of 20 -6, or 14 db.
In any case it pays to reduce the V2 input capacitance to the smallest possible value. One method is to develop a large amount of inverse feedback in V2 by using an unbypassed cathode resistor, or by operating V2 as a cathode follower.
Bass-boost circuit

Fig. 207. Workable form of l.f.-boost equalizer, with d.c. return to
ground.

Fig. 208. Another form of low-frequency boost equalizer. R3 may be a
variable resistor for controlling the response.
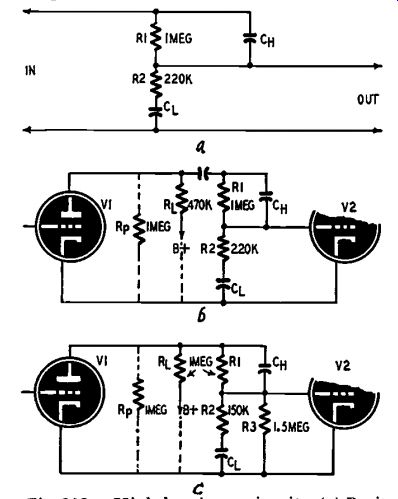
Fig. 209. High-low-boost circuit. (a) Basic network. (b) Input and output
circuits added. (c) Compensation for equal high and low boost by adding
R3.
Now let us turn to the bass-boost equalizer following the basic circuit of Fig. 202-b. Input- and output-impedance factors are shown in Fig. 206. Here R2 is in series with CL (Fig. 206-a) and the balance of the circuit is the series-parallel combination shown in Fig. 206-b. Fig. 206-a would not work in practice because the V2 grid circuit has no d.c. return to ground. Two workable arrangements are shown in Figs. 207 and 208, and the equivalent basic derivation is given under each.
In Fig. 207, R3 shunts all the other elements (R2 is effectively open-circuited by CL). This is obviously the simplest circuit to use. Fig. 208 is better where adjustable boost is required.
Turning back to the question of the errors arising from failure to take circuit impedances into account, take the example shown in Fig. 209.
This network is intended to boost both ends of the frequency range.
The values of R1 and R2 in the basic circuit of Fig. 209-a should give a lift of about 14 db at each end. If this arrangement is merely inserted between two stages, as in Fig. 209-b (ignoring for the moment the need for a d.c. grid return), the plate-circuit impedance of V1 will reduce the h.f. boost and increase the bass boost, throwing the whole arrangement off balance. With the values shown in Fig. 209-b, the plate circuit resistance consisting of RL and R., in parallel is about 330,000 ohms; using the equivalent circuit of Fig. 205-b we find that RT is 550,000 ohms, so the ratio R1/R is only about 2. Consulting curve A in Fig. 203 we see that this gives less than 10 db top lift (ignoring possible effects due to input capacitance). For bass lift in Fig. 209-b, the increased reactance of CL to over 3 megohms makes R1/RT about 6, giving nearly 16 db lift.
By careful choice of values in the circuit of Fig. 209-c, using the equivalents shown in Figs. 206 and 208, R3 will not affect the top lift materially, but its value can be adjusted to bring the bass boost to the required equal value. The values shown will give 14 db lift at each end. The reactances of capacitors CH and CL must be equal to R1 and R2 respectively at the high and low turnover frequencies. To avoid confusion the effect of grid input capacitance has been ignored; to include it, the procedure for designing the top lift will be as in the earlier example, after which the bass lift can be adjusted by R3 as just stated.