AUDIBILITY OF DISTORTION
Harmonic and intermodulation distortions
Because of the small dissipations which are normally involved, almost all discrete component voltage amplifier circuitry will operate in class '?' (that condition in which the bias applied to the amplifying device is such as to make it operate in the middle of the linear region of its input/output transfer characteristic), and the residual harmonic components are likely to be mainly either second or third order, which are audibly much more tolerable than higher order distortion components.
Experiments in the late 1940s suggested that the level of audibility for second and third harmonics was of the order of 0.6% and 0.25% respectively, and this led to the setting of a target value, within the audio spectrum, of 0.1% THD, as desirable for high quality audio equipment.
However, recent work aimed at discovering the ability of an average listener to detect the presence of low order (i.e. second or third) harmonic distortions has drawn the uncomfortable conclusion that listeners, taken from a cross section of the public, may rate a signal to which 0.5% second harmonic distortion has been added as 'more musical' than, and therefore preferable to, the original undistorted input. This discovery tends to cast doubt on the value of some subjective testing of equipment.
What is not in dispute is that the inter-modulation distortion, (IMD), which is associated with any non-linearity in the transfer characteristics, leads to a muddling of the sound picture, so that if the listener is asked, not which sound he prefers, but which sound seems to him to be the clearer, he will generally choose that with the lower harmonic content.
The way in which IMD arises is shown in FIG. 26, where a composite signal containing both high-frequency and low-frequency components, fed through a non-linear system, causes each signal to be modulated by the other. This is conspicuous in the drawing in respect of the HF component, but is also true for the LF one.
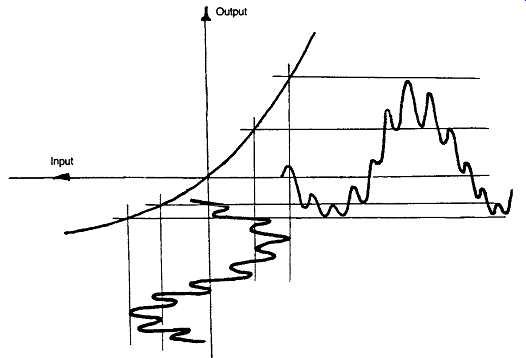
FIG. 26 Inter-modulation distortions produced by the effect of a nonlinear
input/output transfer characteristic on a complex tone.
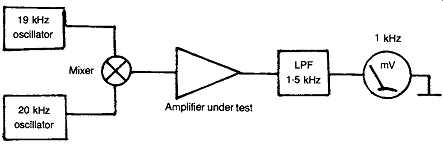
FIG. 27 Simple HF two-tone inter-modulation distortion test.
This can be shown mathematically to be due to the generation of sum and difference products, in addition to the original signal components, and provides a simple method, shown schematically in FIG. 27 , for the detection of this type of defect. A more formal IMD measurement system is shown in FIG. 28.
With present circuit technology and device types, it’s customary to design for total harmonic and IM distortions to be below 0.01% over the range 30 Hz-20 kHz, and at all signal levels below the onset of clipping.
Linear IC op. amps, such as the TL071 and the LF351, will also meet this spec, over the frequency range 30 Hz-10 kHz.
Transient defects
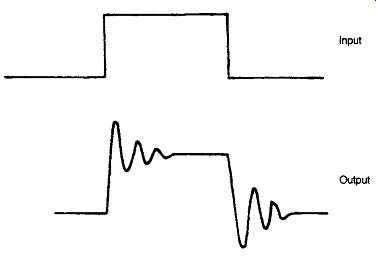
A more insidious group of signal distortions may occur when brief signals of a transient nature, or sudden step type changes in base level, are superimposed on the more continuous components of the program signal. These defects can take the form of slew-rate distortions, usually associated with loss of signal during the period of the slew-rate saturation of the amplifier - often referred to as transient inter-modulation distortion or TID. This defect is illustrated in FIG. 29, and arises particularly in amplifier systems employing substantial amounts of negative feedback, when there is some slew-rate limiting component within the amplifier, as shown in FIG. 30.

FIG. 28 Two-tone inter-modulation distortion test rig.
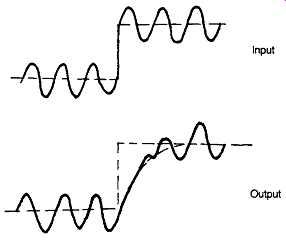
FIG. 29 Effect of amplifier slew-rate saturation or transient intermodulation
distortion.
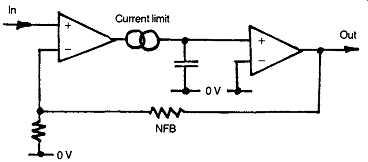
FIG. 30 Typical amplifier layout causing slew-rate saturation.
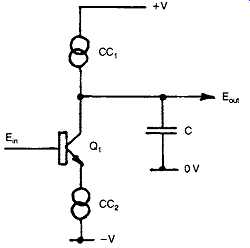
FIG. 32 Circuit design aspects which may cause slew-rate limiting.
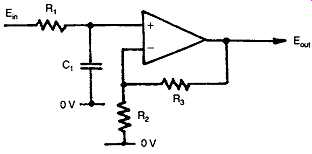
FIG. 33 Input HF limiting circuit to lessen slew-rate limiting.
A further problem is that due to 'overshoot', or 'ringing', on a transient input, as illustrated in FIG. 31. This arises particularly in feedback amplifiers if there is an inadequate stability margin in the feedback loop, particularly under reactive load conditions, but will also occur in low-pass filter systems if too high an attenuation rate is employed.
The ear is very sensitive to slew-rate induced distortion, which is perceived as a 'tizziness' in the reproduced sound. Transient overshoot is normally noted as a somewhat over-bright quality. The avoidance of both these problems demands care in the circuit design, particularly when a constant current source is used, as shown in FIG. 32.
In this circuit, the constant current source, CQ, will impose an absolute limit on the possible rate of change of potential across the capacitance Q, (which could well be simply the circuit stray capacitance), when the output voltage is caused to move in a positive-going direction. This problem is compounded if an additional current limit mechanism, CC2, is included in the circuitry to protect the amplifier transistor (Qj) from output current overload.
Since output load and other inadvertent capacitances are unavoidable, it’s essential to ensure that all such current limited stages operate at a current level which allows potential slewing to occur at rates which are at least 10x greater than the fastest signal components. Alternatively, means may be taken, by way of a simple input integrating circuit, (R1C1), as shown in FIG. 33, to ensure that the maximum rate of change of the input signal voltage is within the ability of the amplifier to handle it.
Spurious signals
In addition to harmonic, IM, and transient defects in the signal channel, which will show up on normal instrumental testing, there is a whole range of spurious signals which may not arise in such tests. The most common of these is that of the intrusion of noise and alien signals, either from the supply line, or by direct radio pick-up.
This latter case is a random and capricious problem which can only be solved by steps appropriate to the circuit design in question. However, supply line intrusions, whether due to unwanted signals from the power supply, or from the other channel in a stereo system, may be greatly reduced by the use of circuit designs offering a high immunity to voltage fluctuations on the DC supply.
Other steps, such as the use of electronically stabilized DC supplies, or the use of separate power supplies in a stereo amplifier, are helpful, but the required high level of supply line signal rejection should be sought as a design feature before other palliatives are applied.
Modern IC opamps offer a typical supply voltage rejection ratio of 90 dB (30000:1). Good discrete component designs should offer at least 80 dB (10000:1). This figure tends to degrade at higher frequencies, and this has led to the growing use of supply line bypass capacitors having a low effective series resistance (ESR). This feature is either a result of the capacitor design, or is achieved in the circuit by the designer's adoption of groups of parallel connected capacitors chosen so that the AC impedance remains low over a wide range of frequencies.
A particular problem in respect of spurious signals, which occurs in audio power amplifiers, is due to the loudspeaker acting as a voltage generator, when stimulated by pressure waves within the cabinet, and injecting unwanted audio components directly into the amplifier's negative feedback loop. This specific problem is unlikely to arise in small signal circuitry, but the designer must consider what effect output/line load characteristics may have - particularly in respect of reduced stability margin in a feedback amplifier.
In all amplifier systems there is a likelihood of microphonic effects due to the vibration of the components. This is likely to be of increasing importance at the input of 'low level', high sensitivity, pre-amplifier stages, and can lead to coloration of the signal when the equipment is in use, which is overlooked in the laboratory in a quiet environment.
Mains-borne interference
Mains-borne interference, as evidenced by noise pulses on switching electrical loads, is most commonly due to radio pick-up problems, and is soluble by the techniques (attention to signal and earth line paths, avoidance of excessive HF bandwidth at the input stages) which are applicable to these.
GENERAL DESIGN CONSIDERATIONS
During the past three decades, a range of circuit design techniques has been evolved to allow the construction of highly linear gain stages based on bipolar transistors whose input characteristics are, in themselves, very non-linear. These techniques have also allowed substantial improvements in possible stage gain, and have led to greatly improved performance from linear, but low gain, field-effect devices.
These techniques are used in both discrete component designs and in their monolithic integrated circuit equivalents, although, in general, the circuit designs employed in linear ICs are considerably more complex than those used in discrete component layouts.
This is partly dictated by economic considerations, partly by the requirements of reliability, and partly because of the nature of IC design.
The first two of these factors arise because both the manufacturing costs and the probability of failure in a discrete component design are directly proportional to the number of components used, so the fewer the better, whereas in an IC, both the reliability and the expense of manufacture are only minimally affected by the number of circuit elements employed.
In the manufacture of ICs, as has been indicated above, some of the components which must be employed are much worse than their discrete design equivalents. This has led the IC designer to employ fairly elaborate circuit structures, either to avoid the need to use a poor quality component in a critical position, or to compensate for its shortcomings.
Nevertheless, the ingenuity of the designers, and the competitive pressures of the market place, have resulted in systems having a very high performance, usually limited only by their inability to accept differential supply line potentials in excess of 36 V, unless non-standard diffusion processes are employed.
For circuitry requiring higher output or input voltage swings than allowed by small signal ICs, the discrete component circuit layout is, at the moment, unchallenged. However, as every designer knows, it’s a difficult matter to translate a design which is satisfactory at a low working voltage design into an equally good higher voltage system.
This is because:
• increased applied potentials produce higher thermal dissipations in the components , for the same operating currents;
• device performance tends to deteriorate at higher inter-electrode potentials and higher output voltage excursions;
• available high/voltage transistors tend to be more restricted in variety and less good in performance than lower voltage types.
CONTROLS
These fall into a variety of categories:
• gain controls needed to adjust the signal level between source and power amplifier stages
• tone controls used to modify the tonal characteristics of the signal chain
• filters employed to remove unwanted parts of the incoming signal, and those adjustments used to alter the quality of the audio presentation, such as stereo channel balance or channel separation controls.

FIG. 34 Standard gain control circuit.
Gain controls
These are the simplest in basic form, and are often just a resistive potentiometer voltage divider of the type shown in FIG. 34. Although simple, this component can generate a variety of problems. Of these, the first is that due to the value chosen for Rle Unless this is infinitely high, it will attenuate the maximum signal voltage, (Emax), obtainable from the source, in the ratio
E_max = En x Ri/(Ri + Z_source)
where Z_source is the output impedance of the driving circuit. This factor favors the use of a high value for Ru to avoid loss of input signal.
However, the following amplifier stage may have specific input impedance requirements, and is unlikely to operate satisfactorily unless the output impedance of the gain control circuit is fairly low. This will vary according to the setting of the control, between zero and a value, at the maximum gain setting of the control, due to the parallel impedances of the source and gain control.
A>ut = Ri'(Ri "· " zsource>)
The output impedance at intermediate positions of the control varies as the effective source impedance and the impedance to the 0 V line is altered. However, in general, these factors would encourage the use of a low value for Rx.
An additional and common problem arises because the perceived volume level associated with a given sound pressure (power) level has a logarithmic characteristic. This means that the gain control potentiometer, R], must have a resistance value which has a logarithmic, rather than linear, relationship with the angular rotation of the potentiometer shaft.

FIG. 35 Improved gain control using multi-pole switch.
POTENTIOMETER LAW
Since the most common types of control potentiometer employ a resistive composition material to form the potentiometer track, it’s a difficult matter to ensure that the grading of conductivity within this material will follow an accurate logarithmic law.
On a single channel this error in the relationship between signal loudness and spindle rotation may be relatively unimportant. In a stereo system, having two ganged gain control spindles, intended to control the loudness of the two channels simultaneously, errors in following the required resistance law, existing between the two potentiometer sections, will cause a shift in the apparent location of the stereo image as the gain control is adjusted, and this can be very annoying.
In high-quality equipment, this problem is sometimes avoided by replacing Rx by a precision resistor chain (Ra-Rz), as shown in FIG. 35, in which the junctions between these resistors are connected to tapping points on a high-quality multi-position switch.
By this means, if a large enough number of switch tap positions is available, and this implies at least a 20-way switch to give a gentle gradation of sound level, a very close approximation to the required logarithmic law can be obtained, and two such channel controls could be ganged without unwanted errors in differential output level.
CIRCUIT CAPACITANCES
A further practical problem, illustrated in FIG. 34, is associated with circuit capacitances. Firstly, it’s essential to ensure that there is no standing DC potential across Kx in normal operation, otherwise this will cause an unwanted noise in the operation of the control. This imposes the need for a protective input capacitor, and this will cause a loss of low frequency signal components, with a - 3 dB LF turn-over point at the frequency at which the impedance of Q is equal to the sum of the source and gain control impedances. Q should therefore be of adequate value.
Additionally, there are the effects of the stray capacitances, C2 and C3, associated with the potentiometer construction, and the amplifier input and wiring capacitances, C4. The effect of these is to modify the frequency response of the system, at the HF end, as a result of signal currents passing through these capacitances. The choice of a low value for R^ is desirable to minimize this problem.
The use of the gain control to operate an on/off switch, which is fairly common in low-cost equipment, can lead to additional problems, especially with high resistance value gain control potentiometers, in respect of AC mains 'hum' pick up. It also leads to a more rapid rate of wear of the gain control, in that it’s rotated at least twice whenever the equipment is used.
Tone controls
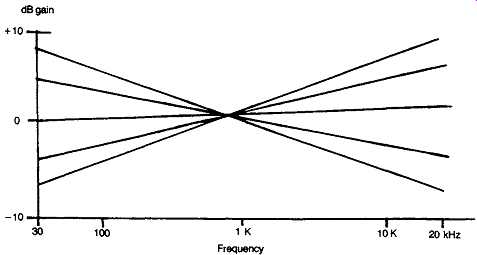
These exist in the various forms shown in Figs 36-40, respectively described as standard (bass and treble lift or cut), slope control, Clapham Junction, parametric and graphic equalizer types. The effect these will have on the frequency response of the equipment is shown in the drawings, and their purpose is to help remedy shortcomings in the source program material, the receiver or transducer, or in the loudspeaker and listening room combination.
To the hi-fi purist, all such modifications to the input signal tend to be regarded with distaste, and are therefore omitted from some hi-fi equipment. However, they can be useful, and make valuable additions to the audio equipment, if used with care.
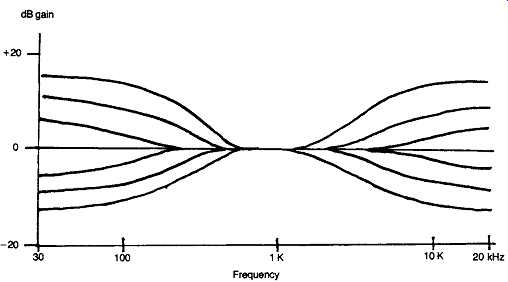
FIG. 36 Bass and treble lift/cut tone control.
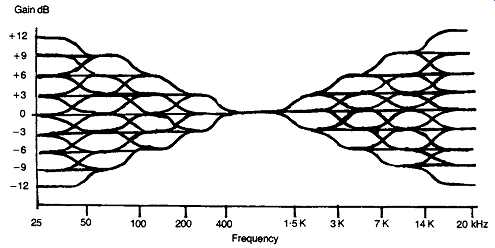
FIG. 38 Clapham Junction type of tone control.
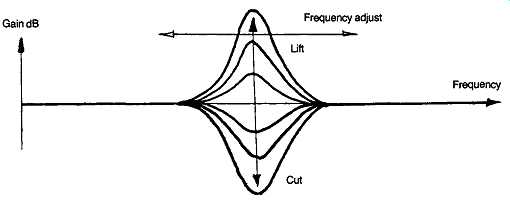
FIG. 39 Parametric equalizer control.
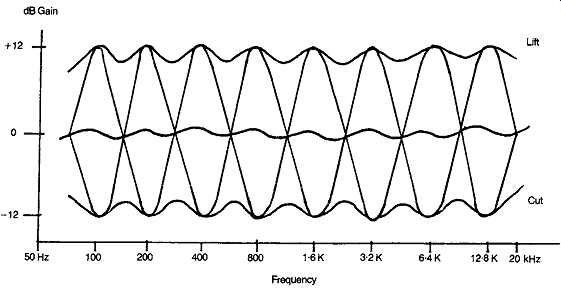
FIG. 40 Graphic equalizer response characteristics.
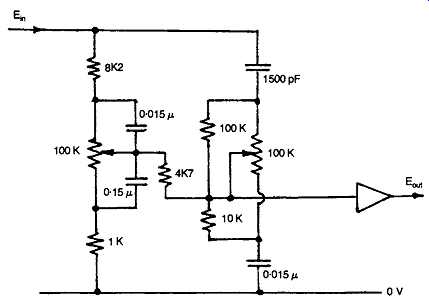
FIG. 41 Circuit layout of passive tone control.
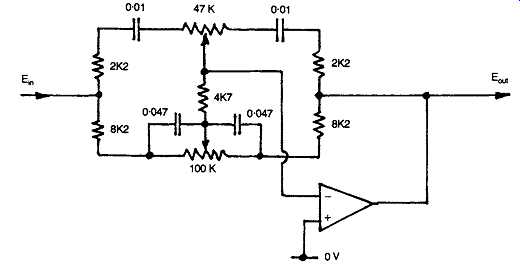
FIG. 42 Negative feedback type tone control circuit.
STANDARD TONE CONTROL SYSTEMS
These are either of the passive type, of which a typical circuit layout is shown in FIG. 41, or are constructed as part of the negative feedback loop around a gain block, using the general design due to Baxandall. A typical circuit layout for this kind of design is shown in FIG. 42.
It’s claimed that the passive layout has an advantage in quality over the active (feedback network) type of control, in that the passive network merely contains resistors and capacitors, and is therefore free from any possibility of introduced distortion, whereas the 'active' network requires an internal gain block, which is not automatically above suspicion.
In reality, however, any passive network must introduce an attenuation, in its flat response form, which is equal to the degree of boost sought at the maximum 'lift' position, and some external gain block must therefore be added to compensate for this gain loss.
This added gain block is just as prone to introduce distortion as that in an active network, with the added disadvantage that it must provide a gain equal to that of the flat-response network attenuation, whereas the active system gain block will typically have a gain of unity in the flat response mode, with a consequently lower distortion level.
As a final point, it should be remembered that any treble lift circuit will cause an increase in harmonic distortion, simply because it increases the gain at the frequencies associated with harmonics, in comparison with that at the frequency of the fundamental.
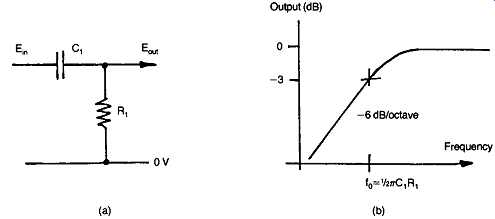
FIG. 43 Layout and frequency response of simple bass-cut circuit (high-pass).
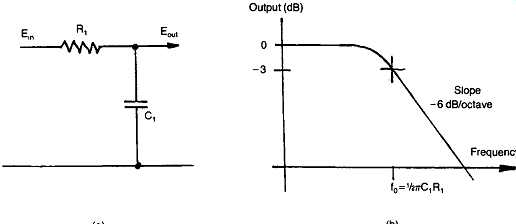
FIG. 44 Layout and frequency response of simple treble-cut circuit (low-pass).
The verdict of the amplifier designers appears to be substantially in favor of the Baxandall system, in that this is the layout most commonly employed.
Both of these tone control systems - indeed this is true of all such circuitry - rely for their operation on the fact that the AC impedance of a capacitor will depend on the applied frequency, as defined by the equation:
Zc = 1/(2 π fc),
or more accurately,
Zc = 1/(2 j π fc),
where j is the square root of -1.
Commonly, in circuit calculations, the 2πf group of terms are lumped together and represented by the Greek symbol ‘w’ (omega). The purpose of the j term, which appears as a 'quadrature' element in the algebraic manipulations, is to permit the circuit calculations to take account of the 90° phase shift introduced by the capacitative element. (The same is also true of inductors within such a circuit, except that the phase shift will be in the opposite sense.) This is important in most circuits of this type.
The effect of the change in impedance of the capacitor on the output signal voltage from a simple RC network, of the kind shown in Figs 43(a) and 44(a), is shown in Figs 43(b) and 44(b). If a further resistor, R2, is added to the networks the result is modified in the manner shown in Figs 45 and 46. This type of structure, elaborated by the use of variable resistors to control the amount of lift or fall of output as a function of frequency, is the basis of the passive tone control circuitry of FIG. 41.
If such networks are connected across an inverting gain block, as shown in Figs 47(a) and 48(a), the resultant frequency response will be shown in Figs 47(b) and 48(b), since the gain of such a negative feedback configuration will be:
Gain = Za/Zb
…assuming that the open-loop gain of the gain block is sufficiently high.
This is the design basis of the Baxandall type of tone control, and a flat frequency response results when the impedance of the input and output limbs of such a feedback arrangement remains in equality as the frequency is varied.
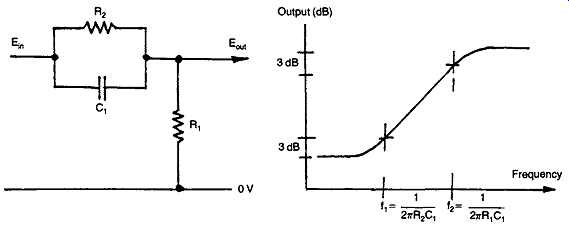
FIG. 45 Modified bass-cut (high-pass) RC circuit.
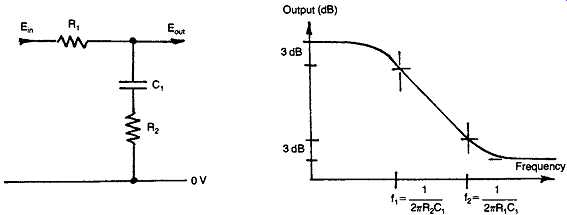
FIG. 46 Modified treble-cut (low-pass) RC circuit.
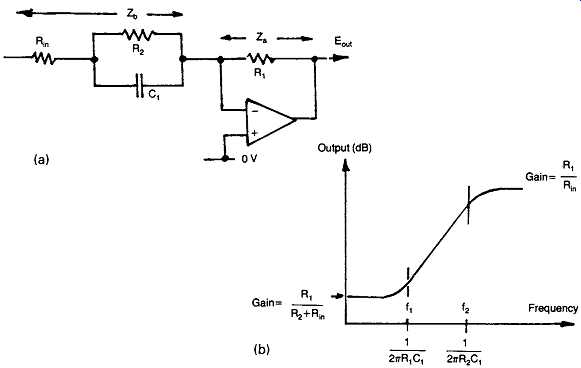
FIG. 47 Active RC treble-lift or bass-cut circuit.
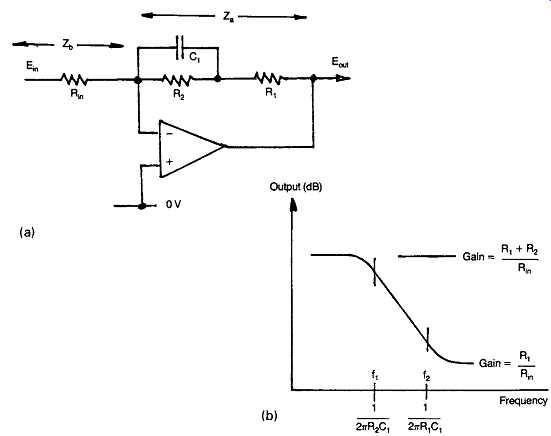
FIG. 48 Active RC treble-cut or bass-lift circuit.
SLOPE CONTROLS
This is the type of tone control employed by Quad in its type 44 preamplifier, and operates by altering the relative balance of the LF and HF components of the audio signal, with reference to some specified midpoint frequency, as is shown in FIG. 37. A typical circuit for this type of design is shown in FIG. 49.
The philosophical justification for this approach is that it’s unusual for any commercially produced program material to be significantly in error in its overall frequency characteristics, but the tonal preferences of the recording or broadcasting balance engineer may differ from those of the listener.
In such a case, he might consider that the signal, as presented, was somewhat over heavy, in respect of its bass, or alternatively, perhaps, that it was somewhat light or thin in tone, and an adjustment of the skew of the frequency response could correct this difference in tonal preference without significantly altering the signal in other respects.
THE CLAPHAM JUNCTION TYPE
This type of tone control, whose possible response curves are shown in FIG. 38, was introduced by the author to provide a more versatile type of tonal adjustment than that offered by the conventional standard systems , for remedying specific peaks or troughs in the frequency response, without the penalties associated with the graphic equalizer type of control, described below.
In the Clapham Junction type system, so named because of the similarity of the possible frequency response curves to that of railway lines, a group of push switches is arranged to allow one or more of a multiplicity of RC networks to be introduced into the feedback loop of a negative feedback type tone control system, as shown in FIG. 50, to allow individual ±3 dB frequency adjustments to be made, over a range of possible frequencies.
By this means, it’s possible by combining elements of frequency lift or cut to choose from a variety of possible frequency response curves, without losing the ability to attain a linear frequency response.
PARAMETRIC CONTROLS
This type of tone control, whose frequency response is shown in FIG. 39, has elements of similarity to both the standard bass/treble lift/cut systems, and the graphic equalizer arrangement, in that while there is a choice of lift or cut in the frequency response, the actual frequency at which this occurs may be adjusted, up or down, in order to attain an optimal system frequency response.
A typical circuit layout is shown in FIG. 51.
THE GRAPHIC EQUALIZER SYSTEM
The aim of this type of arrangement is to compensate fully for the inevitable peaks and troughs in the frequency response of the audio system -- including those due to deficiencies in the loudspeakers or the listening room acoustics -- by permitting the individual adjustment of the channel gain, within any one of a group of eight single-octave segments of the frequency band, typically covering the range from 80 Hz to 20 kHz, though ten octave equalizers covering the whole audio range from 20 Hz to 20 kHz have been offered.
Because the ideal solution to this requirement - that of employing a group of parallel connected amplifiers, each of which is filtered so that it covers a single octave band of the frequency spectrum, whose individual gains could be separately adjusted - would be excessively expensive to implement, conventional practice is to make use of a series of LC tuned circuits, connected within a feedback control system, as shown in Fig. 52.
This gives the type of frequency response curve shown in FIG. 40. As can be seen, there is no position of lift or cut, or combination of control settings, which will permit a flat frequency response, because of the interaction, within the circuitry, between the adjacent octave segments of the pass-band.
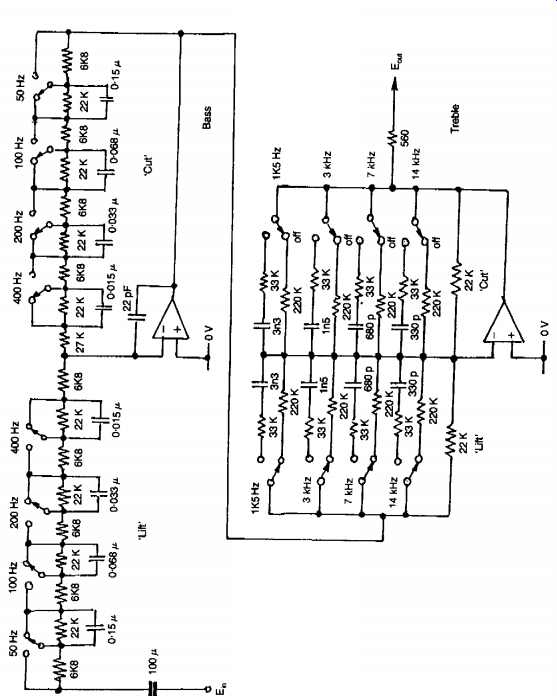
FIG. 50 Clapham Junction tone control.

FIG. 51 Parametric equalizer circuit.
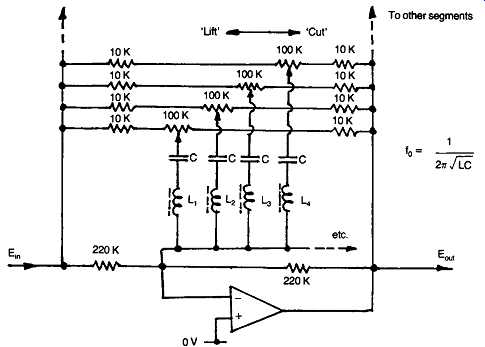
FIG. 52 Circuit layout for graphic equalizer (four sections only shown).
While such types of tone control are undoubtedly useful, and can make significant improvements in the performance of otherwise unsatisfactory hi-fi systems, the inability to attain a flat frequency response when this is desired, even at the mid-position of the octave-band controls, has given such arrangements a very poor status in the eyes of the hi-fi fraternity.
This unfavorable opinion has been reinforced by the less than optimal performance offered by inexpensive, add-on, units whose engineering standards have reflected their low purchase price.
Channel balance controls
These are provided in any stereo system, to equalize the gain in the left- and right-hand channels, to obtain a desired balance in the sound image. (In a quadraphonic system, four such channel gain controls will ideally be provided.) In general, there are only two options available for this purpose: those balance controls which allow one or other of the two channels to be reduced to zero output level, and those systems, usually based on differential adjustment of the amount of negative feedback across controlled stages, in which the relative adjustment of the gain, in one channel with reference to the other, may only be about 10 dB. This is adequate for all balance correction purposes, but does not allow the complete extinction of either channel.
The first type of balance control is merely a gain control, of the type shown in FIG. 34. A negative feedback type of control is shown in FIG. 53.
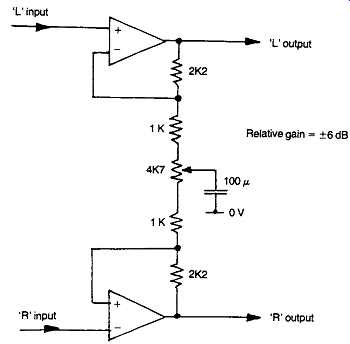
FIG. 53 Negative feedback type channel balance control.
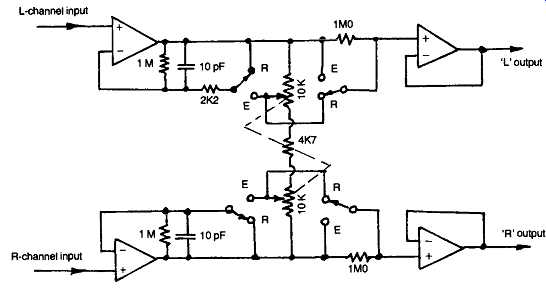
FIG. 54 Circuit for producing enhanced or reduced stereo channel separation.
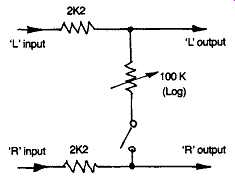
FIG. 55 Simple stereo channel blend control.

FIG. 56 Channel separation or blending by using matrix addition or subtraction.
Channel separation controls
While the closest reproduction, within the environment of the listener, of the sound stage of the original performance will be given by a certain specific degree of separation between the signals within the 'L' and 'R' channels, it’s found that shortcomings in the design of the reproducing and amplifying equipment tend universally to lessen the degree of channel separation, rather than the reverse.
Some degree of enhancement of channel separation is therefore often of great value, and electronic circuits for this purpose are available, such as that, due to the author, shown in FIG. 54.
There are also occasions when a deliberate reduction in the channel separation is of advantage, as , for example, in lessening 'rumble' effects due to the vertical motion of a poorly engineered record turntable, or in lessening the hiss component of a stereo FM broadcast. While this is also provided by the circuit of FIG. 54, a much less elaborate arrangement, as shown in FIG. 55, will suffice for this purpose.
A further, and interesting, approach is that offered by Blumlein, who found that an increase or reduction in the channel separation of a stereo signal was given by adjusting the relative magnitudes of the 'L+R' and 'L-R' signals in a stereo matrix, before these were added or subtracted to give the '2L' and '2R' components.
An electronic circuit for this purpose is shown in FIG. 56.

FIG. 57 Steep-cut filter circuits.
Filters
While various kinds of filter circuit play a very large part in the studio equipment employed to generate the program material, both as radio broadcasts and as recordings on disc or tape, the only types of filter normally offered to the user are those designed to attenuate very low frequencies, below, say, 50 Hz and generally described as 'rumble' filters, or those operating in the region above a few kHz, and generally described as 'scratch' or 'whistle' filters.
Three such filter circuits are shown in Figs 57(a), (b), and (c). Of these the first two are fixed frequency active filter configurations employing a bootstrap type circuit , for use respectively in high-pass (rumble) and low-pass (hiss) applications, and the third is an inductor-capacitor passive circuit layout, which allows adjustment of the HF turn-over frequency by variation of the capacitor value.
Such frequency adjustments are, of course, also possible with active filter systems, but require the simultaneous switching of a larger number of components. For such filters to be effective in their intended application, the slope of the response curve, as defined as the change in the rate of attenuation as a function of frequency, is normally chosen to be high - at least 20 dB/octave - as shown in FIG. 58, and, in the case of the filters operating in the treble region, a choice of operating frequencies is often required, as is also, occasionally, the possibility of altering the attenuation rate.
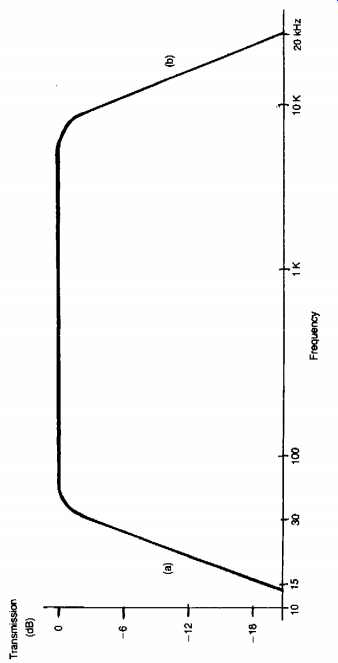
FIG. 58 Characteristics of circuits of Figs 57(a) and (b).
This is of importance, since rates of attenuation in excess of 6 dB/octave lead to some degree of coloration of the reproduced sound, and the greater the attenuation rate, the more noticeable this coloration becomes.
This problem becomes less important as the turn-over frequency approaches the limits of the range of human hearing, but very steep rates of attenuation produce distortions in transient waveforms whose major frequency components are much lower than notional cut-off frequency.
It is, perhaps, significant in this context that recent improvements in compact disc players have all been concerned with an increase in the sampling rate, from 44.1 kHz to 88.2 kHz or 176.4 kHz, to allow more gentle filter attenuation rates beyond the 20 kHz audio pass-band, than that provided by the original 21 kHz 'brick wall' filter.
The opinion of the audiophiles seems to be unanimous that such CD players, in which the recorded signal is two- or four-times 'oversampled', which allows much more gentle 'anti-aliasing' filter slopes, have a much preferable HF response and also have a more natural, and less prominent, high-frequency characteristic, than that associated with some earlier designs.