The realization of general coverage, multi-conversion receivers has brought about the need for a better understanding of their performance. In a radio receiver, mixers used to perform conversions are not only frequency adding and subtracting mechanisms, but they also exhibit a variety of undesired output products, in addition to their sum and difference frequencies. These are called intermodulation products. This phenomenon is complicated by the increased front-end bandwidth requirement (general coverage) as well as by the intermediate frequency i-f bandwidth requirement. If a multi-mixer situation exists, such as in a multi-conversion receiver, the problem is further aggravated, as initial unwanted products from one mixer can combine with those of another, creating a multitude of "birdies" at the final i-f output.
'Technical jargon used for unwanted interference which sounds like the whistling of a bird.
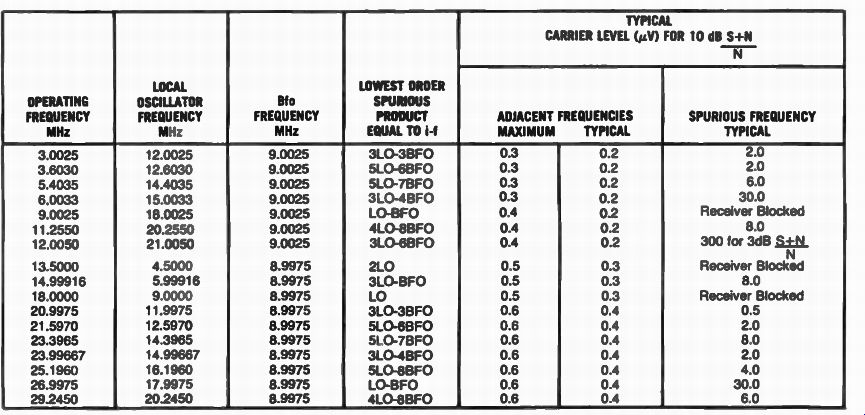
Table 1

Fig. 1. This dedicated receiver is intended for WWV reception on
one of the four selected frequencies. Automatic scanning of the receiving
frequencies allows the unit to determine which frequency has the most
usable signal and locks onto it. Careful system design shows that a double-conversion
approach was used having the first i-f at 45 MHz followed by a second
i-f at 4.6 MHz.
UNDERSTANDING INTERMODULATION PRODUCTS
The chart in Table 1 shows products generated at the output of a single-conversion general coverage communications receiver using a 9 MHz i-f. These products will interfere with received frequencies to the degree shown.
Whether a receiver is a dedicated type as the one shown in Fig. 1, or a general coverage type such as the one shown in Fig. 2, the problem of intermodulation products has to be carefully understood and weighed against system parameters, so a minimum number of "birdies" will be internally generated and heard within the pass-band of the receiver.
'Method of generalizing all cases so a single chart can be applied for finding a function.

Fig. 2. The Cubic model HF-1030 general coverage communications receiver
is used in a dual frequency diversity mode in this rack mounted installation
(courtesy of Cubic Communications).
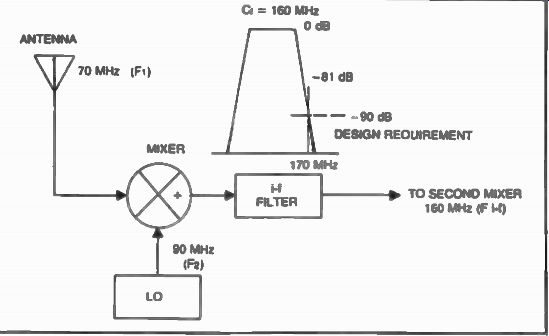
Fig. 3 Finding in-band intermodulation products dictates choice of
i-f center frequency as well as the shape factor of the i-f filter, in
order to meet system requirement.
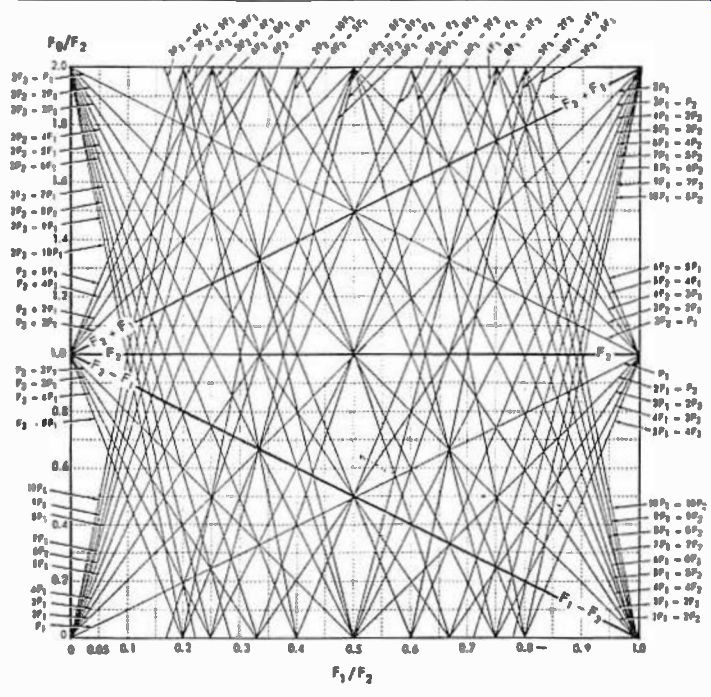
Fig. 4. Intermodulation products chart.
DESIGN TOOLS FOR PREDICTING INTERMODULATION DISTORTION (PRODUCT CHARTS AND THEIR USE)
Let's look at some analytical tools the system designer uses to deter mine these products. Let's assume we are going to design a fixed-frequency receiver for 70 MHz (Fig. 3). With a local oscillator of 90 MHz, the receiver will have a first i-f of 160 MHz if an up-conversion type is considered. The second conversion of this receiver is not discussed here in order to simplify this case. To find the two normalized* frequencies:
Fi 70 =0.778 F2 90 F(i-f) 160 =11.778 F 2 90
With this information and the mixer product chart in Fig. 4 find the locus point** for the two ratios, as shown in Fig. 5. The chart shows all products produced not only by the fundamentals, but also by multiples of the signal and oscillator frequencies which are present in the mixer stage, and correspond to the second, third, fourth, fifth, and sixth harmonics of the two mixing signals.
The order of the product is determined by the sum of the harmonic orders involved. For example, 5F1 +2 F 2 is a seventh order product (regardless of the mathematical operation involved) because it involves the fifth harmonic of F1 combined with the second harmonic of F2. Higher-order products are also present but they are usually of a sufficiently low level so as not to cause problems. Any line that crosses the locus point corresponds to a product which is identified on the edge of the chart.
**Intersection of a system of lines which satisfies one or m ore given conditions.

Table 2. Specifications of the ESM 500 Vhf/Uhf Receiver. (Continued
from page 72.)

Table 3. Intermodulation Product Chart Used for Mixers in an Adding
Mode (B+A) where A and B are the Mixing Frequencies and B • A. Ratios
A Are Shown for Each Intermodulation Product Up to the 15-th Order.

Table 4

Fig. 5. The intersection of the vertical and horizontal lines corresponding
tof1. F2 and E PA (locus point of normalized frequencies) indicates the
in-band inter modulation products. The out-of-band spurious outputs which
happen to be in the vicinity of the i-f frequency can also be verified
by looking at the products adjacent to the locus point.

Fig. 6. The ESM 500 is a general purpose vhf/uhf receiver designed
for radio monitoring. This highly digital receiver features a fast synthesizer
with a resolution of 1 kHz, a memory that can store up to 24 frequencies,
and a built in i-f panoramic display. Careful system and circuit design
is visible throughout the receiver (courtesy of Rohde & Schwarz).
Values of F1 and F, can be substituted and the interference can be anticipated and avoided: If the locus point is examined closely, one can be assured that there are no in-band products in this case, but analyzing the areas adjacent to the locus point indicates some out-of-band spurs (un wanted products) which will have to be suppressed by the i-f filter to the level specified in the requirement. By knowing their order given by the chart, their predicted amplitude can be found (in our case 170 MHz). The 7th and 9th product (5F1 -2F2 and 5F2-4F1 ) is predicted to be 81 dB below the i-f level (typical manufacturer prediction). The i-f filter would have to attenuate 9 dB at 170 MHz to accomplish a system requirement of 90 dB as shown in Fig. 3. Table 2 gives the specifications for the E5M 500 vhf/uhf receiver. FIG. 6 shows this fine receiver.
A simpler method of finding these products can be achieved by using the charts in Tables 3 and 4. The chart shown in Table 3 is for mixers used in an adding mode (B + A) where A and B are the mixing frequencies and B>A. The chart shown in Table 4 is for mixers used in a subtracting mode (B-A) with the same conditions applying. If using the same example, and substituting F1 for A and F2 for B the same ratio can be obtained.
A 70
= - = - =0.778 2 B 90
We then use Table 3 since the mixer in our example operates in the adding mode, and find the corresponding products as indicated in Fig. 7 (5A - 2B and 5B - 4A). If the numerical values of A and B are inserted in these formulas, the same resultant values can be obtained with this method, which is usually preferred. If this receiver were not designed for a fixed frequency you can imagine what a job it could be to evaluate all the high-order products generated within such a scheme.

Fig. 7. The same results can be obtained as with our previous
example by using the intermodulation chart at A shown here. Ratio = 0.778
which points to a 7-th and 9-th order product (5A-2B and 5B-4A). B
USING COMPUTERS TO SUPPORT THE PRODUCT CHARTS (A TI-59 PROGRAM)
Today, computer programs are used successfully to predict these problems. The following example will describe the use of a TI-59 programmable calculator (Fig. 8) to perform this tedious task for our example. A listing of the program is also included for those wishing to try their own problems.
This program finds all combinations of (m x LO) ± (n x re and prints those frequencies that fall in the center of the i-f by actually indicating "=i-f" in the printout. Those frequencies that fall within the predetermined i-f bandwidth but are not exactly in the center are also reported in the printout by the indication "*BW" (Fig. 9). The sample program in Fig. 10 shows how our 70 MHz fixed-frequency receiver may be analyzed using this method.
If the 90 MHz LO is entered into the user-defined key A, the 70 MHz rf into B, the 160 MHz i-f into C and the i-f bandwidth we wish to analyze into D (50 MHz) a report is obtained by depressing key E', indicating that we are ready to run the program with the entered data as shown in Fig. 9. If a mistake occurred in the process of entering the information, new data can be entered by repeating the above process with no alteration to the actual program. We can now run our analysis, by depressing Key E. A complete list of products will be automatically printed as shown in Fig. 10. The process will take approximately four minutes to analyze all cases of m and n within the bandwidth of 50 MHz. This may seem to be a long time, but not if we compare the effort with that of the product chart in Fig. 4.

Fig. 8. The Tl-59 programmable calculator and a PC-100 printer-plotter
are used to analyze the intermodulation products that may exist in a
radio receiver.

Fig. 9. Depressing Key E' will print out all conditions entered by
the operator.

Fig. 10. Depressing Key E on the Tl-59 will run the intermodulation
product program within the specified conditions indicating the same problem
areas 5RF-2L0 and 5L0-4 RF as previously determined with the intermodulation
charts. Other problems are also indicated within the i-f bandpass but
are not considered in our example for reasons of simplicity.
This program can be recorded on two magnetic cards and could be used over and over again as necessary. For those equipped with a TI-59, Table 5 shows the actual listing of the intermodulation products program.
Partitioning (OP 17) is 479.59. Table 6 lists all necessary procedures for running the program.
The amplitude of the undesired products identified depends on their particular order number (m+n). Most products of the seventh order or higher will be at least 60 dB down from the i-f level, and are usually not considered to cause problems. Unless instructed differently, the program will automatically calculate all products to the twelfth order (6 x LO) ± (6 x rf) (no user inputs to A' and B' are required). If a different resolution is desired the two keys should be addressed accordingly. The execution time of this program is a direct function of the product order and the i-f bandwidth required by the user.

Table 5. Listing of the 11-59 Program for Intermodulation Products.
Partitioning is 479.59 (Program Courtesy of Frank Ferrin, Honeywell, Inc.).

Fig. 11. Communications receiver block diagram. The first i-f is
75 MHz and the second i-f is 9 MHz. A two-loop synthesizer is used to
provide rough and fine tuning.

Table 6. User Instructions for the TI-59 Intermodulation Products
Program.
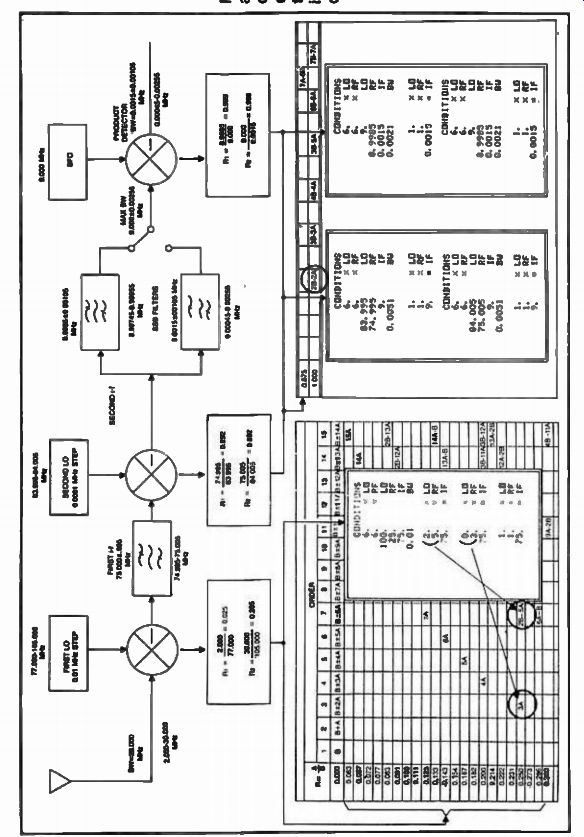
Fig. 12
SYSTEM ANALYSIS FOR A GENERAL COVERAGE COMMUNICATION RECEIVER (A DESIGN CASE)
In the following pages we will consider a system design for a general coverage receiver with a wide input bandwidth (28 MHz). Unlike the dedicated single frequency receiver analyzed in the previous pages, this wideband receiver presents an immense product analysis problem, which is due to the many different cases that could be created within the input bandwidth. The problem is further increased if a double-conversion approach is used, as products generated in the first i-f can multiply in the second i-f, as we discussed at the beginning of this Section. The designer should use good judgment in the initial choice of frequencies, since no computer or chart can take the place of good engineering procedures, as we will see in our example. Assume that a communication receiver is to be de signed that will cover the range of 2 MHz to 30 MHz, with good image rejection, and a minimum of unwanted products generated within its own configuration. Looking at Fig. 11 a double conversion approach is considered with an up-conversion first i-f compatible with commercially available monolithic crystal filters at 75 MHz. A phase-locked synthesizer is to be used as the local oscillator for the first mixer, and will provide rough tuning in 10 kHz steps over this range. The fine tuning is achieved in the second conversion with another synthesizer which provides frequency resolution of 100 Hz within the 10 kHz rough steps.
The second i-f is at 9 MHz because of the availability of good crystal lattice filters. Two sideband filters are used in this i-f. We will attempt to analyze the system shown with the help of the charts described earlier along with the TI-59 computer program which will perform the calculations necessary to support these charts.

Fig. 13. Tl-59 program indicates no intermodulation problem in the
second i-f of the double-conversion communications receiver. The -60
dB bandwidth (0.0374 MHz) of the filters was used for a worst-case analysis.
FIG. 12 shows the mathematical model for this receiver. An rf signal anywhere from 2.000 to 30.000 MHz comes from the antenna to the first mixer where it subtracts from the first local oscillator which operates so as to always produce a 75.000 MHz i-f. This local oscillator is our first synthesizer operating from 77.000 to 105.000 MHz in 0.01 MHz (10 kHz) steps. This dictates the bandwidth of the first i-f to be 10 kHz minimum, from 74.995 to 75.005 MHz in order for the second local oscillator to be able to provide fine tuning in the second i-f, as we previously discussed. The 75 MHz tandem monolithic filter (discussed earlier) is a practical example of a first i-f filter that could be used in this application. If rf = A and LO = B, two ratios A can be created: R minimum and R maximum.
2.000 12_ = 77.000 - 0.025 iv. 30.000 RmAx - 105.000
We will use the mixing product chart for subtraction since our i-f is 75 MHz, and find the entire affected band between RmiN and R.mAX as shown in Fig. 12. Any product indicated within this band could be a potential problem for the corresponding received frequency.
A look at our chart indicates a series of problems (7A, 6A, 5A, 4A, 3A, 2B-5A) with the worst one at 3A. If the TI-59 program is used, we can verify this case as shown in our example. At first we can say that the third harmonic of one of the two mixing signals could be quite powerful and could indeed produce a problem, but a closer look at the system indicates that the offending frequency A, is actually a received frequency and chances are very good that a distant 25 MHz station has a level of insignificant third harmonic (75 MHz) appearing at the antenna of our receiver.
The problem is further diminished by our receiver's preselector which greatly attenuates at 75 MHz. The same conditions apply to the other products indicated by the chart. They present even a better case since they are even further removed from the received frequencies. This is a case where engineering judgment is more important than all our tools which are only used to warn of possible problems. The case would be different, however, if the B signal was the offender. as 3B would have been the third harmonic of the local oscillator which can be of relatively high amplitude, and can cause interference.

Fig. 14. The 11-59 program indicates a 213-2A product within the
bandwidth of the 8 pole single sideband filters.
The filtered first i-f range of 74.995 to 75.005 MHz is further mixed with the second local oscillator operating in 0.0001 MHz (100 Hz) steps over the 10 kHz range of 83.995 to 84.005 MHz providing fine tuning for the receiver as we previously discussed. If R_mIN and R_mAx are found for the second i-f a new band of interest can be located on our' chart, as shown in Fig. 12.
74.995
R fdl = N 83.995 = 0.89285076
75.005
R = - 84.005 - 0.89286352 NIAX
Fig. 15. Bandwidth characteristics of the eight pole-single sideband filters used in the communications receiver. Sixteen-pole filters could be used to eliminate a 2B-2A audio product as well as to improve the total selectivity of the receiver.
Since the range to be covered is only 10 kHz, this band is very narrow and in reality is expressed by the same number (0.892) since the chart only extends to three decimal points. The i-f is centered at 9.000 MHz and its bandwidth is determined by the two single-sideband filters. For simplicity, the minimum corner frequency (- 3 dB) of the lower filter and the upper corner frequency for the higher filter were chosen determining a total bandwidth (-3 dB) of 0.0051 MHz (5.1 kHz, both sidebands). FIG. 12 indicates clearly that there is no problem except for a 13th order product which can be ignored, but since the band is so narrow and so close to the 1.000 ratio which presents quite a few problems, the computer is used to completely insure safety. Unless otherwise instructed, the program will not print out the 13th product as it is programmed to only calculate products to the 12th order. If the order is increased to 14, the computer will indicate that there is really not a case for 7A-6B (case shown in Fig. 12) within the ratio range.
Let's now proceed to analyze the second i-f in Fig. 12. A total bandwidth of 0.0374 MHz (37.4 kHz) is analyzed here to completely insure freedom from intermodulation products within the slopes of the 8-pole filters used in this i-f (37.4 kHz is the - 60 dB total bandwidth of the two filters) as shown in Fig. 13. It can be seen from this analysis that the charts can only be used to the guideline extent. For a more in-depth analysis, the TI-59 program or some other means of calculation has to be used to obtain precise answers.
We have determined that our system design provides a clean scheme to this point. The last conversion is from 9.000 MHz ± 0.00255 MHz to audio between 0.00045 to 0.00255 MHz (450 Hz to 2.550 kHz) in both single-sideband filter cases. The conversion takes place in a third mixer (product detector) as shown in our example (Fig. 14).
8.9985 Rmea 9.000 9.000 R = MAX 9 . 0015
= 0.999833
= 0.999833
These identical ratios locate the intermodulation band to be analyzed very close to the 1.000 ratio in the chart and with a -3 dB bandwidth of 0.0021 MHz (2.1 kHz). No problems are found for either one of the single-sideband filters. However, if the -60 dB bandwidth (0.0038 MHz) of the 8-pole filters is used for the TI-59 computer program, the 2B-2A problem circled in Fig. 12 becomes evident at the 3 kHz point in the slopes of our filters. This is true for either sideband filter as shown in Fig. 15 and the resulting audio distortion can only be cured by improving the shape factor of the filters, in our case by doubling the number of poles to 16 for each one of the single-sideband filters.
Another way to cure this problem would be to introduce a low-pass filter in the audio portion of our receiver which will cut off all frequencies beyond the 2.55 kHz which is the highest frequency passed by the filters. A practical cut-off point would be at 2.8 kHz. The first method is, however, preferred as it also provides better adjacent-channel rejection, improving upon the overall selectivity of the receiver.
This concludes the analysis for the double-conversion general coverage communications receiver. In performing this tedious task, we have scientifically proved that we have a thoroughly analyzed sound system, with a minimum of intermodulation problems. We can now proceed with confidence to the circuit design of our receiver. In conclusion, we can safely say that all frequency schemes used in communications receivers have un wanted products within their outputs, and the fact remains that any configuration chosen is simply the best compromise in the opinion of the designer.