ON THE MECHANICS OF TONEARMS PART 1: GENERAL PRINCIPLES AND STATIC BALANCE
With the resurgence of interest in LP playback, it's appropriate io explore some of the basic physical mechanics of tonearms.
Mechanics is a branch of physics that explores the behavior and analysis of moving masses and the forces associated with them. Applying the analysis of mechanics to tone arms is an essential part of tonearm de sign, but is often neglected outside of the design process. This has led to, among other things, a number of myths about how tonearms behave and the crucial factors affecting their behavior.
Here are some examples:
- When calculating the mass of a tone arm, you must add the tracking force.
- To reduce the effective mass, you should make the counterweight less massive.
Much of the analysis that follows makes some simplifying assumptions. For example, when we generally speak of a mass, we assume, for simplicity, that all of the mass is concentrated in one point, or at least in a region that is very small compared to the other dimensions of the problem. We also assume that all structures are rigid and all bearings are without friction. In most cases, the differences that result from these assumptions lead to analysis results that do not appreciably differ from physical reality, and are thus good models of that reality.
In other cases we will include the corrections due to masses actually occupying a large extent, and the effects of friction, because they can affect the behavior of the systems we are analyzing in nontrivial ways.
In no way do I intend this to be a comprehensive article on tonearm and turntable design. There are plenty of sources, many of them excellent, on various aspects of tonearm design. There are many articles on design factors to minimize tracking error and other aspects of geometry, RIAA preamplifier design, tonearm damping, and more.
Nor do I intend to preach a particular gospel even in the limited scope of the present topic: I am, for example, advocating neither high-arm mass or low-arm mass as being superior.
Rather, I present the basic physics behind why tonearms have the mass that they do, with the hope that armed with this information, you can better under stand the factors involved. Nowhere, necessarily, is there any information to be found here on how to design the very best arm; rather, I present the fundamentals needed to do that job. And also I hope that there's enough here to allow you to separate the important wheat from the advertising and mythological chaff that often surrounds discussions on LP playback principles.
A Question of Units
This discussion uses the metric system of units, throughout; more specifically, the cgs system (centimeters, grams, and seconds). The metric system of units allows for easy and consistent units calculation On the other hand, the normal "imperial" units have little logical relation to one another and are, indeed, a source of great confusion.
The basic unit of length or distance is the centimeter, (cm), which is a little more than 3% of an inch. From that, area is measured in cm? and volume in cm.
The basic unit of mass, a measurement of the amount of matter, is a gram, with about 28 grams in a dry ounce. You might find it curious that a single cubic centimeter of water has a mass of almost precisely 1g. In fact, a gram was initially defined as the mass of 1 cm? of water at its maximum density, at about 2°C.
Of course, the unit of time is the second From these basic units, you can combine them to arrive at the other units you'll be needing. When an object is moving, or changing its position, you measure that in terms of distance per time, or centimeters per second (cm/s).
On the other hand, when the velocity of an object changes, it is said to accelerate, and the acceleration is measured in terms of the change in speed per time (cm/s/s, or more conventionally, cm/s^2). Earth's gravity acts to accelerate objects at the same rate, an acceleration of 980cm/s^2 often referred to with the symbol g.
A force acts upon a mass to cause it to change speed, or accelerate. Specifically from Newton:
F= m a
Force is measured in units of gram centimeters per second squared (g cm/s^2).
This is a rather cumbersome unit, so you use the units of dynes instead.
Correct Measure
Before going further, it's necessary to correct a long-standing misconception about tracking force. Since tonearm time immemorial, tracking "force" has been described in terms of grams. Unfortunately, grams is a unit of mass, not of force, and the use of units of mass to de scribe force is inappropriate, leading to confusion and incorrect assumptions.
When it is said that an arm has been set up with a "tracking force of 1g," what is really meant is that a force is set equivalent to that of 1g under the influence of gravity. Again, remember that:
F=m a.
The acceleration of gravity is 980cm/s so that 1g exerts a force of:
pivot

FIGURE 1: Single torque source.
So, it is more correct to talk of a tracking force of 980 dynes rather than 1g. Regrettably, the improper use of grams as a measure of tracking force has become all-pervasive and is hard to shake. I would suggest a new unit called the "gram-equivalent of force," which corresponds to the force exerted by 1g under the influence of gravity at the earth's surface, equal to 980 dynes.
Conveniently, though, our choice of units and the planet we live on make the conversion rather easy. One gram equivalent tracking force is within 2% of 1000 dynes, making the conversion pretty easy: 1 gram is about 1000 dynes. The following evaluation shows the tracking force in dynes and gram-equivalent force when convenient.
Dimensional Consistency
One of the primary advantages of using consistent dimensions and units is that it provides a means of verifying that work is proceeding correctly along sound lines.
You can use a method called "dimension al consistency," which verifies that the units and dimensions you start with and the operations you perform on them give you not only the correct numerical results, but the correct units as well.
As an example, a spring and a mass can form a mechanical resonant system.
You are familiar with the formula for the natural frequency of such a system:
F= 1 / 2 ^ pi sqr-rt [M ^x C]
where F is the frequency, M is the mass, and C is the compliance. Well, frequency, mass, and compliance don't tell you much, what you need is frequency, mass, and compliance in units. More specifically, the frequency is in units of Hz (or cycles per second), mass (in this context) in grams, and compliance in centimeters per dyne.
But how, you might ask, does putting mass and compliance together end up in frequency?
Because of the correct use of the proper units, that's how.
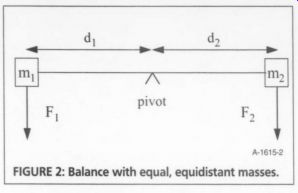
FIGURE 2: Balance with equal, equidistant masses
Looking at this in more detail, you will note that, again, mass is in grams and compliance is in centimeters per dyne. The product of these two, M x C, combines the units and produces a new number in units of gram centimeters per dyne. Well, that seems even more complicated until you re member the definition of a dyne: it's a gram centimeter per second squared. So, in equation form, you simply substitute the definition of a dyne:

------
Now, you can start canceling out units that appear in both the numerator and denominator, since if they appear as factors in both places, the result is one: grams cancel out, centimeters can cel out, and you are left with 1/s2 in the denominator. That's the same as having s2 in the numerator. Take the square root of that and you have simply time, in seconds.
Replace everything that used to be under the radical with a number in units of seconds, and you get:
1 / 2ns
which is in units of "per second." The 2 pi is the number of radians per cycle. Thus, you have started with grams and centimeters per dyne and logically ended with cycles per second, or Hz.
If, instead of mass, you used weight (which, remember, is a force), you'd end up in some weird set of dimensions that do not make logical sense (in this case, the result would be in the reciprocal of the square root of centimeter).
By ensuring dimensional consistency and thus correct units, you can verify that your path is correct and end up with results consistent with the physical system you are dealing with. This article uses dimensional analysis throughout.
Balance In most high-quality tonearms, balance and tracking force is achieved by balancing masses relative to the pivot point.
Gravity exerts forces on each mass of the tonearm, each of these forces producing in turn their own torque around the pivot point (Fig. 1).
Torque (designated as G) is a force around a pivot. The amount of torque is equal to the force times the distance from the pivot:
G=F x d
The force, as mentioned, results from the acceleration of gravity on the mass:
F=mg and g is the acceleration due to gravity, 980cm/s*. As an example, say the mass (m) is 5g, and the distance (d) between that mass and the pivot is 20cm (like a phono cartridge at the end of a tonearm). The force exerted by the mass due to gravity is:
F =5g x 980cm/s? = 4900 dynes and the resulting torque is:
G =4900 dynes x 20cm = 98,000 dyne-cm
In this case, you have a single source of torque, resulting in an unbalanced force, which means that the system will move. To achieve balance, you must have an equal amount of torque, but applied in the opposite direction. One way to do this is to have a mass of equal size an equal distance on the other side of the pivot (Fig. 2).
The total, or net torque on this system then is:
Gypr=Fd, -Fd,
The minus sign in the second term is a result of the torque being applied in the opposite direction.
Since m, = m,, then F, = F,. And since d, = d,, then Fd, = F.d,
If the two terms are equal, then the resulting torque is zero, which is needed to achieve static balance.
Achieving static balance can be done with two equal masses equidistant from the pivot point on opposite sides of the pivot, but that is not the only way. You also achieve static balance when the net sum of all torques around the pivot is zero.
Imagine, instead, a mass of 100g on the right side of the pivot, but only 1 cm from the pivot. Imagine the arrangement for a simple, hypothetical tonearm (Fig. 3).
The force exerted by that counter weight mass is:
Fy = 100g x 980cm/s^2 =
98,000 dynes
Spaced 1cm from the pivot point, it exerts a torque of:
Gy =98,000 dynes x 1 cm = 98,000 dyne-cm.
And the force exerted by that cartridge mass is:
Feu pr = 58 x 980cm/s* = 490 dynes.
Spaced 20cm from the pivot point, it exerts a torque of:

FIGURE 4: Graphing the counterweight distance in relation to pivot. Pivot-counterweight distance
…. precisely equal to the torque exerted by the counterweight on the other side of the pivot.
The sum of these two torques, then, becomes:
Grp = 98,000 dyne-cm - 98,000 dyne-cm =0
The net torque is zero, thus the net forces are zero, and thus the arm is statically balanced.
Applying Tracking Force
To apply tracking force, the arm is usually unbalanced by moving the counterweight.
This results in an unequal application of torque by the cartridge and the counter weight. If the counterweight moves in ward toward the pivot, its contributing torque is reduced, resulting in a total net downwards force at the cartridge.
Looking at this scenario in an analytical fashion, take the previous example, only place the center of mass of the counterweight 0.8cm from the pivot point, rather than 1cm. The torque it now contributes is:
G_cw =98,000 dynes x 0.8cm = 78,400 dyne-cm
The net torque then becomes:
G yer = 98,000 dyne-cm- 78,400 dyne-cm
G_net = 19,600 dyne-cm
Then, at the stylus point, 20cm from the pivot, that unbalanced torque translates into a downward force of:
F_cart = 19,600 dyne-cm + 20cm
F_cart =980 dynes
And 980 dynes is the force equivalent of 1g. By moving the counterweight in a mere 2mm (0.2cm), you've generated 1g equivalent force of tracking weight at the stylus.
Now, with these results, you see that the net forces resulting from unbalanced torque goes as a linear function of the distance of the counterweight (Fig. 4).
This turns out to be very convenient for calibrating the tracking force. Imagine that the tonearm shaft behind the pivot is threaded, and that each turn of the thread is 1 mm apart.
Similarly, the counter-weight is threaded onto this shaft. Rotating the counterweight back and forth on the thread moves the counterweight to wards or away from the pivot. Each turn moves it 1 mm. But a 1 mm change in the position of the tonearm results (in the example) in a change in force of 0.5 gram equivalent (490 dynes).
Now, adjust the counterweight so that the arm is in perfect balance. For a gram force equivalent tracking weight of 1g, simply turn the counterweight on its thread exactly two turns, which moves it 2mm (0.2cm) towards the pivot. How about 1.5g equivalent force? That's three turns. The accuracy of the scheme depends only upon the accuracy of the thread and the weight of the counter weight.
Both of these quantities can be easily designed and controlled during manufacturing to a degree of precision that far exceeds what's necessary in this application. As a result, the tracking-force calibrations on the tonearms that apply tracking force by rotating a counter weight along a thread are usually very accurate, often more so than expensive, often friction-laden tracking-force gauges.
This is contrary to the popular wisdom of the high-end turntable world.
Also see: