Cont. from On The Mechanics of Tonearms, Part 1
In Part 2, the author deals with the concept of moment of inertia in evaluating the effective tonearm mass.
The subject of the effective inertial mass of tonearms is an important one, but it seems to be sorely mis understood, even by alleged "experts." For example, you need only look at some of the claims made in the popular press. One episode in particular stands out: the head of a company making high-quality turntables, in an infamous letter to the editors of Hi-Fi News and Record Review (ca 1976), stated categorically that tonearms cannot have mass; since everything is moving around a pivot, all that mass is really translated into moment of inertia. And without mass, the system can't have a mass-compliance resonance. Unfortunately, the author of this letter failed to persuade tonearms to subscribe to his theory, because they have behaved before and since in every way as if they did have mass.
This confused view of the mechanics of tonearms does, however, serve to highlight that the analysis of the effective mass is not necessarily a straightforward exercise. While not necessarily just simple linear mechanics, it is still well with in the realm of high school physics.
Moment of Inertia
Rotary motion about a pivot point obeys precisely the same physical laws as linear motion, and can be analyzed in the same way. If a body of mass (m) is moving at a velocity (v), its kinetic energy (FE) is:
E=1/2 mv ^2
This is true whether the body is moving in
------ -
Note 1. w (Omega) is usually expressed in radians per second. A radian is the distance around the circumference of the circle equal to the radius of the circle, or, equivalently, the angle at the center of the circle sub tended by an arc equal to the radius. Consequently, there are 2 pi radians in each full circle of revolution.
---------
a straight line or in a uniform circular motion around a pivot point. In the case of circular motion, you can say that the velocity is equal to the product of the angular velocity o! and the distance r from the pivot point:
V=w r
Now, calculating the kinetic energy of such a body merely requires using or in place of v:
E = ½ mv ^2 r^2
Rearranging this equation slightly gives:
a E= So mre :
The quantity mr^2 is called the moment of inertia of the object, and it is an im portant property of all rotating masses It's normally designated by the symbol 7, and, for point objects of mass m that are at a distance r from the center of rotation the moment of inertia is calculated as:
I=mr^2.
Its units are in gram-centimeters squared or gcm^2.

Now, this works fine for point masses (those whose mass is concentrated over a distance that is small compared to 7), but tonearms aren't made of such objects. Just think about the tonearm tube itself, composed of some material with its mass distributed in possibly a complex fashion over the entire distance between the pivot and the cartridge. Some portions are close to the pivot, meaning that r is small; other portions are far away, and r is large. What is the contribution of such an extended object to the total moment of inertia? Well, literally break the problem down and analyze it. Suppose the tonearm tube is a uniform tube 20cm long, weighing, say, 3g. If all its mass were concentrated at the end, far from the pivot, its moment of inertia would be:
I= 3g x (20cm)^2
I= 3g x 400cm^2
I=1200g-cm^2.
On the other hand, if all the mass were concentrated at the pivot point, its moment of inertia would be zero. Halfway along, it would be
I= 3g x (10cm)?
I= 3g x 100cm ^2
I = 300g-cm^2.
The mass, however, is distributed uniformly along the length. Pretend the mass is concentrated into 11 point masses, spaced every 2cm along the arm from the pivot to the end. Point-mass number 1, %1 of a gram, is at the pivot point; point-mass number 11, having the same mass as the first, is at the end. The total moment of inertia is simply the sum of all of the individual point-masses:
I =I +L +.+1,,.
TOTAL
The moment of inertia of mass 1 is:
I, = %ug x (0cm)? = 0g-cm^2, while that of mass 11 is:
I = Yug x (20cm)? = 109g-cm^2.
In fact, you can generalize and say that the moment of inertia of any segment is:
1, =%g x [2(n - 1)em)?, where n equals the segment number, and that the total moment of inertia (in more general terms and standard notation) is:
11 ~ Itotar= X 8 -1)em]?.
n=1

Working this out, the result is 420 g cm^2 You can also divide the length into smaller segments and see what the approximation comes to. With 20 segments, you get 410g-cm^2, with 40, you end up with 405 g-cm^2, and 200 yields 401g-cm^2. And if you carry the experiment far enough, dividing it into, say, 1,000,000 segments, the result is some thing like 400.001g-cm^2.
In fact, consulting a mechanical-engineering handbook, you find that the moment of inertia for a uniform, thin, hollow tube pivoted at one end is:
h mi? 3 I
which agrees with the foregoing approximation to a very high degree. While you're at it, you'll see moment-of-inertia calculations for all sorts of shapes of objects. (I have in front of me a copy of Machinery's Handbook, published by The Industrial Press, that contains a table spanning several pages illustrating the moments of inertia of dozens of different shapes and profiles.) So, for completeness, you would include these calculations into the total. However, for the sake of conciseness, you can confine yourself to the more simple model I describe here.
The Secret of Energy Storage
The implications of all this are significant, in that it tells you that the energy storage is proportional to the mass, but also to the square of the distance of that mass from the center of rotation. One example of the use of this property is the flywheel, as in the simple toy gyroscope, which is de signed to have all its mass concentrated as far from the pivot point as possible, to maximize energy storage.
These implications have important consequences for tonearm design and performance. For instance, an examination of the simple tonearm shows the effects of the placement of masses relative to the pivot. Under the assumption that all portions of the tonearm are rigidly connected together, the cartridge's total moment of inertia is:
Icapr="58 x (20cm)^2 Ic pr="58 4000 Icy pr=2000gcm=, whereas that of the counterweight is:
I = 100g x (1cm)^2 Iy= 100g x lcm^2 I = 100g-cm^2.
with
But hold on a second! The counterweight is 20 times the mass of the cartridge, yet its moment of inertia is 1/20 that of the cartridge. The reason, as you've already seen, is the dependency on the square of the distance from the pivot.
Remember that the total moment is simply the sum of each contributor, so the total is:
Iorar =Tear + ew & Lora = 2000g cm= + 100g-cm Lora; = 2100 g-cm^2.
What is important from this analysis is that for most tonearms, the single largest contributor to the total moment of inertia is the cartridge, not the counterweight.

Now, consider what at first seems to be a completely counterintuitive result. Double the mass of the counterweight to 200g. But, remember, to achieve balance, you must move it closer to the pivot-in this case from 1cm to 0.5cm. Then its contribution to the moment of inertia is:
I = 200g x (0.5cm)^2
I= 200g x 0.25cm^2
I = 50g-cm^2,
and the total now becomes:
Lyoga = 2000 g-cm^2 + 50g-cm^2
Lora = 2050 g-cm^2.
Thus the seemingly contradictory result that making the counterweight heavier reduces the total moment of inertia.
Back to Effective Mass
Well, this moment of inertia seems very interesting, but the goal is to look for the effective mass. How do you convert from total moment of inertia back to the effective mass? The important missing part of the question is, how do you convert back to the effective mass at what point? The obvious answer, I hope, is at the stylus tip, 20cm away from the pivot.
Remember that the moment of inertia for a point mass is:
I=mr2.
Bl 2 )
The objective is to calculate the equivalent mass m at the radius . That's simple (and it's the step that the author of the infamous letter in HFNGRR forgot to take in his incomplete analysis). Simply rearrange the equation so that m is on one side. Divide both sides of the equation by 2 and you get:
A 3 In the example, the arm has a total moment of inertia of 2100g-cm^2, so the resulting effective mass at the stylus tip, 20cm away from the pivot, would be:
2100g - cm^2 EETRoem 2100g - cm^2 Sy ot
See 400cm mpgpp =5.25 grams
And, as you see, the single largest contributor to the total effective mass is the cartridge, not the counterweight. Again, this is a consequence of the dependency on the square of the distance from the pivot.
Now look at the second example, with the 200g counterweight:
2050g -- cm^2 (20cm MEFF =
---------------
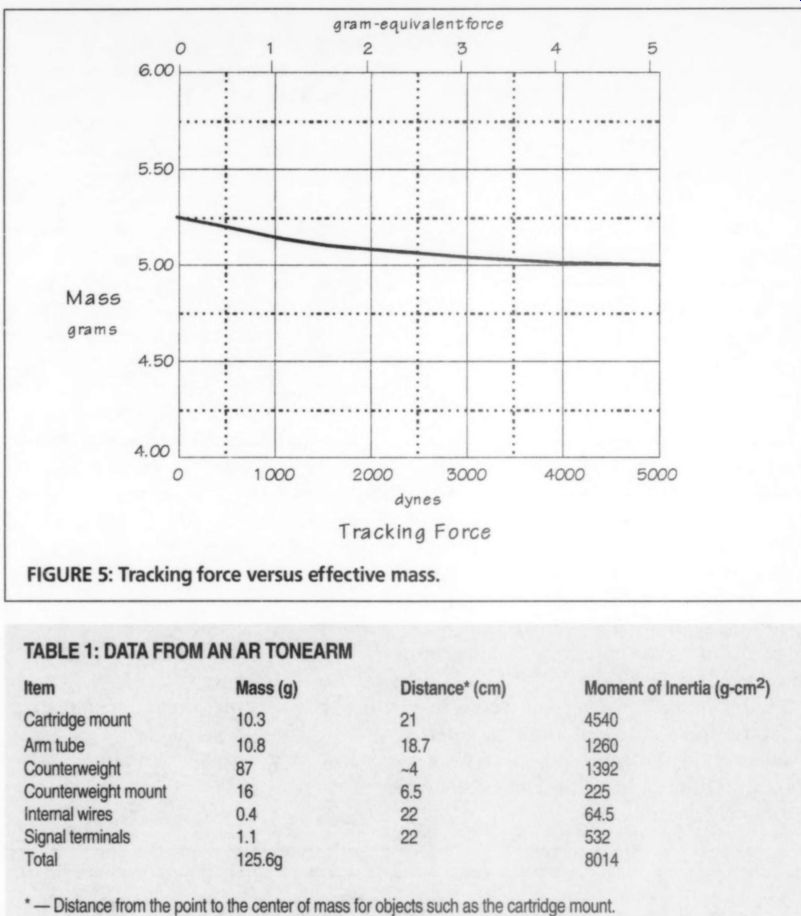
FIGURE 5: Tracking force versus effective mass.
TABLE 1: DATA FROM AN AR TONEARM
item Mass (g) Distance* (cm) Moment of Inertia (g-cm?) Cartridge mount 103 21 4540 Amtbe 108 187 1260 counterweight 87 a 1392 Counter-weight mount 16 65 225 internal wires 04 2 645 Signal terminals 11 2 532 Toul 12569 8014
* - Distance from the point to the center of mass for objects such as the cartridge mount.
----------------
mgpp =5.125 grams.
Again, somewhat counter-intuitively, the arm with the heavier counterweight ended up with the lower effective mass.
Not by a lot, but it's still a real effect.
This, then, contradicts the myth that to lower the mass of a tonearm, all elements must have their mass reduced. It further suggests that if you need to lower the effective mass of an arm, you're much better off spending the effort at the end where the cartridge is, not near the pivot or counterweight.
Tracking Force and Effective Mass
One myth that I have heard repeatedly is that to get the total effective mass, you must add the tracking force to the nor mal effective mass. This would be true if and only if you obtained that tracking force simply by adding a mass right onto the cartridge, sort of like the old trick of taping a penny to the headshell.
Most high-quality tonearms achieve positive tracking force by unbalancing the arm, as discussed previously, moving the counterweight closer to the pivot from the zero-balance position. You can calculate the effects this has on the effective mass.
In the example, it was necessary to move the 100g counterweight to a position 0.8cm away from the pivot point to achieve a 1g equivalent tracking force at the stylus tip. Under that condition, the counterweight's contribution to the total moment of inertia is:
I= 100g x (0.8cm)? Iy= 100g x 0.64cm^2
I = 64g- cm^2
The total moment of inertia becomes Irogar = Icarr + low 4 Lora, = 2000g-cm= + 64g-cm Lops = 2064g-cm^2, and the resulting effective mass, 20cm away from the stylus tip, becomes:
2064g - cm^2 aa]
mgpp =5.16 grams
So, quite contrary to another popular myth, in units that achieve tracking force by unbalancing the tonearm, the tracking force is not added to the effective mass. In fact, dialing in the tracking force by moving the counterweight closer to the pivot from the zero-balance state reduces the effective tonearm mass.
Figure 5, similar to Fig. 4 in Part 1, shows effective mass versus tracking force for the hypothetical tonearm. Here again, you see the counterintuitive effect of the mass decreasing with increasing tracking force, even though the dependence is small, at best. In the example, increasing the tracking force from 1000 to 5000 dynes--an increase of 500%, or a factor of five-results in a reduction of mass of only 3%, a negligible change at the worst.
A More Complete
Model Most of this exploration has been done under the simplifying assumption that the only objects contributing to the effective mass are the cartridge and the counterweight. Clearly, in practical tone arms, there's more than this. At the very minimum, there's also the arm tube, some sort of mounting arrangement for the cartridge, and some kind of support for the counterweight. In addition, you must take into account whatever object at the pivot point holds it all together- although, remember, if it's at the pivot point, its contribution to the effective mass is negligible.
Table 1 contains the actual numbers of effective mass, distance, and moments of inertia derived from a late-model AR tone arm, which is easily disassembled and measured. The stylus-pivot distance of this arm is about 22.5cm, so that the effective mass of the arm, exclusive of the cartridge and its mounting hardware, is:
8014 g - cm^2 =15.8 (22.5cmY oh
This is neither a particularly high-mass nor low-mass tonearm. If you wished to reduce the mass of this arm, there are several approaches. You could increase the mass of the counterweight, moving it closer to the pivot, but that would not accomplish much, since the counter weight contributes only 17% of the total effective mass as it is. The largest gain would be achieved by reducing the amount of mass in the cartridge mounting plate. With some careful shaving, you could remove 5g of material there, which is 5g in effective mass, since it's at the end of the tonearm.
Tonearms with masses approaching 5g or less are rare, often involving some significant compromises in strength and rigidity. Those with masses much greater than 20g limit the range of cartridges you can use to those with low compliances.
Arm Mass and Resonance
The significance of the effective mass in relation to the stylus compliance comes from the fact that together they form a classic mechanical resonant system. It is the combination of the two that deter mines the frequency of that resonance:
1 2n\M pp x C_stylus
where F is the resonant frequency of the system, Mp, is the total effective mass of the arm-cartridge system, and Cg; iS the mechanical compliance of the stylus suspension. As long as you maintain consistency of units, you can simply plug the numbers in, and out comes the resonant frequency in hertz.
The AR example arm combined with a 5g cartridge gives a total effective mass of 21g. Looking at typical moving-magnet compliance, you find compliance figures of 10 x 10~%cm/dynes; that is, for every dyne of force applied to the stylus, it will deflect ten millionths of a centimeter as a result. That means, for example, that if the tracking force is set to 1g equivalent force, or 980 dynes, the stylus deflection will be:
F x=CxF x= 10x 10-S cm/dyne x 980 dynes
x=9.8x 10^3cm, or about 0.1mm.
The resonant frequency of such a system will be:
1 Ferrr-_ 2ny20.8g x 10x 10^5 cm /dyne
Pirillo 2ny 20.8 x 10% gem/gemys 2 ol 1 2x 1.44x 1072s F=11s1, or 11Hz.
The figure of 11Hz is about right for a cartridge/arm resonant frequency, being in the "ideal" range of 7 to 12Hz. If the effective mass of the arm/cartridge were substantially higher, say 42g, the resonant frequency would be lower, less than 8Hz. On the other hand, a cartridge with a very high compliance--say 40 x 10^7 %cm /dyne--would lead to a lower resonance as well-in this case, about 5.5Hz.
The reason the resonance should be within these limits is beyond the scope of this article, but suffice it to say that it is bounded at the top end by the risk of intruding into the musical content of the record, and at the low end by mechanical interference due to external vibrations, mistracking due to warp-induced movements, and so on.
Conclusion
This article has investigated two areas of fundamental mechanics as they apply to tonearm properties: the application of lever arms and torque to determine tracking weight in statically weight-balanced tonearms, and the use of the concept of moment of inertia in evaluating the effective mass of tonearms. You have seen that, especially in the evaluation of effective mass, some of the intuitive assumptions are wrong regarding how each element of the arm contributes to the effective mass. For example, even though it is the most massive object in a tonearm, the counterweight is actually only a minor contributor to the total moving mass. One of the most important concepts to be grasped is that tracking force is not effective mass.
The discussion has covered how the cartridge mass and stylus-suspension compliance interact to form a resonant system, and how that resonance can be calculated. You have also seen that the claim that the tracking force must be added to the effective mass is simply not supportable.
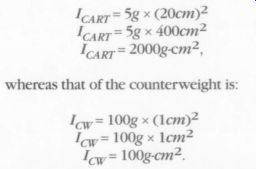
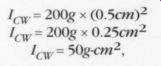





The LP still enjoys a strong and loyal following in some niche markets. While it has clearly dropped out of the main stream of the music-delivery market, there are those who are devoted to its survival. From a practical standpoint, there are still many recordings and significant performances that are simply not available on alternative media (CD, cassette, and so on), meaning that there will, for some time to come, be a need for correct playback of these records. I hope that through this discussion you have acquired a better understanding of those principles underlying record reproduction.
Also see: