1. Introduction
Compression, bit rate reduction and data reduction are all terms which mean basically the same thing in this context. In essence the same (or nearly the same) audio information is carried using a smaller quantity or rate of data. It should be pointed out that in audio, compression traditionally means a process in which the dynamic range of the sound is reduced, typically by broadcasters wishing their station to sound louder.
However, when bit rate reduction is employed, the dynamics of the decoded signal are unchanged. Provided the context is clear, the two meanings can co-exist without a great deal of confusion.
There are several reasons why compression techniques are popular:
(a) Compression extends the playing time of a given storage device.
(b) Compression allows miniaturization. With fewer data to store, the same playing time is obtained with smaller hardware. This is useful in portable and consumer devices.
(c) Tolerances can be relaxed. With fewer data to record, storage density can be reduced, making equipment which is more resistant to adverse environments and which requires less maintenance.
(d) In transmission systems, compression allows a reduction in bandwidth which will generally result in a reduction in cost. This may make possible some process which would be uneconomic without it.
(e) If a given bandwidth is available to an uncompressed signal, compression allows faster than real-time transmission within that bandwidth.
(f) If a given bandwidth is available, compression allows a better-quality signal within that bandwidth.
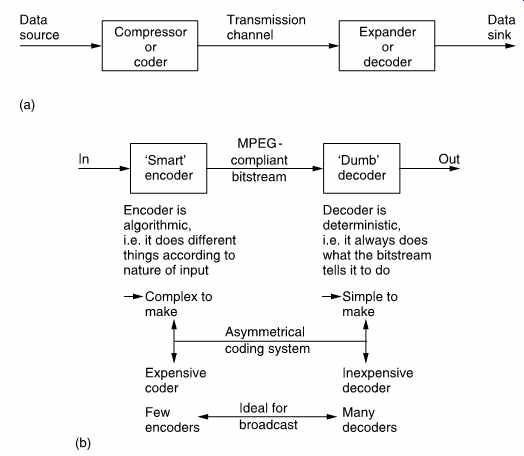
FIG. 1 In (a) a compression system consists of compressor or coder,
a transmission channel and a matching expander or decoder. The combination
of coder and decoder is known as a codec. (b) MPEG is asymmetrical since
the encoder is much more complex than the decoder.
Compression is summarized in FIG. 1. It will be seen in (a) that the PCM audio data rate is reduced at source by the compressor. The compressed data are then passed through a communication channel and returned to the original audio rate by the expander. The ratio between the source data rate and the channel data rate is called the compression factor.
The term coding gain is also used. Sometimes a compressor and expander in series are referred to as a compander. The compressor may equally well be referred to as a coder and the expander a decoder in which case the tandem pair may be called a codec.
Where the encoder is more complex than the decoder the system is said to be asymmetrical. FIG. 1(b) shows that MPEG1,2 audio coders work in this way, as do many others. The encoder needs to be algorithmic or adaptive whereas the decoder is 'dumb' and carries out fixed actions.
This is advantageous in applications such as broadcasting where the number of expensive complex encoders is small but the number of simple inexpensive decoders is large. In point-to-point applications the advantage of asymmetrical coding is not so great. In MPEG audio coding the encoder is typically two or three times as complex as the decoder.
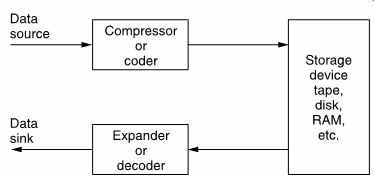
FIG. 2 Compression can be used around a recording medium. The storage
capacity may be increased or the access time reduced according to the application.
FIG. 2 shows the use of a codec with a recorder. The playing time of the medium is extended in proportion to the compression factor. In the case of tapes, the access time is improved because the length of tape needed for a given recording is reduced and so it can be rewound more quickly. In some cases, compression may be used to improve the recorder quality. A lossless coder with a very light compression factor can be used to give a sixteen-bit DAT recorder eighteen- or twenty-bit performance.
In communications, the cost of data links is often roughly proportional to the data rate and so there is simple economic pressure to use a high compression factor. The use of heavy compression to allow audio to be sent over the Internet is an example of this.
In workstations designed for audio editing, the source material is stored on hard disks for rapid access. Whilst top-grade systems may function without compression, many systems use compression to offset the high cost of disk storage.
When a workstation is used for off-line editing, a high compression factor can be used and artifacts will be audible. This is of no consequence as these are only heard by the editor who uses the system to make an EDL (edit decision list) which is no more than a list of actions and the timecodes at which they occur. The original uncompressed material is then conformed to the EDL to obtain a high-quality edited work. When on-line editing is being performed, the output of the workstation is the finished product and clearly a lower compression factor will have to be used.
The cost of digital storage continues to fall and the pressure to use compression for recording purposes falls with it. Perhaps it is in broadcasting and the Internet where the use of compression will have its greatest impact. There is only one electromagnetic spectrum and pressure from other services such as cellular telephones makes efficient use of bandwidth mandatory. Analog broadcasting is an old technology and makes very inefficient use of bandwidth. Its replacement by a compressed digital transmission will be inevitable for the practical reason that the bandwidth is needed elsewhere.
Fortunately in broadcasting there is a mass market for decoders and these can be implemented as low-cost integrated circuits. Fewer encoders are needed and so it is less important if these are expensive. Whilst the cost of digital storage goes down year on year, the cost of electromagnetic spectrum goes up. Consequently in the future the pressure to use compression in recording will ease whereas the pressure to use it in radio communications will increase.
2. Lossless and perceptive coding
Although there are many different audio coding tools, all of them fall into one or other of these categories. In lossless coding, the data from the expander are identical bit-for-bit with the original source data. The so called 'stacker' programs which increase the apparent capacity of disk drives in personal computers use lossless codecs. Clearly with computer programs the corruption of a single bit can be catastrophic. Lossless coding is generally restricted to compression factors of around 2:1.
It is important to appreciate that a lossless coder cannot guarantee a particular compression factor and the communications link or recorder used with it must be able to handle the variable output data rate. Audio material which results in poor compression factors on a given codec is described as difficult. It should be pointed out that the difficulty is often a function of the codec. In other words audio which one codec finds difficult may not be found difficult by another. Lossless codecs can be included in bit-error-rate testing schemes. It is also possible to cascade or concatenate lossless codecs without any special precautions.
In lossy coding, data from the decoder are not identical bit-for-bit with the source data and as a result comparing the input with the output is bound to reveal differences. Clearly lossy codecs are not suitable for computer data, but are used in many audio coders, MPEG included, as they allow greater compression factors than lossless codecs. The most successful lossy codecs are those in which the errors are arranged so that the listener finds them subjectively difficult to detect. Thus lossy codecs must be based on an understanding of psychoacoustic perception and are often called perceptive codes.
Perceptive coding relies on the principle of auditory masking, which was considered in section 2. Masking causes the ear/brain combination to be less sensitive to sound at one frequency in the presence of another at a nearby frequency. If a first tone is present in the input, then it will mask signals of lower level at nearby frequencies. The quantizing of the first tone and of further tones at those frequencies can be made coarser.
Fewer bits are needed and a coding gain results. The increased quantizing distortion is allowable if it is masked by the presence of the first tone.
In perceptive coding, the greater the compression factor required, the more accurately must the human senses be modeled. Perceptive coders can be forced to operate at a fixed compression factor. This is convenient for practical transmission applications where a fixed data rate is easier to handle than a variable rate. However, the result of a fixed compression factor is that the subjective quality can vary with the 'difficulty' of the input material. Perceptive codecs should not be concatenated indiscriminately especially if they use different algorithms. As the reconstructed signal from a perceptive codec is not bit-for-bit accurate, clearly such a codec cannot be included in any bit error rate testing system as the coding differences would be indistinguishable from real errors.
3. Compression principles
In a PCM audio system the bit rate is the product of the sampling rate and the number of bits in each sample and this is generally constant.
Nevertheless the information rate of a real signal varies. In all real signals, part of the signal is obvious from what has gone before or what may come later and a suitable decoder can predict that part so that only the true information actually has to be sent. If the characteristics of a predicting decoder are known, the transmitter can omit parts of the message in the knowledge that the decoder has the ability to recreate it. Thus all encoders must contain a model of the decoder.
In a predictive codec there are two identical predictors, one in the coder and one in the decoder. Their job is to examine a run of previous data values and to extrapolate forward to estimate or predict what the next value will be. This is subtracted from the actual next value at the encoder to produce a prediction error or residual which is transmitted.
The decoder then adds the prediction error to its own prediction to obtain the output code value again. Predictive coding can be applied to any type of information. In audio coders the information may be PCM samples, transform coefficients or even side-chain data such as scale factors.
Predictive coding has the advantage that provided the residual is transmitted intact, there is no loss of information.
One definition of information is that it is the unpredictable or surprising element of data. Newspapers are a good example of information because they only mention items which are surprising.
Newspapers never carry items about individuals who have not been involved in an accident as this is the normal case. Consequently the phrase 'no news is good news' is remarkably true because if an information channel exists but nothing has been sent then it is most likely that nothing remarkable has happened.
The difference between the information rate and the overall bit rate is known as the redundancy. Compression systems are designed to eliminate as much of that redundancy as practicable or perhaps affordable. One way in which this can be done is to exploit statistical predictability in signals. The information content or entropy of a sample is a function of how different it is from the predicted value. Most signals have some degree of predictability. A sine wave is highly predictable, because all cycles look the same. According to Shannon's theory, any signal which is totally predictable carries no information. In the case of the sine wave this is clear because it represents a single frequency and so has no bandwidth.
At the opposite extreme a signal such as noise is completely unpredictable and as a result all codecs find noise difficult. There are two consequences of this characteristic. First, a codec which is designed using the statistics of real material should not be tested with random noise because it is not a representative test. Second, a codec which performs well with clean source material may perform badly with source material containing superimposed noise such as analog tape hiss. Practical compression units may require some form of pre-processing before the compression stage proper and appropriate noise reduction should be incorporated into the pre-processing if noisy signals are anticipated. It will also be necessary to restrict the degree of compression applied to noisy signals.
All real signals fall part-way between the extremes of total predictability and total unpredictability or noisiness. If the bandwidth (set by the sampling rate) and the dynamic range (set by the wordlength) of the transmission system are used to delineate an area, this sets a limit on the information capacity of the system. FIG. 3(a) shows that most real signals only occupy part of that area. The signal may not contain all frequencies, or it may not have full dynamics at certain frequencies.
Entropy can be thought of as a measure of the actual area occupied by the signal. This is the area that must be transmitted if there are to be no subjective differences or artifacts in the received signal. The remaining area is called the redundancy because it adds nothing to the information conveyed. Thus an ideal coder could be imagined which miraculously sorts out the entropy from the redundancy and only sends the former. An ideal decoder would then recreate the original impression of the information quite perfectly.
As the ideal is approached, the coder complexity and the latency (delay) both rise. FIG. 3(b) shows how complexity increases with compression factor. FIG. 3(c) shows how increasing the codec latency can improve the compression factor. Obviously we would have to provide a channel which could accept whatever entropy the coder extracts in order to have transparent quality. As a result moderate coding gains which only remove redundancy need not in principle cause artifacts and can result in systems which are described as subjectively lossless. This assumes that such systems are well engineered, which may not be the case in actual hardware.
If the channel capacity is not sufficient for that, then the coder will have to discard some of the entropy and with it useful information. Larger coding gains which remove some of the entropy must result in artifacts.
It will also be seen from FIG. 3 that an imperfect coder will fail to separate the redundancy and may discard entropy instead, resulting in artifacts at a suboptimal compression factor.

FIG. 3 (a) A perfect coder removes only the redundancy from the input
signal and results in subjectively lossless coding. If the remaining entropy
is beyond the capacity of the channel some of it must be lost and the codec
will then be lossy. An imperfect coder will also be lossy as it fails to
keep all entropy. (b) As the compression factor rises, the complexity must
also rise to maintain quality. (c) High compression factors also tend to
increase latency or delay through the system.
A single variable rate transmission channel is inconvenient and unpopular with channel providers because it is difficult to police. The requirement can be overcome by combining several compressed channels into one constant rate transmission in a way which flexibly allocates data rate between the channels. Provided the material is unrelated, the probability of all channels reaching peak entropy at once is very small and so those channels which are at one instant passing easy material will free up transmission capacity for those channels which are handling difficult material. This is the principle of statistical multiplexing.
Where the same type of source material is used consistently, e.g. English text, then it is possible to perform a statistical analysis on the frequency with which particular letters are used. Variable-length coding is used in which frequently used letters are allocated short codes and letters which occur infrequently are allocated long codes. This results in a lossless code. The well-known Morse code used for telegraphy is an example of this approach. The letter e is the most frequent in English and is sent with a single dot.
An infrequent letter such as z is allocated a long complex pattern. It should be clear that codes of this kind which rely on a prior knowledge of the statistics of the signal are only effective with signals actually having those statistics. If Morse code is used with another language, the transmission becomes significantly less efficient because the statistics are quite different; the letter z, for example, is quite common in Czech.
The Huffman code [3] is one which is designed for use with a data source having known statistics and shares the same principles with the Morse code. The probability of the different code values to be transmitted is studied, and the most frequent codes are arranged to be transmitted with short wordlength symbols. As the probability of a code value falls, it will be allocated longer wordlength. The Huffman code is used in conjunction with a number of compression techniques and is shown in FIG. 4.
The input or source codes are assembled in order of descending probability. The two lowest probabilities are distinguished by a single code bit and their probabilities are combined. The process of combining probabilities is continued until unity is reached and at each stage a bit is used to distinguish the path. The bit will be a zero for the most probable path and one for the least. The compressed output is obtained by reading the bits which describe which path to take going from right to left.
In the case of computer data, there is no control over the data statistics.
Data to be recorded could be instructions, images, tables, text files and so on; each having their own code value distributions. In this case a coder relying on fixed source statistics will be completely inadequate. Instead a system is used which can learn the statistics as it goes along. The Lempel-Ziv-Welch (LZW) lossless codes are in this category. These codes build up a conversion table between frequent long source data strings and short transmitted data codes at both coder and decoder and initially their compression factor is below unity as the contents of the conversion tables are transmitted along with the data. However, once the tables are established, the coding gain more than compensates for the initial loss. In some applications, a continuous analysis of the frequency of code selection is made and if a data string in the table is no longer being used with sufficient frequency it can be deselected and a more common string substituted.
Lossless codes are less common in audio coding where perceptive codes are more popular. The perceptive codes often obtain a coding gain by shortening the wordlength of the data representing the signal waveform.
This must increase the level of quantizing distortion and for good perceived quality the encoder must ensure that the resultant distortion is placed at frequencies where human senses are least able to perceive it. As a result although the received signal is measurably different from the source data, it can appear the same to the human listener under certain conditions.
As these codes rely on the characteristics of human hearing, they can only fully be tested subjectively.
The compression factor of such codes can be set at will by choosing the wordlength of the compressed data. Whilst mild compression may be undetectable, with greater compression factors, artifacts become noticeable.
FIG. 3 shows that this is inevitable from entropy considerations.
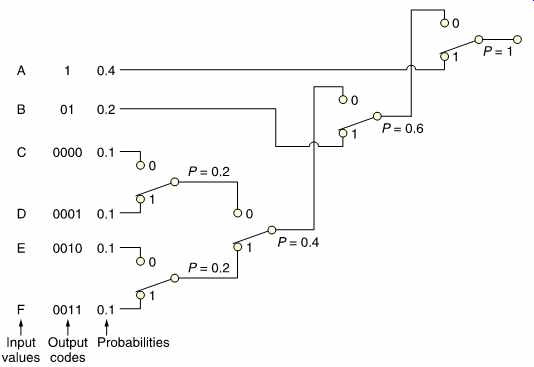
FIG. 4 The Huffman code achieves compression by allocating short codes to frequent
values. To aid deserializing the short codes are not prefixes of longer codes.
4. Codec level calibration
The functioning of the ear is noticeably level dependent and perceptive coders take this into account. However, all signal processing takes place in the electrical or digital domain with respect to electrical or numerical levels whereas the hearing mechanism operates with respect to true sound pressure level. FIG. 5 shows that in an ideal system the overall gain of the microphones and ADCs is such that the PCM codes have a relationship with sound pressure which is the same as that assumed by the model in the codec. Equally the overall gain of the DAC and loudspeaker system should be such that the sound pressure levels which the codec assumes are those actually heard. Clearly the gain control of the microphone and the volume control of the reproduction system must be calibrated if the hearing model is to function properly. If, for example, the microphone gain was too low and this was compensated by advancing the loudspeaker gain, the overall gain would be the same but the codec would be fooled into thinking that the sound pressure level was less than it really was and the masking model would not then be appropriate.
The above should come as no surprise as analog audio codecs such as the various Dolby systems have required and implemented line-up procedures and suitable tones. However obvious the need to calibrate coders may be, the degree to which this is recognized in the industry is almost negligible to date and this can only result in suboptimal performance.
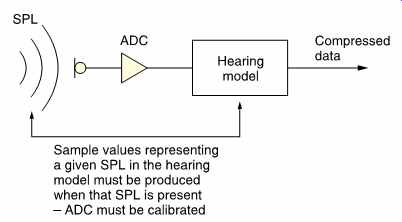
FIG. 5 Audio coders must be level calibrated so that the psychoacoustic
decisions in the coder are based on correct sound pressure levels.
5. Quality measurement
As has been seen, one way in which coding gain is obtained is to requantize sample values to reduce the wordlength. Since the resultant requantizing error is a distortion mechanism it results in energy moving from one frequency to another. The masking model is essential to estimate how audible the effect will be. The greater the degree of compression required, the more precise the model must be. If the masking model is inaccurate, then equipment based upon it may produce audible artifacts under some circumstances. Artifacts may also result if the model is not properly implemented. As a result, development of audio compression units requires careful listening tests with a wide range of source material [4,5] and precision loudspeakers. The presence of artifacts at a given compression factor indicates only that performance is below expectations; it does not distinguish between the implementation and the model. If the implementation is verified, then a more detailed model must be sought. Naturally comparative listening tests are only valid if all the codecs have been level calibrated and if the loudspeakers cause less loss of information than any of the codecs, a requirement which is frequently overlooked.
Properly conducted listening tests are expensive and time consuming, and alternative methods have been developed which can be used objectively to evaluate the performance of different techniques. The noise to masking ratio (NMR) is one such measurement. [6]
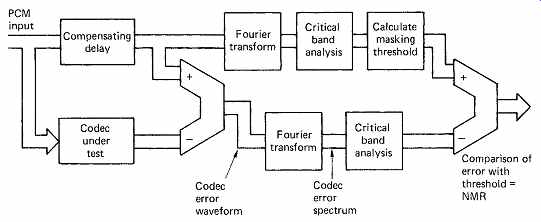
FIG. 6 The noise-to-masking ratio is derived as shown here.
FIG. 6 shows how NMR is measured. Input audio signals are fed simultaneously to a data reduction coder and decoder in tandem and to a compensating delay whose length must be adjusted to match the codec delay. At the output of the delay, the coding error is obtained by subtracting the codec output from the original. The original signal is spectrum-analyzed into critical bands in order to derive the masking threshold of the input audio, and this is compared with the critical band spectrum of the error. The NMR in each critical band is the ratio between the masking threshold and the quantizing error due to the codec. An average NMR for all bands can be computed. A positive NMR in any band indicates that artifacts are potentially audible. Plotting the average NMR against time is a powerful technique, as with an ideal codec the NMR should be stable with different types of program material. If this is not the case the codec could perform quite differently as a function of the source material. NMR excursions can be correlated with the waveform of the audio input to analyze how the extra noise was caused and to redesign the codec to eliminate it.
Practical systems should have a finite NMR in order to give a degree of protection against difficult signals which have not been anticipated and against the use of post-codec equalization or several tandem codecs which could change the masking threshold. There is a strong argument that devices used for audio production should have a greater NMR than consumer or program delivery devices.
6. The limits
There are, of course, limits to all technologies. Eventually artifacts will be heard as the amount of compression is increased which no amount of detailed modeling will remove. The ear is only able to perceive a certain proportion of the information in a given sound. This could be called the perceptual entropy, 7 and all additional sound is redundant or irrelevant.
Compression works by removing the redundancy, and clearly an ideal system would remove all of it, leaving only the entropy. Once this has been done, the masking capacity of the ear has been reached and the NMR has reached zero over the whole band. Assuming an ideal masking model, further reduction of the data rate must cause the level of distortion products to rise above the masking level equally at all frequencies rendering it audible.
The result is that the perceived quality of a codec suddenly falls at a critical bit rate. FIG. 7 shows this effect which is variously known as a crash knee, graceless degradation or the cliff-edge effect. It is a simple consequence of human perception that a coder which keeps to the left of the crash knee 99 per cent of the time will still be marked down because the sudden failure for one per cent of the time causes irritation out of proportion to its duration.
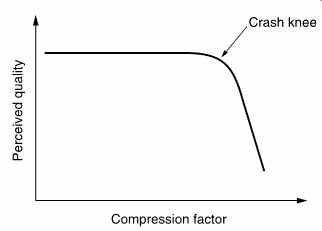
FIG. 7 It is a characteristic of compression systems that failure
is sudden.
In practice the audio bandwidth will have to be reduced in order to keep the distortion level acceptable. For example, in MPEG-1, pre filtering allows data from higher sub-bands to be neglected. MPEG-2 has also introduced some low sampling rate options for this purpose.
Thus there is a limit to the degree of compression which can be achieved even with an ideal coder. Systems which go beyond that limit are not appropriate for high-quality music, but are relevant in news gathering and communications where intelligibility of speech is the criterion.
Interestingly, the data rate out of a coder is virtually independent of the input sampling rate unless the sampling rate is very low. This is because the entropy of the sound is in the waveform, not in the number of samples carrying it.
It follows from the above that to obtain the highest audio quality for a given bit rate, every redundancy in the input signal must be explored.
The more lossless coding tools which can be used, the less will be the extent to which the lossy tools operate. For example, MPEG Layers I and II audio coding don't employ prediction or buffering whereas Layer III uses buffering. MPEG-2 AAC [8] uses both prediction and buffering and can thus obtain better quality at a given bit rate or the same quality at a lower bit rate.
The compression factor of a coder is only part of the story. All codecs cause delay, and in general the greater the compression, the longer the delay. In some applications, such as telephony, a short delay is required. [9] In many applications, the compressed channel will have a constant bit rate, and so a constant compression factor is required. In real program material, the entropy varies and so the NMR will fluctuate. If greater delay can be accepted, as in a recording application, memory buffering can be used to allow the coder to operate at constant NMR and instantaneously variable data rate. The memory absorbs the instantaneous data rate differences of the coder and allows a constant rate in the channel. A higher effective compression factor will then be obtained.
Near-constant quality can also be achieved using statistical multiplexing.
7. Some guidelines
Although compression techniques themselves are complex, there are some simple rules which can be used to avoid disappointment. Used wisely, audio compression has a number of advantages. Used in an inappropriate manner, disappointment is almost inevitable and the technology could get a bad name. The next few points are worth remembering.
_ Compression technology may be exciting, but if it is not necessary it should not be used.
_ If compression is to be used, the degree of compression should be as small as possible; i.e. use the highest practical bit rate.
_ Cascaded compression systems cause loss of quality and the lower the bit rates, the worse this gets. Quality loss increases if any post production steps are performed between compressions.
_ Compression systems cause delay.
_ Compression systems work best with clean source material. Noisy signals give poor results.
_ Compressed data are generally more prone to transmission errors than non-compressed data. The choice of a compression scheme must consider the error characteristics of the channel.
_ Audio codecs need to be level calibrated so that when sound pressure level-dependent decisions are made in the coder those levels actually exist at the microphone.
_ Low bit rate coders should only be used for the final delivery of post produced signals to the end user.
_ Compression quality can only be assessed subjectively on precision loudspeakers. Codecs often sound fine on cheap speakers when in fact they are not.
_ Compression works best in mono and less well in stereo and surround sound systems where the imaging, ambience and reverb are frequently not well reproduced.
_ Don't be browbeaten by the technology. You don't have to understand it to assess the results. Your ears are as good as anyone's so don't be afraid to criticize artifacts.
8. Audio compression tools
There are many different techniques available for audio compression, each having advantages and disadvantages. Real compressors will combine several techniques or tools in various ways to achieve different combinations of cost and complexity. Here it is intended to examine the tools separately before seeing how they are used in actual compression systems.

FIG. 8 Digital companding. In (a) the encoder amplifies the input
to maximum level and the decoder attenuates by the same amount. (b) In
a companded system, the signal is kept as far as possible above the noise
caused by shortening the sample wordlength.
The simplest coding tool is companding which is a digital parallel of the noise reducers used in analog tape recording. FIG. 8(a) shows that in companding the input signal level is monitored. Whenever the input level falls below maximum, it is amplified at the coder. The gain which was applied at the coder is added to the data stream so that the decoder can apply an equal attenuation. The advantage of companding is that the signal is kept as far away from the noise floor as possible. In analog noise reduction this is used to maximize the SNR of a tape recorder, whereas in digital compression it is used to keep the signal level as far as possible above the distortion introduced by various coding steps.
One common way of obtaining coding gain is to shorten the wordlength of samples so that fewer bits need to be transmitted. FIG. 8(b) shows that when this is done, the distortion will rise by 6 dB for every bit removed. This is because removing a bit halves the number of quantizing intervals which then must be twice as large, doubling the error amplitude.
Clearly if this step follows the compander of (a), the audibility of the distortion will be minimized. As an alternative to shortening the wordlength, the uniform quantized PCM signal can be converted to a non-uniform format. In non-uniform coding, shown at (c), the size of the quantizing step rises with the magnitude of the sample so that the distortion level is greater when higher levels exist.
Companding is a relative of floating point coding shown in FIG. 9 where the sample value is expressed as a mantissa and a binary exponent which determines how the mantissa needs to be shifted to have its correct absolute value on a PCM scale. The exponent is the equivalent of the gain setting or scale factor of a compander.
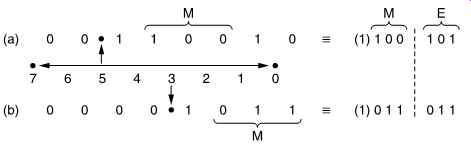
FIG. 9 In this example of floating point notation, the radix point
can have eight positions determined by the exponent E. The point is placed
to the left of the first '1', and the next 4 bits to the right form the
mantissa M. As the MSB of the mantissa is always 1, it need not always
be stored.

FIG. 10 In this example of an eight-bit mantissa, three-bit exponent
system, the maximum SNR is 6 dB x 8 = 48 dB with maximum input of 0 dB.
As input level falls by 6 dB, the convertor noise remains the same, so
SNR falls to 42 dB. Further reduction in signal level causes the convertor
to shift range (point A in the diagram) by increasing the input analog
gain by 6 dB. The SNR is restored, and the exponent changes from 7 to 6
in order to cause the same gain change at the receiver. The noise modulation
would be audible in this simple system. A longer mantissa word is needed
in practice.
Clearly in floating point the signal-to-noise ratio is defined by the number of bits in the mantissa, and as shown in FIG. 10, this will vary as a sawtooth function of signal level, as the best value, obtained when the mantissa is near overflow, is replaced by the worst value when the mantissa overflows and the exponent is incremented. Floating-point notation is used within DSP chips as it eases the computational problems involved in handling long wordlengths. For example, when multiplying floating point numbers, only the mantissae need to be multiplied. The exponents are simply added.
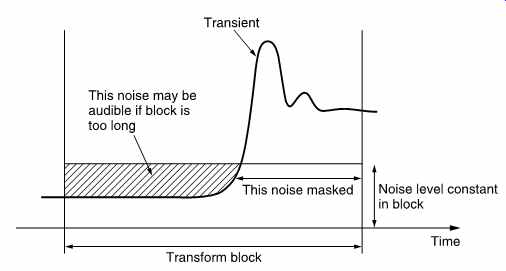
FIG. 11 If a transient occurs towards the end of a transform block,
the quantizing noise will still be present at the beginning of the block
and may result in a pre-echo where the noise is audible before the transient.
A floating point system requires one exponent to be carried with each mantissa and this is wasteful because in real audio material the level does not change so rapidly and there is redundancy in the exponents. A better alternative is floating point block coding, also known as near-instantaneous companding, where the magnitude of the largest sample in a block is used to determine the value of an exponent which is valid for the whole block. Sending one exponent per block requires a lower data rate than in true floating point. [10] In block coding the requantizing in the coder raises the quantizing error, but it does so over the entire duration of the block. FIG. 11 shows that if a transient occurs towards the end of a block, the decoder will reproduce the waveform correctly, but the quantizing noise will start at the beginning of the block and may result in a burst of distortion products (also called pre-noise or pre-echo) which is audible before the transient. Temporal masking may be used to make this inaudible. With a 1ms block, the artifacts are too brief to be heard.
Another solution is to use a variable time window according to the transient content of the audio waveform. When musical transients occur, short blocks are necessary and the coding gain will be low. [11]
At other times the blocks become longer allowing a greater coding gain.
Whilst the above systems used alone do allow coding gain, the compression factor has to be limited because little benefit is obtained from masking. This is because the techniques above produce distortion which may be found anywhere over the entire audio band. If the audio input spectrum is narrow, this noise will not be masked.
Sub-band coding [12] splits the audio spectrum into many different frequency bands. Once this has been done, each band can be individually processed. In real audio signals many bands will contain lower-level signals than the loudest one. Individual companding of each band will be more effective than broadband companding. Sub-band coding also allows the level of distortion products to be raised selectively so that distortion is created only at frequencies where spectral masking will be effective.
It should be noted that the result of reducing the wordlength of samples in a sub-band coder is often referred to as noise. Strictly, noise is an unwanted signal which is decorrelated from the wanted signal. This is not generally what happens in audio compression. Although the original audio conversion would have been correctly dithered, the linearizing random element in the low-order bits will be some way below the end of the shortened word. If the word is simply rounded to the nearest integer the linearizing effect of the original dither will be lost and the result will be quantizing distortion. As the distortion takes place in a bandlimited system the harmonics generated will alias back within the band. Where the requantizing process takes place in a sub-band, the distortion products will be confined to that sub-band as shown in FIG. 12. Such distortion is anharmonic.
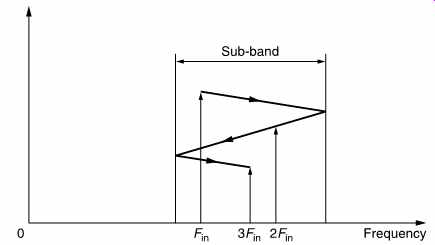
FIG. 12 Requantizing a band-limited signal causes harmonics which
will always alias back within the band.
Following any perceptive coding steps, the resulting data may be further subjected to lossless binary compression tools such as prediction, Huffman coding or a combination of both.
Audio is usually considered to be a time-domain waveform as this is what emerges from a microphone. As has been seen in section 3, spectral analysis allows any periodic waveform to be represented by a set of harmonically related components of suitable amplitude and phase. In theory it is perfectly possible to decompose a periodic input waveform into its constituent frequencies and phases, and to record or transmit the transform. The transform can then be inverted and the original waveform will be precisely recreated.
Although one can think of exceptions, the transform of a typical audio waveform changes relatively slowly much of the time. The slow speech of an organ pipe or a violin string or the slow decay of most musical sounds allow the rate at which the transform is sampled to be reduced, and a coding gain results. At some frequencies the level will be below maximum and a shorter wordlength can be used to describe the coefficient. Further coding gain will be achieved if the coefficients describing frequencies which will experience masking are quantized more coarsely.
In practice there are some difficulties, real sounds are not periodic, but contain transients which transformation cannot accurately locate in time.
The solution to this difficulty is to cut the waveform into short segments and then to transform each individually. The delay is reduced, as is the computational task, but there is a possibility of artifacts arising because of the truncation of the waveform into rectangular time windows. A solution is to use window functions, and to overlap the segments as shown in Figure 13. Thus every input sample appears in just two transforms, but with variable weighting depending upon its position along the time axis.

FIG. 13 Transform coding can only be practically performed on short
blocks. These are overlapped using window functions in order to handle
continuous waveforms.
The DFT (discrete frequency transform) does not produce a continuous spectrum, but instead produces coefficients at discrete frequencies. The frequency resolution (i.e. the number of different frequency coefficients) is equal to the number of samples in the window. If overlapped windows are used, twice as many coefficients are produced as are theoretically necessary. In addition, the DFT requires intensive computation, owing to the requirement to use complex arithmetic to render the phase of the components as well as the amplitude. An alternative is to use discrete cosine transforms (DCT) or the modified discrete cosine transform (MDCT) which has the ability to eliminate the overhead of coefficients due to overlapping the windows and return to the critically sampled domain. [13]
Critical sampling is a term which means that the number of coefficients does not exceed the number which would be obtained with non-overlapping windows.
9. Sub-band coding
Sub-band coding takes advantage of the fact that real sounds do not have uniform spectral energy. The wordlength of PCM audio is based on the dynamic range required and this is generally constant with frequency although any pre-emphasis will affect the situation. When a signal with an uneven spectrum is conveyed by PCM, the whole dynamic range is occupied only by the loudest spectral component, and all the other components are coded with excessive headroom. In its simplest form, sub-band coding works by splitting the audio signal into a number of frequency bands and companding each band according to its own level.
Bands in which there is little energy result in small amplitudes which can be transmitted with short wordlength. Thus each band results in variable length samples, but the sum of all the sample wordlengths is less than that of PCM and so a coding gain can be obtained. Sub-band coding is not restricted to the digital domain; the analog Dolby noise-reduction systems use it extensively.
The number of sub-bands to be used depends upon what other compression tools are to be combined with the sub-band coding. If it is intended to optimize compression based on auditory masking, the sub bands should preferably be narrower than the critical bands of the ear, and therefore a large number will be required. This requirement is frequently not met: ISO/MPEG Layers I and II use only 32 sub-bands.
FIG. 14 shows the critical condition where the masking tone is at the top edge of the sub-band. It will be seen that the narrower the sub-band, the higher the requantizing 'noise' that can be masked. The use of an excessive number of sub-bands will, however, raise complexity and the coding delay, as well as risking pre-ringing on transients which may exceed the temporal masking.
On the other hand, if used in conjunction with predictive sample coding, relatively few bands are required. The apt-X100 system, for example, uses only four sub-bands as simulations showed that a greater number gave diminishing returns. [14]
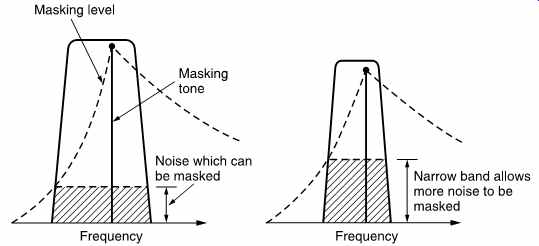
FIG. 14 In sub-band coding the worst case occurs when the masking
tone is at the top edge of the sub-band. The narrower the band, the higher
the noise level which can be masked.
The bandsplitting process is complex and requires a lot of computation.
One bandsplitting method which is useful is quadrature mirror filtering. [15]
The QMF is a kind of twin FIR filter which converts a PCM sample stream into to two sample streams of half the input sampling rate, so that the output data rate equals the input data rate. The frequencies in the lower half of the audio spectrum are carried in one sample stream, and the frequencies in the upper half of the spectrum are carried in the other. Whilst the lower-frequency output is a PCM band-limited representation of the input waveform, the upper frequency output isn't.
A moment's thought will reveal that it could not be so because the sampling rate is not high enough. In fact the upper half of the input spectrum has been heterodyned down to the same frequency band as the lower half by the clever use of aliasing. The waveform is unrecognizable, but when heterodyned back to its correct place in the spectrum in an inverse step, the correct waveform will result once more.
Sampling theory states that the sampling rate needed must be at least twice the bandwidth in the signal to be sampled. If the signal is band limited, the sampling rate need only be more than twice the signal bandwidth not the signal frequency. Downsampled signals of this kind can be reconstructed by a reconstruction or synthesis filter having a bandpass response rather than a low pass response. As only signals within the passband can be output, it is clear from FIG. 15 that the waveform which will result is the original as the intermediate aliased waveform lies outside the passband.

FIG. 15 The sample stream shown would ordinarily represent the waveform
shown in (a), but if it is known that the original signal could exist only
between two frequencies then the waveform in (b) must be the correct one.
A suitable bandpass reconstruction filter, or synthesis filter, will produce
the waveform in (b).
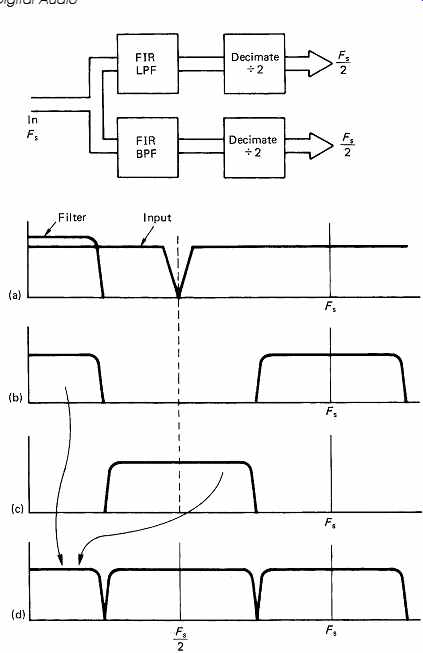
FIG. 16 The quadrature mirror filter. At (a) the input spectrum has
an audio baseband extending up to half the sampling rate. The input is
passed through an FIR low-pass filter which cuts off at one-quarter of
the sampling rate to give the spectrum shown at (b). The input also passes
in parallel through a second FIR filter whose impulse response has been
multiplied by a cosinusoidal waveform in order to amplitude-modulate it.
The resultant impulse gives the filter a mirror image frequency response
shown at (c). The spectra of both (b) and (c) show that both are oversampled
by a factor of two because they are half empty. As a result both can be
decimated by a factor of two, resulting at (d) in two identical Nyquist-sampled
frequency bands of half the original width.
The resultant impulse gives the filter a frequency response shown at (c).
This is a mirror image of the LPF response. If certain criteria are met, the overall frequency response of the two filters is flat. The spectra of both (b) and (c) show that both are oversampled by a factor of 2 because they are half-empty. As a result both can be decimated by a factor of two, which is the equivalent of dropping every other sample. In the case of the lower half of the spectrum, nothing remarkable happens. In the case of the upper half of the spectrum, it has been resampled at half the original frequency as shown at (d). The result is that the upper half of the audio spectrum aliases or heterodynes to the lower half.
An inverse QMF will recombine the bands into the original broadband signal. It is a feature of a QMF/inverse QMF pair that any energy near the band edge which appears in both bands due to inadequate selectivity in the filtering reappears at the correct frequency in the inverse filtering process provided that there is uniform quantizing in all the sub-bands. In practical coders, this criterion is not met, but any residual artifacts are sufficiently small to be masked.
The audio band can be split into as many bands as required by cascading QMFs in a tree. However, each stage can only divide the input spectrum in half. In some coders certain sub-bands will have passed through one splitting stage more than others and will be half their bandwidth. [16]
A delay is required in the wider sub-band data for time alignment.
A simple quadrature mirror is computationally intensive because sample values are calculated which are later decimated or discarded, and an alternative is to use polyphase pseudo-QMF filters17 or wave filters [18] in which the filtering and decimation process is combined. Only wanted sample values are computed. A polyphase QMF operates in a manner not unlike the polyphase operation of a FIR filter used for interpolation in sampling rate conversion (see section 4). In a poly phase filter a set of samples is shifted into position in the transversal register and then these are multiplied by different sets of coefficients and accumulated in each of several phases to give the value of a number of different samples between input samples. In a polyphase QMF, the same approach is used.
FIG. 17 shows an example of a 32-band polyphase QMF having a 512 sample window. With 32 sub-bands, each band will be decimated to 1/32 of the input sampling rate. Thus only one sample in 32 will be retained after the combined filter/decimate operation. The polyphase QMF only computes the value of the sample which is to be retained in each sub band. The filter works in 32 different phases with the same samples in the transversal register. In the first phase, the coefficients will describe the impulse response of a low-pass filter, the so-called prototype filter, and the result of 512 multiplications will be accumulated to give a single
FIG. 16 shows the operation of a simple QMF. At (a) the input spectrum of the PCM audio is shown, having an audio baseband extending up to half the sampling rate and the usual lower sideband extending down from there up to the sampling frequency. The input is passed through a FIR low-pass filter which cuts off at one quarter of the sampling rate to give the spectrum shown at (b). The input also passes in parallel through a second FIR filter which is physically identical, but the coefficients are different. The impulse response of the FIR LPF is multiplied by a cosinusoidal waveform which amplitude modulates it, sample in the first band. In the second phase the coefficients will be obtained by multiplying the impulse response of the prototype filter by a cosinusoid at the centre frequency of the second band. Once more 512 multiply accumulates will be required to obtain a single sample in the second band. This is repeated for each of the 32 bands, and in each case a different centre frequency is obtained by multiplying the prototype impulse by a different modulating frequency. Following 32 such computations, 32 output samples, one in each band, will have been computed. The transversal register then shifts 32 samples and the process repeats.
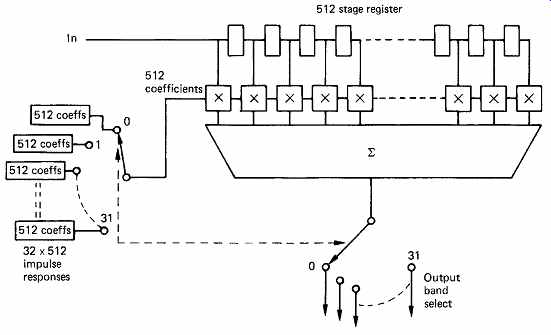
FIG. 17 In polyphase QMF the same input samples are subject to computation
using coefficient sets in many different time-multiplexed phases. The decimation
is combined with the filtering so only wanted values are computed.
The principle of the polyphase QMF is not so different from the techniques used to compute a frequency transform and effectively blurs the distinction between sub-band coding and transform coding.
The QMF technique is restricted to bands of equal width. It might be thought that this is a drawback because the critical bands of the ear are non-uniform. In fact this is only a problem when very high compression factors are required. In all cases it is the masking model of hearing which must have correct critical bands. This model can then be used to determine how much masking and therefore coding gain is possible within the actual sub-bands used. Uniform-width sub-bands will not be able to obtain as much masking as bands which are matched to critical bands, but for many applications the additional coding gain is not worth the added filter complexity.
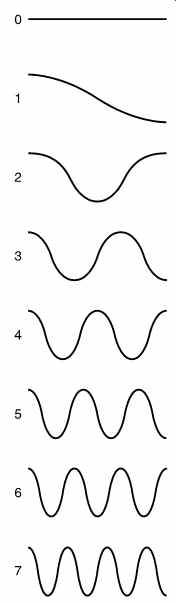
FIG. 18 A table of basis functions for an eight-point DCT. If these
waveforms are added together in various proportions, any original waveform
can be reconstructed. In practice these waveforms are stored as samples,
but after reconstruction to the analog domain they would appear as shown
here.

FIG. 19 An example of an inverse DCT. The coefficients determine the
amplitudes of the waves from the table in FIG. 18 which are to be added
together. Note that coefficient 3 is negative so that the wave is inverted.