The subject of error correction is almost always described in mathematical terms by specialists for the benefit of other specialists. Such mathematical approaches are quite inappropriate for a proper under standing of the concepts of error correction and only become necessary to analyze the quantitative behavior of a system. The description below will use the minimum possible amount of mathematics, and it will then be seen that error correction is, in fact, quite straightforward.
1. Sensitivity of message to error
Before attempting to specify any piece of equipment, it is necessary to quantify the problems to be overcome and how effectively they need to be overcome. For a digital recording system the causes of errors must be studied to quantify the problem, and the sensitivity of the destination to errors must be assessed. In audio the sensitivity to errors must be subjective. In PCM, the effect of a single bit in error depends upon the significance of the bit. If the least significant bit of a sample is wrong, the chances are that the effect will be lost in the noise. Advantage is taken of this in NICAM 728 which does not detect low-order bit errors.
Conversely, if a high-order bit is in error, a massive transient will be added to the sound waveform. The effect of uncorrected errors in PCM audio is rather like that of vehicle ignition interference on a radio.
The effect of errors in delta-modulated data is smaller as every bit has the same significance and the information content of each bit is lower as was explained in Section 4. In some applications, a delta-modulated system can be used without error correction when this would be impossible with PCM.
Whilst the exact BER (bit error rate) which can be tolerated will depend on the application, digital audio is less tolerant of errors than digital video and more tolerant than computer data.
As might be expected, when compression is used, as in DCC, DAB and MiniDisc, much of the redundancy is removed from the data and as a result sensitivity to bit errors inevitably increases. In all these cases, if the maximum error rate which the destination can tolerate is likely to be exceeded by the unaided channel, some form of error handling will be necessary.
There are a number of terms which have idiomatic meanings in error correction. The raw BER is the error rate of the medium, whereas the residual or uncorrected BER is the rate at which the error-correction system fails to detect or mis-corrects errors. In practical digital audio systems, the residual BER is negligibly small. If the error correction is turned off, the two figures become the same.
2. Error mechanisms
There are many different types of recording and transmission channel and consequently there will be many different error mechanisms. In magnetic recording, data can be corrupted by mechanical problems such as media dropout and poor tracking or head contact, or Gaussian thermal noise in replay circuits and heads. In optical recording, contamination of the medium interrupts the light beam. Warped disks and bi-refringent pressings cause de-focusing. Inside equipment, data are conveyed on short wires and the noise environment is under the designer's control.
With suitable design techniques, errors can be made effectively negligible.
In communication systems, there is considerably less control of the electromagnetic environment. In cables, crosstalk and electromagnetic interference occur and can corrupt data, although optical fibers are resistant to interference of this kind. In data networks, errors can be caused if two devices on the same cable inadvertently start transmitting at the same instant.
In long-distance cable transmission the effects of lightning and exchange switching noise must be considered. In DAB, multipath reception causes notches in the received spectrum where signal cancellation takes place. In MOS memories the datum is stored in a tiny charge well which acts as a capacitor (see Section 3) and natural radioactive decay produces alpha particles which have enough energy to discharge a well, resulting in a single bit error. This only happens once every few decades in a single chip, but when large numbers of chips are assembled in computer memories the probability of error rises to once every few minutes. In Section 6 it was seen that when group codes are used, a single defect in a group changes the group symbol and may cause errors up to the size of the group. Single-bit errors are therefore less common in group-coded channels.
Irrespective of the cause, all these mechanisms cause one of two effects.
There are large isolated corruptions, called error bursts, where numerous bits are corrupted all together in an area which is otherwise error-free, and there are random errors affecting single bits or symbols. Whatever the mechanism, the result will be that the received data will not be exactly the same as those sent. It is a tremendous advantage of digital audio that the discrete data bits will each be either right or wrong. A bit cannot be off-colour as it can only be interpreted as 0 or 1. Thus the subtle degradations of analog systems are absent from digital recording and transmission channels and will only be found in convertors. Equally if a binary digit is known to be wrong, it is only necessary to invert its state and then it must be right and indistinguishable from its original value! Thus error correction itself is trivial; the hard part is reliably working out which bits need correcting.
In Section 3 the Gaussian nature of noise probability was discussed.
Some conclusions can be drawn from the Gaussian distribution of noise. [1] First, it is not possible to make error-free digital recordings, because however high the signal-to-noise ratio of the recording, there is still a small but finite chance that the noise can exceed the signal. Measuring the signal-to-noise ratio of a channel establishes the noise power, which determines the width of the noise-distribution curve relative to the signal amplitude. When in a binary system the noise amplitude exceeds the signal amplitude, a bit error will occur. Knowledge of the shape of the Gaussian curve allows the conversion of signal-to-noise ratio into bit error rate (BER). It can be predicted how many bits will fail due to noise in a given recording, but it is not possible to say which bits will be affected.
Increasing the SNR of the channel will not eliminate errors, it just reduces their probability. The logical solution is to incorporate an error-correction system.
3. Basic error correction
Error correction works by adding some bits to the data which are calculated from the data. This creates an entity called a codeword which spans a greater length of time than one bit alone. In recording, the requirement is to spread the codeword over an adequate area of the medium. The statistics of noise means that whilst one bit may be lost in a codeword, the loss of the rest of the codeword because of noise is highly improbable. As will be described later in this section, codewords are designed to be able to correct totally a finite number of corrupted bits.
The greater the timespan or area over which the coding is performed, the greater will be the reliability achieved, although this does mean that greater encoding and decoding delays will have to be accepted.
Shannon [2] proved that a message can be transmitted to any desired degree of accuracy provided that it is spread over a sufficient timespan or area of the medium. Engineers have to compromise, because excessive coding delay is not acceptable. For example, most short digital audio cable interfaces do not employ error correction because the build-up of coding delays in large systems is unacceptable.
If error correction is necessary as a practical matter, it is then only a small step to put it to maximum use. All error correction depends on adding bits to the original message, and this, of course, increases the number of bits to be recorded, although it does not increase the information recorded. It might be imagined that error correction is going to reduce storage or transmission capacity, because space has to be found for all the extra bits. Nothing could be further from the truth. Once an error-correction system is used, the signal-to-noise ratio of the channel can be reduced, because the raised BER of the channel will be overcome by the error-correction system. Reduction of the SNR by 3 dB in a magnetic tape track can be achieved by halving the track width, provided that the system is not dominated by head or preamplifier noise. This doubles the recording density, making the storage of the additional bits needed for error correction a trivial matter. By a similar argument, digital radio transmitters can use less power. In short, error correction is not a nuisance to be tolerated; it is a vital tool needed to maximize the efficiency of recorders. Digital audio would not be economically viable without it.

FIG. 1 The basic stages of an error-correction system. Of these the
most critical is the detection stage, since this controls the subsequent
actions.
4. Error handling
FIG. 1 shows the broad subdivisions of error handling. The first stage might be called error avoidance and includes such measures as creating bad block files on hard disks or using verified media. The data pass through the channel, which causes whatever corruptions it feels like. On receipt of the data the occurrence of errors is first detected, and this process must be extremely reliable, as it does not matter how effective the correction or how good the concealment algorithm if it is not known that they are necessary! The detection of an error then results in a course of action being decided.
A retry is not possible if the data are required in real time for replay purposes. However, in the case of an audio file transfer in a disk-based network, real-time operation is not required. A transmission error due to a network collision or interference will result in a retransmission. If the disk drive detects a read error a retry is easy as the disk is turning at several thousand rpm and will quickly re-present the data. An error due to a dust particle may not occur on the next revolution. Many magnetic tape systems have read after write. During recording, offtape data are immediately checked for errors. If an error is detected, the tape will abort the recording, reverse to the beginning of the current block and erase it.
The data from that block are then recorded further down the tape.
5. Concealment by interpolation
There are some practical differences between data recording for audio and the general computer data-recording application. Although audio recorders seldom have time for retries, they have the advantage that there is a certain amount of redundancy in the information conveyed. In audio systems, if an error cannot be corrected, then it can be concealed. If a sample is lost, it is possible to obtain an approximation to it by interpolating between the samples before and after the missing one.
Clearly concealment of any kind cannot be used with computer data.
In NICAM 728 errors are relatively infrequent and correction is not used. There is simply an error-detecting system which causes samples in error to be concealed. This is described in greater detail in Section 8.
Momentary interpolations are not serious, but sustained use of interpolation can result in aliasing if high frequencies are present in the recording.
In systems which use compression, bit errors are serious because they cause loss of synchronization in variable-length coding, leading to an audible error much larger than the actual data loss. This is known as error-propagation and to avoid it, compressed systems must use reliable error-correction systems. Concealment is also more difficult in compression systems. In advanced concealment systems, a spectral analysis of the sound is made, and if correct sample values are not available, samples having the same spectral characteristics are substituted. This concealment method can conceal greater damage than simple interpolation because the spectral shape changes quite slowly compared to the voltage domain signal.
If there is too much corruption for concealment, the only course in audio is to mute the output as large numbers of uncorrected errors reaching the analog domain cause noise which can be of a high level.
If use is to be made of concealment on replay, the data must generally be reordered or shuffled prior to recording. To take a simple example, odd-numbered samples are recorded in a different area of the medium from even-numbered samples. On playback, if a gross error occurs on the tape, depending on its position, the result will be either corrupted odd samples or corrupted even samples, but it is most unlikely that both will be lost. Interpolation is then possible if the power of the correction system is exceeded.
It should be stressed that corrected data are indistinguishable from the original and thus there can be no audible artifacts. In contrast, concealment is only an approximation to the original information and could be audible. In practical equipment, concealment occurs infrequently unless there is a defect requiring attention.
6. Parity
The error-detection and error-correction processes are closely related and will be dealt with together here. The actual correction of an error is simplified tremendously by the adoption of binary. As there are only two symbols, 0 and 1, it is enough to know that a symbol is wrong, and the correct value is obvious. FIG. 2 shows a minimal circuit required for correction once the bit in error has been identified. The XOR (exclusive OR) gate shows up extensively in error correction and the figure also shows the truth table. One way of remembering the characteristics of this useful device is that there will be an output when the inputs are different.
Inspection of the truth table will show that there is an even number of ones in each row (zero is an even number) and so the device could also be called an even parity gate. The XOR gate is also a adder in modulo 2 (see Section 3).
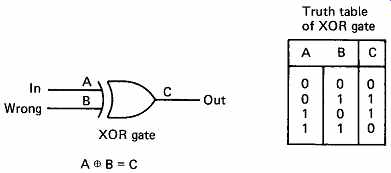
FIG. 2 Once the position of the error is identified, the correction
process in binary is easy.
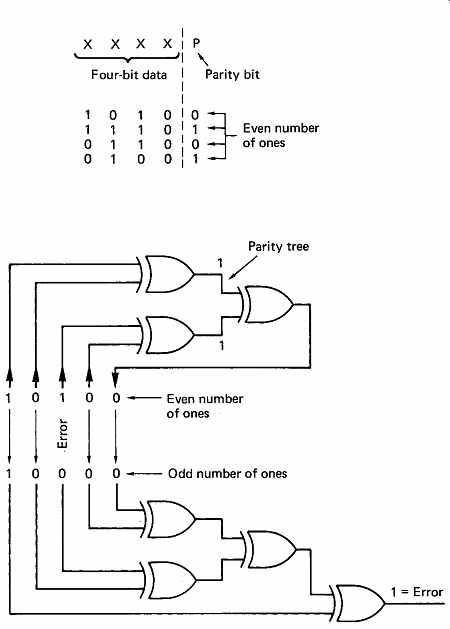
FIG. 3 Parity checking adds up the number of ones in a word using,
in this example, parity trees. One error bit and odd numbers of errors
are detected. Even numbers of errors cannot be detected.
Parity is a fundamental concept in error detection. In FIG. 3, the example is given of a four-bit data word which is to be protected. If an extra bit is added to the word which is calculated in such a way that the total number of ones in the five-bit word is even, this property can be tested on receipt. The generation of the parity bit in FIG. 3 can be performed by a number of the ubiquitous XOR gates configured into what is known as a parity tree. In the figure, if a bit is corrupted, the received message will be seen no longer to have an even number of ones.
If two bits are corrupted, the failure will be undetected. This example can be used to introduce much of the terminology of error correction. The extra bit added to the message carries no information of its own, since it is calculated from the other bits. It is therefore called a redundant bit. The addition of the redundant bit gives the message a special property, i.e. the number of ones is even. A message having some special property irrespective of the actual data content is called a codeword. All error correction relies on adding redundancy to real data to form codewords for transmission. If any corruption occurs, the intention is that the received message will not have the special property; in other words if the received message is not a codeword there has definitely been an error. The receiver can check for the special property without any prior knowledge of the data content. Thus the same check can be made on all received data. If the received message is a codeword, there probably has not been an error.
The word 'probably' must be used because the figure shows that two bits in error will cause the received message to be a codeword, which cannot be discerned from an error-free message. If it is known that generally the only failure mechanism in the channel in question is loss of a single bit, it is assumed that receipt of a codeword means that there has been no error.
If there is a probability of two error bits, that becomes very nearly the probability of failing to detect an error, since all odd numbers of errors will be detected, and a four-bit error is much less likely.
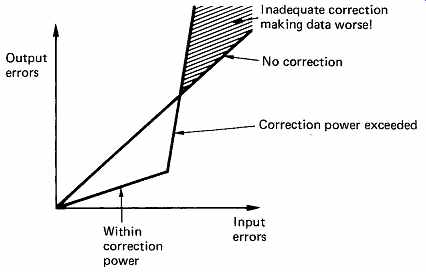
FIG. 4 An error-correction system can only reduce errors at normal
error rates at the expense of increasing errors at higher rates. It is
most important to keep a system working to the left of the knee in the
graph.
It is paramount in all error-correction systems that the protection used should be appropriate for the probability of errors to be encountered. An inadequate error-correction system is actually worse than not having any correction. Error correction works by trading probabilities. Error-free performance with a certain error rate is achieved at the expense of performance at higher error rates. FIG. 4 shows the effect of an error correction system on the residual BER for a given raw BER. It will be seen that there is a characteristic knee in the graph. If the expected raw BER has been misjudged, the consequences can be disastrous. Another result demonstrated by the example is that we can only guarantee to detect the same number of bits in error as there are redundant bits.
7. Block and convolutional codes
FIG. 5(a) shows that in a crossword, or product, code the data are formed into a two-dimensional array, in which each location can be a single bit or a multi-bit symbol. Parity is then generated on both rows and columns. If a single bit or symbol fails, one row parity check and one column parity check will fail, and the failure can be located at the intersection of the two failing checks. Although two symbols in error confuse this simple scheme, using more complex coding in a two dimensional structure is very powerful, and further examples will be given throughout this section.
The example of FIG. 5(a) assembles the data to be coded into a block of finite size and then each codeword is calculated by taking different set of symbols. This should be contrasted with the operation of the circuit of FIG. 5(b). Here the data are not in a block, but form an endless stream. A shift register allows four symbols to be available simultaneously to the encoder. The action of the encoder depends upon the delays. When symbol 3 emerges from the first delay, it will be added (modulo 2) to symbol 6. When this sum emerges from the second delay, it will be added to symbol 9 and so on. The codeword produced is shown in FIG. 5(c) where it will be seen to be bent such that it has a vertical section and a diagonal section. Four symbols later the next codeword will be created one column further over in the data.
This is a convolutional code because the coder always takes parity on the same pattern of symbols which is convolved with the data stream on an endless basis. FIG. 5(c) also shows that if an error occurs, it will cause a parity error in two codewords. The error will be on the diagonal part of one codeword and on the vertical part of the other so that it can uniquely be located at the intersection and corrected by parity.
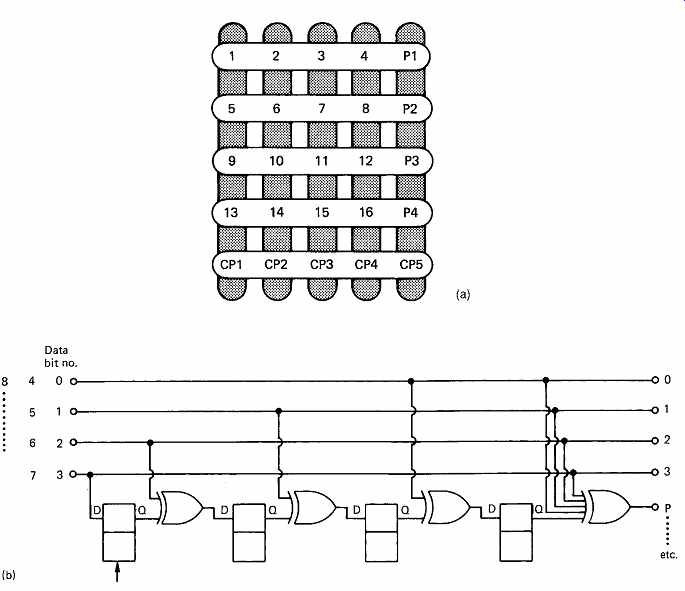
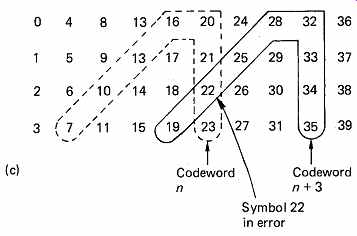
FIG. 5 A block code is shown in (a). Each location in the block can
be a bit or a word. Horizontal parity checks are made by adding P1, P2,
etc., and cross-parity or vertical checks are made by adding CP1, CP2,
etc.
Any symbol in error will be at the intersection of the two failing codewords. In (b) a convolutional coder is shown. Symbols entering are subject to different delays which result in the codewords in (c) being calculated.
These have a vertical part and a diagonal part. A symbol in error will be at the intersection of the diagonal part of one code and the vertical part of another.
Comparison with the block code of FIG. 5(a) will show that the convolutional code needs less redundancy for the same single-symbol location and correction performance as only a single redundant symbol is required for every four data symbols. Convolutional codes are computed on an endless basis which makes them inconvenient in recording applications where editing is anticipated. Here the block code is more appropriate as it allows edit gaps to be created between codes. In the case of uncorrectable errors, the convolutional principle causes the syndromes to be affected for some time afterwards and results in mis-corrections of symbols which were not actually in error.
This is a further example of error propagation and is a characteristic of convolutional codes. Recording media tend to produce somewhat variant error statistics because media defects and mechanical problems cause errors which do not fit the classical additive noise channel.
Convolutional codes can easily be taken beyond their correcting power if used with real recording media.
In transmission and broadcasting, the error statistics are more stable and the editing requirement is absent. As a result, convolutional codes are used in DAB and DVB whereas block codes are used in recording.
Convolutional codes are not restricted to the simple parity example given here, but can be used in conjunction with more sophisticated redundancy techniques such as the Reed-Solomon codes.
8. Hamming code
In a one-dimensional code, the position of the failing bit can be determined by using more parity checks. In FIG. 6, the four data bits have been used to compute three redundancy bits, making a seven-bit codeword. The four data bits are examined in turn, and each bit which is a one will cause the corresponding row of a generator matrix to be added to an exclusive-OR sum. For example, if the data were 1001, the top and bottom rows of the matrix would be XORed. The matrix used is known as an identity matrix, because the data bits in the codeword are identical to the data bits to be conveyed. This is useful because the original data can be stored unmodified, and the check bits are simply attached to the end to make a so-called systematic codeword. Almost all digital recording equipment uses systematic codes. The way in which the redundancy bits are calculated is simply that they do not all use every data bit. If a data bit has not been included in a parity check, it can fail without affecting the outcome of that check. The position of the error is deduced from the pattern of successful and unsuccessful checks in the check matrix. This pattern is known as a syndrome.
In the figure the example of a failing bit is given. Bit three fails, and because this bit is included in only two of the checks, there are two ones in the failure pattern, 011. As some care was taken in designing the matrix pattern for the generation of the check bits, the syndrome, 011, is the address of the failing bit. This is the fundamental feature of the Hamming codes due to Richard Hamming. [3]
The performance of this seven-bit codeword can be assessed. In seven bits there can be 128 combinations, but in four data bits there are only sixteen combinations. Thus out of 128 possible received messages, only sixteen will be codewords, so if the message is completely trashed by a gross corruption, it will still be possible to detect that this has happened 112 times out of 127, as in these cases the syndrome will be non-zero (the 128th case is the correct data).
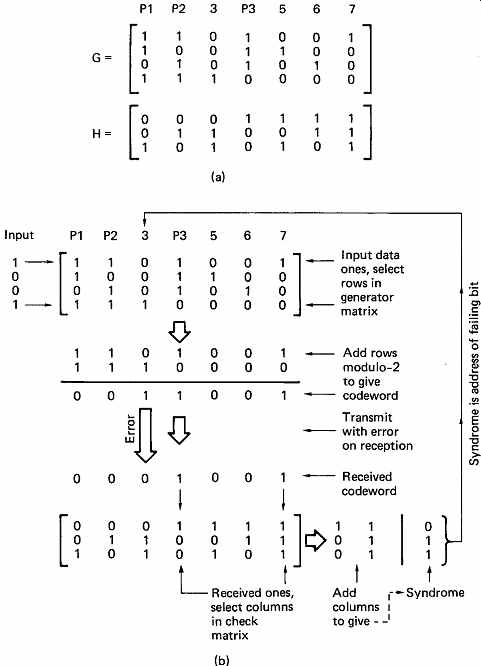
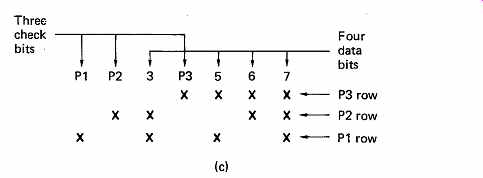
FIG. 6 (a) The generator and check matrices of a Hamming code. The
data and check bits are arranged as shown because this causes the syndrome
to be the binary address of the failing bit. (b) An example of Hamming-code
generation and error correction. (c) Another way of looking at Hamming
code is to say that the rows of crosses in this chart are calculated to
have even parity. If bit 3 fails, parity check P3 is not affected, but
parity checks P1 and P2 both include bit 3 and will fail.
There is thus only a probability of detecting that all of the message is corrupt. In an idle moment it is possible to work out, in a similar way, the number of false codewords which can result from different numbers of bits being assumed to have failed. For fewer than three bits, the failure will always be detected, because there are three check bits. Returning to the example, if two bits fail, there will be a non-zero syndrome, but if this is used to point to a bit in error, a miscorrection will result. From these results can be deduced another important feature of error codes. The power of detection is always greater than the power of correction, which is also fortunate, since if the correcting power is exceeded by an error it will at least be a known problem, and steps can be taken to prevent any undesirable consequences.
The efficiency of the example given is not very high because three check bits are needed for every four data bits. Since the failing bit is located with a binary-split mechanism, it is possible to double the code length by adding a single extra check bit. Thus with four-bit syndromes there are fifteen non-zero codes and so the codeword will be fifteen bits long. Four bits are redundant and eleven are data. Using five bits of redundancy, the code can be 31 bits long and contain 26 data bits. Thus provided that the number of errors to be detected stays the same, it is more efficient to use long codewords. Error-correcting memories use typically four or eight data bytes plus redundancy. A drawback of long codes is that if it is desired to change a single memory byte it is necessary to read the entire codeword, modify the desired data byte and re-encode, the so-called read-modify-write process.
The Hamming code shown is limited to single-bit correction, but by addition of another bit of redundancy can be made to correct one-bit and detect two-bit errors. This is ideal for error-correcting MOS memories where the SECDED (single-error correcting double-error detecting) characteristic matches the type of failures experienced.
The correction of one bit is of little use in the presence of burst errors, but a Hamming code can be made to correct burst errors by using interleaving.
FIG. 7 shows that if several codewords are calculated beforehand and woven together as shown before they are sent down the channel, then a burst of errors which corrupts several bits will become a number of single bit errors in separate codewords upon de-interleaving.
Interleaving is used extensively in digital recording and transmission, and will be discussed in greater detail later in this section.

FIG. 7 The vertical columns of this diagram are all codewords generated
by the matrix of FIG. 6, which can correct a single-bit error. If these
words are recorded in the order shown, a burst error of up to four bits
will result in one single-bit error in each codeword, which is correctable.
Interleave requires memory, and causes delay.
De-interleave requires the same.
9. Hamming distance
It is useful at this point to introduce the concept of Hamming distance. It is not a physical distance but is a specific measure of the difference between two binary numbers. Hamming distance is defined in the general case as the number of bit positions in which a pair of words differ.
The Hamming distance of a code is defined as the minimum number of bits that must be changed in any codeword in order to turn it into another codeword. This is an important yardstick because if errors convert one codeword into another, it will have the special characteristic of the code and so the corruption will not even be detected.
FIG. 8 shows Hamming distance diagrammatically. A three-bit codeword is used with two data bits and one parity bit. With three bits, a received code could have eight combinations, but only four of these will be codewords. The valid codewords are shown in the center of each of the disks, and these will be seen to be identical to the rows of the truth table in FIG. 2. At the perimeter of the disks are shown the received words which would result from a single-bit error, i.e. they have a Hamming distance of one from codewords. It will be seen that the same received word (on the vertical bars) can be obtained from a different single-bit corruption of any three codewords. It is thus not possible to tell which codeword was corrupted, so although all single-bit errors can be detected, correction is not possible. This diagram should be compared with that of FIG. 9, which is a Venn diagram where there is a set in which the MSB is 1 (upper circle), a set in which the middle bit is 1 (lower left circle) and a set in which the LSB is 1 (lower right circle). Note that in crossing any boundary only one bit changes, and so each boundary represents a Hamming distance change of one. The four codewords of FIG. 8 are repeated here, and it will be seen that single-bit errors in any codeword produce a non-codeword, and so single-bit errors are always detectable.
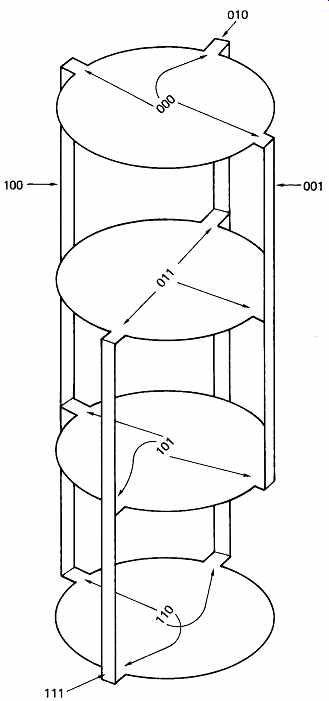
FIG. 8 Hamming distance of two. The disk centers contain codewords.
Corrupting each bit in turn produces the distance 1 values on the vertical
members. In order to change one codeword to another, two bits must be changed,
so the code has a Hamming distance of two.

FIG. 9 Venn diagram shows a one-bit change crossing any boundary which
is a Hamming distance of one. Compare with FIG. 8. Codewords marked*.
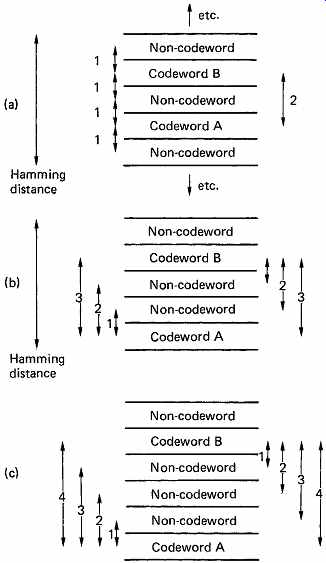
FIG. 10 (a) Distance 2 code; non-codewords are at distance 1 from
two possible codewords so it cannot be deduced what the correct one is.
(b) Distance 3 code; non-codewords which have single-bit errors can be
attributed to the nearest codeword. Breaks down in presence of double-bit
errors. (c) Distance 4 code; non-codewords which have single-bit errors can
be attributed to the nearest codeword, AND double-bit errors form different
non-codewords, and can thus be detected but not corrected.
Correction is possible if the number of non-codewords is increased by increasing the number of redundant bits. This means that it is possible to spread out the actual codewords in Hamming distance terms.
FIG. 10(a) shows a distance 2 code, where there is only one redundancy bit, and so half of the possible words will be codewords.
There will be non-codewords at distance 1 which can be produced by altering a single bit in either of two codewords. In this case it is not possible to tell what the original codeword was in the case of a single-bit error.
FIG. 10(b) shows a distance 3 code, where there will now be at least two non-codewords between codewords. If a single-bit error occurs in a codeword, the resulting non-codeword will be at distance 1 from the original codeword. This same non-codeword could also have been produced by changing two bits in a different codeword. If it is known that the failure mechanism is a single bit, it can be assumed that the original codeword was the one which is closest in Hamming distance to the received bit pattern, and so correction is possible. If, however, our assumption about the error mechanism proved to be wrong, and in fact a two-bit error had occurred, this assumption would take us to the wrong codeword, turning the event into a three-bit error. This is an illustration of the knee in the graph of FIG. 4, where if the power of the code is exceeded it makes things worse.
FIG. 10(c) shows a distance 4 code. There are now three non codewords between codewords, and clearly single-bit errors can still be corrected by choosing the nearest codeword. Double-bit errors will be detected, because they result in non-codewords equidistant in Hamming terms from codewords, but it is not possible to determine what the original codeword was.
10. Cyclic codes
The parallel implementation of a Hamming code can be made very fast using parity trees, which is ideal for memory applications where access time is increased by the correction process. However, in digital audio recording applications, the data are stored serially on a track, and it is desirable to use relatively large data blocks to reduce the amount of the medium devoted to preambles, addressing and synchronizing. Where large data blocks are to be handled, the use of a look-up table or tree has to be abandoned because it would become impossibly large. The principle of codewords having a special characteristic will still be employed, but they will be generated and checked algorithmically by equations. The syndrome will then be converted to the bit(s) in error not by looking them up, but by solving an equation.

FIG. 11 When seven successive bits A-G are clocked into this circuit,
the contents of the three latches are shown for each clock. The final result
is a parity-check matrix.
Where data can be accessed serially, simpler circuitry can be used because the same gate will be used for many XOR operations.
Unfortunately the reduction in component count is only paralleled by an increase in the difficulty of explaining what takes place.
The circuit of FIG. 11 is a kind of shift register, but with a particular feedback arrangement which leads it to be known as a twisted-ring counter. If seven message bits A-G are applied serially to this circuit, and each one of them is clocked, the outcome can be followed in the diagram.
As bit A is presented and the system is clocked, bit A will enter the left hand latch. When bits B and C are presented, A moves across to the right.
Both XOR gates will have A on the upper input from the right-hand latch, the left one has D on the lower input and the right one has B on the lower input. When clocked, the left latch will thus be loaded with the XOR of A and D, and the right one with the XOR of A and B. The remainder of the sequence can be followed, bearing in mind that when the same term appears on both inputs of an XOR gate, it goes out, as the exclusive-OR of something with itself is nothing. At the end of the process, the latches contain three different expressions. Essentially, the circuit makes three parity checks through the message, leaving the result of each in the three stages of the register. In the figure, these expressions have been used to draw up a check matrix. The significance of these steps can now be explained.
The bits A B C and D are four data bits, and the bits E F and G are redundancy. When the redundancy is calculated, bit E is chosen so that there are an even number of ones in bits A B C and E; bit F is chosen such that the same applies to bits B C D and F, and similarly for bit G. Thus the four data bits and the three check bits form a seven-bit codeword. If there is no error in the codeword, when it is fed into the circuit shown, the result of each of the three parity checks will be zero and every stage of the shift register will be cleared. As the register has eight possible states, and one of them is the error-free condition, then there are seven remaining states, hence the seven-bit codeword. If a bit in the codeword is corrupted, there will be a non-zero result. For example, if bit D fails, the check on bits A B D and G will fail, and a one will appear in the left-hand latch. The check on bits B C D F will also fail, and the center latch will set. The check on bits A B C E will not fail, because D is not involved in it, making the right-hand bit zero. There will be a syndrome of 110 in the register, and this will be seen from the check matrix to correspond to an error in bit D. Whichever bit fails, there will be a different three-bit syndrome which uniquely identifies the failed bit. As there are only three latches, there can be eight different syndromes. One of these is zero, which is the error-free condition, and so there are seven remaining error syndromes. The length of the codeword cannot exceed seven bits, or there would not be enough syndromes to correct all the bits. This can also be made to tie in with the generation of the check matrix. If fourteen bits, A to N, were fed into the circuit shown, the result would be that the check matrix repeated twice, and if a syndrome of 101 were to result, it could not be determined whether bit D or bit K failed.
Because the check repeats every seven bits, the code is said to be a cyclic redundancy check (CRC) code.
In FIG. 6 an example of a Hamming code was given. Comparison of the check matrix of FIG. 11 with that of FIG. 6 will show that the only difference is the order of the matrix columns. The two different processes have thus achieved exactly the same results, and the performance of both must be identical. This is not true in general, but a very small cyclic code has been used for simplicity and to allow parallels to be seen.
In practice CRC code blocks will be much longer than the blocks used in Hamming codes.
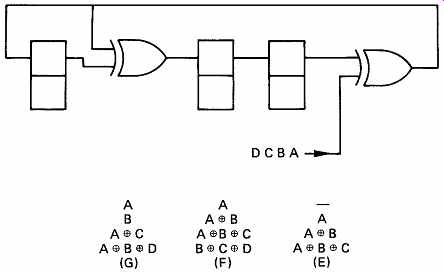
FIG. 12 By moving the insertion point three places to the right, the
calculation of the check bits is completed in only four clock periods and
they can follow the data immediately. This is equivalent to pre-multiplying
the data by x^3
It has been seen that the circuit shown makes a matrix check on a received word to determine if there has been an error, but the same circuit expressed as a list of powers of two. For example, the binary number 1101 means 8 + 4 + 1, and can be written:
23 + 22 + 20
In fact, much of the theory of error correction applies to symbols in number bases other than 2, so that the number can also be written more generally as
X^3 + x^2 + 1 (20 =1)
which also looks much more impressive. This expression, containing as it does various powers, is of course a polynomial, and the circuit of FIG. 11 which has been seen to construct a parity-check matrix on a codeword can also be described as calculating the remainder due to dividing the input by a polynomial using modulo-2 arithmetic. In modulo-2 there are no borrows or carries, and addition and subtraction are replaced by the XOR function, which makes hardware implementation very easy. In FIG. 13 it will be seen that the circuit of FIG. 11 actually divides the codeword by a polynomial which is:
x^3 + x + 1 or 1011
This can be deduced from the fact that the right-hand bit is fed into two lower-order stages of the register at once. Once all the bits of the message have been clocked in, the circuit contains the remainder. In mathematical terms, the special property of a codeword is that it is a polynomial which yields a remainder of zero when divided by the generating polynomial.
The receiver will make this division, and the result should be zero in the error-free case. Thus the codeword itself disappears from the division. If an error has occurred it is considered that this is due to an error polynomial which has been added to the codeword polynomial. If a codeword divided by the check polynomial is zero, a non-zero syndrome must represent the error polynomial divided by the check polynomial.
Thus if the syndrome is multiplied by the check polynomial, the latter will be cancelled out and the result will be the error polynomial. If this is added modulo-2 to the received word, it will cancel out the error and leave the corrected data.
Some examples of modulo-2 division are given in FIG. 13 which can be compared with the parallel computation of parity checks according to the matrix of FIG. 11.
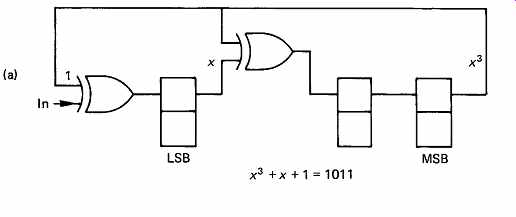
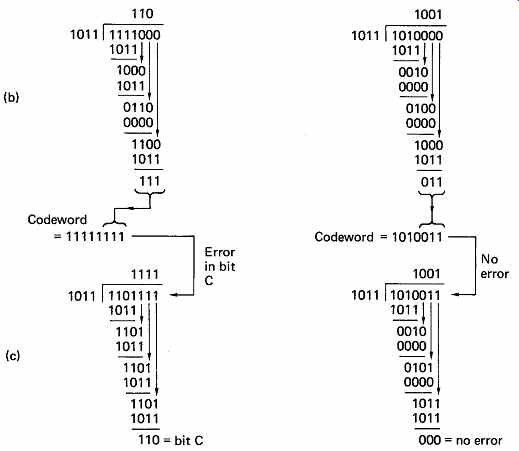
FIG. 13 (a) Circuit of FIG. 11 divides by x^3 + x + 1 to find
remainder. At (b) this is used to calculate check bits. At (c) right, zero
syndrome, no error.
The process of generating the codeword from the original data can also be described mathematically. If a codeword has to give zero remainder when divided, it follows that the data can be converted to a codeword by adding the remainder when the data are divided.
Generally speaking, the remainder would have to be subtracted, but in modulo-2 there is no distinction. This process is also illustrated in FIG. 13. The four data bits have three zeros placed on the right hand end, to make the wordlength equal to that of a codeword, and this word is then divided by the polynomial to calculate the remainder.
The remainder is added to the zero-extended data to form a codeword.
The modified circuit of FIG. 12 can be described as premultiplying the data by x^3 before dividing.
CRC codes are of primary importance for detecting errors, and several have been standardized for use in digital communications. The most common of these are:
x^16 + x^15 + x^2 + 1 (CRC-16) x^16 + x^12 + x^5 + 1 (CRC-CCITT)
The implementation of the cyclic codes is much easier if all the necessary logic is present in one integrated circuit. The Fairchild 9401 was found in early digital audio equipment because it implemented a variety of polynomials including the two above. A feature of the chip is that the feedback register can be configured to work backwards if required. The desired polynomial is selected by a three-bit control code as shown in FIG. 14. The code is implemented by switching in a particular feedback configuration stored in ROM. During recording or transmission, the serial data are clocked in whilst the control input CWE (check word enable) is held true. At the end of the serial data, this input is made false and this has the effect of disabling the feedback so that the device becomes a conventional shift register and the CRCC is clocked out of the Q output and appended to the data. On playback, the entire message is clocked into the device with CWE once more true. At the end, if the register contains all zeros, the message was a codeword. If not, there has been an error.
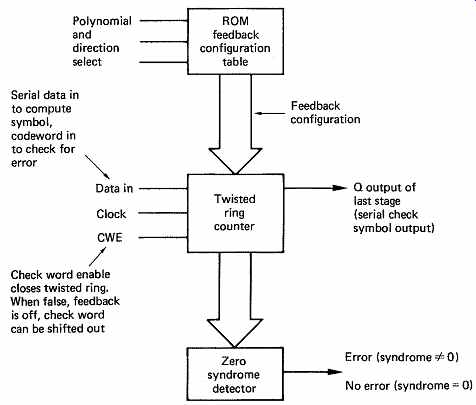
FIG. 14 Simplified block of CRC chip which can implement several polynomials,
and both generate and check redundancy.
11. Punctured codes

FIG. 15 Codewords are often shortened, or punctured, which means that
only the end of the codeword is actually transmitted. The only precaution
to be taken when puncturing codes is that the computed position of an error
will be from the beginning of the codeword, not from the beginning of the
message.
The sixteen-bit cyclic codes have codewords of length 2^16- 1 or 65,535 bits long. This may be too long for the application. Another problem with very long codes is that with a given raw BER, the longer the code, the more errors will occur in it. There may be enough errors to exceed the power of the code. The solution in both cases is to shorten or puncture the code. FIG. 15 shows that in a punctured code, only the end of the codeword is used, and the data and redundancy are preceded by a string of zeros. It is not necessary to record these zeros, and, of course, errors cannot occur in them. Implementing a punctured code is easy. If a CRC generator starts with the register cleared and is fed with serial zeros, it will not change its state. Thus it is not necessary to provide the zeros, and encoding can begin with the first data bit. In the same way, the leading zeros need not be provided during playback. The only precaution needed is that if a syndrome calculates the location of an error, this will be from the beginning of the codeword not from the beginning of the data. Where codes are used for detection only, this is of no consequence.
12. Applications of cyclic codes
FIG. 16 The CRCC in the AES/EBU interface is generated by premultiplying the data by x^8 and dividing by x^8 + x^4 + x^3 + x^2 + 1. The process can be performed on a serial input by the circuit shown. Premultiplication is achieved by connecting the input at the most significant end of the system. If the output of the right-hand XOR gate is 1 then a 1 is fed back to all of the powers shown, and the polynomial process required is performed. At the end of 23 data bytes, the CRCC will be in the eight latches. At the end of an error-free 24 byte message, the latches will be all zero.
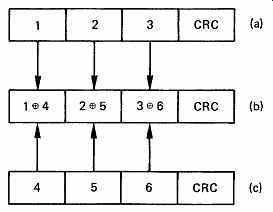
FIG. 17 The simple crossword code of the PCM-1610/1630 format. Horizontal
codewords are cyclic polynomials; vertical codewords are simple parity.
Cyclic code detects errors and acts as erasure pointer for parity correction.
For example, if word 2 fails, CRC (a) fails, and 1, 2 and 3 are all erased.
The correct values are computed from (b) and (c) such that:
1 = (1 _ 4) _ 4 2 = (2 _ 5) _ 5 3 = (3 _ 6) _ 6
The AES/EBU digital audio interface described in Section 8 uses an eight-bit cyclic code to protect the channel-status data. The polynomial used and a typical circuit for generating it can be seen in FIG. 16. The full codeword length is 255 bits but it is punctured to 192 bits, or 24 bytes which is the length of the AES/EBU channel status block. The CRCC is placed in the last byte.
The Sony PCM-1610/1630 CD mastering recorders used a sixteen-bit cyclic code for error detection. FIG. 17 shows that in this system, two sets of three sixteen-bit audio samples have a CRCC added to form punctured codewords 64 bits long. The PCM-1610 used the 9401 chip of FIG. 14 to perform the calculation. Three parity words are formed by taking the XOR of the two sets of samples and a CRCC is added to this also.
The three codewords are then recorded. If an error should occur, one of the cyclic codes will have a non-zero remainder, and all the samples in that codeword are deemed to be in error. The samples can be restored by taking the XOR of the remaining two codewords. If the error is in the parity words, no action is necessary. Further details of these recorders can be found in section 9.2. There is 100 percent redundancy in this unit, but it is designed to work with an existing video cassette recorder whose bandwidth is predetermined and so in this application there is no penalty.
The CRCC simply detects errors and acts as a pointer to a further correction means. This technique is often referred to as correction by erasure. The failing data is set to zero, or erased, since in some correction schemes the erroneous data will interfere with the calculation of the correct values.
===