Ultimate Guide to Digital Audio: Digital principles (part 1 of 3)

1. Pure binary code

For digital audio use, the prime purpose of binary numbers is to express the values of the samples which represent the original analog sound velocity or pressure waveform. FIG. 1 shows some binary numbers and their equivalent in decimal. The radix point has the same significance in binary: symbols to the right of it represent one half, one quarter and so on. Binary is convenient for electronic circuits, which do not get tired, but numbers expressed in binary become very long, and writing them is tedious and error-prone. The octal and hexadecimal notations are both used for writing binary since conversion is so simple. FIG. 1 also shows that a binary number is split into groups of three or four digits starting at the least significant end, and the groups are individually converted to octal or hexadecimal digits. Since sixteen different symbols are required in hex, the letters A-F are used for the numbers above nine.

FIG. 1 (a) Binary and decimal. (b) In octal, groups of three bits make one symbol 0-7. (c) In hex, groups of four bits make one symbol 0-F. Note how much shorter the number is in hex.

FIG. 2 Offset binary coding is simple but causes problems in digital audio processing. It is seldom used.

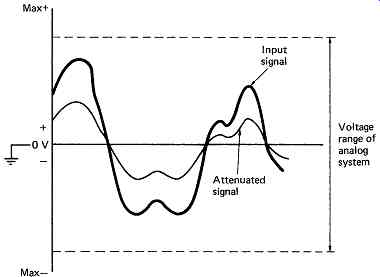
FIG. 3 Attenuation of an audio signal takes place with respect to midrange.

There will be a fixed number of bits in a PCM audio sample, and this number determines the size of the quantizing range. In the sixteen-bit samples used in much digital audio equipment, there are 65 536 different numbers. Each number represents a different analog signal voltage, and care must be taken during conversion to ensure that the signal does not go outside the convertor range, or it will be clipped. In FIG. 2 it will be seen that in a sixteen-bit pure binary system, the number range goes from 0000 hex, which represents the largest negative voltage, through 7FFF hex, which represents the smallest negative voltage, through 8000 hex, which represents the smallest positive voltage, to FFFF hex, which represents the largest positive voltage. Effectively, the zero voltage level of the audio has been shifted so that the positive and negative voltages in a real audio signal can be expressed by binary numbers which are only positive. This approach is called offset binary, and is perfectly acceptable where the signal has been digitized only for recording or transmission from one place to another, after which it will be converted directly back to analog. Under these conditions it is not necessary for the quantizing steps to be uniform, provided both ADC and DAC are constructed to the same standard. In practice, it is the requirements of signal processing in the digital domain which make both non-uniform quantizing and offset binary unsuitable.

FIG. 3 shows that an audio signal voltage is referred to midrange.

The level of the signal is measured by how far the waveform deviates from midrange, and attenuation, gain and mixing all take place around that midrange. Audio mixing is achieved by adding sample values from two or more different sources, but unless all the quantizing intervals are of the same size, the sum of two sample values will not represent the sum of the two original analog voltages. Thus sample values which have been obtained by non-uniform quantizing cannot readily be processed.

If two offset binary sample streams are added together in an attempt to perform digital mixing, the result will be that the offsets are also added and this may lead to an overflow. Similarly, if an attempt is made to attenuate by, say, 6.02 dB by dividing all the sample values by two, FIG. 4 shows that the offset is also divided and the waveform suffers a shifted baseline. The problem with offset binary is that it works with reference to one end of the range. What is needed is a numbering system which operates symmetrically with reference to the centre of the range.

FIG. 4 The result of an attempted attenuation in pure binary code is an offset. Pure binary cannot be used for digital audio processing.

2. Two's complement

In the two's complement system, the upper half of the pure binary number range has been redefined to represent negative quantities. If a pure binary counter is constantly incremented and allowed to overflow, it will produce all the numbers in the range permitted by the number of available bits, and these are shown for a four-bit example drawn around the circle in FIG. 5. As a circle has no real beginning, it is possible to consider it to start wherever it is convenient. In two's complement, the quantizing range represented by the circle of numbers does not start at zero, but starts on the diametrically opposite side of the circle. Zero is midrange, and all numbers with the MSB (most significant bit) set are considered negative. The MSB is thus the equivalent of a sign bit where 1 = minus. Two's complement notation differs from pure binary in that the most significant bit is inverted in order to achieve the half-circle rotation.

FIG. 5 In this example of a four-bit two's complement code, the number range is from - 8 to +7. Note that the MSB determines polarity.

FIG. 6 A two's complement ADC. At (a) an analog offset voltage equal to one-half the quantizing range is added to the bipolar analog signal in order to make it unipolar as at (b). The ADC produces positive-only numbers at (c), but the MSB is then inverted at (d) to give a two's complement output.

FIG. 7 Using two's complement arithmetic, single values from two waveforms are added together with respect to midrange to give a correct mixing function.

FIG. 6 shows how a real ADC is configured to produce two's complement output. At (a) an analog offset voltage equal to one half the quantizing range is added to the bipolar analog signal in order to make it unipolar as at (b). The ADC produces positive only numbers at (c) which are proportional to the input voltage. The MSB is then inverted at (d) so that the all-zeros code moves to the centre of the quantizing range.

The analog offset is often incorporated into the ADC as is the MSB inversion. Some convertors are designed to be used in either pure binary or two's complement mode. In this case the designer must arrange the appropriate DC conditions at the input. The MSB inversion may be selectable by an external logic level.

The two's complement system allows two sample values to be added, or mixed in audio parlance, and the result will be referred to the system midrange; this is analogous to adding analog signals in an operational amplifier. FIG. 7 illustrates how adding two's complement samples simulates the audio mixing process. The waveform of input A is depicted by solid black samples, and that of B by samples with a solid outline. The result of mixing is the linear sum of the two waveforms obtained by adding pairs of sample values. The dashed lines depict the output values.

Beneath each set of samples is the calculation which will be seen to give the correct result. Note that the calculations are pure binary. No special arithmetic is needed to handle two's complement numbers.

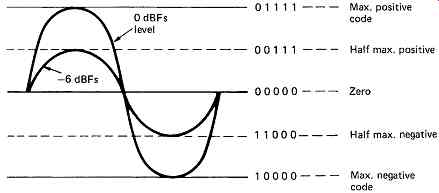
FIG. 8: 0dBFs is defined as the level of the largest sinusoid which will fit into the quantizing range without clipping.

FIG. 8 shows some audio waveforms at various levels with respect to the coding values. Where an audio waveform just fits into the quantizing range without clipping it has a level which is defined as 0 dBFs where Fs indicates full scale. Reducing the level by 6.02 dB makes the signal half as large and results in the second bit in the sample becoming the same as the sign bit. Reducing the level by a further 6.02 dB to -12 dBFs will make the second and third bits the same as the sign bit and so on. If a signal at -36 dBFs is input to a sixteen-bit system, only ten bits will be active, the remainder will copy the sign bit. For the best performance, analog inputs to digital systems must have sufficient levels to exercise the whole quantizing range.

It is often necessary to phase reverse or invert an audio signal, for example a microphone input to a mixer. The process of inversion in two's complement is simple. All bits of the sample value are inverted to form the one's complement, and one is added. This can be checked by mentally inverting some of the values in FIG. 5. The inversion is transparent and performing a second inversion gives the original sample values.

Using inversion, signal subtraction can be performed using only adding logic. The inverted input is added to perform a subtraction, just as in the analog domain. This permits a significant saving in hardware complexity, since only carry logic is necessary and no borrow mechanism need be supported.

In summary, two's complement notation is the most appropriate scheme for bipolar signals, and allows simple mixing in conventional binary adders. It is in virtually universal use in digital audio processing, and is accordingly adopted by all the major digital audio interfaces and recording formats.

Two's complement numbers can have a radix point and bits below it just as pure binary numbers can. It should, however, be noted that in two's complement, if a radix point exists, numbers to the right of it are added. For example, 1100.1 is not -4.5, it is -4 + 0.5 = -3.5.

3. Introduction to digital processing

However complex a digital process, it can be broken down into smaller stages until finally one finds that there are really only two basic types of element in use. FIG. 9 shows that the first type is a logical element.

This produces an output which is a logical function of the input with minimal delay. The second type is a storage element which samples the state of the input(s) when clocked and holds or delays that state. The strength of binary logic is that the signal has only two states, and considerable noise and distortion of the binary waveform can be tolerated before the state becomes uncertain. At every logical element, the signal is compared with a threshold, and can thus can pass through any number of stages without being degraded. In addition, the use of a storage element at regular locations throughout logic circuits eliminates time variations or jitter.

FIG. 9 Logic elements have a finite propagation delay between input and output and cascading them delays the signal an arbitrary amount. Storage elements sample the input on a clock edge and can return a signal to near coincidence with the system clock.

This is known as reclocking. Reclocking eliminates variations in propagation delay in logic elements.

FIG. 9 shows that if the inputs to a logic element change, the output will not change until the propagation delay of the element has elapsed.

However, if the output of the logic element forms the input to a storage element, the output of that element will not change until the input is sampled at the next clock edge. In this way the signal edge is aligned to the system clock and the propagation delay of the logic becomes irrelevant.

The process is known as reclocking.

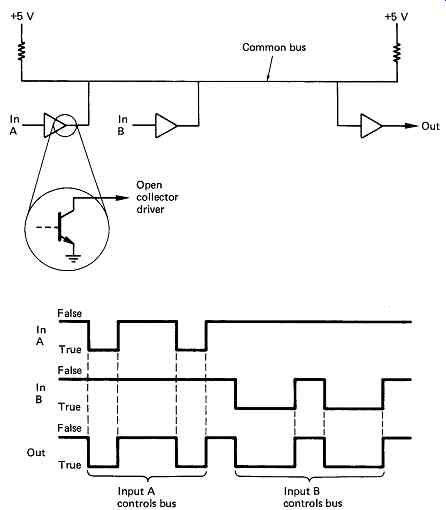
FIG. 10 Using open-collector drive, several signal sources can share one common bus. If negative logic is used, the bus drivers turn off their output transistors with a false input, allowing another driver to control the bus. This will not happen with positive logic.

4. Logic elements

The two states of the signal when measured with an oscilloscope are simply two voltages, usually referred to as high and low. The actual voltage levels will depend on the type of logic family in use, and on the supply voltage used. Within logic, these levels are not of much consequence, and it is only necessary to know them when interfacing between different logic families or when driving external devices.

The pure logic designer is not interested at all in the precise signal voltages, only in their meaning. Just as the electrical waveform from a microphone represents sound velocity, so the waveform in a logic circuit represents the truth of some statement. As there are only two states, there can only be true or false meanings. The true state of the signal can be assigned by the designer to either voltage state. When a high voltage represents a true logic condition and a low voltage represents a false condition, the system is known as positive logic, or high true logic. This is the usual system, but sometimes the low voltage represents the true condition and the high voltage represents the false condition. This is known as negative logic or low true logic. Provided that everyone is aware of the logic convention in use, both work equally well.

Negative logic was found in the TTL (transistor-transistor logic) family, because in this technology it was easier to sink current to ground than to source it from the power supply. FIG. 10 shows that if it is necessary to connect several logic elements to a common bus so that any one can communicate with any other, an open collector system is used, where high levels are provided by pull-up resistors and the logic elements only pull the common line down. If positive logic were used, when no device was operating the pull-up resistors would cause the common line to take on an absurd true state; whereas if negative logic is used, the common line pulls up to a sensible false condition when there is no device using the bus. Whilst the open collector is a simple way of obtaining a shared bus system, it is limited in frequency of operation due to the time constant of the pull-up resistors charging the bus capacitance. In the so called tri-state bus systems, there are both active pull-up and pull-down devices connected in the so-called totem-pole output configuration. Both devices can be disabled to a third state, where the output assumes a high impedance, allowing some other driver to determine the bus state.

FIG. 11 The basic logic gates compared.

In logic systems, all logical functions, however complex, can be configured from combinations of a few fundamental logic elements or gates. It is not profitable to spend too much time debating which are the truly fundamental ones, since most can be made from combinations of others. FIG. 11 shows the important simple gates and their derivatives, and introduces the logical expressions to describe them, which can be compared with the truth-table notation. The figure also shows the important fact that when negative logic is used, the OR gate function interchanges with that of the AND gate. Sometimes schematics are drawn to reflect which voltage state represents the true condition. In the so called intentional logic scheme, a negative logic signal always starts and ends at an inverting 'bubble'. If an AND function is required between two negative logic signals, it will be drawn as an AND symbol with bubbles on all the terminals, even though the component used will be a positive logic OR gate. Opinions vary on the merits of intentional logic.

If numerical quantities need to be conveyed down the two-state signal paths described here, then the only appropriate numbering system is binary, which has only two symbols, 0 and 1. Just as positive or negative logic could be used for the truth of a logical binary signal, it can also be used for a numerical binary signal. Normally, a high voltage level will represent a binary 1 and a low voltage will represent a binary 0, described as a 'high for a one' system. Clearly a 'low for a one' system is just as feasible. Decimal numbers have several columns, each of which represents a different power of ten; in binary the column position specifies the power of two.

Several binary digits or bits are needed to express the value of a binary audio sample. These bits can be conveyed at the same time by several signals to form a parallel system, which is most convenient inside equipment because it is fast, or one at a time down a single signal path, which is slower, but convenient for cables between pieces of equipment because the connectors require fewer pins. When a binary system is used to convey numbers in this way, it can be called a digital system.

5. Storage elements

The basic memory element in logic circuits is the latch, which is constructed from two gates as shown in FIG. 12(a), and which can be set or reset. A more useful variant is the D-type latch shown at (b) which remembers the state of the input at the time a separate clock either changes state for an edge-triggered device, or after it goes false for a level triggered device. D-type latches are commonly available with four or eight latches to the chip. A shift register can be made from a series of latches by connecting the Q output of one latch to the D input of the next and connecting all the clock inputs in parallel. Data are delayed by the number of stages in the register. Shift registers are also useful for converting between serial and parallel data transmissions.

Where large numbers of bits are to be stored, cross-coupled latches are less suitable because they are more complicated to fabricate inside integrated circuits than dynamic memory, and consume more current.

In large random access memories (RAMs), the data bits are stored as the presence or absence of charge in a tiny capacitor as shown in FIG. 12(c). The capacitor is formed by a metal electrode, insulated by a layer of silicon dioxide from a semiconductor substrate, hence the term MOS (metal oxide semiconductor). The charge will suffer leakage, and the value would become indeterminate after a few milliseconds. Where the delay needed is less than this, decay is of no consequence, as data will be read out before they have had a chance to decay. Where longer delays are necessary, such memories must be refreshed periodically by reading the bit value and writing it back to the same place. Most modern MOS RAM chips have suitable circuitry built in. Large RAMs store thousands of bits, and it is clearly impractical to have a connection to each one. Instead, the desired bit has to be addressed before it can be read or written. The size of the chip package restricts the number of pins available, so that large memories use the same address pins more than once. The bits are arranged internally as rows and columns, and the row address and the column address are specified sequentially on the same pins.

FIG. 12 Digital semiconductor memory types. In (a), one data bit can be stored in a simple set-reset latch, which has little application because the D-type latch in (b) can store the state of the single data input when the clock occurs. These devices can be implemented with bipolar transistors of FETs, and are called static memories because they can store indefinitely. They consume a lot of power.

In (c), a bit is stored as the charge in a potential well in the substrate of a chip. It is accessed by connecting the bit line with the field effect from the word line. The single well where the two lines cross can then be written or read. These devices are called dynamic RAMs because the charge decays, and they must be read and rewritten (refreshed) periodically.

FIG. 13 (a) Half adder; (b) full-adder circuit and truth table; (c) comparison of sign bits prevents wraparound on adder overflow by substituting clipping level.

6. Binary adding

The binary circuitry necessary for adding two's complement numbers is shown in FIG. 13. Addition in binary requires two bits to be taken at a time from the same position in each word, starting at the least significant bit. Should both be ones, the output is zero, and there is a carry-out generated. Such a circuit is called a half adder, shown in FIG. 13(a) and is suitable for the least-significant bit of the calculation. All higher stages will require a circuit which can accept a carry input as well as two data inputs. This is known as a full adder (b). Multibit full adders are available in chip form, and have carry-in and carry-out terminals to allow them to be cascaded to operate on long wordlengths. Such a device is also convenient for inverting a two's complement number, in conjunction with a set of invertors. The adder chip has one set of inputs grounded, and the carry-in permanently held true, such that it adds one to the one's complement number from the invertor.

When mixing by adding sample values, care has to be taken to ensure that if the sum of the two sample values exceeds the number range the result will be clipping rather than wraparound. In two's complement, the action necessary depends on the polarities of the two signals. Clearly if one positive and one negative number are added, the result cannot exceed the number range. If two positive numbers are added, the symptom of positive overflow is that the most significant bit sets, causing an erroneous negative result, whereas a negative overflow results in the most significant bit clearing. The overflow control circuit will be designed to detect these two conditions, and override the adder output. If the MSB of both inputs is zero, the numbers are both positive, thus if the sum has the MSB set, the output is replaced with the maximum positive code (0111. . .). If the MSB of both inputs is set, the numbers are both negative, and if the sum has no MSB set, the output is replaced with the maximum negative code (1000. . .). These conditions can also be connected to warning indicators. FIG. 13(c) shows this system in hardware. The resultant clipping on overload is sudden, and sometimes a PROM is included which translates values around and beyond maximum to soft clipped values below or equal to maximum.

A storage element can be combined with an adder to obtain a number of useful functional blocks which will crop up frequently in audio equipment. FIG. 14(a) shows that a latch is connected in a feedback loop around an adder. The latch contents are added to the input each time it is clocked. The configuration is known as an accumulator in computation because it adds up or accumulates values fed into it. In filtering, it is known as a discrete time integrator. If the input is held at some constant value, the output increases by that amount on each clock.

The output is thus a sampled ramp.

FIG. 14(b) shows that the addition of an invertor allows the difference between successive inputs to be obtained. This is digital differentiation. The output is proportional to the slope of the input.

FIG. 14 Two configurations which are common in processing. In (a) the feedback around the adder adds the previous sum to each input to perform accumulation or digital integration. In (b) an invertor allows the difference between successive inputs to be computed. This is differentiation.

7. The computer

The computer is now a vital part of digital audio systems, being used both for control purposes and to store, access and process audio signals as data. In control, the computer finds applications in database management, automation, editing, and in electromechanical systems such as synchronizers. Some time ago, processing speeds advanced sufficiently to allow computers to manipulate digital audio in real time.

The computer is a programmable device in that its operation is not determined by its construction alone, but instead by a series of instructions forming a program. The program is supplied to the computer one instruction at a time so that the desired sequence of events takes place.

Programming of this kind has been used for over a century in electromechanical devices, including automated knitting machines and street organs which are programmed by punched cards. However, today's computers differ from these devices in that the program is not fixed, but can be modified by the computer itself. This possibility led to the creation of the term software to suggest a contrast to the constancy of hardware.

Computer instructions are binary numbers each of which is interpreted in a specific way. As these instructions don't differ from any other kind of data, they can be stored in RAM. The computer can change its own instructions by accessing the RAM. Most types of RAM are volatile, in that they lose data when power is removed. Clearly if a program is entirely stored in this way, the computer will not be able to recover from a power failure. The solution is that a very simple starting or bootstrap program is stored in non-volatile ROM which will contain instructions which will bring in the main program from a storage system such as a disk drive after power is applied. As programs in ROM cannot be altered, they are sometimes referred to as firmware to indicate that they are classified between hardware and software.

Making a computer do useful work requires more than simply a program which performs the required computation. There is also a lot of mundane activity which does not differ significantly from one program to the next. This includes deciding which part of the RAM will be occupied by the program and which by the data, producing commands to the storage disk drive to read the input data from a file and write back the results. It would be very inefficient if all programs had to handle these processes themselves. Consequently the concept of an operating system was developed. This manages all the mundane decisions and creates an environment in which useful programs or applications can execute.

The ability of the computer to change its own instructions makes it very powerful, but it also makes it vulnerable to abuse. Programs exist which are deliberately written to do damage. These viruses are generally attached to plausible messages or data files and enter computers through storage media or communications paths.

There is also the possibility that programs contain logical errors such that in certain combinations of circumstances the wrong result is obtained. If this results in the unwitting modification of an instruction, the next time that instruction is accessed the computer will crash. In consumer-grade software, written for the vast personal computer market, this kind of thing is unfortunately accepted.

For critical applications, software must be verified. This is a process which can prove that a program can recover from absolutely every combination of circumstances and keep running properly. This is a non trivial process, because the number of combinations of states a computer can get into is staggering. As a result most software is unverified.

FIG. 15 A simple computer system. All components are linked by a single data/address/control bus. Although cheap and flexible, such a bus can only make one connection at a time, so it is slow.

It is of the utmost importance that networked computers which can suffer virus infection or computers running unverified software are never used in a life-support or critical application.

FIG. 15 shows a simple computer system. The various parts are linked by a bus which allows binary numbers to be transferred from one place to another. This will generally use tri-state logic (see section 4) so that when one device is sending to another, all other devices present a high impedance to the bus.

The ROM stores the startup program, the RAM stores the operating system, applications programs and the data to be processed. The disk drive stores large quantities of data in a non-volatile form. The RAM only needs to be able to hold part of one program as other parts can be brought from the disk as required. A program executes by fetching one instruction at a time from the RAM to the processor along the bus.

The bus also allows keyboard/mouse inputs and outputs to the display and printer. Inputs and outputs are generally abbreviated to I/O. Finally a programmable timer will be present which acts as a kind of alarm clock for the processor.

8. The processor

The processor or CPU (central processing unit) is the heart of the system.

FIG. 16 shows the data path of a simple CPU. The CPU has a bus interface which allows it to generate bus addresses and input or output data. Sequential instructions are stored in RAM at contiguously increasing locations so that a program can be executed by fetching instructions from a RAM address specified by the program counter (PC) to the instruction register in the CPU. As each instruction is completed, the PC is incremented so that it points to the next instruction. In this way the time taken to execute the instruction can vary.

The processor is notionally divided into data paths and control paths.

The CPU contains a number of general-purpose registers or scratchpads which can be used to store partial results in complex calculations. Pairs of these registers can be addressed so that their contents go to the ALU (arithmetic logic unit). This performs various arithmetic (add, subtract, etc.) or logical (AND, OR, etc.) functions on the input data. The output of the ALU may be routed back to a register or output. By reversing this process it is possible to get data into the registers from the RAM. The ALU also outputs the conditions resulting from the calculation, which can control conditional instructions.

FIG. 16 The data path of a simple CPU. Under control of an instruction, the ALU will perform some function on a pair of input values from the registers and store or output the result.

Which function the ALU performs and which registers are involved are determined by the instruction currently in the instruction register which is decoded in the control path. One pass through the ALU can be completed in one cycle of the processor's clock. Instructions vary in complexity as do the number of clock cycles needed to complete them.

Incoming instructions are decoded and used to access a look-up table which converts them into microinstructions, one of which controls the CPU at each clock cycle.

9. Interrupts

Ordinarily instructions are executed in the order that they are stored in RAM. However, some instructions direct the processor to jump to a new memory location. If this is a jump to an earlier instruction, the program will enter a loop. The loop must increment a count in a register each time, and contain a conditional instruction called a branch, which allows the processor to jump out of the loop when a predetermined count is reached.

However, it is often required that the sequence of execution should be changeable by some external event. This might be the changing of some value due to a keyboard input. Events of this kind are handled by interrupts, which are created by devices needing attention. FIG. 17 shows that in addition to the PC, the CPU contains another dedicated register called the stack pointer. FIG. 18 shows how this is used. At the end of every instruction the CPU checks to see if an interrupt is asserted on the bus.

FIG. 17 Normally the program counter (PC) increments each time an instruction is completed in order to select the next instruction. However, an interrupt may cause the PC state to be stored in the stack area of RAM prior to the PC being forced to the start address of the interrupt subroutine. Afterwards the PC can get its original value back by reading the stack.

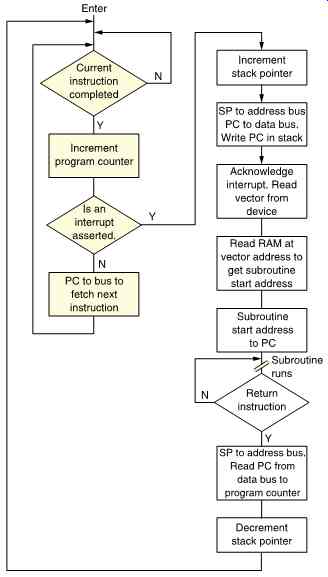
FIG. 18 How an interrupt is handled. See text for details.

If it is, a different set of microinstructions are executed. The PC is incremented as usual, but the next instruction is not executed. Instead, the contents of the PC are stored so that the CPU can resume execution when it has handled the current event. The PC state is stored in a reserved area of RAM known as the stack, at an address determined by the stack pointer.

Once the PC is stacked, the processor can handle the interrupt. It issues a bus interrupt acknowledge, and the interrupting device replies with a unique code identifying itself. This is known as a vector which steers the processor to a RAM address containing a new program counter. This is the RAM address of the first instruction of the subroutine which is the program that will handle the interrupt. The CPU loads this address into the PC and begins execution of the subroutine.

At the end of the subroutine there will be a return instruction. This causes the CPU to use the stack pointer as a memory address in order to read the return PC state from the stack. With this value loaded into the PC, the CPU resumes execution where it left off.

The stack exists so that subroutines can themselves be interrupted. If a subroutine is executing when a higher-priority interrupt occurs, the subroutine can be suspended by incrementing the stack pointer and storing the current PC in the next location in the stack.

When the second interrupt has been serviced, the stack pointer allows the PC of the first subroutine to be retrieved. Whenever a stack PC is retrieved, the stack pointer decrements so that it always points to the PC of the next item of unfinished business.

10. Programmable timers

Ordinarily processors have no concept of time and simply execute instructions as fast as their clock allows. This is fine for general-purpose processing, but not for time-critical processes such as audio. One way in which the processor can be made time conscious is to use programmable timers. These are devices which reside on the computer bus and which run from a clock. The CPU can set up a timer by loading it with a count.

When the count is reached, the timer will interrupt. To give an example, if the count were to be equal to one audio sample period, there would be one interrupt per sample, and this would result in the execution of a subroutine once per sample, provided, of course, that all the instructions could be executed in time.

11. Timebase compression and correction

In section 1 it was stated that a strength of digital technology is the ease with which delay can be provided. Accurate control of delay is the essence of timebase correction, necessary whenever the instantaneous time of arrival or rate from a data source does not match the destination.

In digital audio, the destination will almost always have perfectly regular timing, namely the sampling rate clock of the final DAC. Timebase correction consists of aligning jittery signals from storage media or transmission channels with that stable reference. In this way, wow and flutter are rendered unmeasurable.

A further function of timebase correction is to reverse the time compression applied prior to recording or transmission. As was shown in program that will handle the interrupt. The CPU loads this address into the PC and begins execution of the subroutine.

At the end of the subroutine there will be a return instruction. This causes the CPU to use the stack pointer as a memory address in order to read the return PC state from the stack. With this value loaded into the PC, the CPU resumes execution where it left off.

The stack exists so that subroutines can themselves be interrupted. If a subroutine is executing when a higher-priority interrupt occurs, the subroutine can be suspended by incrementing the stack pointer and storing the current PC in the next location in the stack.

When the second interrupt has been serviced, the stack pointer allows the PC of the first subroutine to be retrieved. Whenever a stack PC is retrieved, the stack pointer decrements so that it always points to the PC of the next item of unfinished business.

10. Programmable timers

Ordinarily processors have no concept of time and simply execute instructions as fast as their clock allows. This is fine for general-purpose processing, but not for time-critical processes such as audio. One way in which the processor can be made time conscious is to use programmable timers. These are devices which reside on the computer bus and which run from a clock. The CPU can set up a timer by loading it with a count.

When the count is reached, the timer will interrupt. To give an example, if the count were to be equal to one audio sample period, there would be one interrupt per sample, and this would result in the execution of a subroutine once per sample, provided, of course, that all the instructions could be executed in time.

11. Timebase compression and correction

In section 1 it was stated that a strength of digital technology is the ease with which delay can be provided. Accurate control of delay is the essence of timebase correction, necessary whenever the instantaneous time of arrival or rate from a data source does not match the destination.

In digital audio, the destination will almost always have perfectly regular timing, namely the sampling rate clock of the final DAC. Timebase correction consists of aligning jittery signals from storage media or transmission channels with that stable reference. In this way, wow and flutter are rendered unmeasurable.

A further function of timebase correction is to reverse the time compression applied prior to recording or transmission. As was shown in section 1.8, digital audio recorders compress data into blocks to facilitate editing and error correction as well as to permit head switching between blocks in rotary-head machines. Owing to the spaces between blocks, data arrive in bursts on replay, but must be fed to the output convertors in an unbroken stream at the sampling rate. The extreme time compression used in DAT to reduce the tape wrap is a further example of the use of the principle.

In computer hard-disk drives, which are used in digital audio editing systems, time compression is also used, but a converse problem also arises. Data from the disk blocks arrive at a reasonably constant rate, but cannot necessarily be accepted at a steady rate by the logic because of contention for the use of buses and memory by the different parts of the system. In this case the data must be buffered by a relative of the timebase corrector which is usually referred to as a silo.

Although delay is easily implemented, it is not possible to advance a data stream. Most real machines cause instabilities balanced about the correct timing: the output jitters between too early and too late. Since the information cannot be advanced in the corrector, only delayed, the solution is to run the machine in advance of real time. In this case, correctly timed output signals will need a nominal delay to align them with reference timing. Early output signals will receive more delay, and late output signals will receive less.

Section 2.5 showed the principles of digital storage elements which can be used for delay purposes. The shift-register approach and the RAM approach to delay are very similar, as a shift register can be thought of as a memory whose address increases automatically when clocked. The data rate and the maximum delay determine the capacity of the RAM required. Fig. 7 (section 1) showed that the addressing of the RAM is by a counter that overflows endlessly from the end of the memory back to the beginning, giving the memory a ring-like structure. The write address is determined by the incoming data, and the read address is determined by the outgoing data. This means that the RAM has to be able to read and write at the same time. The switching between read and write involves not only a data multiplexer but also an address multiplexer. In general the arbitration between read and write will be done by signals from the stable side of the TBC as FIG. 19 shows. In the replay case the stable clock will be on the read side. The stable side of the RAM will read a sample when it demands, and the writing will be locked out for that period. The input data cannot be interrupted in many applications, however, so a small buffer silo is installed before the memory, which fills up as the writing is locked out, and empties again as writing is permitted.

Alternatively, the memory will be split into blocks as was shown in section 1, such that when one block is reading a different block will be writing and the problem does not arise.

FIG. 19 In a RAM-based TBC, the RAM is reference synchronous, and an arbitrator decides when it will read and when it will write. During reading, asynchronous input data back up in the input silo, asserting a write request to the arbitrator. Arbitrator will then cause a write cycle between read cycles.

FIG. 20 Structure of FIFO of silo chip. Ripple logic controls propagation of data down silo.

FIG. 20 shows the operation of a FIFO chip, colloquially known as a silo because the data are tipped in at the top on delivery and drawn off at the bottom when needed. Each stage of the chip has a data register and a small amount of logic, including a data-valid or V bit. If the input register does not contain data, the first V bit will be reset, and this will cause the chip to assert 'input ready'. If data are presented at the input, and clocked into the first stage, the V bit will set, and the 'input ready' signal will become false. However, the logic associated with the next stage sees the V bit set in the top stage, and if its own V bit is clear, it will clock the data into its own register, set its own V bit, and clear the input V bit, causing 'input ready' to reassert, when another word can be fed in.

This process then continues as the word moves down the silo, until it arrives at the last register in the chip. The V bit of the last stage becomes the 'output ready' signal, telling subsequent circuitry that there are data to be read. If this word is not read, the next word entered will ripple down to the stage above. Words thus stack up at the bottom of the silo.

When a word is read out, an external signal must be provided which resets the bottom V bit. The 'output ready' signal now goes false, and the logic associated with the last stage now sees valid data above, and loads down the word when it will become ready again. The last register but one will now have no V bit set, and will see data above itself and bring that down. In this way a reset V bit propagates up the chip while the data ripple down, rather like a hole in a semiconductor going the opposite way to the electrons.

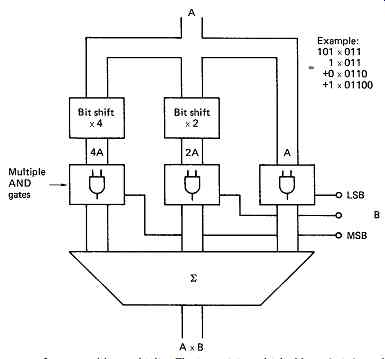
FIG. 21 Structure of fast multiplier. The input A is multiplied by 1, 2, 4, 8, etc. by bit shifting. The digits of the B input then determine which multiples of A should be added together by enabling AND gates between the shifters and the adder. For long wordlengths, the number of gates required becomes enormous, and the device is best implemented in a chip.

12. Gain control

When making a digital recording, the gain of the analog input will usually be adjusted so that the quantizing range is fully exercised in order to make a recording of maximum signal-to-noise ratio. During post-production, the recording may be played back and mixed with other signals, and the desired effect can only be achieved if the level of each can be controlled independently. Gain is controlled in the digital domain by multiplying each sample value by a coefficient. If that coefficient is less than one, attenuation will result; if it is greater than one, amplification can be obtained.

Multiplication in binary circuits is difficult. It can be performed by repeated adding, but this is too slow to be of any use. In fast multiplication, one of the inputs will be simultaneously multiplied by one, two, four, etc., by hard-wired bit shifting. FIG. 21 shows that the other input bits will determine which of these powers will be added to produce the final sum, and which will be neglected. If multiplying by five, the process is the same as multiplying by four, multiplying by one, and adding the two products. This is achieved by adding the input to itself shifted two places. As the wordlength of such a device increases, the complexity increases exponentially, so this is a natural application for an integrated circuit. It is probably true that digital video would not have been viable without such chips.

13. Digital faders and controls

In a digital mixer, the gain coefficients will originate in hand-operated faders, just as in analog. Analog mixers having automated mixdown employ a system similar to the one shown in FIG. 22. Here, the faders produce a varying voltage and this is converted to a digital code or gain coefficient in an ADC and recorded alongside the audio tracks. On replay the coefficients are converted back to analog voltages which control VCAs (voltage-controlled amplifiers) in series with the analog audio channels. A digital mixer has a similar structure, and the coefficients can be obtained in the same way. However, on replay, the coefficients are not converted back to analog, but remain in the digital domain and control multipliers in the digital audio channels directly. As the coefficients are digital, it is so easy to add automation to a digital mixer that there is not much point in building one without it.

FIG. 22 The automated mixdown system of an audio console digitizes fader positions for storage and uses the coefficients later to drive VCAs via convertors.

FIG. 23 An absolute linear fader uses a number of light beams which are interrupted in various combinations according to the position of a grating. A Gray code shown in FIG. 24 must be used to prevent false codes.

Whilst gain coefficients can be obtained by digitizing the output of an analog fader, it is also possible to obtain coefficients directly in digital faders. Digital faders are a form of displacement transducer in which the mechanical position of the knob is converted directly to a digital code.

The position of other controls, such as for equalizers or scrub wheels, will also need to be digitized. Controls can be linear or rotary, and absolute or relative. In an absolute control, the position of the knob determines the output directly. These are inconvenient in automated systems because unless the knob is motorized, the operator does not know the setting the automation system has selected. In a relative control, the knob can be moved to increase or decrease the output, but its absolute position is meaningless. The absolute setting is displayed on a bar LED nearby. In a rotary control, the bar LED may take the form of a ring of LEDs around the control. The automation system setting can be seen on the display and no motor is needed. In a relative linear fader, the control may take the form of an endless ridged belt like a caterpillar track. If this is transparent, the bar LED may be seen through it.

FIG. 23 shows an absolute linear fader. A grating is moved with respect to several light beams, one for each bit of the coefficient required.

The interruption of the beams by the grating determines which photocells are illuminated. It is not possible to use a pure binary pattern on the grating because this results in transient false codes due to mechanical tolerances. FIG. 24 shows some examples of these false codes. For example, on moving the fader from 3 to 4, the MSB goes true slightly before the middle bit goes false. This results in a momentary value of 4 + 2 = 6 between 3 and 4. The solution is to use a code in which only one bit ever changes in going from one value to the next. One such code is the Gray code, which was devised to overcome timing hazards in relay logic but is now used extensively in position encoders.

Gray code can be converted to binary in a suitable PROM or gate array.

These are available as industry-standard components.

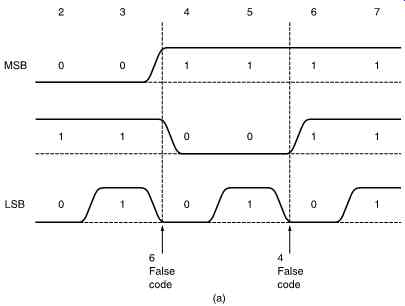
FIG. 24 (a) Binary cannot be used for position encoders because mechanical tolerances cause false codes to be produced. (b) In Gray code, only one bit (arrowed) changes in between positions, so no false codes can be generated.

FIG. 25 The fixed and rotating gratings produce moire fringes which are detected by two light paths as quadrature sinusoids. The relative phase determines the direction, and the frequency is proportional to speed of rotation.

FIG. 25 shows a rotary incremental encoder. This produces a sequence of pulses whose number is proportional to the angle through which it has been turned. The rotor carries a radial grating over its entire perimeter. This turns over a second fixed radial grating whose bars are not parallel to those of the first grating. The resultant moire fringes travel inward or outward depending on the direction of rotation. Two suitably positioned light beams falling on photocells will produce outputs in quadrature. The relative phase determines the direction and the frequency is proportional to speed. The encoder outputs can be connected to a counter whose contents will increase or decrease according to the direction the rotor is turned. The counter provides the coefficient output and drives the display.

For audio use, a logarithmic characteristic is required in gain control.

Linear coefficients can conveniently be converted to logarithmic in a PROM. The wordlength of the gain coefficients requires some thought as they determine the number of discrete gains available. If the coefficient wordlength is inadequate, the gain control becomes 'steppy' particularly towards the end of a fadeout. This phenomenon is quite noticeable on some low-cost home studio equipment. A compromise between performance and the expense of high-resolution faders is to insert a digital interpolator having a low-pass characteristic between the fader and the gain control stage. This will compute intermediate gains to higher resolution than the coarse fader scale so that the steps cannot be heard.

Digital filters used for equalization can also be sensitive to sudden step changes to their control coefficients. Again the solution is to filter the coefficients.

FIG. 26 One multiplier/accumulator can be time shared between several signals by operating at a multiple of sampling rate. In this example, four multiplications are performed during one sample period.

14. A digital mixer

The signal path of a simple digital mixer is shown in FIG. 26. The two inputs are multiplied by their respective coefficients, and added together in two's complement to achieve the mix as was shown in FIG. 7. Peak limiting will be required as in section 3.6. The sampling rate of the inputs must be exactly the same, and in the same phase, or the circuit will not be able to add on a sample-by-sample basis. If the inputs have come from different sources, they must be synchronized by the same master clock, and/or timebase correction must be provided on the inputs. Synchronization of audio sources follows the principle long established in video in which a reference signal is fed to all devices which then slave or genlock to it. This process will be covered in detail in section 8.

Some thought must be given to the wordlength of the system. If a sample is attenuated, it will develop bits which are below the radix point.

For example, if an eight-bit sample is attenuated by 24 dB, the sample value will be shifted four places down. Extra bits must be available within the mixer to accommodate this shift. Digital mixers can have an internal wordlength of up to 32 bits. When several attenuated sources are added together to produce the final mix, the result will be a stream of 32-bit or longer samples. As the output will generally need to be of the same format as the input, the wordlength must be shortened. This must be done very carefully, as it is a form of quantizing and will require dithering. The necessary techniques will be treated in section 4.

In practice a digital mixer would not have one multiplier for every input. Multiplier chips are expensive, but can work much faster than the relatively low frequencies used in audio sampling. FIG. 26 also shows that a more economical system results when a time-shared bus system is used with only one multiplier followed by an accumulator. In one sample period, each of the input samples is fed in turn to the lower input of the multiplier at the same time as the corresponding coefficient is fed to the upper input. The products from the multiplier are accumulated during the sample period, so that at the end of the sample period, the accumulator holds the sum of all the products, which is the digitally mixed sample. The process then repeats for the next sample period. To facilitate the sharing of common circuits by many signals, tri-state logic devices can be used. The outputs of such devices can be wired in parallel, and the state of the parallel connection will be the state of the device whose output is enabled. Clearly only one output can be enabled at a time, and this will be ensured by a sequencer circuit connected to all the device enables. In digital signal processor (DSP) chips, the processes shown above can be simulated in software.

In analog audio mixers, the controls have to be positioned close to the circuitry for performance reasons; thus one control knob is needed for every variable, and the control panel is physically large. Remote control is difficult with such construction. The order in which the signal passes through the various stages of the mixer is determined at the time of design, and any changes are difficult.

In a digital mixer, all the filters are controlled by simply changing the coefficients, and remote control is easy. Since control is by digital parameters, it is possible to use assignable controls, such that there need only be one set of filter and equalizer controls, whose setting is conveyed to any channel chosen by the operator.

The use of digital processing allows the console to include a video display of the settings. This was seldom attempted in analog desks because the magnetic field from the scan coils tended to break through into the audio circuitry.

Since the audio processing in a digital mixer is by program control, the configuration of the desk can be changed at will by running the programs for the various functions in a different order. The operator can configure the desk to his own requirements by entering symbols on a block diagram on the video display, for example. The configuration and the setting of all the controls can be stored in memory or for a longer term, on disk, and recalled instantly. Such a desk can be in almost constant use, because it can be put back exactly to a known state easily after someone else has used it.

A further advantage of working in the digital domain is that delay can be controlled individually in the audio channels.

This allows for the time of arrival of wavefronts at various microphones to be compensated despite their physical position.

FIG. 27 Digital mixer installation. The convenience of digital transmission without degradation allows the control panel to be physically remote from the processor.

FIG. 27 shows a typical digital mixer installation.

The analog microphone inputs are from remote units containing ADCs so that the length of analog cabling can be kept short. The input units communicate with the signal processor using digital fiber-optic links.

The sampling rate of a typical digital audio signal is low compared to the speed at which typical logic gates can operate. It is sensible to minimize the quantity of hardware necessary by making each perform many functions in one sampling period. Although general-purpose computers can be programmed to process digital audio, they are not really suitable for the following reasons:

1. The number of arithmetic operations in audio processing, particularly multiplications, is far higher than in data processing.

2. Audio processing is done in real time; data processors do not generally work in real time.

3. The program needed for an audio function generally remains constant for the duration of a session, or changes slowly, whereas a data processor rapidly jumps between many programs.

4. Data processors can suspend a program on receipt of an interrupt; audio processors must work continuously for long periods.

5. Data processors tend to be I/O limited, in that their operating speed is limited by the problems of moving large quantities of data and instructions into the CPU. Audio processors in contrast have a relatively small input and output rate, but compute intensively.

The above is a sufficient case for the development of specialized digital audio signal processors.

These units are implemented with more internal registers than data processors to facilitate multi-point filter algorithms. The arithmetic unit will be designed to offer high-speed multiply/accumulate using techniques such as pipelining, which allows operations to overlap.

The functions of the register set and the arithmetic unit are controlled by a microsequencer.

External control of a DSP will generally be by a smaller processor, often in the operator's console, which passes coefficients to the DSP as the operator moves the controls. In large systems, it is possible for several different consoles to control different sections of the DSP.

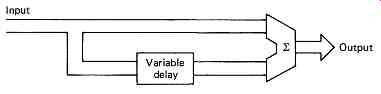
FIG. 28 (a) A simple configuration to obtain digital echo. The delay would normally be several tens of milliseconds. If the delay is made about 10 ms, the configuration acts as a comb filter, and if the delay is changed dynamically, a notch will sweep the audio spectrum resulting in flanging.

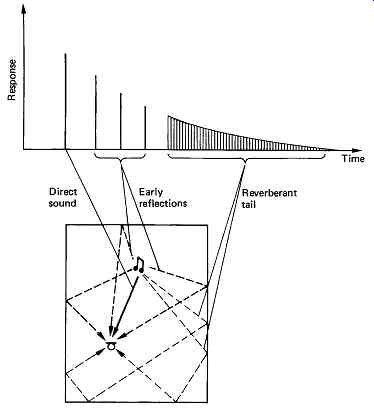
FIG. 28 (b) In a reverberant room, the signal picked up by a microphone is a mixture of direct sound, early reflections and a highly confused reverberant tail. A digital reverberator will simulate this with various combinations of recursive delay and attenuation.

15. Effects

In addition to equalization and mixing, modern audio production requires numerous effects, and these can be performed in the digital domain by simply mimicking the analog equivalent.

One of the oldest effects is the use of a tape loop to produce an echo, and this can be implemented with memory or, for longer delays, with a disk drive. FIG. 28(a) shows the basic configuration necessary for echo. If the delay period is dynamically changed from zero to about 10ms, the result is flanging, where a notch sweeps through the audio spectrum. This was originally done by having two identical analog tapes running, and modifying the capstan speed with hand pressure! A relative of echo is reverberation, which is used to simulate ambience on an acoustically dry recording. FIG. 28(b) shows that reverberation actually consists of a series of distinct early reflections, followed by the reverberation proper, which is due to multiple reflections. The early reflections are simply provided by short delays, but the reverberation is more difficult. A recursive structure is a natural choice for a decaying response, but simple recursion sounds artificial. The problem is that, in a real room, standing waves and interference effects cause large changes in the frequency response at each reflection. The effect can be simulated in a digital reverberator by adding various comb-filter sections which have the required effect on the response.

FIG. 29 A phase-locked loop requires these components as a minimum. The filter in the control voltage serves to reduce clock jitter.

16. The phase-locked loop

All digital audio systems need to be clocked at the appropriate rate in order to function properly. Whilst a clock may be obtained from a fixed frequency oscillator such as a crystal, many operations in audio require genlocking or synchronizing the clock to an external source. The phase locked loop excels at this job, and many others, particularly in connection with recording and transmission.

In phase-locked loops, the oscillator can run at a range of frequencies according to the voltage applied to a control terminal. This is called a voltage-controlled oscillator or VCO. FIG. 29 shows that the VCO is driven by a phase error measured between the output and some reference. The error changes the control voltage in such a way that the error is reduced, so that the output eventually has the same frequency as the reference. A low-pass filter is fitted in the control voltage path to prevent the loop becoming unstable. If a divider is placed between the VCO and the phase comparator, as in the figure, the VCO frequency can be made to be a multiple of the reference. This also has the effect of making the loop more heavily damped, so that it is less likely to change frequency if the input is irregular.

FIG. 30 Obtaining a 48 kHz sampling clock from the line frequency of 625/50 video using a phase-locked loop.

In digital audio, the frequency multiplication of a phase-locked loop is extremely useful. FIG. 30 shows how the 48 kHz sampling clock is obtained from the sync pulses of a video reference by such a multiplication process.

FIG. 31 shows the NLL or numerically locked loop. This is similar to a phase-locked loop, except that the two phases concerned are represented by the state of a binary number. The NLL is useful to generate a remote clock from a master. The state of a clock count in the master is periodically transmitted to the NLL which will recreate the same clock frequency. The technique is used in MPEG transport streams.

FIG. 31 The numerically locked loop (NLL) is a digital version of the phase-locked loop.

cont to part 2 >>