FILTERS Á LA DIGITAL

Last month, as you might recall, filter a la analog was the main course on the menu at the Domain Restaurant. Although the cascaded passive design had a promising, traditional taste, we soon developed a dislike for the spicy phase shift and watery dispersion inherent in the recipe. I think we agreed that brick-wall fare perhaps wasn't appropriate for our more refined digital palates. We wondered: Is there some way of interfacing digital storage with the analog world, without using analog filters? The answer is no, and yes.
The Nyquist Theorem dictates that the input anti-aliasing filter be present before sampling occurs. In other words, filtering must take place on the analog signal before digitization be gins; thus, the input filter must be analog. We must carefully observe our de sign criteria to minimize dispersion, and perhaps employ time correction to compensate for phase shift.
The output anti-imaging filter is traditionally placed after the D/A converter; therefore, it, too, is an analog device.
But there's an alternative. It should be possible to implement filtering in the digital domain, before the D/A converter. Voila--digital filters or, as the technique is sometimes called, oversampling. With clever data manipulation we can alleviate the need for an output brick-wall filter.
The pulse amplitude modulation signal (staircase waveform) is the analog output signal of an audio digitization system. Those sharp staircase edges represent high-frequency content not present in the original audio waveform.
Specifically, this high-frequency con tent occurs as a series of image spectra, which are duplicates of the original, repeating endlessly, as shown in Fig. 1. It is the anti-imaging filter's job to smooth the waveform and thus re move these duplicate images, leaving only the original spectrum. Sharp-eyed readers might question the need to worry about frequencies such as 43 or 176 kHz, since they lie so far above the limits of audibility. The original wave form is reproduced without filtering, but the accompanying image bands cause intermodulation in downstream equipment through which it passes, and that in turn could add audible distortion to the signal.
Rather than suppress these high-frequency image components after the signal has been converted to analog form, it is possible to process the digitized signal before D/A conversion using an oversampler, a transversal filter, and a noise-shaper circuit. A block diagram of the technique, as implemented by Philips in their CD players, is shown in Fig. 2. In this circuit, the 16-bit, 44.1-kHz audio channels pass through a shift register, which oversamples them, multiplying the sampling frequency by, in this case, four.
As a result, the 44.1-kHz sampling frequency becomes 176.4 kHz. Four times as many samples are present after oversampling; the intermediate values are calculated at the transversal filter. The same shift register delays the samples so that, after multiplication by 12-bit coefficients and addition, the weighted average of a large number of samples is generated. The filter's coefficients produce a transition region be tween 20 and 24.3 kHz, and again around 176 kHz, which accomplishes the filtering. The overall effect is the suppression of the frequency bands between 20 and 156.4 kHz. As can be seen in Fig. 3, the bands centered at 44.1, 88.2, and 132.3 kHz no longer exist; thus, filtering has occurred. (The band around 176 kHz will be sup pressed in a later circuit stage.) Oversampling has an additional benefit: By oversampling four times, the noise power is distributed over a band four times as wide as that from which it was originally derived; in other words, the quantization noise from the band of 0 Hz to 22 kHz is extended over a band four times as wide, 0 Hz to 88 kHz. Since only the in-band noise affects us, we can say that only one-quarter of the quantization noise re mains. Thus, we are rewarded with a free 6-dB improvement in signal-to noise ratio.
The output from the transversal filter is a digital bit stream with a word length of 28 bits and a sampling frequency of 176 kHz. A digital noise-shaping circuit is used to improve the signal-to-noise ratio by 7 dB. The 28-bit samples are rounded off to 14 bits; the rounding off is delayed by one sampling interval and added back to the input signal. The result is that noise power is filtered so that quantization noise is no longer uniform over the band from 0 Hz to 88 kHz. In the audio band, from 0 Hz to 20 kHz, the noise power is greatly reduced, and above this band it is greatly increased, as shown in Fig. 4. That's totally satisfactory because only the in-band noise level concerns our ears.
Normally, rounding off the samples to 14 bits would yield a signal-to-noise ratio of 84 dB, but with our free 6 dB from oversampling, and our additional 7 dB from noise-shaping, we end up with a maximum S/N ratio of 97 dB. We can use a much cheaper (and less temperature-sensitive) 14-bit converter while rivaling the performance of everybody else's 16-bit converter. The information in the 15th and 16th bits of the signal are transferred to the 14th bit. Full 16-bit information capability is retained because the information capacity of the two "surplus" bits is transferred into the four-times-higher information-transmission level of the oversampled signal. In other words, the averaged value of the quarter-length, 14-bit samples is as accurate as that of 16-bit samples over the original sample period. (Parenthetically, I should mention that Philips uses a very ingenious converter design called dynamic element matching, with outstanding characteristics of its own.)
Our recipe for good sound does not include the image band around 176 kHz which the transversal filter did not remove. This is now suppressed-in the analog domain-by the combination of a sample-and-hold function with a (sin X)/X characteristic and an analog filter.
This anti-imaging filter follows the converter, just as in players without digital filtration. But it is tame compared to the brick-wall dishes we tasted last month. Since the band we must eradicate is so high in frequency, we can use a filter with a gentle, 12-dB/ octave curve and a-3 dB point be tween 30 and 40 kHz. It is a noncritical design; a third-order Bessel type might be employed. Its low order guarantees good phase linearity; phase distortion is reduced to ± 0.5° across the audio band. The bandwidth of the filter is also greater than the audio bandwidth.
Amplifiers have always had band widths much greater than "necessary"; now, digital designers are apparently following suit.
A digital filter design is thus an efficient method of accomplishing the task of anti-imaging without resorting to analog brick-wall filters. While many CD player manufacturers who still employ analog filters might disagree, digital oversampling seems to me to offer a more sophisticated solution. On the other hand, some manufacturers with oversampling designs are guilty of some highly misleading advertising; hey imply that the fourfold sampling rate automatically means higher fidelity. Of course, that is not true per se; as we have seen, oversampling is merely a technique internal to the digital filter.
In terms of sonic performance, does digital filtering do a better job than analog filtering? Do CD players with digital filters sound better than those with analog filters? After critical, blind listening, I think I incline toward the digital. I encourage all readers to try the test for yourselves; I guarantee it will give your sensibilities a real workout.
Perhaps the difference is so slight as to be merely a question of taste. Your check, sir.
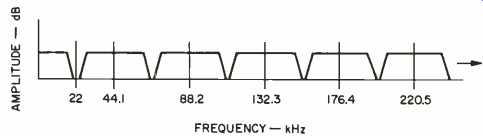
Fig. 1--Frequency spectrum of sampled output signal, showing periodic repetitions
of audio band at multiples of the sampling frequency.
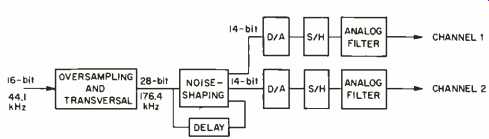
Fig. 2--Digital filtration.
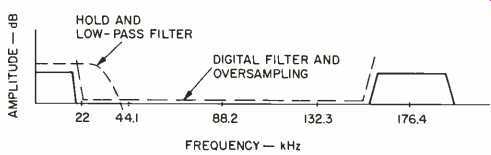
Fig. 3--Frequencies above the audio band are suppressed in two stages.
The bands surrounding 44.1, 88.2, and 132.3 kHz are removed by the transversal filter; the remaining band, centered at 176.4 kHz, is removed later by the sample-and-hold circuit and a gentle low-pass filter.
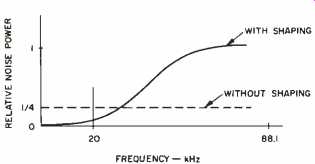
Fig. 4--Noise-shaping reduces noise within the audio band by increasing noise
at higher frequencies, which is later filtered out.
Reference
Van De Plassche, R. J., and E. C. Dijkmans, "A Monolithic 16-Bit D/A Conversion System for Digital Audio," presented at the Audio Engineering Society's Rye (N.Y.) Conference, June 1982.
(adapted from Audio magazine, Aug. 1985; KEN POHLMANN)
= = = =