
By Ron C. Johnson; C.E.T.
We said in the last issue that we were going to talk about magnetics this time. And possibly you are all wondering why we would want to know about magnetics for basic electricity. As my students often tell me, they wonder even more after they have wallowed around in this stuff for a while. It's true: magnetism and electromagnetism is a "cat's breakfast" of new terms, formulas and relationships (most of them non-linear) which can be confusing. On the other hand, an understanding of this area is not only useful, but necessary to make sense out of stuff like: inductors, relays, motors, tape recorders... The list goes on.
So we are going to take a run at it on a non-mathematical basis. And if the new terms start to come at you too fast and furious just kick back and imagine yourself listening to one of those foreign language instructional tapes with surf in the background. If it puts you to sleep I want to know.
Maybe I'll market it...
THE MAGNETIC FIELD
To start with we are not going to try to explain what magnetism is in its most fundamental form.
Call it one of those mysteries of the universe that only Phd's and people confined to institutions truly understand. For our purposes we want to know the how more than the why.
All of us are familiar with those strange new lifeforms which appear out of nowhere and then multiply on the doors of our refrigerators. Yes, the fridge magnet beings have insinuated themselves into the very fabric of our homes, attaching themselves to our appliances under the guise of grocery list holders, real estate advertisements and kindergarten crafts... What? Ah, yes...the magnetic field. Back to business.
MAGNETIC FLUX
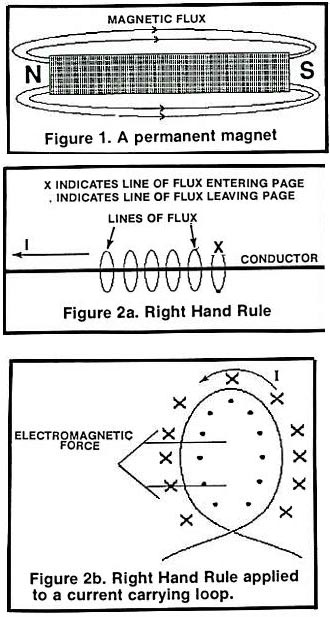
Figure 1. A permanent magnet
As I said, we are all familiar with magnetism from its various household uses and no doubt we have all played with magnets enough to have a first-hand knowledge of how they are attracted to objects with iron in them. We have also seen how bringing two magnets together will cause either attraction or repulsion depending on how they are oriented with respect of each other. Figure 1 shows a bar magnet with a set of lines (with arrows) extending out of one end and re-entering the other end. These lines are called lines of flux. You will notice that the lines of flux exit the end labeled N (for North) and re-enter the end labeled S (for South). The reason the ends, or poles, of the magnet are labeled North and South is that if the magnet were suspended freely the end labeled N would orient itself toward the magnetic North Pole of the earth (like a compass). The same force that causes this is the force that causes the attraction or repulsion between two magnets. When a North and a South pole are brought together they attract; when two North's or two South's are brought together they repel.
Yes, I know that this is nothing new to most of you but the basics bear repeating before we launch into the other good stuff. And there really is an application here: The magnets we are used to seeing are natural or synthetic magnets which are relatively weak. Also, we don't have much control over them other than moving them physically closer or farther away from an object. But if we could control those lines of flux (and the magnetic force that they produce) with electricity, we would be able to build a number of useful things such as: meter movements, relays, breakers, solenoids, motors, etc. (Love that word "etc." It covers a whole range of things I can't remember.)
Okay, let's look at Electromagnetism.
First a history lesson: History and yer Right Hand Rule
In 1820, the Danish physicist Hans Christian Oersted discovered (history always starts out the same way, doesn't it?) that the needle of a compass would deflect if brought near a current-carrying conductor. This proved that electricity and magnetism are related. Actually, what Hans proved was that a magnetic field always occurs in conjunction with current flow. The magnetic flux (same as the lines around a magnet) form concentric rings around the conductor and we can predict the direction of the lines (remember the arrows on the bar magnet lines of flux) by using the "good of basic" Right Hand Rule.
The Right Hand Rule is simple. If you were to imagine yourself holding a current carrying conductor in your right hand with your thumb pointing in the direction of conventional current flow (opposite of electron flow, remember), the rest of your fingers point in the direction of the lines of flux as they curve around the conductor. (See Figure 2a)
Figure 2a. Right Hand Rule
So that means that any conductor with current flowing through it will produce a magnetic field.
Is that important?
Figure 2b. Right Hand Rule applied to a current carrying loop.
Actually, the strength of the field is small in most cases but there is a way of putting that field to use and making it more powerful. Take a look at Figure 2b. At this point we have to start imagining what is happening in three dimensions. Let's use the convention that an "x" indicates a line of flux entering the page from above. A dot, ".", indicates a line of flux exiting the page. Figure 2b shows a loop of wire with current flowing through it. If we use the Right Hand Rule to determine the direction of the lines of flux and try to visualize it in three dimensions we will find that the lines from one side of the loop point in the same direction as the lines from the other side of the loop.
This causes the lines of flux to be concentrated in the middle of the loop. If we were to add several more loops all the lines would reinforce each other increasing the strength of the magnetic field.
That's what we have done in Figure 3. Not only have we used several turns of current carrying wire (supplied by the battery), but we have added a "core." The core is a ferrous material which concentrates the lines of flux. This increases what we call the "flux density" because there are more lines of flux in a smaller space. Up to a certain point increasing the flux density increases the "field strength" of the electromagnet, in other words making it a stronger magnet.

FIG. 3
SOME APPLICATIONS
Before we get into the nitty-gritty of all this, let's look at what it means in practical terms. As I said before, a single conductor with current flowing which creates a magnetic field around it doesn't accomplish much for us. But when we wind a number of turns of wire on a ferrous core and run current through we now have a fairly strong magnetic force produced.
Have you ever seen those electromagnets used in junk yards for moving wrecked cars around? That gives an idea of the amount of force that can be produced with an electromagnet. But we have lots of good examples closer to home.
Electric door latches used for security locks in apartment buildings are electromagnets. Normally a spring latching mechanism keeps the latch locked but when the button is pushed in the apartment current flows through the coil of an electromagnet in the latch pulling back a metal bolt which allows the door to be opened. For those of you who have experimented with relays the application is similar: The electromagnet, when energized, pulls in a metal linkage that forces the contacts together (or apart in some cases) positioning the relay contacts in the energized condition. (When you hear the term "normal" as in "normally open contacts" this means that the relay coil is not energized and the contacts are either open or closed when the relay is at rest.) Another application for electromagnets is solenoid valves. They are used in common household appliances like your dishwasher to control the water.
A valve is controlled by an electromagnet moving a ferrous plunger in or out of position. In this case the ferrous core of the electromagnet is not fixed in place but moves within the winding of the electromagnet when the line of flux acts on it.
Enough of that. Let's look at some of the characteristics of the electromagnetic field and how we use them. As I said before, there are lots of new terms.
Outstanding in yer Magnetic Field
We said that magnetic force, (which we call magnetomotive force, similar to electric force called electromotive force), is developed by winding a current carrier around a core. The amount of magnetomotive force (mmf), then, is determined by the number of turns, (N) and the amount of current flowing, (I). Increase either and the mmf increases.
The symbol is F, and the units are ampere-turns.
F=N x I
In magnetic circuits the lines of flux are analogous to current in an electric circuit. Flux is symbolized by cl), (phi) and has the unit, Webers. (Don't ask me why, I jus' does as l's tol'.) Again, I said that by choosing a ferrous core we could concentrate the flux. This is because various materials have different abilities to set up magnetic lines of force. This ability is called permeance, (p) and the units are Henrys. Quite often we use the reciprocal of permeance instead, which is called reluctance. We would have to define reluctance then as the opposition to the setting up of magnetic lines of flux. Compare that to resistance in electric circuits. Reluctance is symbolized by R and is usually expressed in "per Henrys." (In other words the reciprocal of Henrys)
Keep in mind that I warned you! And it gets worse.
Take a deep breath... So permeance and reluctance are reciprocals.
Believe it or not, so are permeability and reluctivity, but don't worry, we don't use these much. If you are interested, reluctivity is the magnetic equivalent to resistivity (in electricity) that we talked about way back when in the first article of this series. Resistivity, we said, was the characteristic of a material that determined how well it conducted electricity, and hence, determined the resistance of a particular shape and size of the material. Well, reluctivity is the characteristic of a material which determines how well it sets up lines of flux and hence, the reluctance or a given piece of that material. In this case we most often use permeability, the reciprocal of reluctivity, which is symbolized, p, and has the units, Henry/ meter.
Now that we have looked at flux and reluctance we can backtrack and look at how they relate to magnetomotive force. We know about Ohm's Law from electricity; here is its equivalent in magnetics: Ampere's Circuital Law.
Ampere's Circuital Law says that magnetomotive force equals the magnetic flux, (e), times the reluctance of the material, (R) or: F= R This operates in the same way as Ohm's Law. For various materials in a magnetic circuit (which have different reluctances), the amount of flux present in that section times the reluctance will give the magnetomotive force developed across that section.
The same relationships we talked about with respect to Kirchhoff's Voltage Law around a loop apply around a magnetic loop and series and parallel principles apply in the same way. (Figure 4)

Fig. 4---DIFFERENT PERMEABILITY OF MATERIALS GIVES DIFFERENT RELUCTANCE
FOR EACH SECTION
Not that it matters...
Actually, you won't find hobbyists, technicians, technologists or even very many engineers use this stuff quantitatively in practical applications. Designing transformers or other special magnetic equipment would require it, but usually we just buy that kind of thing with ready-made specifications available. Even so, the concepts are interesting and help to understand what is going on. In fact, as we continue, we'll see how they help us understand some very practical applications.
Coffee's over. Back to work.
Magnetic Field Strength
We all know that when we move a magnet closer to a ferrous object the pull is greater than when it is farther away. How strong the force of that "pull" is can be expressed as magnetic field strength (or intensity) and is symbolized, H, with units, Oersteds. (Well, they had to name something after the guy.) It is determined by the magnetomotive force, (F) divided by the distance, (1).
H=F/1
Another important variable in magnetics is called magnetic field density or flux density, (B), given in Teslas. (Some other guy who, incidentally, also liked to play with high voltage.) Basically, flux density is the number of magnetic lines of force per unit area, (A). (If you go back and sort through some of the previous stuff, you would find that the number of lines of flux is determined by the magnetomotive force and the reluctance of the material.) So the formula is:
B = Φ/A
Okay! believe it or not, we're going to tie this all together now.
Figure 5 shows a graph called a Hysteresis Loop where the vertical axis is labeled B for flux density and the horizontal axis is labeled H for field strength.
An interesting thing happens when you use an electromagnet to magnetize a ferromagnetic material: To begin with, before any current flows through the coil, there is no magnetic field strength present and so no flux density (point A). As current is applied field strength is created by the electromagnetic field set up and this causes a certain flux density to be present in the ferromagnetic material (this material could be the core of the electromagnet or adjacent but within the field). As the field strength (H) is increased eventually the flux density levels off and even though H is increased B will stay the same. (Point B) This is called flux saturation.
Now let's start to reduce the current through the coil (and hence the field intensity). The arrows in Figure 5 show that the flux density does not follow the same path back to zero. In fact, when the field strength is zero, B is still quite high. (Point C). Why would this be? Of course, you have magnetized the material and even though there is no electromagnetic force acting on it, it still retains some flux at the density shown. If we were to reverse the polarity of the current through the coil and force the field intensity to be set up in the opposite direction eventually we could bring the flux density down to zero. (Point D). Continuing on, we could eventually reach a saturated point in the other direction.
What's it all about?
We've just invented core memory! We'll be rich! All we have to do is... That's what core memory was about: thousands of tiny ferrous toroids with coils through them which would magnetize them in one direction when a pulse of current was supplied. After the power was removed they retained their magnetism. Non-volatile memory. (As long as nobody got silly with a magnet in the vicinity.)
And that's magnetism. Sort of. It actually gets pretty complex when we look at how electromagnetism is used to create electric motors because not only do we have to consider three dimensional vectors but alternating voltages, currents and phase angles come into it as well.
Maybe we'll look at it in another article.
Meanwhile, hopefully this will help understand the basic concepts without losing you in the jungle of terms. Next time we look at inductors ...
+++++++++++++++++++++++
Also see:
Understanding Electricity--Part III
adapted from: Electronics Handbook XV (1994)