IRON-CORED transformers are used between stages and almost invariably as a means of coupling the output stage to the speaker or other power-actuated device. A good transformer is a somewhat expensive component and because it costs more to design and make, the low-cost ones are generally poor. Because of this, the interstage transformer has gradually dropped out of use in these days of better amplifiers, although it is desirable with class-AB2 amplifiers, and essential for class-B amplifiers.
In the early days of the development of better reproduction, dynamic speakers were sometimes wound with high-impedance voice coils, a difficult and troublesome business. Before that, of course, electromagnetic speakers had high-impedance windings.
These high impedance types did not require an output trans former between them and the output stage but their technical limitations drove them out of use. Thus the output transformer has become an essential component in most audio installations.
The design of a suitable audio transformer is not at all a difficult matter, but the actual manufacture of a high-grade component at a reasonable price calls for a somewhat specialized production technique and it is rare for a general electronics manufacturer to "roll his own." The specialist transformer manufacturer is, there fore, the usual source of supply. He will provide exactly what the designer wants if the designer knows what he wants.
Transformer characteristics

Fig. 601. Relationship between primary and secondary windings of a transformer:
a) stepup transformer; b) stepdown transformer.
Transformers for audio frequencies are far from being ideal, simply because it is impossible to make a perfect transformer. The ideal transformer would have infinite reactance at all frequencies but zero winding resistance. The windings would have no self capacitance; there would be no leakage inductance (another way of saying that the coupling between the windings would be perfect) and there would be absolutely no losses in the core. In audio engineering the widest frequency band usually required is between 20 and 20,000 cycles, so a less-than-perfect transformer can be used quite successfully. The designer must know just what imperfections can be allowed. This involves some consideration of what the transformer has to do and how it does it.
A transformer usually has two windings, primary and secondary, but these are not always separate. A single-winding transformer with a tap in the winding is called an autotransformer. An ac voltage applied to the primary winding will be stepped up or down according to the ratio between the turns in the primary and secondary windings. If the primary winding has 1,000 turns and the secondary 2,000, then a voltage x applied to the primary will be stepped up to a voltage 2x across the secondary. If an auto transformer has a winding of 1,000 turns with a tap at 500, and if the primary voltage x is applied across the 500-turn section, the voltage across the whole winding will be 2x. But only exactly if it is an ideal transformer. See Fig. 601.
Transformer efficiency
The imperfections in a practical transformer may be lumped together and expressed as a percentage efficiency. The ideal trans former would be 100% efficient and the ratio of secondary volts to primary volts will be equal to the ratio of secondary turns to primary turns. But if the efficiency is less than 100% (and in small power transformers it may be as low as 85%), it is obvious that extra turns have to be added to the secondary winding to get the desired output voltage. How many extra turns are needed depends on the size of the core, that is, on the cross-section of that part of the core which is surrounded by the windings.
Design considerations
To make the matter simple, the case of power transformers for the 50- or 60-cycle power line, such as are used in amplifier power supplies, can be considered first. There is no basic difference be tween these and transformers for a wide range of audio frequencies but, since they have to cater only to a single low frequency, they are easier to consider and design. Current passing through the primary winding sets up a magnetic field which results in magnetic flux in the core. If too much flux is created in the core, the core will become saturated and cease to perform efficiently; iron losses will be set up. The core must therefore be adequate to carry the total power transformed without saturation of the iron; the core size determines the number of turns per volt required for the primary winding.
A useful empirical formula, applicable to most normal core shapes, gives the area of cross-section of the core (in square inches) and reads: jvA 5.58 where VA is the output in volt-amperes (assuming a working frequency of 60 hz). The number of primary turns required is obtained from the fundamental transformer equation: 108E N 4.44 £BA where N equals primary turns; f equals frequency in cycles; B equals maximum flux density and A is the area of the core cross section in square inches. E, of course, is the applied ac voltage.
From this equation it is evident that the smaller the core, the more turns are required; that is, the turns per volt rise as the core size decreases. Now there is an optimum shape of core lamination and a small core results in a small lamination with a small window to accommodate the winding. But as more turns have to be placed into the small window, the gauge of the wire for the winding must be smaller and the de resistance will rise. So power is wasted by heating the winding and the efficiency goes down. This loss of efficiency is due to copper loss (so called to distinguish it from losses due to the iron core) and must be compensated for by in creasing the number of turns on the secondary winding beyond the number that would be required by a perfect transformer.
Summarized, the considerations for a suitable design of transformer for a 50- or 60-cycle line are: the core should be of adequate size for the power transformed with due regard to the permeability and B-H of the core material; the primary turns must be properly selected for the core size required; and the secondary turns must be increased, beyond the theoretical number of turns required, to compensate for losses in the transformer.
It will be obvious that the larger the core the greater the winding space available, the heavier the gauge of wire that can be used and the smaller the copper losses. Accordingly, the larger the trans former the greater is its efficiency. Large industrial transformers are produced with an efficiency above 99%; very small ones may have an efficiency as low as 80%. As another consideration a transformer for a 25-cycle power line must have a larger core than one for 50, because more turns per volt are required to avoid saturation, and one for 100 cycles can have a smaller core. We can now consider transformers for the whole audio-frequency range.
Audio transformers are used for power transference either as interstage or output couplings. There is also the special case, at the input of an amplifier, of small transformers for impedance matching between a microphone, pickup or recording head and the first tube, but such are called upon to handle very little power.
However they introduce another problem: being used at a point which is followed by the whole gain of the amplifier, they must clearly avoid injecting any signal except that which originates in the voltage-creating device connected to them. They are susceptible to any stray interference in their field. A common type of interference is hum set up by the fields of other inductive devices such as power transformers and smoothing chokes. The input transformer must, therefore, have as small an external field as possible and must be completely shielded. A material of high permeability, such as Mu-metal, is used for the core laminations as well as the screening box into which the transformer must be fitted.
The great advantage of high-permeability core materials is that a much smaller winding is needed to secure a given inductance.
If the winding is smaller, its self-capacitance is appreciably less.
That does this mean in actual practice? An audio transformer is an impedance-matching device, its stepup and stepdown characteristics enabling different impedances to be accurately matched. In a power transformer the concern is impedance matching at one frequency and this can be translated simply into voltage alteration to suit the circuit requirements.
The audio transformer must match specified impedances at all frequencies if distortion is to be avoided. At low frequencies an insufficient primary inductance will cause a loss of voltage developed across the windings; at high frequencies the self-capacitance of the winding itself will shunt down the voltage while leakage inductance will prevent voltage being transferred from one circuit to the other. High-permeability cores will help at both ends of the frequency scale but, as high permeability cores are easily saturated, they can be used only for transformers handling small power.
If used for interstage coupling, the plate current of the pre ceding tube must be kept out of the primary winding by parallel fed connections.
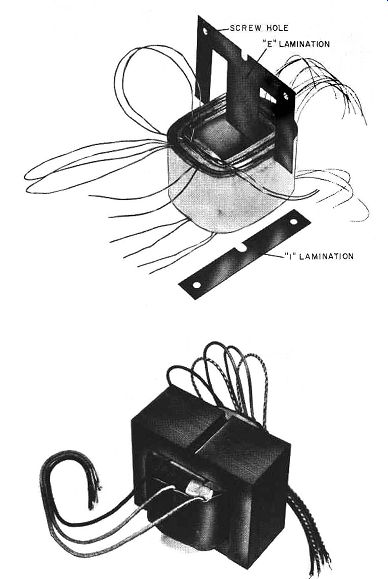
Fig. 602. Internal view of a high-quality audio output transformer:
a) single-core lamination and windings; b) assembly of complete core
and windings. (Photos courtesy Dyna Co.).
Interstage transformers Interstage transformers are also, generally, low-level trans formers. It is obviously desirable that the transformation ratio should be constant over the whole frequency range of the amplifier; without particular care being taken in the design of the transformer this will not occur.
The stepup ratio at low frequencies can be expressed by the following equation:
Stepup ratio at low frequencies = Stepup ratio at mid-frequency
... where R is the plate resistance of the previous tube, plus the primary resistance; L is the effective primary inductance and w is equal to 2 pi f. When wL = 2R, the attenuation will be 1 db; when wL = R, the attenuation will be 3 db.
At high frequencies, the reactance of the leakage inductance, the self-capacitance of the windings, and the value of R will form a low-Q resonant circuit so that the response of the transformer will peak at a frequency determined by the values of the components; beyond this resonant frequency the response will fall rapidly. The frequency of the peak can be raised by lowering the self-capacitance and leakage inductance of the windings, which can be achieved by winding in sections with primary and secondary sections interposed to give very good coupling.
As the leakage inductance is proportional to the square of the turns, the response can be extended by decreasing turns but, as the primary inductance must be maintained for good bass response, the solution is to use high-permeability core material. As compared with silicon-steel stampings, Mumetal will increase the primary inductance of the same windings over twenty times. To remove the peak from the response of the transformer, this can be done by winding with resistance wire, which lowers the Q; but if this is overdone, the response will fall off too severely.
Output transformers
These general considerations also apply to output transformers but, as these are called upon to handle quite appreciable audio power plus the steady de of an output tube or the out-of-balance de of push-pull tubes, easily saturated high-permeability cores are unsuitable and recourse has to be made to silicon steel (or one of the new types of core recently introduced). As the leakage inductance and self-capacitance of the windings normally will be considerable-added to which is the difficulty that the secondary winding has comparatively few turns-attention must be paid to the method of winding and excellence of coupling between the windings. If, moreover, the output transformer is of the multi ratio type, the coupling may not be constant over the range of tappings and the leakage inductance will therefore vary according to the tapping used for any particular secondary load. (The internal construction of a high-quality output transformer is shown in Figs. 602-a,-b.)
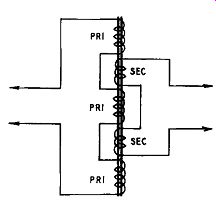
Fig. 603. Method of alternating primary and secondary windings to reduce
leak age inductance.
Given a single ratio output transformer and choice of a heavy gauge wire for the secondary winding, it is usual and convenient to split the primary into three sections with a two-section secondary sandwiched between the primary sections. This will give reason ably low leakage inductance but the self-capacitance of the primary may be fairly high, and with cons1derable potential difference between adjacent turns. See Fig. 603.
The most perfect method that has been evolved is to wind the primary in one-turn-thick discs, which are then assembled with one-turn-thick secondary discs alternately along the core, but this is a very special method of construction. In general the primary should be wound into thin "pies", and assembled on the core, interleaved by insulating discs and secondary pies. This is a very good construction but the cost of manufacture often puts it out of consideration. The average output transformer is layer wound in sections with convenient interleaving of the secondary winding.
See Fig. 604.

Fig. 604. Special method of constructing a transformer in which the
primary and secondary windings are interleaved.
The preceding paragraphs outline the things to look for in transformer construction and, as these components are generally bought from outside sources, what must be done is to check their performance on receipt. This does not imply that the transformer manufacturers supply unreliable data as to the performance of their products, but too frequently the conditions of test and measurement arc not specified in the technical data accompanying the component, or the conditions are not what the designer has in mind. It should be standard practice, therefore, to measure the performance of every transformer acquired for use.
Testing and measuring audio transformers
The first test is for ratio, and the nominal ratio is that at mid frequency. This, for high accuracy, should be done on a special type of ac bridge but a simple test is quite sufficient for all ordinary purposes. Referring to Fig. 605-a, a 1,000- hz voltage is applied to the transformer primary through an input potentiometer. If the voltage source is controllable, the potentiometer is not required. A vtvm is now connected across the primary winding and the voltage read; the meter is transferred to the secondary winding and the voltage read again. The transformation ratio is therefore the secondary reading divided by the primary reading; it is as simple as that. Remember, however, that this ratio represents voltage stepup or stepdown. Impedances vary as the square of the turns ratio, resistance and inductance being stepped up if it is a stepup transformer, capacitance being stepped down; and the reverse with a stepdown transformer.
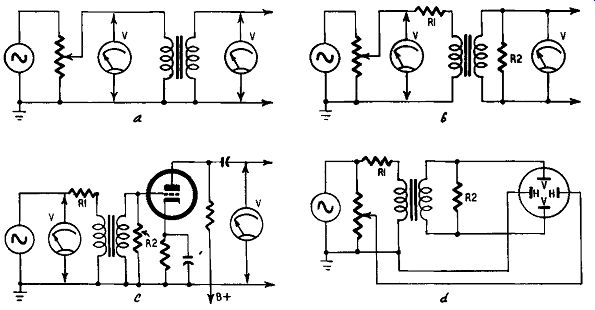
Fig. 605. Testing and measuring audio transformers: a) for turns ratio;
b) for frequency response; c) with vacuum-tube load; d) for distortion.
Testing transformer frequency response
The frequency response of an output transformer can be checked by the method of Fig. 605-b. R1 represents the internal resistance of the output tube or tubes (not the plate-to-plate load which is the load reflected on to the tubes by the secondary load multiplied by the square of the transformation ratio). R2 is the equivalent resistance of the speaker, cutter, or recording head. The input voltage is held constant in magnitude but varied from the lowest to the highest frequencies to be handled by the transformer. For each frequency the secondary voltage is read and the ratio of secondary to primary volts plotted on logarithmic paper against frequency. In this way the frequency response is determined under the working conditions that would exist were the secondary load purely resistive. If the output transformer has a multi-tapped secondary, the frequency response should be taken on each tapping.
Checking interstage transformers
An interstage transformer should be checked with the tube that will follow it, as shown in Fig. 605-c. Here R1 represents the plate resistance of the preceding tube and R2 is the grid load resistor, if used. If not used, R2 is to be omitted. Readings are taken as outlined earlier and the frequency response plotted. Naturally, in the case of both output and interstage transformers, the applied voltage should be equivalent to the peak voltage that would be applied to the transformer when actually working in the complete amplifier. As the two tests just described do not reveal distortion, if present, the next test must be for distortion under maximum working conditions.
The simple test for this is to use an oscilloscope. If a sine-wave voltage is applied to the primary, the secondary should show a sine wave on the oscilloscope. Experienced operators will detect any distortion in the trace but it is not always easy to determine whether a given trace is a sine wave. If the circuit of Fig. 605-d is used, observation of the trace is much simpler. Instead of using the internal time base of the scope, the input voltage is applied to the horizontal plates of the c-r tube, the width of trace being adjusted by the high-resistance potentiometer across the input. As before, R1 is the equivalent resistance of the preceding stage and R2 is the load resistance. If an interstage transformer is being tested and no secondary load is intended, R2 will be omitted. The secondary winding voltage is applied to the vertical plates of the c-r tube.
The trace will be a straight line at 45° if no waveform distortion is present. A good transformer will not cause distortion at high frequencies apart from treble attenuation due to leakage inductance and self-capacitance of the windings but waveform distortion can occur at low frequencies. When the core approaches saturation, the magnetizing current waveform will be far removed from a sine wave and, although the input voltage will be sinusoidal, the voltage across the primary will not. As a consequence the voltage across the secondary will have the same type of distortion but magnified by the transformation ratio. This will show up on the trace as a splitting of the center part of the straight line into a bump on either side and displaced with respect to each other. If the primary inductance is too low, the straight line will be converted into a dosed loop.
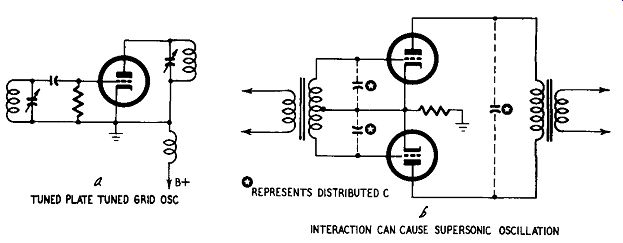
Fig. 606. The use of interstage transformers can cause parasitic oscillation.
Note the similarity between the tuned-grid tuned-plate oscillator (a)
and the push-pull output stage using an input transformer (b ).
Parasitic oscillation
Transformers can be a contributing factor to parasitic oscillation. Interelectrode capacitance in tubes setting up Miller effect can cause feedback at supersonic frequencies. A transformer in the grid circuit of an output tube has inductance and capacitance, constituting a dynamic impedance. The plate circuit also includes an inductive reactance in the shape of the output transformer and feedback will occur depending on the gain of the tube and the values in the grid and plate circuits. This can occur even when the interstage coupling is R-C, but it is more likely to happen with transformer coupling and still more likely with circuits designed for class-B amplification (Fig. 606). Presence of oscillation can be ...
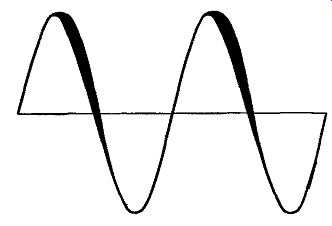
Fig. 607. Spreading of the sine wave indicates
oscillation.
... detected by a spread of the sinusoidal trace seen when the amplifier output is examined with an oscilloscope, using its internal time base in the normal manner (Fig. 607). Because Miller effect is unavoidable, class-B interstage transformers must be very carefully designed for the precise tube and circuit conditions under which they will operate and such trans formers must be tested under their normal operating conditions.
This tendency to oscillate does not imply that there is a defect in the transformer; it is merely a liability incurred by the use of transformers and resulting from tube properties. However, inter stage transformers have to be used between tubes, so the final test is that which displays the presence of supersonic oscillation. This is naturally dependent on the inductive and capacitive characteristics of the transformer.
Specification of a transformer in terms of a power-frequency response is sometimes given by the manufacturer. This is a more useful indication than a plain statement of frequency response at some predetermined small input voltage.
Detection of shorted turns, determination of leakage inductance and self-capacitance of windings, core losses and other relevant data can be determined by the regular methods described in any standard textbook on electronic procedure. It seems hardly necessary to expand this section by detailing these methods. The tests given are the most important ones from the amplifier designer's point of view and it can be assumed that responsible manufacturers avoid sending out transformers with shorted turns. Again it is not of great importance to have precise values of leakage inductance or self-capacitance; what the designer wants to know is the frequency response of the transformer under working conditions and the tests given here will tell him that.