A LOUDSPEAKER CONVERTS the electrical signal delivered to it from the amplifier to sound pressure in the listening room. Two primary parameters, therefore, are electrical input and sound pressure output . The user also wants to know how much input is required for a given output, from which can be derived the sensitivity and efficiency, also how much input can be accommodated before the loudspeaker shows signs of mechanical and/or electrical distress or severely adds to the distortion of the output . It is also useful to know the maximum output for a given level of distortion that a loudspeaker will provide.
The input impedance, and particularly how this changes over the frequency range, can be of importance from the amplifier's point of view (loudspeaker/amplifier interface) , while from the sound quality point of view we wish to know how the output changes with frequency in a controlled environment. An example loudspeaker specification is given below.
Operating principle: bass reflex
Driver units: bass dynamic 22 cm; midrange dynamic 22 cm; treble dynamic 5cm
Power handling: 50W amplifier Impedance: 8 ohms nominal (see text)
Input power for 0.025W acoustical output: 15W Voltage input for96dB SPL at 1m: 10 ·25V pink noise Frequency response: 42Hz -16kHz±3dB on axis
Distortion: see text
Operating Principle
This parameter usually signifies the nature of the acoustical loading used for the bass unit, and is probably related to the size of the enclosure. Most of the smaller book-shelf designs adopt the acoustical suspension type of enclosure loading - sometimes referred to as 'infinite baffle'. Larger floor-standing models may adopt bass reflex loading, where a critically-designed aperture or tunnel at the bottom exhausts the low bass sounds thereby helping with the output of the bass unit.
The nature of the loading has a bearing on efficiency. In general, bass reflex loud-speakers are more efficient than the smaller acoustical suspension designs . There are variations, including the acoustical labyrinth and tuned-pipe designs . The most efficient of all designs in the horn-loaded loudspeaker, which may have an efficiency as high as 20 or 30%, compared with the less than 1 % of some of the other designs . In general, the larger the loudspeaker the greater its efficiency and the better its low bass response, but it is noteworthy that low bass can only be reproduced adequately in a very large room. In the average listening room the long wavelengths of the low frequencies have insufficient space in which fully to develop.
Details of loudspeaker design and construction are given in our guides entitled Pickups and Loudspeakers and The Audio Handbook.
Drive Units
This parameter states the number and sizes of the drive units used in the design. When there are units for bass (woofer) , mid-range and treble (tweeter) the loudspeaker is sometimes called a 'three-way' design. A 'two-way' loudspeaker would thus consist of a bass unit (also handling middle frequencies) and a treble unit.
The separate units are fed with their designed-for range of frequencies from a frequency-divider network. Some designs use just one unit, called a wide-range unit; but nowadays hi-fi loudspeakers are equipped with, at least, two units . A separate unit or driver for small frequency ranges eases the distortion problems, particularly Doppler distortion, but unless correctly designed the frequency-divider can introduce problems of its own, sometimes causing undue 'coloration' and aggravating loudspeaker/amplifier interface problems.
Power Handling
This parameter indicates the power of an amplifier that can be used with the loudspeaker when the amplifier is delivering music signal . The loudspeaker would, of course, work with lower-power amplifiers but at reduced peak sound intensity. For example, a 50W rating generally means that the loudspeaker can be safely used with a 50W per channel amplifier provided that the amplifier is handling music signal . If 50W of steady-state sinewave signal were applied to the loudspeaker it might well protest, overheat and eventually fail. The average power of music signal is significantly less than the average power of steady-state signal . However, it is less well known that an amplifier of power suitable for the loudspeaker can put the loudspeaker into trouble if the amplifier is driven hard so that it is clipping badly on music signal. The power in the signal then rises so that it is getting more towards the steady-state value.
This can also apply when the amplifier's rated power is below the rated power handling of the loudspeaker. Tweeters, too, can fail if the loudspeaker is driven fairly hard from FM tuner noise which occurs between stations . This is why it is a good idea to tune with the muting active. Amplifier peak clipping is another cause of unit failure.
Impedance
Since a loudspeaker system consists of resistive as well as reactive elements (i .e. the resistance of the speech coils and the inductors of the frequency divider and the inductance and capacitance of the frequency-divider) , its impedance fails to hold constant over the frequency range. The parameter thus states a nominal value of impedance which occurs round 400Hz or, perhaps, 1kHz.
Most loudspeakers exhibit a substantial increase in impedance round the 30 to 40Hz mark, corresponding to the natural resonance of the bass unit when acoustically loaded in its enclosure. At this frequency the cone vibrates vigorously (when the loudspeaker is fed from a relatively high impedance source) and the corresponding movement of the speech coil in the magnetic field generates a back e.m.f. (electromotive force) in the coil (dynamo principle), and it is this which is responsible for the impedance rise - called 'motional impedance' . Happily, the changing impedance has less adverse effect on the reproduction than may first be thought. One reason for this is that the source impedance of a hi-fi amplifier is very low (typically between 0.2-0.1 ohm) so the loudspeaker's impedance change is 'swamped' (also see Section 2, particularly under Damping Factor), but the energy stored in the mechanical response can cause interface intermodulation distortion (IMD) in the amplifier. That is, a hi-fi amplifier can be regarded as a constant voltage source, which is partly a function of the applied negative feedback.
Nevertheless, a loudspeaker is current operated, implying that the output will fall as the impedance rises and hence the current falls. At the motional impedance frequency this is not a bad thing, anyway, since at this frequency the cone is more active and tending to produce more sound output - the reduced current thus countering the effect. At higher frequencies the designer needs to keep the inductance as small as possible and retain as constant impedance as possible.
Phase Angle
The voltage across the purely resistive elements of the complex impedance is in phase with the current; but with reactance (inductance and capacitance) , which comprises the other elements, this no longer holds true. The degree of phase lead or lag of the current with respect to the voltage is called the phase angle, which is dependent on the ratio of resistance and reactance. When the impedance is essentially reactance the phase angle will veer towards 90° and when essentially resistive the phase angle will be closer to zero degrees (in phase condition) . Now, the amount of electrical power drawn by a load is influenced by the phase angle. When the phase angle is zero degrees , as with a pure resistance, the power is equal to the voltage across the load times the current flowing through it (i.e. , VI) ; but when there is a phase angle the power drawn is equal to VI times the cosine of the phase angle (e.g., Vlcos 0) . The term cos 0 is known as the power factor, and when this is zero, as in the case when the phase angle is exactly 90° , the power drawn is zero watts ! Clearly, then, one can never be sure just how much amplifier power a loudspeaker is consuming.
Large Phase Angle Effect
Another thing which happens when the phase angle is fairly large, and the modulus of loudspeaker impedance low, is that the output transistor protection circuits of some amplifiers are prematurely activated (for example, at a particular music frequency the current may rise to a high value when the voltage has not reached its final value) . This can cause severe distortion at an amplifier power not promised by its resistive-loaded power rating. In other words, it can severely restrict the sound pressure level (SPL), even though the amplifier may be quite powerful, relative to a given amount of distortion. More information on the phenomenon is given in Section 2, under Amplifier/Loudspeaker Interface.
We make no apologies for emphasizing this aspect of amplifier/loudspeaker interface because in our judgment it is a major contribution for the different auditioning of different amplifiers when connected to different loudspeakers. Our lab has researched the problem and have discovered that certain amplifiers are more critical than others of the type of loudspeakers used with them; also, that certain loudspeakers are more difficult to partner with this type of amplifier than others (see, for example, our paper entitled Interface-Amplifier to Loudspeaker on page 87 of Hi-Fi News and Record Review, December 1976 issue) . Also see reference to IID.
Impedance Change
The curves in Fig. 6.1 show (lower) how the impedance of a loudspeaker can change over 20Hz to 20kHz (left-hand vertical scale) and the swing of phase angle over the same frequency range (upper and right-hand vertical scale) . The loudspeaker has a nominal impedance of 8-ohm, shown by the broken horizontal line, and the arrow indicates a frequency where the impedance falls below the nominal at a wide phase angle.
This might incite premature operation of the protection circuits of some amplifiers . KEF is one loudspeaker firm who has been aware of this problem for many years, and who is now testing loudspeakers for phase angle as well as impedance and, of course, frequency/pressure response -- issuing curves such as that in Fig. 6.1. Also see curves (a) and (b) in Fig. 6.2.
Input Power for 25mW Acoustical Output
When a loudspeaker is operating on special signal under hemispherical conditions in an anechoic chamber and the pickup microphone is placed lm away on axis, the acoustical output of the loudspeaker is approximately 0.025W (25m W) when the sound pressure level indicated by the microphone is 96dB or 12 microbars (uB), based on the DIN technique (see The Audio Handbook pages 19-21).
The efficiency of the loudspeaker can thus be calculated by measuring the electrical input required for this condition. If, as in the example specification, 15W are required, then the efficiency is 0.025/50 x 100, or 0.166 %, which is not untypical of a small loudspeaker of hi-fi class.
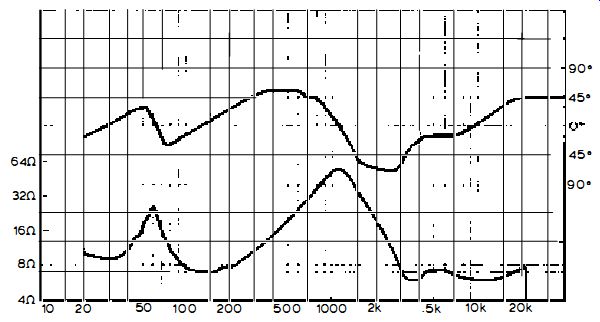
Fig. 6.1: Curves showing (top) phase angle at right-hand scale and (bottom)
impedance at left-hand scale of a loudspeaker over 20Hz -20kHz. The arrow
indicates the frequency when the modulus of impedance falls below the nominal
( indicated by the broken horizontal line) at a phase angle of about 45°.
Voltage input for 96dB Sound Pressure Again, based on the DIN technique,
the sensitivity of a loudspeaker corresponds to the input voltage of special
signal required for 96dB (12?o?b) SPL at 1m under hemispherical anechoic
conditions . This, in our judgment, is a far better way of assessing loudspeaker
sensitivity, rather than in terms of efficiency based on electrical and
acoustical powers.
We have seen that it is virtually impossible to know just how much power is being abstracted by a loudspeaker owing to its power factor. It is also much easier to tie in with amplifier output if this were given in more meaningful voltage rather than in electrical power measured across a resistive load, which is untypical of a real loudspeaker.
After all, a hi-fi amplifier is a constant voltage device and as such should be rated in output voltage obtainable across specified loads. You would then soon know whether-the amplifier would (or not) drive 'difficult' loudspeakers or jib at large phase angles when accompanied by very low real parts of the impedance!
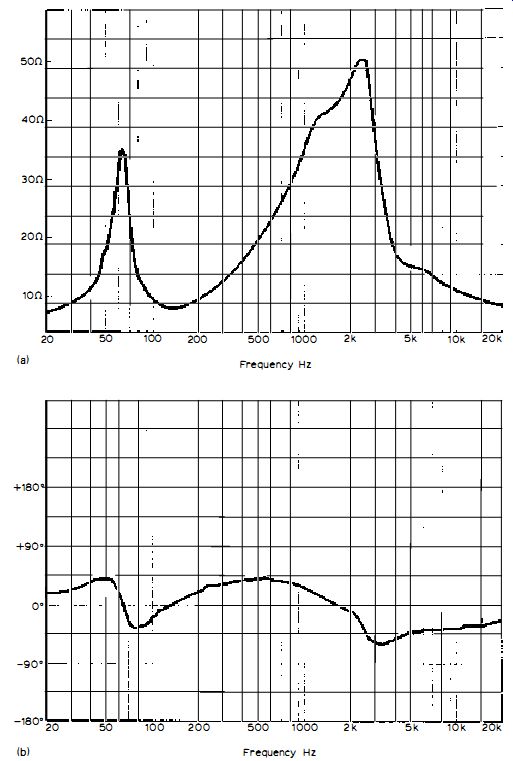
Fig. 6.2: Loudspeaker curves, showing at (a) the modulus of impedance
and at (b) the phase angle of impedance.
Frequency Response
When terminal frequency references are given, as in the example spec, one cannot tell how the sound output pressure varies with frequency. A comprehensive spec, therefore, includes, at least, one response curve taken on axis, as the upper curve in Fig. 6.3. The lower curve shows how the response changes when the loudspeaker is turned through 30° . Higher frequencies are propagated over smaller angles-than lower ones . At very low frequencies, in fact, a loudspeaker approaches an omnidirectional characteristic, which is why the off-axis curve shows more of a difference at the high-frequency end relative to the on-axis curve. A fair amount of high-frequency distribution is not undesirable, and tweeters are designed to provide for this.
Insufficient dispersion tends to reduce the area over which the best stereo effect is obtained, while excessive dispersion, leading to the totally omnidirectional loudspeaker, has the effect of reducing the definition of the stereo image, though the overall effect is not disliked by some people.
Undulations in the response characteristic influence the auditioning of loudspeakers in different ways , depending on frequency and violence of response change. The most important part of the response is from 50Hz to 15kHz and over this range the response should be as 'smooth' as possible. However, in some designs dips are deliberately arranged to occur round the middle frequencies to counteract coloration elsewhere or to yield a specific condition.
If a significant boost follows a dip some coloration is generally detected, the precise effect depending on the frequencies concerned.

Fig. 6.3: Loudspeaker frequency response curves, upper on axis and lower
30° off-axis.
Response Characteristics
Frequency response characteristics are essential during the design stages of a loudspeaker, and they reveal how well the designer has resolved the various problems of frequency-dividing, signal distribution to the various drivers, enclosure design (at the bass end) and so forth. They cannot indicate conclusively, though, how the system will audition in the real listening room, for many of the published responses are taken under anechoic conditions (i .e., in a room without reverberation). An entirely different response characteristic is achieved with the loudspeaker in the listening room, since then the sound reaching the ears is influenced by the reverberation times (at different frequencies) of the room, by the furnishings and the damping provided by these.
The curves in Fig. 6.4 refer to a pair of loudspeakers operating in an average listening room with both driven together, with the left only driven and with the right only driven. The input was noise signal and the response was plotted via a tuned third-octave filter with the sound pressure at 1kHz normalized for the different conditions . The rather violent response changes are due to resonances, a particularly bad one in the example being at 100Hz and a less violent one at 45Hz.
Distortion
Harmonic, intermodulation and Doppler distortion are often measured by the designer and, perhaps , the reviewer but are not always clearly defined in the manufacturers' specifications . The distortion rises with increase in sound output. For example, at 80Hz the 2nd and 3rd harmonic distortion of a good loudspeaker may be round 0.5% at 80dB SPL, 0.65% at 90dB and 2.5% at 100dB. At 4kHz and higher frequencies the distortion is often less, example values being 0.08% at 80dB SPL, 0.15% at 90dB and 0.2% at 100dB. Distortion sidebands (IMD) from driving signals at 500Hz and 2kHz and a composite signal SPL of 90dB may range over 0.15% to 0.3%. Most distortion is produced at low frequencies when the bass unit is driving hard.
Doppler distortion is produced when a drive unit is called upon to handle a wide range of frequencies. For example, if the bass unit is operative at , say, 2 to 3kHz as well as at lower frequencies, the high frequencies are radiated from a cone which is also vibrating vigorously at a lower frequency.
This produces a kind of 'frequency modulation', called Doppler distortion owing to the change in high-frequency with lower frequency cone motion.
Using 100Hz and 3kHz signals at a composite SPL of 90dB, Doppler distortion can range from as high as 4% down to 0.25%, depending on loudspeaker design.
It is now generally agreed, however, that hi-fi loudspeakers rarely produce sufficient Doppler distortion to be audible on music signal reproduced under normal domestic conditions . Another distortion produced by loudspeakers and currently being unfolded is 'delayed resonance' , which is shown up by impulse tests and computer analysis. The effect is that small areas of the cone tend to 'store' energy and Fig. 6.4: Frequency response curves taken with a tuned third-octave filter on noise signal of a pair of stereo loudspeakers under three conditions in an average listening room (see text for details) ... then release it after the signal responsible has vanished. It would appear that this is one of the most audible of loudspeaker distortions . This can cause the IID already mentioned.
Amplifier Power Requirement
Finally in this section, a word or two about the power requirements of the amplifier would not be amiss . A peak program sound pressure level of 96dB in the listening room is regarded by most hi-fi enthusiasts as adequate.
To secure this sort of peak SPL from a stereo system operating in an average listening room you will require a power input to each loudspeaker which is approximately 2.5 times ( +4dB) the power required by the loudspeaker for 25mW acoustical output. Thus with a pair of loudspeakers of efficiency equal to that of the example specification you will need a 40+40W amplifier.
Alternatively, you will need an amplifier capable of providing 4dB (1.585 times) more voltage per channel than the voltage input required by the loudspeaker for 96dB SPL at lm under hemispherical anechoic conditions. Based on the loudspeaker of the example spec again, this means that you will need an amplifier capable of providing 16-25V to each loudspeaker without clipping or distorting.
= = = =