Digital Audio: Sound quality considerations (part 1)

.

• 1 Introduction
• 2 Information capacity
• 3 Loudspeaker problems
• 4 Subjective and objective testing
• 5 Objective testing
• 6 Subjective testing
• 7 Digital audio quality
• 8 Use of high sampling rates
• 9 Digital audio interface quality
• 10 Compression in stereo

Sound reproduction can only achieve the highest quality if every step is carried out to an adequate standard. This requires a knowledge of what the standards are and the means to test whether they are being met, as well as some understanding of psychology and a degree of tolerance!

1. Introduction

In principle, quality can be lost almost anywhere in the audio chain whether by poor interconnections, the correct use of poorly designed equipment or incorrect use of good equipment. The best results will only be obtained when good equipment is used and connected correctly and frequently tested or monitored.

FIG. 1 shows a representative digital audio system which contains all the components needed to go from original sound to reproduced sound. Like any chain, the system is only as good as its weakest link. It should be clear that a significant number of analog stages remain, especially in the area of the transducers. There is nothing fundamentally wrong with analog equipment, provided that it’s engineered to the appropriate quality level. It’s regrettable that the enormous advance in signal performance which digital techniques have brought to recording, processing and delivery have largely not been paralleled by advances in subjective or objective testing.

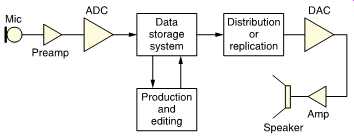
FIG. 1 The major processes in a digital audio system. Quality can be lost anywhere and can only be assessed by considering every stage.

FIG. 2 The hearing system is part of the mind's mechanism for modeling its surroundings and it works in time, space and frequency. The traditional fixation with the frequency domain leads to neglect of or damage to the other two domains.

FIG. 3 Some quality considerations. At (a) an incomplete list of criteria that must be met for accurate reproduction. At (b) in a real-world system, the criteria of (a) must be met in all the components in the chain. The monitoring system should be at least as good as the best anticipated consumer reproduction system. (c) an ideal system has ideally equal performance in all stages. Real system at (d) has better performance in signal processing than in transducers. Excess performance is a waste of money.

It ought to be possible, even straightforward, to monitor every stage of FIG. 1 to see if its performance is adequate. If adequate stages are retained and inadequate stages are improved, the entire system can be improved. In practice this is not as easy as it seems. As will be seen in this section, the audio industry has not established standards by which the entire system of FIG. 1 can be objectively measured in a way which relates to what it will sound like. The measurements techniques which exist are incomplete and the criteria to be met are not established.

FIG. 2 shows that the human hearing system operates in three domains; time, frequency and space. In real life we know where a sound source is, when it made a sound and the timbral character of the sound.

If a high-quality reproduction is to be achieved, it’s necessary to test the equipment in all these domains to ensure that it meets or exceeds the accuracy of the human ear. The frequency domain is reasonably well served, but the time and space domains are still suffering serious neglect.

The ultimate criterion for sound reproduction is that the human ear is fooled by the overall system into thinking it has heard the real thing. It follows that even to approach that ideal, the properties of human hearing have to form the basis for design judgments of every part of the audio chain. It’s generally assumed that the more accurate some aspect of a reproduction system is, the more realistic it will sound, but this doesn't follow. In practice this assumption is only true if the accuracy is less than the accuracy of the hearing system. Once some aspect of an audio system exceeds the accuracy of the hearing system, further improvement is not only unnecessary, but it diverts effort away from other areas where it could be more useful.

FIG. 3(a) shows some criteria by which audio accuracy can be assessed. In each area, it should be possible to measure the requirements of the listener using whatever units are appropriate in order to create a multi-criterion threshold. FIG. 3(b) shows that these criteria must be met equally despite the sum of all degradations in every stage of the audio chain from microphone to speaker. FIG. 3(c) shows that a balance must be reached in two dimensions so that each criterion is given equal attention in every stage through which the signal passes. This gives the best value for money whatever standard is achieved. Figure (d) shows a more common approach which is where the excess quality of some parts of the system is wasted because other weak parts dominate the impression of the listener. The most commonly found error is that the electronic aspects of audio systems are overspecified whilst the transducers are underspecified.

2 Information capacity

The descriptions of time, frequency and space carried in an audio system represent information, and an analysis of audio system quality falls within the scope of information theory. In the digital domain, the information rate is fixed by the wordlength and the sampling rate. The wordlength determines how many different conditions can be described by each sample. For example a sixteen-bit sample can have 65 536 different values.

In order to reach this performance, every item in the chain needs to have the same information capacity. Recent ADCs and DACs approach this performance, but transducers in general and loudspeakers in particular don't.

Any audio device, analog or digital, can be modeled as an information channel of finite capacity whose equivalent bit rate can be measured or calculated. This can also be done with the loudspeaker. This equivalent bit rate relates to the realism which the speaker can achieve.

When the speaker information capacity is limited, the presence of an earlier restriction in the signal being monitored may go unheard and it may erroneously be assumed that the signal is ideal when in fact it’s not.

3 Loudspeaker problems

The use of poor loudspeakers simply enables other poor audio devices to enter service. When most loudspeakers have such poor information capacity, how can they be used to assess this capacity in earlier components in the audio chain? ADCs, DACs, pre- and power amplifiers and compression codecs can only meaningfully be assessed on speakers of adequate information capacity. It also follows that the definition of a high-quality speaker is one which readily reveals compression artifacts.

Non-ideal loudspeakers act like compressors in that the distortions, delayed resonances and delayed reradiation they create conceal or mask information in the original audio signal. If a real compressor is tested with non-ideal loudspeakers certain deficiencies of the compressor won’t be heard. Others, notably the late Michael Gerzon, have correctly suggested that compression artifacts which are inaudible in mono may be audible in stereo. The spatial compression of non-ideal stereo loud speakers conceals real spatial compression artifacts.

The ear is a lossy device because it exhibits masking. Not all the presented sound is sensed. If a lossy loudspeaker is designed to a high standard, the losses may be contained to areas which are masked by the ear and then that loudspeaker would be judged transparent. Douglas Self has introduced the term 'blameless' for a device whose imperfections are undetectable; an approach which commands respect. However, the majority of legacy loudspeakers are not in this category. Audible defects are introduced into the reproduced sound in frequency, time and spatial domains, giving the loudspeaker a kind of character which is best described as a signature or footprint.

4 Subjective and objective testing

An audio waveform is simply a voltage changing with time within a limited spectrum, and a digital audio waveform is simply a number changing its value at the sampling rate. As a result any error introduced by a given device can in principle be extracted and analyzed. If this approach is used during the design process the performance of any unit can be refined until the error is inaudible.

Naturally the determination of what is meant by inaudible has to be done carefully using valid psychoacoustic experiments. Using such subjective results it’s possible to design objective tests which will measure different aspects of the signal to determine if it’s acceptable.

With care and precision loudspeakers it’s equally valid to use listening tests where the reproduced sound is compared with that of other audio systems or of live performances. In fact the combination of careful listening tests with objective technical measurements is the only way to achieve outstanding results. The reason is that the ear can be thought of as making all tests simultaneously. If any aspect of the system has been overlooked the ear will detect it. Then objective tests can be made to find the deficiency the ear detected and remedy it.

If two pieces of equipment consistently measure the same but sound different, the measurement technique must be inadequate. In general, the audio industry survives on inadequate measurement in the misguided belief that the ear has some mysterious power to detect things that can never be measured.

A further difficulty in practice is that the ideal combination of subjective and objective testing is not achieved as often as might be thought. Unfortunately the audio industry represents one of the few remaining opportunities to find employment without qualifications.

Given the combination of advanced technologies and marginal technical knowledge, it should be no surprise that the audio industry periodically produces theories which are at variance with scientific knowledge.

People tend to be divided into two camps where audio quality is concerned.

Subjectivists are those who listen at length to both live and recorded music and can detect quite small defects in audio systems. Unfortunately most subjectivists have little technical knowledge and are quite unable to convert their detection of a problem into a solution. Although their perception of a problem may be genuine, their hypothesis or proposed solution may require the laws of physics to be altered. A particular problem with subjective testing is the avoidance of bias. Technical knowledge is essential to understand the importance of experimental design. Good experimental design is important to ensure that only the parameter to be investigated changes so that any difference in the result can only be due to the change. If something else is unwittingly changed the experiment is void. It’s also important to avoiding bias. Statistical analysis is essential to determine the significance of the results, i.e. the degree of confidence that the results are not due to chance alone. As most subjectivists lack such technical knowledge it’s hardly surprising that a lot of deeply held convictions about audio are simply due to unwitting bias where repeatable results are simply not obtained.

A classic example of bias is the understandable tendency of the enthusiast who has just spent a lot of money on a device which has no audible effect whatsoever to 'hear' an improvement.

Another problem with subjectivism is caused by those who don't regularly listen to live music. They become imprinted on the equipment they normally use and subconsciously regard it as 'correct'. Any other equipment to which they are exposed will automatically be judged incorrect, even if it’s technically superior. On the introduction of FM radio, with 15 kHz bandwidth, broadcasters received complaints that the audio was too shrill or bright. In comparison with the 7 kHz of AM radio it was! The author loaned an experimental loudspeaker with a ruler-flat frequency response to an experienced sound engineer. It was returned with the complaint that the response had a peak. The engineer even estimated the frequency of the peak. It was precisely at the crossover frequency of the speakers he normally uses, which have a notorious dip in power response.

It’s extremely difficult to make progress when experienced people acting in good faith make statements which are completely incorrect, but exposure to the audio industry will show that this is surprisingly common.

Objectivists are those who make a series of measurements and then pronounce a system to have no audible defect. They frequently have little experience of live performance or critical listening. One of the most frequent mistakes made by objectivists is to assume that because a piece of equipment passes a given test under certain conditions then it’s ideal.

This is simply untrue for several reasons. The criteria by which the equipment is considered to pass or fail may be incorrect or inappropriate.

The equipment might fail other tests or the same test under other conditions. In some cases the tests which equipment might fail have yet to be designed.

Not surprisingly, the same piece of equipment can be received quite differently by the two camps. The introduction of transistor audio amplifiers caused an unfortunate and audible step backwards in audio quality. The problem was that vacuum-tube amplifiers were generally operated in Class A and had low distortion except when delivering maximum power. Consequently valve amplifiers were tested for distortion at maximum power and in a triumph of tradition over reason transistor amplifiers were initially tested in the same way. However, transistor amplifiers generally work in Class B and produce more distortion at very low levels due to crossover between output devices.

Naturally this distortion was not detectable on a high-power distortion test. Early transistor amplifiers sounded dreadful at low level and it’s astonishing that this was not detected before they reached the market when the subjectivists rightly gave them a hard time.

Whilst the objectivists looked foolish over the crossover distortion issue, subjectivists have no reason to crow with their fetishes for gold plated AC power plugs, special feet for equipment, exotic cables and mysterious substances to be applied to Compact Discs.

The only solution to the subjectivist/objectivist schism is to arrange them in pairs and bang their heads together.

FIG. 4 All waveform errors can be broken down into two classes: those due to distortions of the signal and those due to an unwanted additional signal.

5 Objective testing

Objective testing consists of making measurements which indicate the accuracy to which audio signals are being reproduced. When the measurements are standardized and repeatable they do form a basis for comparison even if per se they don’t give a complete picture of what a device-under-test (DUT) or system will sound like.

There is only one symptom of quality loss which is where the reproduced waveform differs from the original. For convenience the differences are often categorized.

Any error in an audio waveform can be considered as an unwanted signal which has been linearly added to the wanted signal. FIG. 4 shows that there are only two classes of waveform error. The first is where the error is not a function of the audio signal, but results from some uncorrelated process. This is the definition of noise. The second is where the error is a direct function of the audio signal which is the definition of distortion.

FIG. 5 (a) SNR is the ratio of the largest undistorted signal to the noise floor. (b) Maximum SNR is not reached if the signal never exercises the highest possible levels.

Noise can be broken into categories according to its characteristics.

Noise due to thermal and electronic effects in components or analog tape hiss has essentially stationary statistics and forms a constant background which is subjectively benign in comparison with most other errors. Noise can be periodic or impulsive. Power frequency-related hum is often rich in harmonics. Interference due to electrical switching or lightning is generally impulsive. Crosstalk from other signals is also noise in that it does not correlate with the wanted signal. An exception is crosstalk between the signals in stereo or surround systems.

Distortion is a signal-dependent error and has two main categories.

Non-linear distortion arises because the transfer function is not straight.

The result in analog parts of audio systems is harmonic distortion where new frequencies which are integer multiples of the signal frequency are added, changing the spectrum of the signal. In digital parts of systems non-linearity can also result in anharmonic distortion because harmonics above half the sampling rate will alias. Non-linear distortions are subjectively the least acceptable as the resulting harmonics are frequently not masked, especially on pure tones.

Linear distortion is a signal-dependent error in which different frequencies propagate at different speeds due to lack of phase linearity. In complex signals this has the effect of altering the waveform but without changing the spectrum. As no harmonics are produced, this form of distortion is more benign than non-linear distortion. Whilst a completely linear phase system is ideal, the finite phase accuracy of the ear means that in practice a minimum phase system is probably good enough.

Minimum phase implies that phase error changes smoothly and continuously over the audio band without any sudden discontinuities.

Loudspeakers often fail to achieve minimum phase, with legacy techniques such as reflex tuning and passive crossovers being particularly unsatisfactory.

FIG. 5(a) shows that the signal-to-noise ratio (SNR) is the ratio in dB between the largest amplitude undistorted signal the DUT can pass and the amplitude of the output with no input whatsoever, which is presumed to be due to noise. The spectrum of the noise is as important as the level. When audio signals are present, auditory masking occurs which reduces the audibility of the noise. Consequently the noise floor is most significant during extremely quiet passages or in pauses. Under these conditions the threshold of hearing is extremely dependent on frequency.

A measurement which more closely resembles the effect of noise on the listener is the use of an A-weighting filter prior to the noise level measurement stage. The result is then measured in dB(A).

Just because a DUT measures a given number of dB of SNR does not guarantee that SNR will be obtained in use. The measured SNR is only obtained when the DUT is used with signals of the correct level. FIG. 5(b) shows that if the DUT is installed in a system where the input level is too low, the SNR of the output will be impaired. Consequently in any system where this is likely to happen the SNR of the equipment must exceed the required output SNR by the amount by which the input level is too low. This is the reason why quality mixing consoles offer apparently phenomenal SNRs.

Often the operating level is deliberately set low to provide headroom so that occasional transients are undistorted. The art of quality audio production lies in setting the level to the best compromise between elevating the noise floor and increasing the occurrences of clipping.

Another area in which conventional SNR measurements are meaningless is where gain ranging or floating point coding is used. With no signal the system switches to a different gain range and an apparently high SNR is measured which does not correspond to the subjective result.

FIG. 6 (a) Frequency response measuring system. (b) Two devices in series have narrower bandwidth. (c) Typical record production signal chain, showing potential severity of generation loss.

The frequency response of audio equipment is measured by the system shown in FIG. 6(a). The same level is input at a range of frequencies and the output level is measured. The end of the frequency range is considered to have been reached where the output level has fallen by 3 dB with respect to the maximum level. The correct way of expressing this measurement is:

Frequency response: -3 dB, 20Hz - 20 kHz or similar. If the level limit is omitted, as it often is, the figures are meaningless.

There is a seemingly endless debate about how much bandwidth is necessary in analog audio and what sampling rate is needed in digital audio. There is no one right answer as will be seen. In analog systems, there is generation loss. FIG. 6(b) shows that two identical DUTs in series will cause a loss of 6 dB at the frequency limits. Depending on the shape of the roll-off, the -3 dB limit will be reached over a narrower frequency range. Conversely if the original bandwidth is to be maintained, then the -3 dB range of each DUT must be wider.

In analog production systems, the number of different devices an audio signal must pass through is quite large. FIG. 6(c) shows the signal chain of a multi-track-produced vinyl disk. The number of stages involved mean that if each stage has a seemingly respectable -3 dB, 20Hz- 20 kHz response, the overall result will be dreadful with a phenomenal rate of roll-off at the band edge. The only solution is that each item in the chain has to have wider bandwidth making it considerably overspecified in a single-generation application.

Another factor is phase response. At the -3 dB point of a DUT, if the response is limited by a first-order filtering effect, the phase will have shifted by 45°. Clearly in a multi-stage system these phase shifts will add.

An eight-stage system, not at all unlikely, will give a complete phase rotation as the band-edge is approached. The phase error begins a long way before the -3 dB point, preventing the system from displaying even a minimum phase characteristic.

Consequently in complex analog audio systems each stage must be enormously overspecified in order to give good results after generation loss. It’s not unknown for mixing consoles to respond down to 6Hz in order to prevent loss of minimum phase in the audible band. Obviously such an extended frequency response on its own is quite inaudible, but when cascaded with other stages, the overall result will be audible.

In the digital domain there is no generation loss if the numerical values of the samples are not altered. Consequently digital data can be copied from one tape to another, or to a Compact Disc without any quality loss whatsoever. Simple digital manipulations, such as level control, don’t impair the frequency or phase response and, if well engineered, the only loss will be a slight increase in the noise floor. Consequently digital systems don’t need overspecified bandwidth. The bandwidth needs only to be sufficient for the application because there is nothing to impair it. However, those brought up on the analog tradition of overspecified bandwidth find this hard to believe.

In a digital system the bandwidth and phase response is defined at the anti-aliasing filter in the ADC. Early anti-aliasing filters had such dreadful phase response that the aliasing might have been preferable, but this has been overcome in modern oversampled convertors which can be highly phase-linear.

FIG. 7 Squarewave testing gives a good insight into audio performance. (a) Poor low-frequency response causing droop. (b) Poor high-frequency response with poor phase linearity. (c) Phase-linear bandwidth limited system. (d) Asymmetrical ringing shows lack of phase linearity.

FIG. 8 (a) Non-linear transfer function allows large low-frequency signal to modulate small high-frequency signal. (b) Harmonic distortion test using notch to remove fundamental measures THD + N. (c) Intermodulation test measuring depth of modulation of high frequency by low-frequency signal. (d) Intermodulation test using a pair of tones and measuring the level of the difference frequency. (e) Complex test using intermodulation between harmonics. (f) Spectrum analyzer output with two-tone input.

One simple but good way of checking frequency response and phase linearity is squarewave testing. A squarewave contains indefinite harmonics of a known amplitude and phase relationship. If a squarewave is input to an audio DUT, the characteristics can be assessed almost instantly. FIG. 7 shows some of the defects which can be isolated. (a) shows inadequate low-frequency response causing the horizontal sections of the waveform to droop. (b) shows poor high-frequency response in conjunction with poor phase linearity which turns the edges into exponential curves. (c) shows a phase-linear system of finite bandwidth, e.g. a good anti-aliasing filter. Note that the transitions are symmetrical with equal pre- and post-ringing. This is one definition of phase linearity. (d) shows a system with wide bandwidth but poor HF phase response.

Note the asymmetrical ringing.

One still hears from time to time that squarewave testing is illogical because square waves never occur in real life. The explanation is simple.

Few would argue that any sine wave should come out of a DUT with the same amplitude and no phase shift. A linear audio system ought to be able to pass any number of superimposed signals simultaneously. A squarewave is simply one combination of such superimposed sine waves.

Consequently if an audio system cannot pass a squarewave as shown in FIG. 7(c) then it will cause a problem with real audio.

As linearity is extremely important in audio, relevant objective linearity testing is vital. Real sound consists of many different contributions from different sources which all superimpose in the sound waveform reaching the ear. If an audio system is not capable of carrying an indefinite number of superimposed sounds without interaction then it will cause an audible impairment. Interaction between a single waveform and a non-linear system causes distortion. Interaction between waveforms in a non-linear system is called intermodulation distortion (IMD) whose origin is shown in FIG. 8(a). As the transfer function is not straight, the low-frequency signal has the effect of moving the high-frequency signal to parts of the transfer function where the slope differs. This results in the high frequency being amplitude modulated by the low. The amplitude modulation will also produce sidebands. Clearly a system which is perfectly linear will be free of both types of distortion.

FIG. 8(b) shows a simple harmonic distortion test. A low distortion oscillator is used to inject a clean sine wave into the DUT. The output passes through a switchable sharp 'notch' filter which rejects the fundamental frequency. With the filter bypassed, an AC voltmeter is calibrated to 100 percent. With the filter in circuit, any remaining output must be harmonic distortion or noise and the measured voltage is expressed as a percentage of the calibration voltage. The correct way of expressing the result is as follows:

THD + N at 1 kHz = 0.1% or similar. A stringent test would repeat the test at a range of frequencies.

There is not much point in conducting THD + N tests at high frequencies as the harmonics will be beyond the audible range.

The THD + N measurement is not particularly useful in high-quality audio because it only measures the amount of distortion and tells nothing about its distribution. A vacuum-tube amplifier displaying 0.1 percent distortion may sound very good indeed, whereas a transistor amplifier or a DAC with the same distortion figure will sound awful. This is because the vacuum-tube amplifier produces primarily low-order harmonics, which some listeners even find pleasing, whereas transistor amplifiers and digital devices can produce higher-order harmonics, which are unpleasant.

FIG. 9 Signal resolution. At (a) an ideal signal path should output a sinewave as a single frequency. Low-resolution signal paths produce sidebands around the signal (b).

In (c), amplifiers which linearize their output using negative feedback do so by forcing the distortion into the power rails. Poor layout can couple the power rails back into the signal path.

Very high-quality audio equipment has a characteristic whereby the equipment itself seems to recede, leaving only the sound. This will only happen when the entire reproduction chain is sufficiently free of any characteristic footprint which it impresses on the sound. The term resolution is used to describe this ability. Audio equipment which offers high resolution appears to be free of distortion products which are simply not measured by THD + N tests. FIG. 9(a) shows the spectrum of a sine wave emerging from an ideal audio system. FIG. 9(b) shows the spectrum of a low-resolution signal. Note the presence of sidebands around the original signal. Analog tape displays this characteristic, which is known as modulation noise. The Compact Cassette is notorious for a high level of modulation noise and poor resolution.

Analog circuitry can have the same characteristic. FIG. 9(c) shows that signal or power amplifiers using negative feedback to linearize the output do so by pushing the non-linearities into the power rails. If the circuit board layout is poor, the power rail distortion can enter the signal path through common impedances.

In Section 4 the subject of sampling clock jitter was introduced. The effect of sampling clock jitter is to produce sidebands of the kind shown in FIG. 9(b). This will be considered further in section 13.7.

Few people realize that loudspeakers can also display the effect of FIG. 9(b). Traditional loudspeakers use ferrite magnets for economy.

However, ferrite is an insulator and so there is nothing to stop the magnetic field moving within the magnet due to the Newtonian reaction to the coil drive force. FIG. 10(a) shows that when the coil is quiescent, the lines of flux are symmetrically disposed about the coil turns, but when coil current flows, as in (b), the flux must be distorted in order to create a thrust. In magnetic materials the magnetic field can only move by the motion of domain walls and this is a non-linear process. The result in a conductive magnet is flux modulation and Barkhausen noise.

The flux modulation and noise make the transfer function of the transducer non-linear and result in intermodulation.

The author did not initially believe the results of estimates of the magnitude of the problem, which showed that ferrite magnets cannot reach the sixteen-bit resolution of CD. Consequently two designs of tweeter were built, identical except for the magnet. The one with the conductive neodymium magnet has audibly higher resolution, approaching that of an electrostatic transducer, which, of course, has no magnet at all.

Given the damaging effect on realism caused by sidebands, a more meaningful approach than THD + N testing is to test for intermodulation distortion. There are a number of ways of conducting intermodulation tests, and, of course, anyone who understands the process can design a test from first principles. An early method standardized by the SMPTE was to exploit the amplitude modulation effect in two widely spaced frequencies, typically 70Hz with 7 kHz added at one tenth the amplitude. 70Hz is chosen because it’s above the hum due to 50 or 60Hz power. FIG. 8(c) shows that the measurement is made by passing the 7 kHz region through a bandpass filter and recovering the depth of amplitude modulation with a demodulator.

FIG. 10 (a) Flux in gap with no coil current. (b) Distortion of flux needed to create drive force.

A more stringent test for the creation of sidebands is where two high frequencies with a small frequency difference are linearly added and used as the input to the DUT. For example, 19 and 20 kHz will produce a 1 kHz difference or beat frequency if there is non-linearity as shown in FIG. 8(d). With such a large difference between the input and the beat frequency it’s easy to produce a 1 kHz bandpass filter which rejects the inputs. The filter output is a measure of IMD. With a suitable generator, the input frequencies can be swept or stepped with a constant 1 kHz spacing.

More advanced tests exploit not just the beats between the fundamentals, but also those involving the harmonics. In one proposal, shown in FIG. 8(e) input tones of 8 and 11.95 kHz are used. The fundamentals produce a beat of 3.95 kHz, but the second harmonic of 8 kHz is 16 kHz which produces a beat of 4.05 kHz. This will inter modulate with 3.95 kHz to produce a 100Hz component which can be measured. Clearly this test will only work in 60Hz power regions, and the exact frequencies would need modifying in 50Hz regions.

If a precise spectrum analyzer is available, all the above tests can be performed simultaneously. FIG. 8(f) shows the results of a spectrum analysis of a DUT supplied with two test tones. Clearly it’s possible to test with three simultaneous tones or more. Some audio devices, particularly power amplifiers, ADCs and DACs, are relatively benign under steady-state testing with simple signals, but reveal their true colors with a more complex input. (cont. part 2)

. ===