17. Multiplexing principles
Multiplexing is used where several signals are to be transmitted down the same channel. The channel bit rate must be the same as or greater than the sum of the source bit rates. FIG. 32 shows that when multiplexing is used, the data from each source have to be time compressed. This is done by buffering source data in a memory at the multiplexer. They are written into the memory in real time as they arrive, but will be read from the memory with a clock which has a much higher rate. This means that the readout occurs in a smaller timespan. If, for example, the clock frequency is raised by a factor of ten, the data for a given signal will be transmitted in a tenth of the normal time, leaving time in the multiplex for nine more such signals.
In the demultiplexer another buffer memory will be required. Only the data for the selected signal will be written into this memory at the bit rate of the multiplex. When the memory is read at the correct speed, the data will emerge with its original timebase.
In practice it is essential to have mechanisms to identify the separate signals to prevent them being mixed up and to convey the original signal clock frequency to the demultiplexer. In time-division multiplexing the timebase of the transmission is broken into equal slots, one for each signal. This makes it easy for the demultiplexer, but forces a rigid structure on all the signals such that they must all be locked to one another and have an unchanging bit rate. Packet multiplexing overcomes these limitations.

FIG. 32 Multiplexing requires time compression on each input.

FIG. 33 Packet multiplexing relies on headers to identify the packets.
18. Packets
The multiplexer must switch between different time-compressed signals to create the bitstream and this is much easier to organize if each signal is in the form of data packets of constant size. FIG. 33 shows a packet multiplexing system.
Each packet consists of two components: the header, which identifies the packet, and the payload, which is the data to be transmitted. The header will contain at least an identification code (ID) which is unique for each signal in the multiplex. The demultiplexer checks the ID codes of all incoming packets and discards those which do not have the wanted ID.
In complex systems it is common to have a mechanism to check that packets are not lost or repeated. This is the purpose of the packet continuity count which is carried in the header. For packets carrying the same ID, the count should increase by one from one packet to the next.
Upon reaching the maximum binary value, the count overflows and recommences.
19. Statistical multiplexing
Packet multiplexing has advantages over time-division multiplexing because it does not set the bit rate of each signal. A demultiplexer simply checks packet IDs and selects all packets with the wanted code. It will do this however frequently such packets arrive. Consequently it is practicable to have variable bit rate signals in a packet multiplex. The multiplexer has to ensure that the total bit rate does not exceed the rate of the channel, but that rate can be allocated arbitrarily between the various signals.
As a practical matter is is usually necessary to keep the bit rate of the multiplex constant. With variable rate inputs this is done by creating null packets which are generally called stuffing or packing. The headers of these packets contain an unique ID which the demultiplexer does not recognize and so these packets are discarded on arrival.
In an MPEG environment, statistical multiplexing can be extremely useful because it allows for the varying difficulty of real program material. In a multiplex of several television programs, it is unlikely that all the programs will encounter difficult material simultaneously. When one program encounters a detailed scene or frequent cuts which are hard to compress, more data rate can be allocated at the allowable expense of the remaining programs which are handling easy material.
20. Filters
Filtering is inseparable from digital audio. Analog or digital filters, and sometimes both, are required in ADCs, DACs, in the data channels of digital recorders and transmission systems and in sampling rate convertors and equalizers. Optical systems used in disk recorders also act as filters.

FIG. 34 Group delay time-displaces signals as a function of frequency.
There are many parallels between analog, digital and optical filters, which this section treats as a common subject. The main difference between analog and digital filters is that in the digital domain very complex architectures can be constructed at low cost in LSI and that arithmetic calculations are not subject to component tolerance or drift.
Filtering may modify the frequency response of a system, and/or the phase response. Every combination of frequency and phase response determines the impulse response in the time domain. FIG. 34 shows that impulse response testing tells a great deal about a filter. In a perfect filter, all frequencies should experience the same time delay. If some groups of frequencies experience a different delay from others, there is a group-delay error. As an impulse contains an infinite spectrum, a filter suffering from group-delay error will separate the different frequencies of an impulse along the time axis.

FIG. 35 (a) The impulse response of a simple RC network is an exponential
decay. This can be used to calculate the response to a squarewave, as in (b).
A pure delay will cause a phase shift proportional to frequency, and a filter with this characteristic is said to be phase-linear. The impulse response of a phase-linear filter is symmetrical. If a filter suffers from group-delay error it cannot be phase-linear. It is almost impossible to make a perfectly phase-linear analog filter, and many filters have a group delay equalization stage following them which is often as complex as the filter itself. In the digital domain it is straightforward to make a phase linear filter, and phase equalization becomes unnecessary.
Because of the sampled nature of the signal, whatever the response at low frequencies may be, all digital channels (and sampled analog channels) act as low-pass filters cutting off at the Nyquist limit, or half the sampling frequency.
FIG. 35(a) shows a simple RC network and its impulse response.
This is the familiar exponential decay due to the capacitor discharging through the resistor (in series with the source impedance which is assumed here to be negligible). The figure also shows the response to a squarewave at (b). These responses can be calculated because the inputs involved are relatively simple. When the input waveform and the impulse response are complex functions, this approach becomes almost impossible.

FIG. 36 In the convolution of two continuous signals (the impulse response
with the input), the impulse must be time reversed or mirrored. This is necessary
because the impulse will be moved from left to right, and mirroring gives the
impulse the correct time-domain response when it is moved past a fixed point.
As the impulse response slides continuously through the input waveform, the
area where the two overlap determines the instantaneous output amplitude. This
is shown for five different times by the crosses on the output waveform.

FIG. 37 In time discrete convolution, the mirrored impulse response is stepped
through the input one sample period at a time. At each step, the sum of the
cross-products is used to form an output value. As the input in this example
is a constant-height pulse, the output is simply proportional to the sum of
the coincident impulse response samples. This figure should be compared with
FIG. 36.
In any filter, the time domain output waveform represents the convolution of the impulse response with the input waveform. Convolution can be followed by reference to a graphic example in FIG. 36.
Where the impulse response is asymmetrical, the decaying tail occurs after the input. As a result it is necessary to reverse the impulse response in time so that it is mirrored prior to sweeping it through the input waveform. The output voltage is proportional to the shaded area shown where the two impulses overlap.
The same process can be performed in the sampled, or discrete time domain as shown in FIG. 37. The impulse and the input are now a set of discrete samples which clearly must have the same sample spacing.
The impulse response only has value where impulses coincide. Elsewhere it is zero. The impulse response is therefore stepped through the input one sample period at a time. At each step, the area is still proportional to the output, but as the time steps are of uniform width, the area is proportional to the impulse height and so the output is obtained by adding up the lengths of overlap. In mathematical terms, the output samples represent the convolution of the input and the impulse response by summing the coincident cross-products.
As a digital filter works in this way, perhaps it is not a filter at all, but just a mathematical simulation of an analog filter. This approach is quite useful in visualizing what a digital filter does.
21. Transforms
FIG. 38 shows that if a signal with a spectrum or frequency content a is passed through a filter with a frequency response b the result will be an output spectrum which is simply the product of the two. If the frequency responses are drawn on logarithmic scales (i.e. calibrated in dB) the two can be simply added because the addition of logs is the same as multiplication. Whilst frequency in audio has traditionally meant temporal frequency measured in Hertz, frequency in optics can also be spatial and measured in lines per millimeter (mm-1 ). Multiplying the spectra of the responses is a much simpler process than convolution.
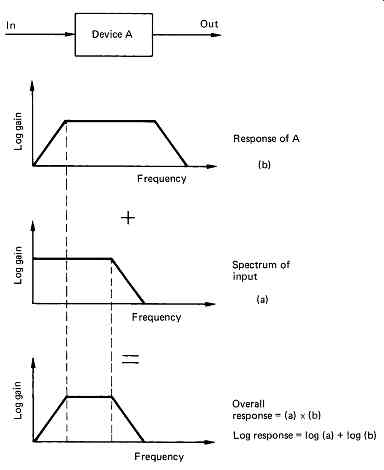
FIG. 38 In the frequency domain, the response of two series devices is the product
of their individual responses at each frequency. On a logarithmic scale the
responses are simply added.
In order to move to the frequency domain or spectrum from the time domain or waveform, it is necessary to use the Fourier transform, or in sampled systems, the discrete Fourier transform (DFT). Fourier analysis holds that any periodic waveform can be reproduced by adding together an arbitrary number of harmonically related sinusoids of various amplitudes and phases. FIG. 39 shows how a squarewave can be built up of harmonics. The spectrum can be drawn by plotting the amplitude of the harmonics against frequency. It will be seen that this gives a spectrum which is a decaying wave. It passes through zero at all even multiples of the fundamental. The shape of the spectrum is a sinx/x curve. If a squarewave has a sinx/x spectrum, it follows that a filter with a rectangular impulse response will have a sinx/x spectrum.
A low-pass filter has a rectangular spectrum, and this has a sinx/x impulse response. These characteristics are known as a transform pair. In transform pairs, if one domain has one shape of the pair, the other domain will have the other shape. Thus a squarewave has a sinx/x spectrum and a sinx/s impulse has a square spectrum. FIG. 40 shows a number of transform pairs. Note the pulse pair. A time domain pulse of infinitely short duration has a flat spectrum. Thus a flat waveform, i.e.
DC, has only zero in its spectrum. Interestingly the transform of a Gaussian response in still Gaussian. The impulse response of the optics of a laser disk has a sin2 x/x2 function, and this is responsible for the triangular falling frequency response of the pickup.

FIG. 39 Fourier analysis of a squarewave into fundamental and harmonics.
A, amplitude; _, phase of fundamental wave in degrees; 1, first harmonic (fundamental);
2 odd harmonics 3-15; 3, sum of harmonics 1-15; 4, ideal squarewave.

FIG. 40 The concept of transform pairs illustrates the duality of the frequency
(including spatial frequency) and time domains.
The spectrum of a pseudo-random sequence is not flat because it has a finite sequence length. The rate at which the sequence repeats is visible in the spectrum. Where pseudo-random sequences are to be used in sample manipulation, i.e. where their effects can be audible, it is essential that the sequence length should be long enough to prevent the periodicity being audible.
FIG. 41 shows that the spectrum of a pseudo-random sequence has a sinx/x characteristic, with nulls at multiples of the clock frequency. A closer inspection of the spectrum shows that it is not continuous, but takes the form of a comb where the spacing is equal to the repetition rate of the sequence.
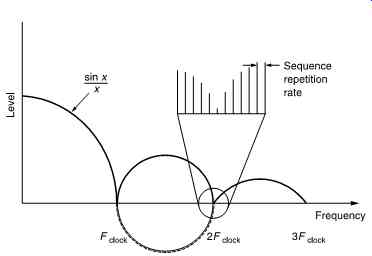
FIG. 41 The spectrum of a pseudo-random sequence has a sinx/x characteristic,
with nulls at multiples of the clock frequency. The spectrum is not continuous,
but resembles a comb where the spacing is equal to the repetition rate of the
sequence.
22. FIR and IIR Filters
Filters can be described in two main classes, as shown in FIG. 42, according to the nature of the impulse response. Finite-impulse response (FIR) filters are always stable and, as their name suggests, respond to an impulse once, as they have only a forward path. In the temporal domain, the time for which the filter responds to an input is finite, fixed and readily established. The same is therefore true about the distance over which a FIR filter responds in the spatial domain. FIR filters can be made perfectly phase linear if required. Most filters used for sampling rate conversion and oversampling fall into this category.

FIG. 42 An FIR filter (a) responds only to an input, whereas the output of
an IIR filter (b) continues indefinitely rather like a decaying echo.
Infinite-impulse response (IIR) filters respond to an impulse indefinitely and are not necessarily stable, as they have a return path from the output to the input. For this reason they are also called recursive filters.
As the impulse response in not symmetrical, IIR filters are not phase linear. In this respect they are similar to analog tone controls.

FIG. 43 (a) The impulse response of an LPF is a sinx/x curve which stretches
from - _ to + _ in time. The ends of the response must be neglected, and a
delay introduced to make the filter causal.

FIG. 43 (b) The structure of an FIR LPF. Input samples shift across the register
and at each point are multiplied by different coefficients.

FIG. 43 (c) When a single unit sample shifts across the circuit of FIG. 43(b),
the impulse response is created at the output as the impulse is multiplied
by each coefficient in turn.
23. FIR filters
A FIR filter works by graphically constructing the impulse response for every input sample. It is first necessary to establish the correct impulse response. FIG. 43(a) shows an example of a low-pass filter which cuts off at 1/4 of the sampling rate. The impulse response of a perfect low pass filter is a sinx/x curve, where the time between the two central zero crossings is the reciprocal of the cut-off frequency. According to the mathematics, the waveform has always existed, and carries on for ever.
The peak value of the output coincides with the input impulse. This means that the filter is not causal, because the output has changed before the input is known. Thus in all practical applications it is necessary to truncate the extreme ends of the impulse response, which causes an aperture effect, and to introduce a time delay in the filter equal to half the duration of the truncated impulse in order to make the filter causal.
As an input impulse is shifted through the series of registers in FIG. 43(b), the impulse response is created, because at each point it is multiplied by a coefficient as in (c). These coefficients are simply the result of sampling and quantizing the desired impulse response. Clearly the sampling rate used to sample the impulse must be the same as the sampling rate for which the filter is being designed. In practice the coefficients are calculated, rather than attempting to sample an actual impulse response. The coefficient wordlength will be a compromise between cost and performance. Because the input sample shifts across the system registers to create the shape of the impulse response, the configuration is also known as a transversal filter. In operation with real sample streams, there will be several consecutive sample values in the filter registers at any time in order to convolve the input with the impulse response.
Simply truncating the impulse response causes an abrupt transition from input samples which matter and those which do not. Truncating the filter superimposes a rectangular shape on the time domain impulse response. In the frequency domain the rectangular shape transforms to a sinx/x characteristic which is superimposed on the desired frequency response as a ripple. One consequence of this is known as Gibb's phenomenon; a tendency for the response to peak just before the cut-off frequency.

FIG. 44 The truncation of the impulse in an FIR filter caused by the use
of a finite number of points (N) results in ripple in the response. Shown here
are three different numbers of points for the same impulse response. The filter
is an LPF which rolls off at 0.4 of the fundamental interval. (Courtesy Philips
Technical Review)

FIG. 45 The effect of window functions. At top, various window functions
are shown in continuous form. Once the number of samples in the window is established,
the continuous functions shown here are sampled at the appropriate spacing
to obtain window coefficients. These are multiplied by the truncated impulse
response coefficients to obtain the actual coefficients used by the filter.
The amplitude responses I-V correspond to the window functions illustrated.
(Responses courtesy Philips Technical Review)

FIG. 46 The Dolph window shape is shown at (a). The frequency response is
at (b).
Note the constant height of the response ripples.
As a result, the length of the impulse which must be considered will depend not only on the frequency response but also on the amount of ripple which can be tolerated. If the relevant period of the impulse is measured in sample periods, the result will be the number of points or multiplications needed in the filter. FIG. 44 compares the performance of filters with different numbers of points. A high-quality digital audio FIR filter may need in excess of 100 points.
Rather than simply truncate the impulse response in time, it is better to make a smooth transition from samples which do not count to those that do. This can be done by multiplying the coefficients in the filter by a window function which peaks in the centre of the impulse. FIG. 45 shows some different window functions and their responses. The rectangular window is the case of truncation, and the response is shown at I. A linear reduction in weight from the centre of the window to the edges characterizes the Bartlett window II, which trades ripple for an increase in transition-region width. At III is shown the Hanning window, which is essentially a raised cosine shape. Not shown is the similar Hamming window, which offers a slightly different trade-off between ripple and the width of the main lobe. The Blackman window introduces an extra cosine term into the Hamming window at half the period of the main cosine period, reducing Gibb's phenomenon and ripple level, but increasing the width of the transition region. The Kaiser window is a family of windows based on the Bessel function, allowing various tradeoffs between ripple ratio and main lobe width. Two of these are shown in IV and V.
The Dolph window shown in FIG. 46 results in an equiripple filter which has the advantage that the attenuation in the stopband never falls below a certain level.

FIG. 47 A downsampling filter using the Hamming window.
Filter coefficients can be optimized by computer simulation. One of the best-known techniques used is the Remez exchange algorithm, which converges on the optimum coefficients after a number of iterations.
In the example of FIG. 47, a low-pass FIR filter is shown which is intended to allow downsampling by a factor of two. The key feature is that the stopband must have begun before one half of the output sampling rate. This is most readily achieved using a Hamming window because it was designed empirically to have a flat stopband so that good aliasing attenuation is possible. The width of the transition band determines the number of significant sample periods embraced by the impulse. The Hamming window doubles the width of the transition band. This determines in turn both the number of points in the filter and the filter delay. For the purposes of illustration, the number of points is much smaller than would normally be the case in an audio application.
As the impulse is symmetrical, the delay will be half the impulse period. The impulse response is a sinx/x function, and this has been calculated in the figure. The equation for the Hamming window function is shown with the window values which result. The sinx/x response is next multiplied by the Hamming window function to give the windowed impulse response shown.
If the coefficients are not quantized finely enough, it will be as if they had been calculated inaccurately, and the performance of the filter will be less than expected. FIG. 48 shows an example of quantizing coefficients. Conversely, raising the wordlength of the coefficients increases cost.

FIG. 48 Frequency response of a 49-point transversal filter with infinite
precision (solid line) shows ripple due to finite window size. Quantizing coefficients
to 12 bits reduces attenuation in the stopband. (Responses courtesy Philips
Technical Review)

FIG. 49 A seven-point folded filter for a symmetrical impulse response. In
this case K1 and K7 will be identical, and so the input sample can be multiplied
once, and the product fed into the output shift system in two different places.
The centre coefficient K4 appears once. In an even-numbered filter the centre
coefficient would also be used twice.
The FIR structure is inherently phase linear because it is easy to make the impulse response absolutely symmetrical. The individual samples in a digital system do not know in isolation what frequency they represent, and they can only pass through the filter at a rate determined by the clock. Because of this inherent phase-linearity, a FIR filter can be designed for a specific impulse response, and the frequency response will follow.
The frequency response of the filter can be changed at will by changing the coefficients. A programmable filter only requires a series of PROMs to supply the coefficients; the address supplied to the PROMs will select the response. The frequency response of a digital filter will also change if the clock rate is changed, so it is often less ambiguous to specify a frequency of interest in a digital filter in terms of a fraction of the fundamental interval rather than in absolute terms. The configuration shown in FIG. 43 serves to illustrate the principle. The units used on the diagrams are sample periods and the response is proportional to these periods or spacings, and so it is not necessary to use actual figures.
Where the impulse response is symmetrical, it is often possible to reduce the number of multiplications, because the same product can be used twice, at equal distances before and after the centre of the window. This is known as folding the filter. A folded filter is shown in FIG. 49.
24. Sampling-rate conversion
The topic of sampling-rate conversion will become increasingly important as digital audio equipment becomes more common and attempts are made to create large interconnected systems. Many of the circumstances in which a change of sampling rate is necessary are set out here:
1. To realize the advantages of oversampling converters, an increase in sampling rate is necessary prior to DACs and a reduction in sampling rate is necessary following ADCs. In oversampling the factors by which the rates are changed are very much higher than in other applications.
2. When a digital recording is played back at other than the correct speed to achieve some effect or to correct pitch, the sampling rate of the reproduced signal changes in proportion. If the playback samples are to be fed to a digital mixing console which works at some standard frequency, rate conversion will be necessary.
3. In the past, many different sampling rates were used on recorders which are now becoming obsolete. With sampling-rate conversion, recordings made on such machines can be played back and transferred to more modern formats at standard sampling rates.
4. Different sampling rates exist today for different purposes. Rate conversion allows material to be exchanged freely between rates. For example, master tapes made at 48 kHz on multitrack recorders may be digitally mixed down to two tracks at that frequency, and then converted to 44.1 kHz for Compact Disc or DCC mastering, or to 32 kHz for broadcast use.
5. When digital audio is used in conjunction with film or video, difficulties arise because it is not always possible to synchronize the sampling rate with the frame rate. An example of this is where the digital audio recorder uses its internally generated sampling rate, but also records studio timecode. On playback, the timecode can be made the same as on other units, or the sampling rate can be locked, but not both. Sampling-rate conversion allows a recorder to play back an asynchronous recording locked to timecode.
6. When programs are interchanged over long distances, there is no guarantee that source and destination are using the same timing reference. In this case the sampling rates at both ends of a link will be nominally identical, but drift in reference oscillators will cause the relative sample phase to be arbitrary.
In items 5 and 6 above, the difference of rate between input and output is small, and the process is then referred to as synchronization.
This can be simpler than rate conversion, and will be treated in section 8.

FIG. 50 Categories of rate conversion. (a) Integer-ratio conversion, where
the lower-rate samples are always coincident with those of the higher rate.
There are a small number of phases needed. (b) Fractional-ratio conversion,
where sample coincidence is periodic. A larger number of phases are required.
Example here is conversion from 50.4 kHz to 44.1 kHz (8/7). (c) Variable-ratio
conversion, where there is no fixed relationship, and a large number of phases
are required.
Sampling-rate conversion can be effected by returning to the analog domain. A DAC is connected to an ADC. In order to satisfy the requirements of sampling theory, there must be a low-pass filter between the two having a frequency response restricted to one-half of the lower sampling rate. In reality this is seldom done, because all practical machines have anti-aliasing filters at their analog inputs and anti-image filters at their analog outputs. Connecting one machine to another via the analog domain therefore includes one unnecessary filter in the chain.
Since analog filters are seldom optimal, degradation may be caused by rate-converting in this way, particularly in the area of phase response, although the introduction of oversampling convertors has lessened the problem.
Analog filters usually have a fixed response, and this is not necessarily the correct one if both input and output rates are to be varied significantly. The increase in noise due to an additional quantizing stage and additional double exposure to clock jitter is not beneficial. Methods of sampling-rate conversion in the digital domain are preferable and will be described here.
There are three basic but related categories of rate conversion, as shown in FIG. 50. The most straightforward (a) changes the rate by an integer ratio, up or down. The timing of the system is thus simplified because all samples (input and output) are present on edges of the higher-rate sampling clock. Such a system is generally adopted for oversampling convertors; the exact sampling rate immediately adjacent to the analog domain is not critical, and will be chosen to make the filters easier to implement.
Next in order of difficulty is the category shown at (b) where the rate is changed by the ratio of two small integers. Samples in the input periodically time-align with the output. Many of the early proposals for professional sampling rates were based on simple fractional relationships to 44.1 kHz such as 7. so that this technique could be used. This technique is not suitable for variable-speed replay or for asynchronous operation.
The most complex rate-conversion category is where there is no simple relationship between input and output sampling rates, and indeed they are allowed to vary. This situation, shown at (c), is known as variable-ratio conversion. The time relationship of input and output samples is arbitrary, and independent clocks are necessary. Once it was established that variable-ratio conversion was feasible, the choice of a professional sampling rate became very much easier, because the simple fractional relationships could be abandoned. The conversion fraction between 48 kHz and 44.1 kHz is 160:147, which is indeed not simple.
As the technique of integer-ratio conversion is used almost exclusively for oversampling in digital audio it will be discussed in that context.
Sampling-rate reduction by an integer factor is dealt with first.
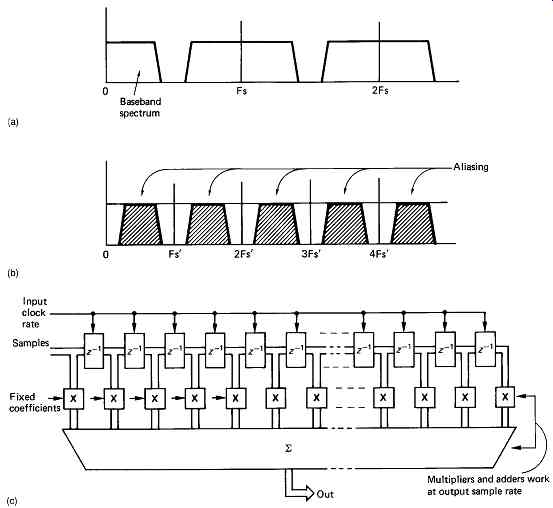
FIG. 51(a) shows the spectrum of a typical sampled system where the sampling
rate is a little more than twice the analog bandwidth.
Attempts to reduce the sampling rate by simply omitting samples, a process known as decimation, will result in aliasing, as shown in (b).
Intuitively it is obvious that omitting samples is the same as if the original sampling rate was lower. In order to prevent aliasing, it is necessary to incorporate low-pass filtering into the system where the cut-off frequency reflects the new, lower, sampling rate. An FIR type low-pass filter could be installed, as described earlier in this section, immediately prior to the stage where samples are omitted, but this would be wasteful, because for much of its time the FIR filter would be calculating sample values which are to be discarded.
A more effective method is to combine the low-pass filter with the decimator so that the filter only calculates values to be retained in the output sample stream. FIG. 51(c) shows how this is done. The filter makes one accumulation for every output sample, but that accumulation is the result of multiplying all relevant input samples in the filter window by an appropriate coefficient. The number of points in the filter is determined by the number of input samples in the period of the filter window, but the number of multiplications per second is obtained by multiplying that figure by the output rate. If the filter is not integrated with the decimator, the number of points has to be multiplied by the input rate. The larger the rate-reduction factor, the more advantageous the decimating filter ought to be, but this is not quite the case, as the greater the reduction in rate, the longer the filter window will need to be to accommodate the broader impulse response.
When the sampling rate is to be increased by an integer factor, additional samples must be created at even spacing between the existing ones. There is no need for the bandwidth of the input samples to be reduced since, if the original sampling rate was adequate, a higher one must also be adequate.

FIG. 51 The spectrum of a typical digital audio sample stream in (a) will
be subject to aliasing as in (b) if the baseband width is not reduced by an
LPF. In (c) an FIR low-pass filter prevents aliasing. Samples are clocked transversely
across the filter at the input rate, but the filter only computes at the output
sample rate.
Clearly this will only work if the two rates are related by an integer factor.
FIG. 52 shows that the process of sampling-rate increase can be thought of in two stages. First the correct rate is achieved by inserting samples of zero value at the correct instant, and then the additional samples are given meaningful values by passing the sample stream through a low-pass filter which cuts off at the Nyquist frequency of the original sampling rate. This filter is known as an interpolator, and one of its tasks is to prevent images of the lower input-sampling spectrum from appearing in the extended baseband of the higher-rate output spectrum.
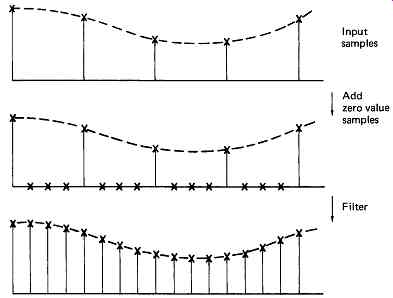
FIG. 52 In integer-ratio sampling, rate increase can be obtained in two stages.
Firstly, zero-value samples are inserted to increase the rate, and then filtering is used to give the extra samples real values. The filter necessary will be an LPF with a response which cuts off at the Nyquist frequency of the input samples.
How do interpolators work? It is important to appreciate that, according to sampling theory, all sampled systems have finite bandwidth.
An individual digital sample value is obtained by sampling the instantaneous voltage of the original analog waveform, and because it has zero duration, it must contain an infinite spectrum. However, such a sample can never be heard in that form because of the reconstruction process, which limits the spectrum of the impulse to the Nyquist limit.
After reconstruction, one infinitely short digital sample ideally represents a sinx/x pulse whose central peak width is determined by the response of the reconstruction filter, and whose amplitude is proportional to the sample value. This implies that, in reality, one sample value has meaning over a considerable timespan, rather than just at the sample instant. If this were not true, it would be impossible to build an interpolator.
As in rate reduction, performing the steps separately is inefficient. The bandwidth of the information is unchanged when the sampling rate is increased; therefore the original input samples will pass through the filter unchanged, and it is superfluous to compute them. The combination of the two processes into an interpolating filter minimizes the amount of computation.

FIG. 53 A single sample results in a sinx/x waveform after filtering in the
analog domain. At a new, higher, sampling rate, the same waveform after filtering
will be obtained if the numerous samples of differing size shown here are used.
It follows that the value of these new samples can be calculated from the input
samples in the digital domain in an FIR filter.
As the purpose of the system is purely to increase the sampling rate, the filter must be as transparent as possible, and this implies that a linear phase configuration is mandatory, suggesting the use of an FIR structure.
FIG. 53 shows that the theoretical impulse response of such a filter is a sinx/x curve which has zero value at the position of adjacent input samples. In practice this impulse cannot be implemented because it is infinite.
The impulse response used will be truncated and windowed as described earlier. To simplify this discussion, assume that a sinx/x impulse is to be used. The process of interpolation is the same in principle as the reconstruction filtering which takes place in DACs. It will be seen in section 4 that a continuous time analog signal is obtained by summing the analog impulses due to each sample. In a digital interpolating filter, this process is duplicated but in discrete time.

FIG. 54 A two times oversampling interpolator. To compute an intermediate
sample, the input samples are imagined to be sinx/x impulses, and the contributions
from each at the point of interest can be calculated. In practice, rather more
samples on either side need to be taken into account.

FIG. 55 In 4x oversampling, for each set of input samples, four phases of
coefficients are necessary, each of which produces one of the oversampled values.
If the sampling rate is to be doubled, new samples must be interpolated exactly halfway between existing samples. The necessary impulse response is shown in FIG. 54; it can be sampled at the output sample period and quantized to form coefficients. If a single input sample is multiplied by each of these coefficients in turn, the impulse response of that sample at the new sampling rate will be obtained. Note that every other coefficient is zero, which confirms that no computation is necessary on the existing samples; they are just transferred to the output. The intermediate sample is computed by adding together the impulse responses of every input sample in the window. The figure shows how this mechanism operates. If the sampling rate is to be increased by a factor of four, three sample values must be interpolated between existing input samples. FIG. 55 shows that it is only necessary to sample the impulse response at one-quarter the period of input samples to obtain three sets of coefficients which will be used in turn. In hardware implemented filters, the input sample which is passed straight to the output is transferred by using a fourth filter phase where all coefficients are zero except the central one which is unity.
FIG. 50 showed that when the two sampling rates have a simple fractional relationship m/n, there is a periodicity in the relationship between samples in the two streams. It is possible to have a system clock running at the least-common multiple frequency which will divide by different integers to give each sampling rate.
FIG. 56 In (a), fractional-ratio conversion of 3/4 in this example is by
increasing to 4x input prior to reducing by 3x. The inefficiency due to discarding
previously computed values is clear. In (b), efficiency is raised since only
needed values will be computed. Note how the interpolation phase changes for
each output. Fixed coefficients can no longer be used.
The existence of a common clock frequency means that a fractional ratio convertor could be made by arranging two integer-ratio convertors in series. This configuration is shown in FIG. 56(a). The input-sampling rate is multiplied by m in an interpolator, and the result is divided by n in a decimator. Although this system would work, it would be grossly inefficient, because only one in n of the interpolator's outputs would be used. A decimator followed by an interpolator would also offer the correct sampling rate at the output, but the intermediate sampling rate would be so low that the system bandwidth would be quite unacceptable.
As has been seen, a more efficient structure results from combining the processes. The result is exactly the same structure as an integer-ratio interpolator, and requires an FIR filter. The impulse response of the filter is determined by the lower of the two sampling rates, and as before it prevents aliasing when the rate is being reduced, and prevents images when the rate is being increased. The interpolator has sufficient coefficient phases to interpolate m output samples for every input sample, but not all of these values are computed; only interpolations which coincide with an output sample are performed. It will be seen in FIG. 56(b) that input samples shift across the transversal filter at the input sampling rate, but interpolations are performed only at the output sample rate. This is possible because a different filter phase will be used at each interpolation.
In the previous examples, the sample rate of the filter output had a constant relationship to the input, which meant that the two rates had to be phase-locked. This is an undesirable constraint in some applications, including sampling rate convertors used for variable-speed replay. In a variable-ratio convertor, values will exist for the instants at which input samples were made, but it is necessary to compute what the sample values would have been at absolutely any time between available samples. The general concept of the interpolator is the same as for the fractional-ratio convertor, except that an infinite number of filter phases is necessary. Since a realizable filter will have a finite number of phases, it is necessary to study the degradation this causes.
The desired continuous time axis of the interpolator is quantized by the phase spacing, and a sample value needed at a particular time will be replaced by a value for the nearest available filter phase. The number of phases in the filter therefore determines the time accuracy of the interpolation. The effects of calculating a value for the wrong time are identical to sampling with jitter, in that an error occurs proportional to the slope of the signal. The result is program-modulated noise. The higher the noise specification, the greater the desired time accuracy and the larger the number of phases required. The number of phases is equal to the number of sets of coefficients available, and should not be confused with the number of points in the filter, which is equal to the number of coefficients in a set (and the number of multiplications needed to calculate one output value).
In section 4 it will be shown that the sampling jitter accuracy necessary for sixteen-bit working is a few hundred picoseconds. This implies that something like 215 filter phases will be required for adequate performance in a sixteen-bit sampling-rate convertor.
The direct provision of so many phases is difficult, since more than a million different coefficients must be stored; so alternative methods have been devised. When several interpolators are cascaded, the number of phases available is the product of the number of phases in each stage. For example, if a filter which could interpolate sample values halfway between existing samples were followed by a filter which could interpolate at one-quarter, one-half and three-quarters the input period, the overall number of phases available would be eight. This is illustrated in FIG. 57.
For a practical convertor, four filters in series might be needed. To increase the sampling rate, the first two filters interpolate at fixed points between samples input to them, effectively multiplying the input sampling rate by some large factor as well as removing images from the spectrum; the second two work with variable coefficients, like the fractional-ratio convertor described earlier, so that only samples coincident with the output clock are computed. To reduce the sampling rate, the positions of the two pairs of filters are reversed, so that the fixed-response filters perform the anti-aliasing function at the output sampling frequency.

FIG. 57 Cascading interpolators multiplies the factor of sampling-rate increase
of each stage.
As mentioned earlier, the response of a digital filter is always proportional to the sampling rate. When the sampling rate on input or output varies, the phase of the interpolators must change dynamically.
The necessary phase must be selected to the stated accuracy, and this implies that the position of the relevant clock edge must be measured in time to the same accuracy. This is not possible because, in real systems, the presence of noise on binary signals of finite-rise time shifts the time where the logical state is considered to have changed. The only way to measure the position of clocks in time without jitter is to filter the measurement digitally, and this can be done with a numerically locked loop. FIG. 58 shows the essential stages of a variable-ratio convertor of this kind.

FIG. 58 (a) In a variable-ratio convertor, the phase relationship of input
and output clock edges must be measured to determine the coefficients needed.
Jitter on clocks prevents their direct use, and phase-locked loops must be
used to average the jitter over many sample clocks.

FIG. 58 (b) The clock relationships in (a) determine the relative phases
of output and input samples, which in conjunction with the filter impulse response
determine the coefficients necessary.
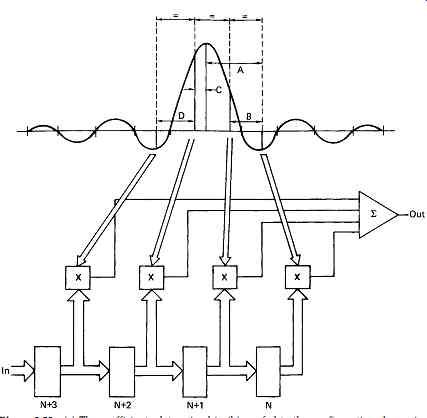
FIG. 58 (c) The coefficients determined in (b) are fed to the configuration
shown (or the equivalent implemented in software) to compute the output sample
at the correct interpolated position. Note that actual filter will have many
more points than this simple example shows.
When suitable processing speed is available, a digital computer can act as a filter, since each multiplication can be executed serially, and the results accumulated to produce an output sample. For simple filters, the coefficients would be stored in memory, but the number of coefficients needed for rate conversion precludes this. However, it is possible to compute what a set of coefficients should be algorithmically, and this approach permits single-stage conversion.
The two sampling clocks are compared as before, to produce an accurate relative-phase parameter. The lower sampling rate is measured to determine what the impulse response of the filter should be to prevent aliasing or images, and this is fed, along with the phase parameter, to a processor which computes a set of coefficients and multiplies them by a window function. These coefficients are then used by the single-filter stage to compute one output sample. The process then repeats for the next output sample.
25. IIR filters
FIG. 59 is a FIR filter which has been adapted in an attempt to simulate an RC network. Because an RC network is causal, i.e. the output cannot appear before the input, the impulse response is asymmetrical, and represents an exponential decay, as shown in FIG. 59(a). The asymmetry of the impulse response confirms the expected result that this filter will not be phase-linear. The structure of the filter is exactly the same as the earlier examples given in this section; only the coefficients have been changed. The simulation of RC networks is common in digital audio for the purposes of equalization or provision of tone controls. A large number of points are required in an FIR filter to create the long exponential decays necessary, and the FIR filter is at a disadvantage here because an exponential decay can be computed as every output sample is a fixed proportion of the previous one.

FIG. 59 In (a) an FIR filter is supplied with exponentially decaying coefficient
to simulate an RC response. In (b) the configuration of an IIR or recursive
filter uses much less hardware (or computation) to give the same response,
shown in (c).
FIG. 59(b) shows a much simpler hardware configuration, where the output is returned in attenuated form to the input. The response of this circuit to a single sample is a decaying series of samples, in which the rate of decay is controlled by the gain of the multiplier. If the gain is one, the output can carry on indefinitely. For this reason, the configuration is known as an infinite impulse response (IIR) filter. If the gain of the multiplier is slightly more than one, the output will increase exponentially after a single non-zero input until the end of the number range is reached. Unlike FIR filters, IIR filters are not necessarily stable. FIR filters are easy to understand, but difficult to make in audio applications; IIR filters are easier to make, because less hardware is needed, but they are harder to understand.
One major consideration when recursive techniques are to be used is that the accuracy of the coefficients must be much higher. This is because an impulse response is created by making each output some fraction of the previous one, and a small error in the coefficient becomes a large error after several recursions. This error between what is wanted and what results from using truncated coefficients can often be enough to make the actual filter unstable whereas the theoretical model is not.
By way of introduction to this class of filters, the characteristics of some useful configurations will be discussed. It will be seen that parallels can be drawn with some classical analog circuits.

FIG. 60 (a) First-order lag network IIR filter. Note recursive path through single
sample delay latch. (b) The arrangement of (a) becomes an integrator if K2
= 1, since the output is always added to the next sample. (c) When the time
coefficients sum to unity, the system behaves as an RC lag network. (d) The
same performance as in (c) can be realized with only one multiplier by reconfiguring
as shown here.

FIG. 61 The response of the configuration of FIG. 60 to a unit step. With
K2 = 1, the system is an integrator, and the straight line shows the output
with K1 = 0.1. With K1 = 0.1 and K2 = 0.9, K1 + K2 = 1 and the exponential
response of an RC network is simulated.
The terms phase lag and phase lead are used to describe analog circuit characteristics, and they are also applicable to digital circuits. FIG. 60(a) shows a first-order lag network containing two multipliers, a register to provide one sample period of delay, and an adder. As might be expected, the characteristics of the circuit can be transformed by changing the coefficients. If K2 is greater than unity, the circuit is unstable, as any non-zero input causes the output to increase exponentially. Making K2 equal to unity ( FIG. 60(b)) produces a digital integrator, because the current value in the latch is added to the input to form the next value in the latch. The coefficient K1 determines the time constant in the same way that the RC network does for the analog circuit.
FIG. 60(c) shows the case where K1 + K2 = 1; the response will be the same as an RC lag network. In this case it will be more economical to construct a different configuration shown in (d) having the same characteristics but eliminating one stage of multiplication. The operation of these configurations can be verified by computing their responses to an input step. This is simply done by applying some constant input value, and deducing how the output changes for each applied clock pulse to the register. This has been done for two cases in FIG. 61 where the linear integrator response and the exponential responses can be seen. It is interesting to experiment with different coefficients to see how the results change.

FIG. 62 (a) First-order lead configuration. Unlike the lag filter this arrangement
is always stable, but as before the effect of changing the coefficients is
dramatic. (b) When K2 of (a) is made zero, the configuration subtracts successive
samples, and thus acts as a differentiator. (c) Setting K2 of (a) to unity
gives the high-pass filter response shown here.
FIG. 62(a) shows a first-order lead network using the same basic building blocks. Again, the coefficient values have dramatic power. If K2 is made zero, the circuit simply subtracts the previous sample value from the current one, and so becomes a true differentiator as in (b). K1 determines the time constant. If K2 is made unity, the configuration acts as a high-pass filter as in (c).