By Michael W. King
ONE OF THE PROBLEMS in hi-fidelity system design is that of a crossover network to divide the output spectrum into portions suitable for high and low frequency loudspeaker drivers. In the past, this has been achieved with the use of passive filters, as shown in Figure 1A. The disadvantage of this system is the non-constant input impedance of a direct-radiator loudspeaker. A solution to this problem has been proposed by Ashley and Kaminsky, employing a system like that shown in Figure 1B. In this system filtering is accomplished at low levels and the speakers are driven by low output impedance buffer amplifiers. Clearly, this isolates the driving point impedance of the loudspeakers from the output of the filter; and, in addition, the input impedance of the buffer amplifier can be made virtually any value of pure and constant resistance making this system also suitable for use with passive filters. In addition, it should also be noted that the typical passive network of Figure 1A requires capacitances on the order of tens of microfarads, which are expensive and difficult to obtain, while the active network of Figure 1B requires capacitors on the order of nanofarads, reducing the cost differential between the two systems.
Following Ashley and Kaminsky, a filter as shown in Figure 2 was constructed. This is an asymmetrical third-order network where the high-pass has a third-order Butterworth characteristic. Here the high-pass is achieved by an active filter and the low-pass portion is derived by subtraction of the high-pass signal from the total input signal. This design is of the constant voltage type described by Ashley and Small, meaning that the phasor sum of the outputs of the filter is equal to some constant in the frequency domain. Because of this, given perfect drivers and amplifiers, the total acoustic output signal will be a perfect reproduction of the source material. This can be demonstrated, as shown below by adding the transfer functions of the high and low pass filters to give the transfer function for the sum of the outputs.
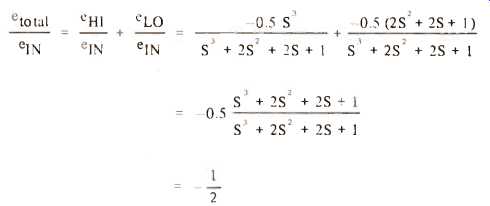
Thus, this network has a gain of one-half which is constant with respect to frequency. The filter was designed for a gain of one-half in order to simplify component values and to avoid problems caused by excessive levels.
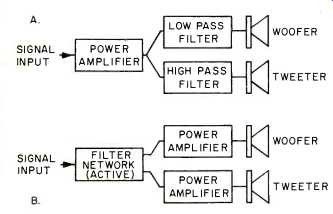
Fig. 1-Possible crossover-amplifier arrangements.
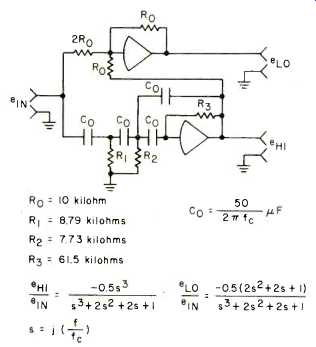
Fig. 2-Active filter network.

Fig. 3--Measured response of I.C. filter network.
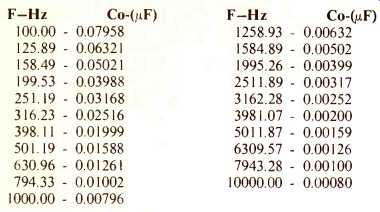
Table 1--Capacitor values for active filter network.
A µA741 operational amplifier was chosen because of its high gain and wide range of operating voltages. This was chosen over the popular µA709 operational amplifier because the 741 requires no external frequency compensation. Supply voltage of ± 15v was chosen because this was most compatible with the commercially available integrated-circuit power amplifiers and it was intended that both filter and buffer amplifiers could be powered from a common supply.
For this network, the slope of the high-pass characteristic in the stop-band is 18 dB per octave and the phase goes from-180 degrees in the passband to 90 degrees in the stop-band, with -45 degrees at the crossover frequency. For the low pass, the stop-band slope is 6 dB per octave and the phase response goes from-180 degrees in the pass-band to -270 degrees in the stop-band with approximately-180 degrees of phase shift at the crossover frequency. Ideally, perhaps, the phase shift in the pass-bands would be zero degrees; however, the operational amplifiers require an additional -180 degrees for stability because of the feedback employed. Note also that a filter could have been synthesized by deriving the low-pass and subtracting to obtain the high-pass. This would also be a constant voltage network and for a third-order low-pass would have an 18 dB per octave slope for the high-pass. The disadvantage to this arrangement is that, because of the greater energy in the low-frequency portion of the spectrum, the tweeter would be forced to handle considerably more power because of the lesser stop-band slope, and this might adversely affect reliability. Furthermore, because of their built-in inductance and reasonably civil behavior above the usual cutoff frequencies, today's low-frequency drivers are more suitable for use with a 6 dB per octave stop-band slope.
Component values were selected from Table IV of Ashley and Kaminsky's paper,' which is reproduced here as Table 1, for a crossover frequency of 1584.89, which is suitable for an 8-in. woofer. The values specified by Ashley and Kaminsky are: R0 = 10 Kilohm, R1 = 8.79 Kilohm, R2 = 7.73 Kilohm, R3 = 61.5 Kilohm, C0 = 5.02 Nanofarad
Since these values are not readily available, some change was, necessary as shown below.
R0 = 10 Kilohm, R1 = 8.79 Kilohm, R2 = 7.8 Kilohm, R3 = 60.7 Kilohm, C0 = 5.0 Nanofarad
This was found to have a negligible effect on the actual response, as demonstrated by the fact that the measured -3 dB point of the high-pass signal (crossover frequency) was 1.55 kHz which is in error by less than 5 percent.
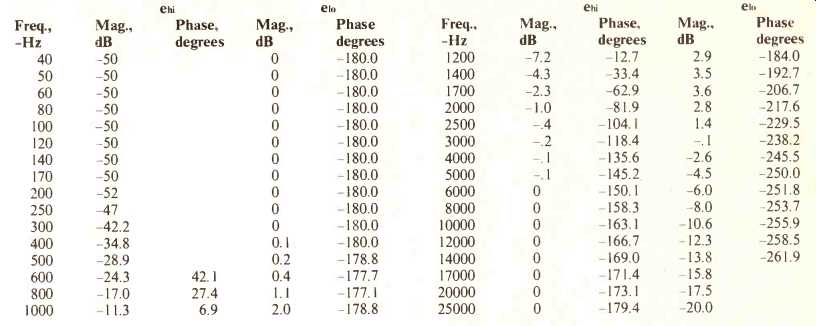
Table 2--Measured response of I.C. active filter.
The measured frequency response is as shown in Table 2 and Fig. 3. We note that this is a very flat curve without unexplained bumps and glitches that sometimes plague passive networks of this kind. Also note that the stop-band slopes and phase response are as predicted by myself, and Ashley and Kaminsky. In short, it is felt that the active filter network is. a good performing, easy to realize alternative to the passive networks used in the past. In addition, given the relatively more common component values used as compared with a passive network for a similar function and the low cost of integrated-circuit operational amplifiers (the µA741 is available for less than $1.00), the cost differential should not be excessive.
References
1. L. L. Beranek, Acoustics, (McGraw-Hill, New York, 1954).
2. J. R. Ashley and A. L. Kaminsky, "Active and Passive Filters as Loudspeaker Crossover Networks," J. Audio Eng. Soc., 19, 494 (1971).
3. J. R. Ashley, "On the Transient Response of Ideal Crossover Networks," J. Audio Eng. Soc., Vol. 10, No. 3, 241.
4. R. H. Small, "Constant-Voltage Crossover Network Design," Proc. I.R. E.E. Australia, 31, 66 (1970).
5. J. R. Ashley and L. M. Henne, "Operational Amplifier Implementation of Ideal Electronic Crossover Networks," J. Audio Eng. Soc., 19, 7 (1971).
(Audio magazine, Apr. 1972)
Also see:
Crossover Network Design (Mar. 1972)
What Price Loudspeaker Response Curves (Mar. 1972)
The Acoustic Feedback Loudspeaker System (Jan. 1972)
Speaker Tests: Room Test by Richard C. Heyser (Jan. 1975)
Speaker Q's and A's Mainly for Beginners (Mar. 1972)
Speaker Tests--Phase Response (by Richard C. Heyser) (Dec. 1974)
= = = =