by KEN POHLMANN

CHOMPING UP THE BITS

Now that we've had conflicts in the Persian Gulf, Afghanistan, the West Bank, and the pool area of my condominium, it looks like the next trouble spot will be in CD player design. Specifically, the configuration controversy surrounding the digital-to-analog converter (D/A) is heating up fast.

However you configure them, D/As represent a weak link in the signal chain; they are not always good at generating the analog voltages which represent the digital words read from the disc. In particular, low-amplitude distortion is sometimes introduced be cause, simply, 16-bit converters are not ideal for reliably converting 16-bit data.

The problem is understandable. A 16-bit D/A must determine which of its 65,536 output analog voltages corresponds to the input digital word, and it has perhaps 20 uS to make up its mind. (This could make for a very challenging game show.) Several problems can interfere with that decision.

For example, the distance between steps may not be exactly equidistant; that would lead to nonlinearity in the conversion. One solution is to use a D/A converter that can handle more than 16 bits. An 18-bit D/A, for example, would have 262,144 output levels, exactly four times as many as a 16-bit converter. Any nonlinearities from an 18-bit converter would therefore be correspondingly smaller, and the sound from a CD player using it would be theoretically better. In other words, an 18-bit converter would give a better 16-bit conversion. Out of this reasoning, the quest for more bits' worth of conversion was born.

Yamaha was the first to rock the boat, with a "Hi-Bit" system that offers 18-bit resolution using 16-bit D/As. The system, sometimes called quasi-18-bit, works something like this: Thanks to the multiplication going on inside a digital oversampling filter (which pre cedes the D/A), words longer than 16 bits are output at an oversampled rate.

In the Hi-Bit system, 18 bits from the filter are wired through switches to two 16-bit D/A converters (one for each channel). When all 16 bits are being used to convey a signal (as is the case when signal amplitude is high), the up per 16 bits are applied to the 16-bit converters, as usual. When signal amplitude is low, the two upper bits from the oversampling filter are not being used to convey information; hence, the 18 bits are shifted upward so that the unused bits are ignored, and the 16 lower bits are decoded instead. Through bit-shifting, a 16-bit converter may thus handle an 18-bit input. When the lower bits are shifted up, the output amplitude increases. To compensate for the shift in amplitude caused by shifting bits, the gain of the signal is reduced whenever the lower bits are shifted in. An attenuator downstream of the D/A handles this chore. The result of all this: An increased S/N ratio.

Of course, Yamaha's competition wasn't far behind. Technics has stepped in with a CD player conversion system employing no fewer than four digital-to-analog converters. They call it their "4-DAC 18-Bit High Resolution System." It too is intended to pro vide a cleaner conversion of a CD's 16-bit output than any single 16-bit converter alone could provide.

As with the Yamaha system, digital oversampling filtering and 16-bit D/A are employed, as well as bit-shifting However, in this design two D/As are used per channel, one for the positive half of the bipolar analog output wave form and one for the negative half. The reason for this (and the reason under lying any move toward more converters or more bits) is the desire to improve low-amplitude resolution. In this case, the design specifically addresses a problem known as crossover distortion.

This has always been an obstacle in reproducing low-level signals. Cross over distortion occurs at the zero crossing point between the positive and negative halves of the waveform; as polarity changes, the converter must switch all of its digits instantaneously (from 0111111111111111 to 1000000000000000). To accomplish this, an internal network of laser trimmed resistors must be switched, often with a slight crossover glitch.

That glitch is particularly troublesome when the player is reproducing low level signals because it's of fixed amplitude and is thus proportionally larger with respect to such signals. To remove the glitch, some manufacturers go to extreme lengths, such as the hand-tweaking of each D/A converter.

Crossover distortion can also be alleviated by providing a D/A for each waveform polarity; in that way, the dreaded total switching of digits never occurs within a single D/A converter. Of course, this does mean that the digital signal must be split between the two D/As, but an upstream processor chip can handle the switching digitally, in glitch-free fashion.

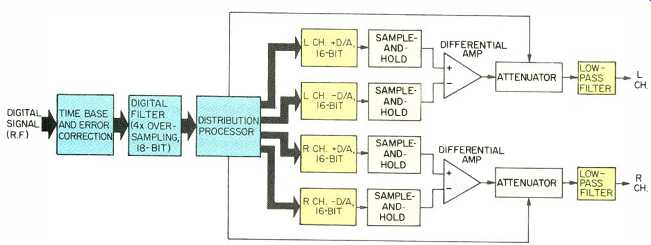
Fig. 1--Block diagram, Technics 4-DAC CD player. Note the use of separate D/A converters for each half of the signal waveform and bit-shifting (with subsequent attenuation) to get 18-bit resolution from 16-bit D/A chips.

Let's consider the circuit's signal flow, as shown in the block diagram of Fig. 1. A four-times oversampling filter outputs 18-bit words to the distribution processor, which directs the appropriate portion of the waveform to the correct D/A. A sample-and-hold circuit compensates for aperture error (a slight high-frequency roll-off) in the analog output. The two waveform halves are joined at the output by a differential amplifier. An attenuator compensates for the gain change caused by shifting, and a low-pass filter provides final attenuation of supersonic components.

The circuit operates similarly to Yamaha's bit-switching design. When the signal is of high amplitude, there is little motive to jump through hoops for greater low-amplitude resolution, so there is no bit shifting, and straight 16 bit conversion takes place. Both the positive-half and negative-half D/A converters in each channel reproduce the entire waveform, and their outputs are combined in a differential push-pull mode.

When the signal drops below -12 dB, the 4-DAC circuit gets serious.

First, it reads the most significant bit (MSB). If the value of the bit is high, the word has positive polarity, and thus it is directed to the positive-polarity D/A converter. Likewise, if the MSB is low, the negative-half D/A gets the word.

Also, when the signal is below -12 dB, the second most significant bit ceases to change; it will then always be low when the MSB is high, and high when the MSB is low. Because these two bits are spoken for, the word sent to the 16-bit D/As may be shifted down two bits. The D/As thus receive bits 3 through 18. Since the gain of the signal increases when bits are shifted, the attenuators are switched in to proportionally reduce gain.

Significantly, in this system the 17th and 18th bits from the oversampling filter have been utilized in reproducing the waveform, instead of being truncated and thrown away. Moreover, be cause dual D/As are used to convert the bipolar waveform, crossover distortion has been avoided. Together, these benefits pay dividends when reproducing low-level audio signals.

In fact, next time you listen to music, take a look at a VU meter. You'll ob serve that most music spends the greater part of its time below -12 dB.

In other words, the benefits of the 4 DAC system are usually present.

Straight 16-bit operation occurs only at high levels, usually of brief duration, when the amplitude of the waveform largely masks converter nonlinearities anyway.

In all, the 4-DAC design, used in tandem with quasi-18-bit technology, is a good approach to resolving the problem of nonlinearities in CD players' 16-bit converters. Of course, with recent advances in chip technology, true 18-bit D/A converters are now being produced and are appearing on the market in a growing number of CD players. All this activity is evidence of greater concern about this hitherto-overlooked weak link in the design of CD players.

So, how do CD players equipped with the 4-DAC system perform? Does this attention to two extra bits make any difference sonically? I'll leave the answers to those questions up to Len Feldman, Audio's resident evaluator of CD players. I love it when he gets me off the hook.

(adapted from Audio magazine, Jun. 1988)

= = = =