FOLD OVER BEETHOVEN

In the history of audio, I doubt whether any topic has provoked as much controversy, enthusiasm, and condemnation as has digital audio. I think that is to be expected; no other technological breakthrough has so thoroughly shaken things up. A lot of analog investment and expertise has been threatened and incredible opportunity has been created for newcomers. The idea of scrapping all present recording and reproduction equipment and relegating to antiquity all analog recordings, challenging all analog recording technique, and replacing all of that with new hardware, software, and method-yes, I think that might lead to a few discussions. Will digital audio prevail, or end up in the garage with your quadraphonic decoder? The answer is clear in my mind, but for those of you still wondering, keep reading and follow the evolution of the greatest coup in audio history.
Thus far we've covered some of the fundamentals of digital audio such as sampling and quantizing and held the presentation at a fairly general level.
Now I would like to delve a little deeper into some of the promises and pitfalls of digital audio. One particular challenge to the audio digitization system designer is that of aliasing, a kind of sampling confusion that can take place in the recording side of the chain. Just as a criminal can take two names, and thus confuse his identity, a sampled signal can be mistaken for another if aliasing is allowed to occur.
It is thus the designer's obligation to prevent aliasing from ever occurring; as we will see, an input low-pass filter will accomplish this, but only if its cutoff frequency is carefully chosen.
What is aliasing? It is a digital system's improper, but inevitable, response to an input signal whose frequency is out of bounds-that is, more than half the sampling frequency. Nyquist has shown that the highest signal frequency in a sampling system can be no more than half the sampling frequency. As the signal frequency becomes higher and higher, the number of sample points per cycle becomes fewer. When the signal frequency reaches half the sampling frequency, there are only two samples per cycle, which is the absolute minimum needed to record the bipolar nature of the waveform.
If we defiantly attempt to sample even higher frequencies, the sampler will continue to produce samples at its fixed rate, and these deviate audio frequencies are, indeed, recorded-but spurious new frequencies are "recorded" as well. As the deviate frequencies go higher and higher, new descending frequencies are created. Specifically, if S is the sampling rate and F is a frequency higher than half the sampling rate, then a new sampling frequency Ff is also created at Ff = S-F. For example, if S = 44 kHz, and we attempt to sample a 23-kHz signal, another sampled frequency appears at 21 kHz, if we attempt to sample a 24-kHz signal, 20 kHz appears. In other words, a new frequency appears back in the audio band, folded over from the sampling frequency. In fact, it is affectionately called foldover, or as the more literate types call it-aliasing.
To further elaborate upon this depressing scenario, in which a false frequency accompanies the actual frequency following the sampler, we must remember that a low-pass filter is used at the output of a digitization system to smooth the staircase function and thus recover the original signal. That output filter will be designed to cut at half the sampling frequency; thus our errant input frequencies which were above that value would be filtered out, and we would be left with only the aliased frequency running around our audio band. That isn't all-but before we consider further ramifications of this nasty business, let's take a look at an example.
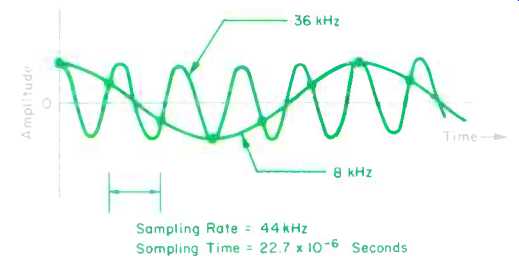
Fig. 1--Digital samples from a signal higher than half the sampling frequency
are identical to those from a signal of lower frequency. Here, a 36-kHz input
masquerades as an 8-kHz signal.
Suppose we have a digitization system sampling at 44 kHz. Further, suppose that a signal with a frequency of 36 kHz has somehow sneaked into our sampler. Our sampler would obediently produce the samples shown in Fig. 1, faithfully recording a series of amplitude values at sample times. Given those samples, could you decide which signal was the intended one--36 kHz, or 8 kHz? No-but don't feel bad, because no device, digital or otherwise, could distinguish either. After the output filter, the 36-kHz signal is gone, but the 8-kHz signal remains, containing samples as innocuous as any legitimate 8-kHz signal. What does that unwanted signal give to the fidelity of our audio system? Distortion.
Aliasing is about as bad as being trapped in a house of mirrors. If you were sampling at 44 kHz, an input frequency from 0 Hz to 22 kHz would sound fine, but as the frequency ranged from 22 to 44 kHz, we would hear it returning as a frequency descending from 22 kHz to 0 Hz. If we persevered, and raised the frequency from 44 to 66 kHz, it would appear again from 0 Hz to 22 kHz.
As if that weren't bad enough, we must complete our discussion with a look at the different manifestations of aliasing. First, aliasing occurs not only around the sampling frequency, but also from multiples of the frequency.
For example, all of these components would be produced in an aliasing scenario: S ± F, 2S ± F, 3S ± F, etc.
Thus in our example of a 44-kHz sampler and a 36-kHz input signal, some of the resulting frequencies would be: 8, 52, 80, 96, 124, 168 kHz, etc. That sure looks nasty, although only the S-F component will bother us directly as an interfering frequency.
Second, more complex tones exaggerate the problem. Our simple sine-tone examples have limited foldover to one and only one frequency. With more complex tones, aliasing frequencies could be generated separately for each harmonic.
For example, a tone of 5 kHz would normally have harmonics at 10, 15, 25 and 30 kHz. With digital sampling at 44 kHz, however, the 25-kHz fifth harmonic would fold over to 19 kHz, and the sixth harmonic (30 kHz) would pop in at 14 kHz, just shy of the 15-kHz third harmonic. A particularly loathsome kind of distortion, akin to intermodulation distortion, would result.
After this look at aliasing, you digital enthusiasts out there are perhaps ready to smash your CDs. But hold it! As bad as aliasing might be, in practice it isn't so bad. In fact, in a well-designed digital-recording system, it doesn't exist at all. The solution is simple. We merely bandlimit the input frequencies, with a sharp low-pass filter designed to provide a healthy attenuation of 60 dB or more at half the sampling rate, to make sure the throughput never exceeds half that frequency.
Neither disallowed fundamentals nor partials are allowed to enter the sampler, thus aliasing cannot occur. If those frequencies don't exist, neither will aliasing. No need to worry about something that isn't there.
But if the problem of aliasing upsets you, I'll be happy to take such CDs off your hands, especially Beethoven works. Just send them care of Audio.
(adapted from Audio magazine, Oct 1984; KEN POHLMANN )
= = = =