Advantages of FM. Although many improvements had been made in radio since the days of the first radio receiver, it was not until the advent of frequency modulation that noise interference was efficiently reduced in radio reception. Noise interference, for the most part, is due to sources, either man-made or natural, that are external to the receiver. Much of the worst interference comes from natural sources, generally beyond the power of man to control. AM receiver circuits and systems designed by engineers were of limited effectiveness in their suppression of interference. The best solution seemed to be the employment of brute-force method, using high powered radio signals to override the disturbing interference. In AM sets the signal-to-noise ratio had to be of the order of 100 to 1 or more to obscure the noise. With the use of frequency modulation, however, it became possible to reduce considerably the strength of the signal required to over ride the noise. Although the signal at the receiver input must still possess greater power than the undesired voltage, the signal-to-noise ratio in FM receivers need be only 2 to 1. [1]
[1. In a properly designed FM set it is possible for the signal-to-noise ratio to drop below 2 to 1 and still have the signal override any noise present. However, to be on the conservative side, the 2 to 1 ratio value will be retained.]
The ability of frequency modulation signals to override interference with low signal-to-noise ratios indirectly permits the use of many more stations within a given area than is possible with amplitude modulation. At the receiver, the desired signal must be only twice as strong as the undesired signal to hide the interference completely. Consider how much farther away an unwanted AM broadcasting station can be and still ruin reception: with AM a voltage only 1/100 as strong as the desired carrier will provide sufficient interference to be heard in the output of the receiver. Listen some night to an AM receiver, especially at the high frequency end of the band.
Signals, not only from nearby communities but from localities hundreds and thousands of miles distant, ride in to add their voice to a complete hodge-podge of whistles and signals, an intolerable situation for intelligible listening. Bring into play a 2 to 1 signal-to-noise ratio attainable with FM, and with one quick sweep 99 percent of the disturbance is eliminated. Now only signals from stations in the immediate vicinity are recognizable, and F.C.C. regulations do not permit simultaneous use of similar frequencies in the same service area.
It is quite popularly supposed that FM is capable of providing greater fidelity of reproduction than AM. This advantage is real, but it is an indirect benefit that results from FM's ability to eliminate more of the interference and thereby provide a signal at the receiver that adheres more closely to the original signal at the studio. But greater fidelity is not an intrinsic, direct characteristic of the process of frequency modulation itself. Fidelity is a result of the correct design of the various stages that form either system of transmission and, since the same basic components are present in each system, both have fundamentally the same potentiality of good fidelity.
Indirectly, we find other limitations, aside from the circuits themselves, that contribute to provide better fidelity with FM. For example, with AM only audio frequencies extending to 5000 cycles are transmitted, a limitation employed to prevent each station from occupying too great a frequency range within the limited AM broadcast band and to permit additional stations to operate. FM, arriving on the broadcast scene later, had the advantage of operating at the higher frequencies, where spectrum space is more plentiful.
Add to this the already noted intrinsic tendency of FM completely to over ride an interfering signal, and it is apparent why the misconception exists concerning fidelity. With the proper care in design, amplitude modulation can provide the listener with just as much fidelity as he obtains with FM. AM versus FM. In order to understand why FM proves so effective in reducing interference, we must first make a thorough investigation of the properties of a frequency-modulated wave. Perhaps the easiest way of be ginning is by a comparison of the effects on a carrier wave when it, is amplitude-modulated and when it is frequency-modulated.
When a continuous, radio-frequency carrier wave is amplitude-modulated, the amplitude is varied in a manner determined by the audio-modulating voltage. Refer to Fig. 1.1 in which the high-frequency carrier and the low-frequency modulating wave are shown separately. By applying the carrier to the grid of a tube, and then varying the tube's plate voltage in accordance with the modulating voltage, we obtain at the output the amplitude-modulated wave shown in Fig. 1.1C. The variations imposed onto the carrier contain the intelligence of the audio wave. Now the AM signal can be transmitted over the high-frequency circuits, through the air and to the receiver. At the receiver, the 2nd detector converts the amplitude variations to their original form, in which they become intelligible at the loudspeaker.
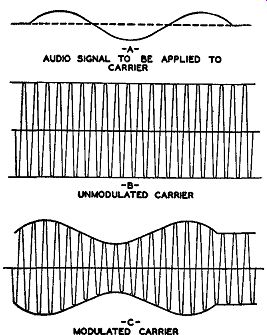
Fig. 1.1. The components of an amplitude-modulated wave.
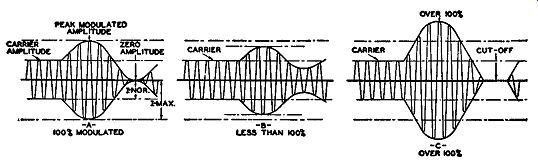
FIG. 1.2. Various degrees of amplitude modulation.
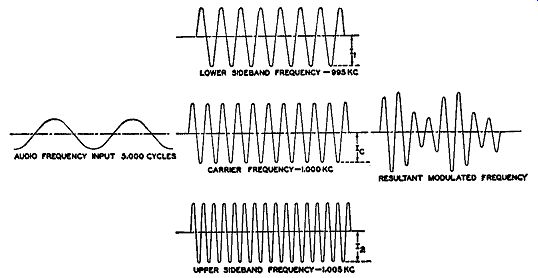
Fig. 1.3. The sidebands generated with amplitude modulation.
A closer inspection of the modulated wave, Fig. 1.1C, reveals that there are certain limitations to the strength of the audio-modulating voltage. For example, it must not be too large. A small modulating voltage will affect slightly the amplitude of the carrier, and the resultant variations will be identical with those of the modulating wave. This means that no distortion, or loss of fidelity, has occurred. Increasing the strength of the modulating voltage causes correspondingly greater rises and indentations in the final signal waveform, but the essential form of the audio voltage is still preserved. However, when the applied modulating voltage becomes too great, the carrier be comes highly distorted. An example is shown in Fig. 1.2C. For the maximum modulation with no distortion the modulating voltage can only decrease the amplitude of the carrier to zero, momentarily, or raise it to twice the normal value at the peaks. We have now what is commonly known as 100 percent modulation. Anything less is under-modulation; anything more is overmodulation. Of the two, under-modulation is to be preferred because, although it results in less power at the 2nd detector, it does not introduce any appreciable distortion. By distortion, we refer to the change in the shape of a wave from its original form.
The degree of modulation of a carrier wave is generally expressed as a percentage. It is the ratio of the peak amplitude of the modulating signal to the peak amplitude of the higher frequency carrier. The word "peak" is used because each of these waves are varying sinusoidally and one reference point is necessary. Mathematically, the ratio is expressed as
K=::!!!:.. 1m
Where … 1m = peak value of the modulating signal
1m = peak value of the carrier
When this ratio is equal to 1, we have 100 percent modulation wherein the amplitude of the modulated wave rises to twice the normal carrier value and decreases to zero when the two voltages act in opposition (see Fig. 1.2A). The process of varying the amplitude of a continuous carrier wave causes the appearance of frequencies in addition to that of the carrier. Where a single, audio sine wave is used as the modulating voltage, two additional frequencies are generated, each separated from the carrier frequency by an amount equal to the audio-modulating frequency. As an illustration, consider the case of a 1000- khz carrier modulated by a 5- khz audio note. If an analysis is made of the amplitude-modulated wave at the transmitter output, we will find that its components are the 1000- khz carrier, a frequency of 1005 khz, and one of 995 khz. Of the two additional frequencies produced, one is located above the carrier whereas the other is located the same frequency distance below the carrier. Together, these new frequencies are designated as sidebands. Graphically, they may be represented as shown in Fig. 1.3.
Now, obviously, the additional frequencies must in some way be related to the modulating voltage (which contains the desired intelligence), for with the removal of this voltage we find that the sidebands are no longer present. Without modulation only the carrier remains. The moment we speak into a microphone, however, a modulating voltage appears and, co incidentally, the sidebands. A mathematical and experimental analysis reveals that all of the extra power contained in the modulating signal goes directly into the sidebands. The carrier itself is left untouched. Thus, al though it may not be apparent from an inspection of Fig. 1.2, amplitude modulation gives rise to new frequencies, and these frequencies contain all the power and intelligence of the modulating voltage.
In all transmitting and receiving networks, provision must be made to include these sidebands. With a modulating frequency of 5000 cycles, or 5 khz, sidebands located ±5 khz from the carrier are formed, making it necessary to receive a bandwidth of 10 khz ( ±5 khz) wide. Anything less will partially or totally eliminate the sidebands, suppressing part or all of the intelligence. Although only one modulating frequency is mentioned, i.e., 5 khz, it is understood that any audio frequency may be used. Generally, the F.C.C. restricts the highest audio frequency to 5 khz, but this is only to limit the bandwidth of each station to 10 khz. Consequently, more stations per band are accommodated.
Frequency Modulation. In FM we maintain the amplitude constant and alter the carrier frequency. In this instance, both the amplitude and phase of the carrier are fixed, while the frequency shifts back and forth about one central position in accordance with an audio-modulating voltage.
This process is somewhat analogous to amplitude modulation, where the amplitude of the carrier is increased and decreased about the average, normal value.
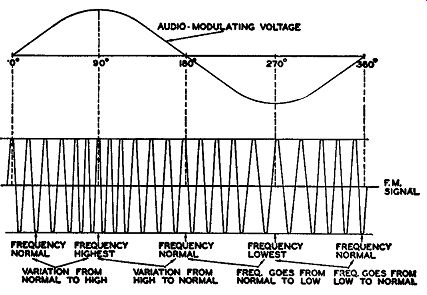
Fig. 1.4. Frequency variation in an FM signal.
The physical appearance of a wave that has been frequency-modulated by a sine wave is shown in Fig. 1.4. At each instant throughout the application of the modulating signal, the frequency of the carrier will depend directly upon the amplitude of the audio signal. At the start of the audio cycle, the frequency of the carrier is slightly affected because within this region the modulating voltage is small. As the audio cycle approaches its positive peak, at 90°, the frequency variation of the carrier from its mean or resting position also reaches a maximum. Between 90° and 180° of the audio cycle, the voltage is returning to zero and the modulated carrier is shifting back, in step, to its resting position. Continuing on to 270°, we see that the audio voltage is again rising, although this time in a negative direction. The carrier frequency is likewise going in a negative direction, as indicated by a lower frequency. At 270°, the carrier frequency is at its lowest point. From here it slowly follows the audio voltage back to normal. This occurs at 360°, after which a new cycle begins.
To summarize, we see that the frequency variations of the carrier are in step, at all times, with the amplitude variations of the applied modulating voltage. As the amplitude of this latter voltage rises, the frequency of the carrier likewise increases, 2 whereas, when the audio signal reverses and moves to the opposite polarity, the carrier frequency decreases correspondingly.
The variation in carrier frequency is wholly dependent upon the amplitude of the acting audio voltage and not at all on its frequency. This is similar to AM where the changes in carrier amplitude are influenced only by the amplitude of the audio signal. The frequency of the audio voltage, in both forms of modulation, determines the rapidity with which the amplitude or frequency changes take place but exerts no influence on the extent of these changes. A strong audio signal, at any frequency, will cause a wide frequency deviation from the center or resting frequency; a low or weak audio signal will cause less frequency variation. The frequency of each of these signals will determine only the speed with which the changes occur between points.
In the receiver the detector, or demodulator, must be capable of restoring the frequency variations to their corresponding audio-amplitude fluctuations.
[2. As far as the ear is concerned, it makes no difference whether an increase in signal voltage results in an increase or decrease in carrier frequency. The important point is that a large modulating signal results in a large variation of frequency. At the receiver, the ear responds primarily to the different amplitude changes (and frequency changes) of the audio signal and not to their phase. This is due to the relative inability of the ear to respond to phase shifts. ]
Demodulation, as its name suggests, is the reverse of modulation. In FM receivers, some circuit is needed which will give a large output for a large frequency deviation from the resting frequency and a small output for a small frequency variation. This is the task of the FM detector. How this job is accomplished will be described in detail in Section 9. For the present, of greater concern is what happens and this we have just learned.
It is simple to deduce that in FM the signal will occupy a large bandwidth, since the primary purpose of the modulating audio signal is to vary the carrier frequency. In amplitude modulation, it will be recalled, the amplitude of the carrier was varied, and from this a frequency spread (side bands) was created. AM sidebands are not easily visualized and only by resort to mathematics or by direct experimentation can they be shown to exist. The maximum degree of amplitude modulation that can be applied to an AM wave without producing distortion is limited to a value equal in amplitude to the carrier wave. This is defined as 100 percent modulation.
For the FM system, the term "100 percent modulation" is much more arbitrary and the limits to which a carrier can be frequency-modulated ex tends far beyond those presently utilized.
It is known, from theoretical considerations, that we can alter the frequency of a carrier only to the point where we do not, so to speak, obliterate it. Consider a carrier of 90 mhz which is being modulated. We can shift the carrier frequency only until it is brought to zero; anything less is impossible since negative frequencies do not exist. Engineering limitations prevent us from introducing this large a shift, but even if it were possible, it would still be undesirable because of the limitation imposed by the number of commercial stations that could be licensed. Recognizing these difficulties and concerned with the problem of accommodating many stations in the avail able radio spectrum, the F.C.C. has decreed that the maximum deviation through which the carrier may be shifted shall be limited to ±75 khz during modulation. This may be designated arbitrarily as 100 percent modulation, although it must be remembered upon what limitations this value is founded.
As a comparison with AM, it is to be noted that when a carrier is completely or 100 percent modulated, its amplitude varies periodically between zero and twice the normal carrier value. Within this limitation, the modulation does not produce distortion. Any modulation greater than 100 percent would definitely produce a distorted output, as shown in Fig. l.2C. In FM, we could, if we wished, shift the carrier far beyond the arbitrarily defined limit of 75 khz and still introduce no distortion. Again we see that the term "100 percent modulation" does not apply to FM in the same sense that it does to AM. However, from certain considerations that will be developed later, the value of 75 khz is satisfactory. In addition, to diminish the effects of overlapping, an additional 25 khz is allotted as a means of protection between stations operating on adjacent frequencies. Each station, then, is as signed a bandwidth of 200 khz. Of this 200- khz bandwidth, 150 (±75) khz is to be employed for the modulation and the remaining 50 (±25) khz is to function as a guard band. The very definite need for the guardbands will become more apparent after a closer study of the FM sidebands.
FM Sidebands. Before we approach the somewhat complex subject of the sideband frequencies generated in FM, let us pause and quickly review the situation from the AM angle. We have noted that sideband frequencies were not present until an audio signal was applied. The carrier wave independently has no sideband frequencies. Upon the application of a modulating voltage, say of one frequency, two sidebands were formed. Their frequencies were above and below the carrier by an amount equal to the modulating frequency. Throughout this process of modulation, the carrier power remained unchanged, the sidebands deriving their power from the audio signal.
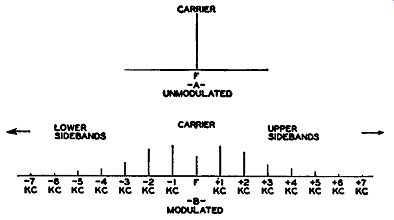
Fig. 1.5. An FM signal with its sidebands developed as a result of audio
modulation.
Now let us look at the FM situation. Upon the application of a sine wave modulating signal, the carrier frequency is shifted back and forth, from a maximum position above the carrier frequency to a minimum position below. And in the process of shifting, additional sidebands are formed, with frequencies intermediate and beyond the maximum and minimum points reached by the carrier. In fact, theoretically, the sidebands are infinite, stretching away on either side of the carrier center position in equal number.
If we attempt to illustrate the sidebands with a diagram, we obtain the result shown in Fig. 1.5B. Fig. 1.5A represents the carrier before the modulation is applied. Fig. 1.5B reveals considerable information regarding FM and helps to answer the confusing problem arising from the statement that infinite number of sidebands are present when a carrier is modulated by an audio signal. But, you may ask, if we have an infinite number of sidebands, how is it possible to have more than one station on the air, at any one time? Upon examination of Fig. 1.5B, we can count seven sideband frequencies below the carrier and seven sideband frequencies above the carrier, all due to the single modulating note. Each of these frequencies, it can be mathematically shown, is separated from its neighbor by an amount equal to the frequency of the modulating signal itself. Thus, if we whistle a 1000-cycle note into a microphone, a series of sidebands appear, above and below the central resting point, each 1 khz (1000 cycles) apart. With the carrier situated at 90 mhz, there would be sidebands at 90.001 mhz, 90.002 mhz, 90.003 mhz, etc.; also sidebands at 89.999 mhz, 89,998 mhz, 89.997 mhz, etc. It is thus clearly indicated that the frequency of the modulating audio signal accomplishes two things:
1. Fixes the separation of the sidebands.
2. Determines the rapidity with which the sideband distribution changes.
Returning to Fig. 1.5B, we can count but fourteen sidebands in all: seven above the carrier, seven below. Apparently this is a misrepresentation, since a moment ago it was stated that there exists an infinite number of these side bands. Actually, both statements are reconcilable; for one condition represents the theoretical condition, and the other the practical modification.
With any strength of modulating voltage, we will find a certain number of sidebands generated which have sufficient power to be of value toward the reception of that signal. Beyond this, additional sidebands exist but contain so little power as to be of no practical importance in the formation of the signal at the receiver.
Here, then, is the reason why more than one station can operate at any time. The sidebands of the other stations are so weak beyond their band limits that, so far as interference is concerned, they are without effect. Included, too, is the answer for the establishment of guardbands about each station. Each station is limited to 75 khz on each side of its carrier frequency, but we know from theoretical considerations that additional side bands exist. Hence, to be absolutely certain that no interference will be caused to adjacent stations, the 25- khz guardband (at each band end) is added. In AM no such complications arise, and consequently there is no need for such precautions.
Sideband Power. Let us return again to a study of Fig. 1.5B. If we compare the amplitudes of the several sidebands with each other and with the carrier, we are at once struck with two facts: first, we find that the carrier power diminishes during modulation; second, it is possible for one or more sidebands actually to contain more power than the carrier.
The power that is taken from the carrier, during modulation, is distributed among the various sidebands. The louder the modulating signal, the greater the energy that will be taken from the carrier. In fact, it is perfectly possible for the carrier, during one of these modulation sweeps, to contain no energy at all; the sidebands then possess it all. A moment's reflection should show that a transfer of some or all of the original carrier energy to the sidebands must occur, because the total frequency-modulated signal does not vary in amplitude. Thus, the only way to satisfy this condition, during modulation, is to transfer part ( or all) of the carrier energy to the sidebands. This power transfer is a characteristic of frequency modulation.
The sum of the amplitudes of the sidebands plus that of the carrier gives the value of the unmodulated carrier, provided the addition is performed vectorially. This has special significance because not all the sideband amplitudes have the same polarity at one time. Counting from the carrier, in either direction, we find that all the odd-numbered sidebands have opposite polarity. The even-numbered ones have the same polarity. But, in any case, correspondingly placed sidebands ( with respect to the carrier) have the same amplitude. A simple example will make this clear.
With a carrier situated at 90 mhz and a modulating frequency of 1000 cycles (or 1 khz), we have sidebands at 90.001 mhz, 90.002 mhz, 90.003 mhz, etc.; also sidebands at 89.999 mhz, 89.998 mhz, 89.997 mhz, etc. Counting away from the carrier, in the first set of sidebands, at 90.001 mhz and 89.999 mhz, both frequencies would possess equal amplitudes but would be of opposite polarity.
The next or second set of sidebands would be at 90.002 mhz and 89.998 me; these frequencies also would be equal in amplitude and would have the same sign. Of course, although each set would have the same amplitude, different sets would differ from one another.
This difference is mentioned because the arithmetic addition of the amplitude of the different sidebands of Fig. 1.5B, together with that of the carrier, will not give the same value as the unmodulated carrier. If the diagram of Fig. 1.5B were drawn up with strict regard for polarity, some of the sidebands would have to be drawn below the reference line. That they were not is due to the fact that, as far as this discussion extends, it makes no essential difference. We are interested only in the frequencies generated by modulation and in their distribution.
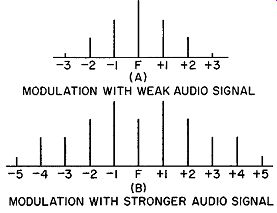
Fig. 1.6. A comparison of the frequency spread of two FM signals modulated
by audio voltages of differing intensity.
Sideband Variation. It would be instructive to see the effect upon sideband distribution when we vary the amplitude of the modulating voltage. This is shown in Fig. 1.6. It is apparent that, as we increase the intensity of the audio signal, the number of significant sidebands increases. The sidebands of the low-intensity modulating voltage that were considered negligible now gain enough power to make them significant. The energy is spreading out, creating more side bands of appreciable power and thereby causing a greater overall frequency spread about the carrier. This is what we mean when we say that the louder the modulating signal, the greater our carrier will deviate from its mean position. At low modulating intensities, the important sidebands are clustered about the carrier. As we raise the volume, the energy spreads out and more sidebands must be included.
It is now possible to replace the elementary explanation regarding frequency spread given at first with the more accurate discussion given above.
We see that the shifting of the energy of an FM wave is directly related to the intensity of the applied audio signal. When a shift takes place, say away from the carrier, the former energy distribution is replaced by this newer arrangement, with every sideband and the carrier affected. Thus, energy is taken by some and given up by others. The total energy, however, under all conditions, remains constant.
Modulation Index. With an appreciation of the relationships between modulating signal strength and sideband formation, we can more easily approach the problem of designing networks to receive and pass the necessary band of frequencies. It is quite evident that if we limit the amplitude of the modulating signals we control the spread of significant sidebands and thus prevent any interference to adjacent channels. The limit set by the F.C.C. is plus and minus 75 khz about the frequency of the carrier. Steps must be taken, at the transmitter, to see that these limits are not exceeded. But is the strength of the audio signal the only determining factor in bandwidth spread? Or must we add another factor? Let us see.
It has been noted that, whenever sidebands are formed, they are spaced by an amount equal to the frequency of the modulating audio signal. Thus, for an audio voltage with a frequency of 100 cycles, successive sidebands are created 100 cycles apart, whereas, for a frequency of 15,000 cycles, the side bands are spaced at intervals of 15 khz. However, if the two signals are causing 10 important sidebands about the carrier, the 100-cycle note would result in an FM signal with a spread of 10 X 100 or 1000 cycles (1 khz) and a total bandwidth of 2 khz. With the 15- khz note, the total frequency spectrum would extend 300 khz. The obvious conclusion from this illustration is that the frequency bandwidth required by a frequency-modulated carrier depends upon two factors:
1. The intensity of the applied modulating voltage.
2. The frequency of this voltage.
Recognition of the importance of both these considerations has led to the formation of the modulation index, which is defined as:
deviation of FM carrier / audio frequency causing this deviation
... where the deviation of the FM carrier is a direct result of the intensity of the applied signal.
We note from this formula that, if the frequency of a signal is kept constant, the bandspread about the carrier will depend directly upon the strength of the modulating voltage; whereas if the sound amplitude is kept constant, the lower audio frequencies will produce more sidebands. In practice, how ever, neither one is kept constant and both vary simultaneously.
The spread of any FM signal will depend upon the modulation index.
At the present time, the F.C.C. has specified that the maximum shift of an FM carrier should be limited to 75 khz. The highest audio modulating frequency in use is 15,000 cycles. The ratio of these two maximum quantities, according to the modulation index, is 75 khz/15 khz, or 5. This figure, besides being known as the modulation index, is also assigned the special name of deviation ratio. The reason for designating this one case as the deviation ratio is that any other combination of audio frequency to carrier shift less than the maximum values will always produce a narrower signal spread. This will be seen as we progress.
Index Table. Taken by itself, the index figure does not directly tell us anything. But, when applied to appropriate mathematical tables derived from Bessel functions, we can obtain the number of significant sidebands that will be formed at this particular value of modulation index.
A knowledge of Bessel functions is not specifically required in order to use the tables derived from these equations. Because of the complexity of Bessel equations, it is convenient merely to accept the tables without proof. A modified version sufficient for our discussion is given in Table I. Full inclusion of all possible values would fill many pages and add very little to what we can learn from the condensed version of Table I. In Table I there is a list of the number of significant sidebands that would be obtained for some of the common values of the modulation index.
Thus, with an index of 5, there are 8 important sidebands (on either side of the carrier) formed; with an index of 10, the number of sidebands increase to 14. For each value of index a certain number of significant sidebands are formed. In general, both vary directly. A large index results in a large number of sidebands; a small index, a smaller number of sidebands. It is interesting to note that when the index becomes very small, of the order of 0.4 or less, only 2 sidebands are formed, similar to AM operation when one modulating frequency is employed.
INTRODUCTION TO FREQUENCY MODULATION TABLE 1: Modulation Index Number of Significant Bandwidth Required Sidebands (f = frequency of audio signal)
To compute the bandwidth required for each modulation index, simply multiply the frequency of the audio-modulating signal by twice the number of sidebands given for the modulation index. Thus, suppose we have a modulation index of 5 when the audio frequency is 5000 cycles, or 5 khz. From Table I, a modulation index of 5 gives us 8 important significant sidebands, each, in this case, to be situated 5 khz apart; thus, 5 khz X 8 = 40 khz on each side of the carrier, or a total bandspread of 80 khz.
It is always completely puzzling to anyone approaching FM for the first time to learn that, although the carrier frequency in the FM transmitter is never actually shifted beyond the ±75 khz limits specified by the F.C.C., sidebands do appear beyond these limits. As an illustration, consider the case when the modulation index is 5, obtained by shifting the carrier ±75 khz with a 15,000 cycle audio note. From Table I we see that 8 significant side bands will be obtained. This, of course, means 8 above and 8 below the carrier position. Since each sideband is separated from its neighbor by 15,000 cycles, or 15 khz, we find that the total required bandwidth is
2 X 15 khz X 8 = 240 khz
Thus we obtain a signal extending over 240 khz (±120 khz) when the carrier frequency is shifted only ±75 khz in the transmitter during the process of modulation.
To explain this situation physically, we might use the analogy of a man moving his finger back and forth at the center of a small pool of water. We know from actual experience that, although the man may move his finger only slightly back and forth, water ripples will appear far beyond this little area. The greater the distance covered by the man's moving finger, the greater the spread of the water ripples. In FM, the greater the carrier swing, the greater the number of sidebands obtained.
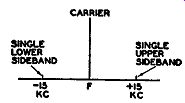
Fig. 1.7. The sideband distribution when the modulation index is small,
0.2 or less.
In commercial practice, it seldom happens that a 15- khz note will have sufficient volume to spread the transmitter carrier to the 75- khz limits.
As the frequency of the signal is lowered, the number of sidebands that extend beyond the ±75- khz limits also decreases, until at 50 cycles a full carrier swing will just produce sidebands up to, but not beyond, the 75- khz limits. Here, then, is the reason for the additional ±25- khz guard bands. They tend to absorb any sidebands that extend outside the 75- khz limits.
Many incorrect interpretations have been placed upon the F.C.C. regulation that, during modulation, the carrier is not to be shifted more than ±75 khz. This does not mean, for example, that the end significant sideband must not extend beyond ±75 khz. It merely means that during the process of modulation, when the carrier frequency is being altered by the applied audio voltage, the maximum shift be no greater than ±75 khz. However, when the full 75- khz shift is utilized, it will generally be found that significant sidebands exist beyond the F.C.C. limits. This is perfectly permissible.
When the carrier swing is very small, 0.4 or less for the modulation index, then Table I reveals that only 2 sidebands ( one above and one below the carrier) are obtained. If the audio-modulating signal is 15 khz, then a modulation index of 0.2 means that the carrier frequency is only shifted 3 khz back and forth.
AF o.2=T AF = 15 khz x 0.2 AF= 3 khz
The frequency distribution will appear as shown in Fig. 1.7, with one carrier and two significant sidebands.
Note again that the sidebands will be spread farther from the center than the frequency shift that produced them. The sidebands are ±15 khz from the center, whereas the carrier was shifted only ±3 khz. This situation will be generally true of all FM transmissions. However, if the reader remembers the water analogy, it may help him to understand this new idea.
We have, up to this point, a fairly complete picture of FM, both before and during modulation. Of remaining interest is phase modulation, not only because it represents a very possible method of sending intelligence but, more important from our viewpoint, because phase modulation indirectly results in FM .. The latter aspect is all the more important because interference affects an FM signal through its phase disturbances. Moreover, phase shifting is employed in commercial transmitters to produce FM. To appreciate either of these two aspects, a brief discussion of phase modulation is necessary.
EXAM
1. What effect does the choice of the high frequencies to transmit FM signals have on the ability of FM to override interference? What would be its effect if AM was used at the same frequencies?
2. What is the significance of 100 percent modulation when applied to AM broadcasting? Explain its counterpart in FM.
3. In an AM wave, where is the intelligence contained? How does this differ from the conditions prevailing in frequency modulation?
4. What is the relationship between the sidebands produced in amplitude modulation and the audio-modulating frequency?
5. Is the carrier frequency actually shifted when a wave is frequency-modulated? What is the F.C.C. regulation in this regard?
6. What is a discriminator? What is the accepted application of this word?
7. What are guardbands and why are they required in FM transmission?
8. Discuss the difference between the sidebands produced through amplitude modulation and those produced by frequency modulation.
9. What do we mean when we refer to a sideband as being "significant"?
10. What influence does the audio-modulating signal frequency have in the production of an FM signal?
11. Where do the FM sidebands obtain their power? Contrast this with the situation existing in an AM signal.
12. Explain how the sidebands vary, both in power and number, during different portions of an audio-modulating cycle.
13. The F.C.C. specifically limits carrier shifting to ±75 khz. Can sidebands ex tend beyond these limits? Explain, using a numerical example.
14. Explain the importance of the modulation index.
15. With a modulation index of 3 and a modulating frequency of 5 khz, compute the complete bandwidth required when a 90 -mhz carrier is employed.
16. Analysis of an FM signal revealed that the carrier frequency was 94 mhz, and the upper and lower sideband limits were at ±98 khz. Further analysis indicated that the modulating frequency was 14 khz. What modulation index was being employed at the transmitter?
17. Under what conditions are the bandwidths of FM and AM signals exactly equal to each other?
18. The F.C.C. specifies that the modulation index, with a 15,000-cycle modulating frequency, shall not exceed 5. Assuming that the amplitude of the modulating: signal remains constant, what happens to the modulation index when the audio frequency is reduced? Docs the bandwidth increase or decrease as we lower the audio frequency? Illustrate your answer by computing the bandwidth required for audio modulating frequency of 12 khz, 9.375 khz, and 7.5 khz.
19. A sideband is considered insignificant when it contains less than 1 percent of the total carrier power. Express this in terms of db.
20. Does a signal with a large modulation index necessarily require a wider band width than a second signal having a smaller index? Explain your answer.
+++++++++++