Up to this point we have discussed in general the differences be tween the FM, the p-m, and the a-m waves. A fair understanding of what an FM and a p-m wave looks like in comparison with an a-m wave has been obtained. We are now ready for a discussion of how FM and p-m waves are produced. An analysis of FM and p-m transmitters will be made in this Section. The basic principles of how an FM transmitter works and the fundamental circuit analysis will be included, rather than design problems. The sections of the FM transmitter that will be stressed are those dealing primarily with the production of FM signals.
As with AM, there are numerous methods of producing the final FM and p-m signals, and we will study the systems that are most common. The intention of this Section is to cover as much material relative to the operation of the transmitters as is necessary fully to understand this operation.
The Basic Transmitter
In the first Section, block diagrams of typical FM and p-m transmitters were illustrated, together with the block diagram for a typical a-m transmitter for comparison purposes (see Fig. 1-14). The most important section of the FM and p-m transmitters that differed appreciably from the a-m transmitter was the modulator system. There fore, the modulator sections of the FM and p-m transmitter will receive the greatest consideration. In FM the modulated signal is achieved somewhere at the beginning of the transmitter (that is, at the low power-level stages.) In AM, especially high level trans mission, the modulation is performed somewhere at the output stages of the transmitter after the frequency multiplication stages. In FM the modulation is performed before the frequency multiplication stages because the frequency multiplication aids in increasing phase shift and frequency deviation, besides effectively increasing the carrier frequency,
To effect a change of frequency in the carrier of the direct FM type of transmitter, a reactance tube modulator or some similar circuit is almost invariably used. This reactance tube works in conjunction with the audio signal to produce a variable reactance across its output. This variable reactance can be either inductive or capacitive in character. If this variable reactance is placed across a tuned LC tank circuit, the effective inductance or capacitance of the tank circuit will change, which in turn will change the resonant frequency of the tank circuit, since the resonant frequency is dependent upon the effective values of L and C. This will be evident when reactance tubes and reactance tube modulators are studied in greater detail in the forthcoming sections. These reactance tubes usually work directly with the oscillator of the FM transmitter for purposes which will be evident later. The oscillator circuits themselves are similar to those employed in a-m transmitters where crystal control is not used.
For indirect FM (or p.m.) the situation is somewhat different, in that it is the phase of the signal that is varied directly and not the frequency. For this reason practically all types of indirect FM or p-m transmitters use crystal oscillators as compared with the non-crystal (inductance-capacitance) oscillators employed in direct FM transmitters. There are numerous methods of producing a p-m signal, but in this Section only one p-m system will be discussed in detail. In the following Section a number of FM transmitters in use today will be analyzed, and included among them will be three different methods of producing a p-m signal.
The preceding two Sections mentioned certain standards and relationships between the carrier frequency and the audio modulating frequency which pertain to the requirements for proper FM trans mission. Such topics as the maximum amount of frequency deviation, obtaining the correct frequency of transmission, and acquiring of the necessary amount of phase shift to give the required amount of phase deviation for p.m. were referred to, but the methods of securing these requirements were not discussed. In the ensuing sections of this Section the topics of modulation and frequency multiplication will be of great benefit, in that they will indicate the methods of obtaining these necessary requisites for the proper operation of FM and p-m transmitters.
Whether or not the FM transmitter is designed to work on a relatively high power output, the basic considerations as mentioned above are the same. The basic transmitter design of the oscillators, modulators, afc circuits, and frequency multipliers are relatively the same as far as principle or operation is concerned. Whatever fundamental considerations hold for one type will generally hold for similar types.
Simple Frequency Modulator
Frequency modulators had been used long before FM transmitters were in commercial use. Anyone familiar with visual methods of aligning a-m receivers will recall that frequency modulators, commonly known as wobbulators, are used in conjunction with oscilloscopes, to align the i.f.'s by obtaining the correct selectivity or resonance curves on the oscilloscope. The principle underlying the operation of most types of wobbulators is very simple. In effect its basic operation is as follows: The rotor of a variable air capacitor is revolved past its stator by an electric motor. This capacitor is connected to the oscillating circuit of a signal generator such that the variable capacitor varies the capacitance of the circuit at values determined by the degree of rotation.
The frequency of rotation of the capacitor determines how many times per second there is a cyclic repetition of the complete capacitance change. With arrangements of this kind, the total bandwidth covered may be from a very few percent to perhaps ten percent of the mean frequency. The amplitude of the wave is fairly constant over the entire range, and the speed of rotation represents the audio frequency, or the time rate of change in frequency. The item of audio amplitude which would determine the amount of frequency deviation does not enter into this operation.
Frequency modulators that inject variable reactances into tuned circuits as used in the transmitters today are known as reactance tubes. The analysis of reactance tubes will be discussed at greater length in the following section. In this section we will study a circuit that is one of the simplest types of frequency modulators in order to illustrate basically how a signal can be frequency modulated. After this analysis, it will be much easier to understand the functioning of a reactance tube as applied to the topic in question.
For the moment, before introducing the simple type of frequency modulator, let us refer to an elementary theoretical type of amplitude modulator. We know that to amplitude modulate a carrier, the instantaneous amplitude of the carrier is varied in accordance with the varying amplitude of the audio modulating signal. If a resistance is introduced into an oscillator circuit (in series with the tank coil and capacitor), the resistance will introduce a loss and the over-all amplitude of the oscillatory signal will be reduced according to the value of the resistance. If this new reduced signal is considered as the carrier and if the resistance is made variable above and below its original value, then the amplitude of the carrier will vary accordingly.
In other words, when the value of the resistance is increased, there will be a greater loss in the circuit, and the amplitude of the carrier will decrease. Likewise, if the value of resistance decreases, there will be less loss and the amplitude of the carrier will be increased. If this resistance is made to vary at an audio rate, the amplitude of the carrier also will vary at the same audio rate, and the carrier then will be amplitude modulated. This type of a-m wave can be very simply attained by placing in series with an LC tank circuit some type of resistance which will vary at audio rate.
The question then arises as to what this resistance can be. The answer is very simple - a carbon microphone. This microphone contains finely divided carbon granules placed between two conducting disks.
One disk is fastened to part of the mike while the other disk is fastened to a movable diaphragm plate. When the plate is at rest, these granules provide an electrical path, exhibiting a certain amount of resistance, between the disks. If the pressure between the two solid carbon plates is varied, the pressure upon the loosely packed carbon granules is also varied. The resistance of the electrical path through these granules changes upon application of pressure to them, and consequently their resistance changes with the application of sound waves to the diaphragm. That is, when sound waves strike the diaphragm, causing it to vibrate in accordance with the frequency of the audio, the pressure upon the carbon granules changes, which in turn changes the resistance of the electrical path they provide between the disks.
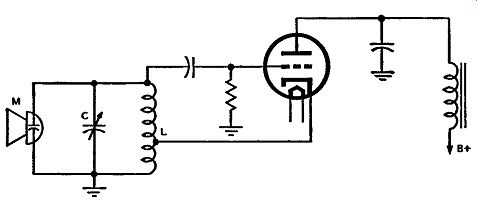
Fig. 3-1. The frequency of the oscillator tank circuit can be changed
by actuating the condenser microphone M; this is a type of simple frequency
modulator.
To show the operation of a simple frequency modulator circuit, an analysis similar to the foregoing will be illustrated. Instead of using a carbon microphone as the varying element, a condenser microphone is used. Bearing in mind the possibility of varying the frequency of a tuned oscillator circuit by changing either the capacitance or the inductance, we can proceed with the discussion of what is actually the simplest type of frequency modulator resembling the operation of a broadcast transmitter. This is shown in Fig. 3-1, wherein a condenser type microphone M is shunted directly across the tank circuit ( capacitor C and inductance L) of a simple Hartley oscillator circuit. This circuit is not intended to convey the idea that this is the type of oscillating system actually used in the transmitter, or that which we shall describe is the exact method of producing the FM signal. How ever, if you appreciate that the frequency of an oscillating system can be varied by changing the tuning capacitor - then the arrangement as shown will be productive of information concerning not only the generation of an . FM wave, but also the relation between the audio modulating voltage, the frequency of this voltage, and the FM carrier. Before going into the analysis of the circuit of Fig. 3-1 let us understand how the condenser microphone works.

Fig. 3-2. The movable diaphragm of a con denser microphone is vibrated
by sound waves and this action varies the distance be tween the diaphragm
and the fixed plate, providing a varying capacitance between the two
plates, as at A and B.
Fig. 3-2 illustrates a simple diagram of a condenser microphone. It essentially consists of two metal plates separated by insulating spacers so that each plate acts as a part of a parallel plate capacitor. One of these plates (a heavy one) is fixed in position within the mike and the other is a very thin plate in the form of a diaphragm. This latter plate has the ability to vibrate upon application of a variable air pres sure (sound wave). Since the effective capacitance of a parallel plate capacitor is directly dependent upon the common area between the plates and inversely dependent upon the distance between the plates, it can readily be conceived that the capacitance between these two plates will vary if the movable diaphragm vibrates.
For instance, if a sound wave that is applied to the microphone causes the diaphragm to move outward (that is, away from the fixed plate) the distance between the two plates is effectively increased and the capacitance decreased. On the other hand, if a sound wave causes the diaphragm to move inward (that is, towards the fixed plate) the distance between the two plates is effectively decreased and the capacitance increased. A vibrating or to-and-fro motion of the diaphragm is a natural action when sound is applied to the microphone. It is quite easy to see how the change in position of the diaphragm changes the effective capacitance between the two plates. If each plate had a lead connected to it, a variable capacitance would appear between these two output leads in accordance with a variable sound input to the microphone.
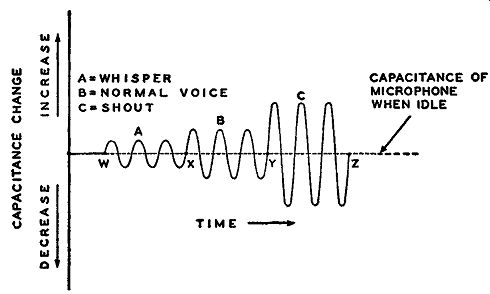
Fig. 3-3. The greater the intensity of the impinging sound of the same
frequency on the diaphragm of a condenser microphone, the greater is
the change in the output capacitance.
The very interesting detail in the analysis of a condenser microphone that makes it useful as a means of introducing a method of frequency modulation is the manner in which its capacitance changes in accordance with an audio signal. There are two characteristics of on audio signal that affect the diaphragm of the microphone. One is the volume or level of the signal, and the other is the frequency of the signal. Tr..e greater the volume intensity of the audio signal, the greater will be the sound pressure on the diaphragm and the greater the variation of the diaphragm. Hence, a larger change in the effective capacitance exists across the output leads A and B. The way the capacitance of the microphone changes with the intensity of sound is illustrated in Fig. 3-3. In this figure the change in microphone capacitance is indicated for three sounds of the same frequency but of different intensities, such as the equivalent of a whisper, a normal speaking voice, and a shout. The exact change in capacitance is not important at this moment. The frequency of these signals is the same, as indicated by the time references between points wand x, x and y, y and z, all being equal to each other.
The other characteristic of the audio signal, namely its frequency, does not affect the distance that the microphone diaphragm moves, but it does affect the number of times a second that this change in capacitance takes place. This is analogous to the wobbulator, wherein the speed of the motor determines how many times a second the change in capacitance, caused by the rotating capacitor, takes place.
If the period of time between points w and x of Fig. 3-3 is equal to 1 second, the number of cycles involved in that period of time due to a whisper is equal to 3 cycles per second. (This is evidenced by counting the number of completed cycles in that period of time.) If the intensity of sound of the whisper were to remain the same while the frequency increased to double its value, or 6 cycles per second, then for the same period of time between w and x, there would be 6 cycles completed, but the amplitude of the signal, or the change in capacitance would be the same.
Let us now refer back to the oscillator circuit of Fig. 3-1. With no sound going into the microphone the diaphragm is at rest, and the effective capacitance of the oscillator circuit essentially consists of the capacitance C in parallel with that of the microphone. This effective capacitance in conjunction with the inductance of L determines at what frequency the tuned circuit will oscillate. This frequency is termed the resting or carrier frequency of the circuit. With the micro phone capacitance in parallel with the tuned circuit of the oscillator, it is evident that any sound waves impressed on the diaphragm of the microphone will be translated into capacitance variations and that these, in turn, will vary the resting frequency of the oscillator tuned circuit.
The greater the change in microphone capacitance, the greater will be the change in the circuit capacitance -- hence the greater will be the change in frequency of the oscillations developed in the oscillating circuit. As can be interpreted from the capacitance change in Fig. 3-3, this change in .frequency takes place on both sides of the so-called "resting" or "idle" microphone frequency which is the unmodulated carrier frequency. Thus, we might say that a tone which has the intensity or amplitude of a low speaking voice might change the frequency of the oscillator by ±2 khz; an amplitude equivalent to a moderate voice might change the frequency by ±4 khz; and an amplitude equivalent to a loud voice might change the frequency by +6 khz.
What happens when the frequency of the sound changes? It varies the rate at which the frequency of the oscillating circuit is changed.
The higher the frequency of the sound waves, the greater the number of times per second the oscillator frequency will be altered. If a 1000 cycle tone of a certain loudness will change the frequency of the oscillator by 40 khz both sides of the carrier 1000 times per second, a 4000-cycle tone of the same loudness will change the frequency of the oscillator by 40 khz, 4000 times per second, and a 200-cycle tone of like loudness will change the frequency of the oscillator by 40 khz, 200 times per second. Thus the arrangement shown in Fig. 3-1 satisfies the basic requirements of an FM transmitter, in that the amplitude of the audio signal varies the frequency of the carrier ( that is, determines its deviation) and the frequency of the audio determines how many times a second this deviation takes place.
From what has been discussed relative to the formation of an FM signal, the general structure of an FM wave as indicated in the first two Sections can be readily understood.
Returning again to the means of producing frequency-modulated waves, the condenser microphone arrangement shown in Fig. 3-1 has its drawbacks. The fact that it is restricted to the use of a condenser type microphone is an undesirable feature when so many other types of microphones are in use. Furthermore, it is often necessary to separate the microphone from the FM transmitter by considerable distances; this arrangement is impossible if the circuit of Fig. 3-1 is used.
Consequently, some arrangement is required with which any type of microphone can be used and wherein a convenient separation of the microphone and transmitter will be possible. Such an arrangement is found in the use of a reactance tube.
Reactance Tubes
Before we discuss some actual frequency modulator circuits that make use of vacuum tubes as a means of producing a signal varying in frequency, it will be necessary to analyze the basic type of tube circuit that causes this variation. This type of tube circuit is known as a reactance tube circuit. In terms of practicality, if we can design a circuit so that a vacuum tube receives the audio signal output from a microphone and, due to the frequency and amplitude variations of this audio signal, injects varying reactances into accompanying oscillatory circuits, then we have a method of frequency modulation. This vacuum tube, which is called a reactance tube as previously mentioned, functions typically, but its circuit arrangement is so designed that by varying the degree of grid bias the output impedance of the circuit varies, this variation being principally reactive.
As a basis for analysis of a reactance tube circuit, some factors relative to amplifying vacuum tubes should be understood. These are the three basic tube constants which are the transconductance or gm of the tube, the amplification factor or µ (mu) of the tube, and the dynamic plate resistance or rP. An exact understanding of what is meant by these three tube characteristics is essential to the complete comprehension of what is to follow in regard to reactance tubes.
The transconductance, gm ( or mutual conductance as it is sometimes called) of a tube is defined as the ratio of the change in plate current, ib, to the change in grid voltage, ec, which produced it, this ratio being considered with the plate voltage, eb, remaining constant.
Symbolically it is written as gm= ddib •••• • (with eb constant); ec
In this ratio the letter d means a "change in." Since the plate cur rent, expressed in amperes, is in the numerator and the grid voltage in the denominator of this ratio, the gm is expressed in units called mhos. (In other words, mhos is the reciprocal of ohms.) There are other trans-conductances between certain other elements of a tube but with these we are not concerned. When the term transconductance is used without qualification, it is always the control-grid to plate trans conductance that is meant, and the usual symbol is gm. It is a known fact that a change in the grid voltage of a tube causes a change in the plate current of the tube especially with the plate voltage remaining constant. These changes do not occur in such a fashion that gm is kept constant. With the change in plate current caused by the change in grid voltage the gm of the tube also changes and does not remain constant but rather varies over wide limits depending upon the point of operation. In practice the trend in expressing the gm is toward the use of micromhos (millionths of a mho) in order to avoid the use of decimals. The transconductance, gm, is a very important property of a tube, because it tells how effective the grid is in effecting a change in the plate current of the tube, and this is very important in the analysis of reactance tubes, as will be seen.
The amplification factor, µ, or amplification constant, expresses numerically how much greater effect on the space charge the electro static field set up by a voltage applied to the grid has than the electro static field set up at the plate by the same voltage. This is a numerical expression which is based upon the action of the grid and plate fields upon the space charge with respect to the distance between the grid and plate. By definition, amplification factor,µ, is the ratio between a small change in plate voltage and a small change in grid voltage while the plate current remains unchanged. Otherwise expressed,
µ = ddeb ••••• (ib constant)
ec
However, if the changes are appreciably large, then the plate cur rent will also change. In which case, in order for the definition to hold, the change in plate voltage and the change in grid voltage both should produce the same change in plate current independently. It requires a much greater change in plate voltage than in grid voltage to cause the same change in plate current. Thus, a tube may have a "mu" of 10, which means that a change in grid voltage is 10 times as effective in controlling the plate current as the same change in plate voltage.
Reference to amplification occurs in the following manner: with a steady voltage applied to the control grid and a steady voltage applied to the plate, a steady value of current flows in the plate circuit. A variation in the voltage upon the grid, with the voltage applied to the plate of the tube held constant, causes a change in plate current. Since the current in the plate circuit has been varied, the effect is equivalent to a change in the plate voltage, namely, that change which would have produced an equal variation in plate current if the plate voltage had been altered while the grid voltage was held fixed. Because of the greater effectiveness of a change in grid voltage in influencing the plate current, the equivalent change in plate voltage can be considered as equal to the change in grid voltage multiplied by that number which identifies the number of times a change in grid voltage is more effective than a change in plate voltage in influencing the plate current.
Another very important property of vacuum tubes is the dynamic plate resistance, or r, of the tube. This resistance is defined as the ratio between a small change in plate voltage and a small change in plate current with the grid voltage remaining constant. Expressed mathematically, r11 = dd~b- .... (e0 constant)
This relation is particularly important when working with vacuum tube circuits, because it is often desirable to know the resistance of the plate circuit of a tube in comparison with the rest of the circuit in which it is used.
These tube constants for almost all types of tubes can be found in handbooks. Even if they are not given directly, they can be derived from the family of curves usually supplied with good tube handbooks. In most cases only the gm and r,, are listed for pentodes and the µ. and r,, for triodes. The reason for this is that in pentodes the gm is often considered more important than the /L of the tube and vice versa for triodes. However, the other tube characteristics can be determined from the graphical characteristic curves of the individual tube in question.
In passing it may be wise to state that a relation exists among these three tube constants such that:
µ=r.,,g,,. This is proved from the knowledge that deb d deb d
µ= -an rt>= -d. an de0 ib g,,. = dib de
---------------
For a good analysis of determining the values of g,,., µ, and r., from the characteristic curves of the respective tubes; see the book, "Inside the Vacuum Tube," by John F. Rider, John F. Rider Publisher, Inc.
-----------------
.... therefore, substituting the quantities in the above expression we find: deb = deb X dib dee dib dee where the dib's cancel out since they appear in the numerator and denominator of the right side of the equation and, consequently, deb_ deb dee - dee which proves the above relation between the tube constants.
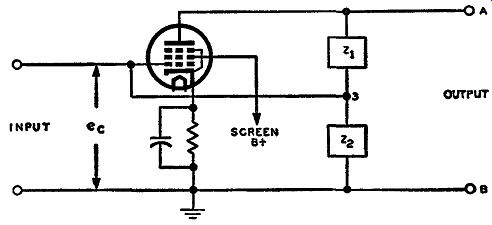
Fig. 3-4. A basic reactance tube circuit. The impedances Z1 and Z.s
can be a combination of resistance and inductance or resistance and capacitance,
but not a combination of inductance and capacitance.
With the basic concept of tube constants established let us return to the discussion of reactance tubes. These tubes had been used long before FM was commercially feasible, primarily in automatic frequency control circuits, which will be discussed later in this Section.
In Fig. 3-4 the basic circuit for a reactance tube is shown. The two impedances Z1 and Z2 that are in the output circuit can be either a combination of resistance and inductance or a combination of resistance and capacitance. In other words there are primarily four possibilities in the combination of Z1 and z,. If Z1 is capacitive, z, is resistive. If Z1 is resistive, Z.s can be either inductive or capacitive. If Z1 is inductive, Z11 is resistive. It will be noted that any combination of inductance and capacitance in the Z1 -Z.s circuit is carefully avoided.
The reason for this is that primarily only a 90-degree phase shift is desired with little or no chance of forming a resonant circuit in the output. This will be evident as the analysis of reactance tubes proceeds.
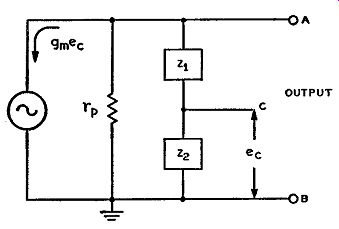
Fig. 3-5. The equivalent circuit of Fig. 3-4 in which the tube can be
considered as a constant current generator with internal resistance equal
to the plate resistance of the tube.
The circuit of Fig. 3-4 can be considered as though a generator was in parallel with the two series impedances of Z1 and z,. When the reactance tube used is either a pentode or a tetrode, the tube can be considered a generator whose generated current ib is equal to gmeo (from the relation Ym = ib/ec) and whose internal impedance is equal to the dynamic plate resistance rp of the tube. Under these circum stances Fig. 3-4 reduces to the equivalent circuit of Fig. 3-5. If the plate resistance of the tube is high (as is usually the case in tetrodes and pentodes) the circuit of Fig. 3-5 can be reduced still further to the equivalent circuit of Fig. 3-6. In this figure the plate resistance and also any other loading resistance is temporarily neglected. If the impedance between points A, B is designated as ZAB and the voltage across points A, B as EAn, then this voltage is equal to the current flowing through the series impedance network of Z1 and Zs multi plied by the impedance between points A, B. The thing we are interested in is the impedance ZAn, because the value of this impedance will indicate to us the value of the injected reactance and resistance that is caused by such a circuit. At first glance it might appear that the output impedance is just the series combination of Z 1 and Zs, especially since the plate resistance of the tube is neglected in Fig. 3-6.
This is not a true picture, because one of the components in the load (Z1 or Z2 ) is reactive, and consequently the injected reactance is a variable factor that depends upon the plate current flowing, as well as the frequency of operation. Since the plate current depends upon the Ym of the tube, the value of the injected impedance likewise depends upon the gm of the reactance tube. This is proved as follows: Impedance ZAB looking into terminals A, B in the direction indicated in Fig. 3-6 is equal to the voltage across A and B divided by the current iAB flowing through Z 1 and Z2. This is nothing more than an application of Ohm's law to alternating currents. (In d-c application Ohm's law states that the resistance R = E/1, whereas in a-c application Ohm's law states the impedance Z = E/1. In the latter case it must be remembered that the phase relationships of a.c. have to be taken into account to obtain a complete answer.)
Therefore, Z,1.B = ~AB (1)
1AB but we know that the current i,1.B is equal to the transconductance multiplied by the grid voltage ec or that i,1.B = gme0 • Substituting this in expression ( 1) gives z EAB (2)
AB=-g e m C
----------

Fig. 3-6. The equivalent circuit of Fig. 3-5, wherein the plate resistance
of the tube is considered sufficiently high to be neglected, as is also
any loading resistance.
----------
In Fig. 3-6 it is noticed the voltage across impedance Zs is the applied grid voltage and this voltage is also equal to a certain amount of the voltage EAB across the whole output network. Here Z1 and Z8 is a voltage dividing network to the voltage EAB. Consequently, the voltage e0 across impedance z, is: E Zi; ec= ABX z +z 1 I (3)
If this value is substituted for e0 in equation (2), Z.tB will be simplified further. Thus ZAe= 22 9m EAe x 21 + 22 Therefore,
= _1_ 9m
(4)
(5)
Equation ( 5) is very important as it tells us what impedance is seen when looking into the reactance tube circuit from terminals A and B. Since the transconductance is given in mhos, 1/gm will be in ohms.
Therefore, equation ( 5) states that the impedance across terminals A and B consists of a resistance in series with a reactance. The value of the series resistance is equal to I/gm, and the value of the reactance is equal to 1/gm X Zi/Z2, where gm is the transconductance of the tube in use and impedances Z1 and z, are, as specified previously, any one of four combinations.
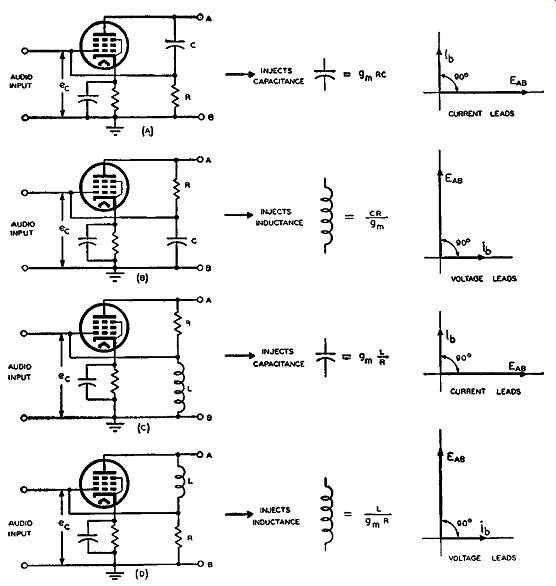
Fig. 3-7. The four possible reactance-tube circuits showing either injected
capacitive or inductive reactances, each of which depends on the value
of the transconductance of the tube. The quadrature phase relations between
the current and voltage are shown in the vector diagrams.
The four possible combinations of these impedances are shown in Fig. 3-7. In part (A) when the impedance Z1 is a capacitance and Zs a resistance, the reactive component of equation (5) [ (1/gm) (Z1 /Z2 )] becomes a capacitive reactance, and the value of the capacitance that is injected into any accompanying circuit is equal to gm RC. The respective injected reactance for the other types of reactance tube circuits is shown in parts (B), (C), and (D) of Fig. 3-7. These injected reactances are based upon the assumption that the impedance in the circuit between the grid and the plate Z1, is much greater (at least 5 times) than impedance Z2. Besides reactances, resistances also are injected, but because of the tubes chosen for reactance tubes in con junction with the accompanying circuits and the fact that Z1 is much greater than Z2, these injected resistances have little effect. For a true picture of what the injected parallel resistance and reactance components are for all four different cases without any assumption as to the magnitude of Z1 compared with Z2, consult Table A in the appendix.
If the injected reactances of Fig. 3-7 are examined, it will be noticed that every one depends upon the value of the transconductance or gm. of the tube. Since the gm of the tube is dependent upon the grid voltage, it is readily evident that, if an audio signal were impressed across the input grid circuit of the tube, the gm of the tube would vary in accordance with the audio voltage variation. Consequently, since the Ym of the tube varies in accordance with the audio input, the injected reactance across terminals A and B, which is dependent upon the gm> will also vary in accordance with the audio.
These reactance tube circuits are often termed quadrature circuits, because there is effectively a 90-degree phase relation between the r-f voltage across terminals A and B in the output and the r-f plate current. When the plate resistance of the reactance tube and the injected parallel resistance are high, both resistances can be considered as having negligible effect on the phase relation between the afore mentioned voltage and current and can be considered as being 90 degrees out of phase: with each other. These phase relations are shown in vector diagrams accompanying each drawing in Fig. 3-7. Where the injected reactance is capacitive, the plate current ib leads the voltage EAB across the output by 90°. This is illustrated in parts (A) and (C) of Fig. 3-7. In parts (B) and (D) the injected reactance is inductive and the voltage output EAB leads the plate current ib by 90°. Let us consider the following as a typical example of how to calculate the injected reactance of a reactance tube circuit. The reactance tubes employed are of the high gm type to provide as high a variation in gm as possible with variation of grid voltage. The reason for this is that the greater the changes in gm that can be accomplished, the greater will be the variation in injected reactance. Consequently, for this example let us consider the circuit of Fig. 3-7 part (A) where the tube used is a 6AC7. With 300 volts on the plate and 150 volts on the screen, the transconductance or gm of the tube for a cathode bias of 2.2 volts is 8000 micromhos. The capacitance used between the plate and control grid is equal to 25 µµf, and the resistance between the cathode and control grid is equal to 1000 ohms. Under these circum stances the injected reactance is capacitive, and the capacitance is equal to the following:
Capacitance = g,,. RC
... and, since gm equals 8000 micro-mhos or 0.008 mho, R equals 1000 ohms, and C equals 25 µ.µ;f, the capacitance equals:
0.008 X 1000 X 25 = 200 µµf
Therefore, 200 µ.µ.f capacitance exists across the output of the circuit with no signal applied to the input. If a sine wave that is alternating one volt above and below the fixed 2.2-volt cathode bias is injected into the grid, the total effective input voltage existing across the grid at the maximum positive peak of audio signal is equal to -2.2 + 1 or -1.2 volts and at the maximum negative peak of audio signal equals -2.2 + (-1) or -3.2 volts. Therefore, the grid bias is alternating between -1.2 volts and -3.2 volts, and the gm also changes. According to the gm curves for the 6AC7, with the previously stipulated voltages applied to the other tube elements, the gm at a grid voltage of -1.2 is equal to 13,500 micromhos or 0.0135 mho, and at a grid voltage of -3.2 volts the gm is equal to about 3800 micro-mhos or 0.0038 mho. Under these limits of grid voltage the injected capacitance will be as follows: For a grid voltage of -1.2 volts and a Ym of 0.0135 mho the injected capacitance = 0.0135 X CR
= 0.0135 X 25 X 1000
= 337 µ.µ.f
And for a grid voltage of -3.2 volts and a g,,. of 0.0038 mho, the injected capacitance = 0.0038 X CR
= 0.0038 X 25 X 1000
= 95 µµf
From these values it can be readily understood that with a fixed bias of -2.2 volts on the grid and a signal that is varying by one volt positive and negative, the injected capacitance varies between the limits of 337 to 95 µµ;f or through a difference of 242 µµf. This example was chosen merely to show how the audio input voltage changes the injected capacitance of the circuit of part (A) of Fig. 3-7 and does not typify values used in practice.
Reactance Tube Modulator (Frequency Modulator)
The preceding section analyzed the fundamentals of reactance tube circuits at great length. It was shown that a reactance tube circuit can be used to inject either a capacitance or an inductance into any circuit that is across its output (that is, the output usually considered be tween plate and ground or plate and cathode of the reactance tube). With circuits such as were indicated by a typical example, a small change in grid bias can vary the injected reactance quite a bit.
In actual practice, reactance tubes are used as modulators where direct FM and in many instances where indirect FM are required.
As used m direct FM the variable output reactance of a reactance tube is used to vary the frequency of an oscillator circuit so that the output of the oscillator will be frequency modulated. The use of the reactance tube as a frequency modulator is seen best if a typical circuit of a reactance tube modulator is studied.
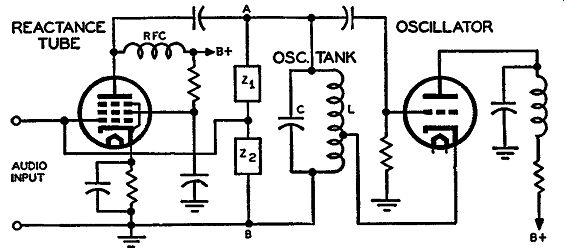
Fig. 3-8. Simplified schematic of a reactance tube modulator (to the
left of terminals A-B) with an oscillator circuit of the Hartley type.
The impedances Z 1 and Z2 can be any of the combinations illustrated
in Fig. 3-7.
Fig. 3-8 illustrates a simplified circuit of a reactance tube modulator in conjunction with an oscillator circuit. The reactance modulator circuit is shown to the left of terminals A and B, and the oscillator circuit to the right of these terminals. The latter is a simple Hartley oscillator in which the capacitance C and the inductance L, in con junction with the reactance injected by the reactance tube, are the components that determine the frequency of oscillations. The reactance tube circuit is illustrated similarly to the way it was in Fig. 3-4 with the impedance Z1 and Z2 shown in the output instead of specific components. This is to avoid limiting the components of Z1 and z, further than to make them any one of the four previous types of combinations.
With no signal voltage applied to the input circuit, the reactance tube will have a fixed value of gm, and according to the values of Z1 and z,, a capacitance or inductance will exist in parallel with the LC oscillator tank circuit. In reality, then, the true frequency of oscillations is determined by the oscillator tank circuit components plus whatever reactance is injected across this tank by the modulator circuit. When no signal is being received by the reactance tube, the frequency of oscillations of the modulator-oscillator is called the center frequency. To understand exactly how the afore-mentioned values control this center frequency let us consider the following: The frequency of oscillations of an ordinary Hartley oscillator circuit, as shown to the right of terminals A and B of Fig. 3-8, is deter- mined by the inductance Land the capacitance C. The frequency fr is called the resonant frequency, and it is determined by the following mathematical relation:
1 fr=---== 2,n/LC ... where L is equal to the inductance in henrys C is equal to the capacitance in farads and 1r is equal to a number whose value is 3.14.
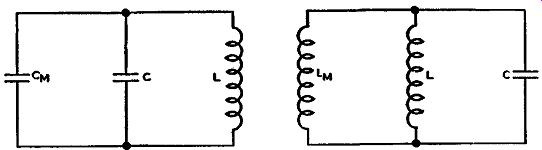
Figs. 3-9, left, 3-10 right. Equivalent circuits of Fig. 3-8 for determination
of the oscillator frequency. In Fig. 3-9 the injected reactance is capacitive,
CM, and in Fig. 3-10 the injected reactance is inductive, designated
as LM.
The mathematical sign under which the product of LC appears is called a square root sign or radical sign ( y'-). The mathematical interpretation of the sign is what number multiplied by itself will give the value of final answer under this radical sign. Thus, a square root sign such as y 12 X 6 is equal to y 72 (first carrying out the arithmetic under the radical sign) and the next question that follows is what number multiplied by itself will give an answer equal to 72.
This number is found to be 8.48.
Therefore, y 12 X 6 = y 72 = 8.48.
However, with the oscillator circuit used in conjunction with the reactance tube modulator, the components that determine the frequency of oscillations are changed. In other words, existing across the LC tank circuit is a fixed value of either capacitance or inductance which is injected across this tank from the reactance tube output when no audio signal is being received. If the injected reactance is capacitive, there are effectively two capacitors in parallel with an inductance, both of which are the determining elements of a new oscillator frequency. The frequency of oscillations is determined by the circuit, as illustrated in Fig. 3-9. The frequency is still dependent upon capacitance and inductance, but the capacitance is changed and equal to the capacitor C in parallel with the injected capacitance from the modulator, designated as Cm. Since the two capacitors are in parallel, to get the total effective capacitance their individual capacitances are added. Therefore for the case under consideration the total effective capacitance, call it C,, is equal to Cm + C. Hence, the new resonant frequency of the complete tank circuit with its added capacitance is equal to:
fr= 1 / 2 pi __/ V L(C + Cm)
or fr=1/ 2 pi __/ L Ct
where Ct = C + Cm
If the injected reactance is inductive instead of capacitive, the new frequency determining tank circuit is as shown in Fig. 3-10. Instead of two capacitors in parallel there are two inductors in parallel. One inductor, that of the oscillator circuit, is designated as L, and the other inductive component, from the reactance tube modulator, is designated as Lm. The new frequency of oscillations is determined by the total effective inductance and the capacitance in the circuit. The total inductance, call it Lt, is equal to the two inductances L and Lm in parallel. Inductors in parallel are not added the way capacitors in parallel are added. Inductors in parallel resemble resistors in parallel.
To get the total inductance of two inductors in parallel we take the reciprocal of each, thus:
__!_ = __!_ + _!_ Lt L Lm 1 _L+Lm Lt -LXLm h L LXLm
were t= L+Lm
Consequently, the resonant frequency of the new tank circuit is.
t .. 1 r 21T~
Or to put it in terms of all the inductances: As a typical example we can assume that the injected reactance from the modulator tube is capacitive and equal to 50 µµf.
Also the inductance L of the tank circuit is equal to 100 microhenrys (100 X 10^-6 henrys) 2 and the capacitance C equal to 50 µµf (50 X 10^-12 farads).
[2. For a complete understanding of what is meant by the numbers 10^-6 or 10^-12 or similar ones see the section on "Powers of Ten," in the appendix. ]
Under these circumstances the frequency of oscillations is determined as follows:
1 21T -{Ls where Ct= C + C,,. = 50 + 50 = 100 µµf for 100 X 10^-12 farads.
Therefore, fr -
1 21T l 100 X 10 6 X 100 X 10-12 1 2 X3.14 -V 10,000 X 10-tB l 6.28 x 100 x 10-0
1.59 megacycles
Consequently, under the foregoing stipulated conditions the frequency of oscillations of the circuit, without an audio signal applied to the control grid of the reactance tube modulator, is equal to 1.59 mhz or 1590 khz. This is called the resting or center frequency of the oscillator. If there is an audio signal applied to the grid of the reactance tube, the bias on this grid will change in accordance with this audio signal. Hence, the transconductance or gm of the tube will also change, and thus the output reactance across the LC tank circuit will vary. If this change in gm is such that the fixed injected capacitance of 50 µµf is varied to a maximum of 55 µµf from a minimum of 45 µµf, the resonant frequency will change accordingly. The change in the resonant frequency will be approximately 40 khz on either side of the resting frequency of the oscillator-modulator circuit. The variation of this injected reactance is not instantaneous from the value of 50 µµf to 55 µµf or to 45 µµf but these are the maximum and minimum values of injected capacitances respectively, and, when the afore-mentioned audio signal is being received by the reactance tube, the value of injected capacitance varies from instant to instant. This indicates that the frequency of oscillations of the complete circuit is also different at every instant and changes directly with the audio signal. Thus, it is said that a reactance tube used in the fashion just described, frequency modulates the resting or center frequency of the complete circuit.
In brief, the effect of such a system of FM is that the reactance tube offers a reactive output varying with audio input so that this varying reactance changes the frequency of some oscillator circuit. Thus, a practical system, wherein the frequency of a carrier signal is varied directly, causing an FM signal, is obtainable. At this point it should be stressed that the oscillator circuit used for direct FM systems should not be fixed in value, as a crystal oscillator, but its frequency should be capable of varying over the desired range. In a crystal oscillator, injecting a reactance across the crystal circuit will vary the frequency by a minute amount, not enough to cause the FM that is desired. What does happen is that the reactance tube causes p.m. when used with a crystal oscillator. This will be seen later when the different p-m systems are discussed.
In comparing AM with a practical system of FM (as that just discussed) a few important points of difference between the systems should be stressed. First of all, in the a-m form of transmission the audio modulating signal causes the amplitude of the carrier to vary in accordance with the amplitude of the audio, whereas in FM the audio signal causes the frequency of the carrier signal to vary in accordance with the amplitude of the audio. Secondly, the AM of the carrier signal is accomplished after the frequency multiplication stages (if any), whereas in FM the modulation is accomplished before the frequency multiplication stages. In fact, in direct FM the modulation is accomplished within the first stages of the transmitter. In this respect, AM also differs from FM in that the former is achieved by modulating the final carrier frequency (that frequency termed the transmitting frequency) whereas the latter is achieved by modulating the resting frequency of the oscillator before multiplication. The FM occurs before the frequency multiplication in order to multiply the frequency deviation or frequency swing from the original resting frequency of the oscillator. This will be discussed in greater detail in a later section of this Section on frequency multiplication.
A third and important difference between these two types of modulation is, as mentioned previously, the amount of power involved in modulation. In AM the total power involved is split between the final carrier and the two sidebands involved, with 50 percent of the power in the carrier component of the final a-m wave and 50 percent in the sidebands, for 100 percent modulation. Therefore, for efficient transmission of intelligence the percentage of modulation should be as high as possible (up to 100 percent) and hence, a great deal of audio modulating power is needed. In FM comparatively little power is in the center frequency component of the FM wave, which is often smaller than some of the sidebands involved. Most of the power is vested in the many sideband components. Under these circumstances the power required for modulating in FM is very small compared with that used for AM In FM the total radiated power is constant, regardless of modulation. In AM the r-f power of the modulated wave is greater than that of the unmodulated wave. Therefore, in FM the power requirements of the transmitter are not affected by modulation; but in AM more power is required when the carrier is modulated than when it is not. Consequently, receiving type tubes can be used for the modulator section of FM transmitters instead of the power tubes used in AM.
Up to this point, we have dealt with a form of direct FM by employing reactance tubes. Although this type of direct FM was stressed, it is by no means the only type of direct frequency modulator. There are many other types of direct FM systems which also have practical possibilities, and some are used in the transmitters in operation today.
Reactance tube frequency modulators were shown because they are the most universally discussed type and, it is believed, the most important. Any type of a circuit that offers a variable reactive output with input audio voltage can be used as a direct FM system.
Phase Modulator
In the foregoing analysis of direct FM it was stated that the oscillator employed could not be a crystal oscillator because crystal oscillators are considered to be approximately fixed in frequency. In other words, the oscillator employed should be able to shift in frequency over a relatively considerable range. Such oscillators are often called variable frequency oscillators (abbreviated V.F.O.) Even though V.F.O.s are used in direct FM systems, they have a tendency to drift away from their center frequency, and control circuits are often employed to stabilize the oscillator center frequency. The control system employed to check this drift in frequency is termed an automatic frequency control system ( abbreviated afc), and it will be analyzed later in this Section. In indirect FM or p-m systems crystal oscillators are employed instead of V.F.O.s., because a fixed frequency is desired and the phase of this fixed center frequency is the characteristic to be modulated.
Despite the fact that the terminology of FM originated with Armstrong's system, his design is really not one of direct FM but rather one of p.m. This system will be analyzed in the next section. However, since p.m. causes an equivalent FM and, in effect, an FM signal is transmitted from Armstrong's transmitter, the terminology of FM stems from his design.
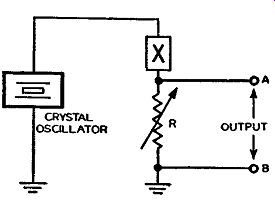
Fig. 3-11. The series combination of reactance X and resistance R, in
parallel with the crystal oscillator, is the time-delay network that
provides a phase change to the crystal oscillator frequency.
As has been shown, when a carrier is frequency modulated, its instantaneous frequency is deviated away from the center or resting frequency by an amount determined by the amplitude of the audio signal. In p.m. a similar situation exists. When the carrier signal is phase modulated, the instantaneous phase of the carrier deviates away from its resting position before modulation. It is evident that such a p-m signal can be had if the carrier is passed through some time-delay network which will make the carrier change in phase. Furthermore, if this time-delay network is made to vary in accordance with the amplitude of some audio signal, this network will change the phase of the carrier in conformity with this audio signal, and the resultant output from the time-delay network will be a p-m signal. It should be remembered that the center frequency is determined by some sort of a crystal oscillator circuit, so that it is stabilized and has very little chance to shift in frequency. Thus in p.m. it can be said that the instantaneous phase of the carrier signal is varied, while the amplitude and frequency remain constant. This instantaneous change in phase shift produces an equivalent or indirect change in frequency of the signal. This was shown in Section 1. There are many methods of producing p-m signals. Many of them are practical and many are not.
It is not the purpose of this section to illustrate all the different types of phase modulators in existence. However, a basic phase modulator circuit will illustrate how p.m. can be produced.
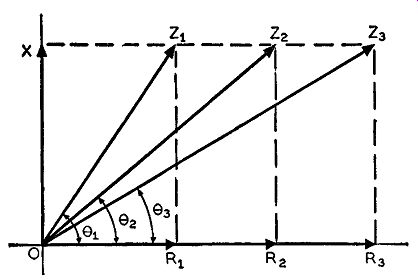
Fig. 3-12. Vector diagram showing the functioning of the circuit of
Fig. 3-11. The phase angle theta varies inversely with change in resistance
R and directly as the impedance Z.
Fig. 3-11 shows a simple p-m circuit which consists essentially of a crystal oscillator in parallel with a series combination of a reactance X and a resistance R. This series combination of X and R is the time delay network that imparts a phase change to the crystal oscillator frequency. The output voltage of this circuit is taken across terminals A and B. The system works as follows: Without the time-delay network, the frequency of the oscillator has a certain phase relation of its own. With the time-delay network wired across the oscillator circuit, as shown, the resistive and reactive components together are so chosen (at fixed values) that they offer a phase change in the oscillator frequency at some specific value between 0 and 90 degrees, the exact amount determined by the fixed values of X and R. Making the resistance R variable, likewise makes the phase of the oscillator frequency variable, and the oscillator output voltage across terminals A and B then varies in phase.
The way the XR network causes a phase shift is easily explained by the vector diagram of Fig. 3-12, in which X represents the fixed value of reactance and the R's represent different values of the variable resistance R. As there is a 90-degree phase difference between a pure reactance and a pure resistance, the reactive and resistive components are drawn vectorially at right angles to each other. If the initial value of resistance is equal to R2 then the total impedance of the series reactance-resistance network will be found by simple vector addition (see appendix). Therefore, the impedance for this first case, where the resistance is equal to R2, is equal to resultant vector Zs which is the result of the vector addition of X and R2. The angle 0s that Z9 makes with the horizontal line is the phase angle of the system. When the oscillator current flows through the series circuit of X and R (of Fig. 3-11) with R equal to R2, the impedance Z2 of the system brings about an instantaneous phase angle change between the oscillator cur rent and output voltage, equal to theta_2. If the value of resistance is increased from R2 to R8, the total impedance also will increase. and by vector addition this impedance is equal to the resultant vector Z8 in Fig. 3-12. Once the resistance has increased, the phase angle will change, and from Fig. 3-12 the phase angle under these circumstances is equal to 08 , which is less than that angle involved when the resistance is lower. If the resistance is de creased, from the starting value of Ra to R1 , the total impedance of the series XR circuit will likewise decrease. This decrease in impedance is represented by the impedance vector Z 1 in Fig. 3-12 which is the resultant vector of the vector addition of X and R1. Under these circumstances the phase angle again changes, but this time it increases to a value equal to theta_1. It is thus seen that the phase angle of the impedance network of Fig. 3-11, changes with change in resistance and, consequently, the crystal oscillator output is varied in phase and is said to be phase modulated. Further study of the vector diagram will reveal that the larger the value of R the greater will be the value of impedance, but the phase angle will approach zero degree, which means that the reactance X under this condition has negligible effect on the impedance and phase angle. If, conversely, the resistance gradually decreases to a smaller and smaller value, the impedance will also decrease accordingly, and the phase angle of the impedance will approach 90° but will never be greater. Under this circumstance the resistance will have negligible effect, and the impedance will be almost a pure reactance.
From this analysis it is seen that the phase changes in the circuit of Fig. 3-11 will always lie between 0 and 90 degrees. This is tantamount to saying that the impedance vector (that resultant vector caused by the vector addition of X and R) of Fig. 3-12 can rotate anywhere be tween the horizontal resistance reference line and the vertical reactance line of X. Since these two lines are at right angles to each other, that is, 90° apart, the impedance vector can have ph2.se angles only between O and 90 degrees, the exact value being determined by the instantaneous setting of the variable resistance R of Fig. 3-11.
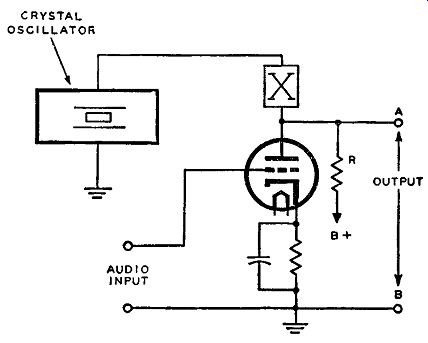
Fig. 3-13. A simple p-m circuit in which the variable resistance of
Fig. 3-11 is replaced with a triode and a-f input signal. The effective
resistance is the dynamic plate resistance of the tube in parallel with
the load R.
A simple circuit like that of Fig. 3-11 not only can produce a p-m output, but also can be advanced to the point where the resistance R is made to vary in accordance with an input audio voltage. The circuit for such a system is illustrated in Fig. 3-13. The only difference be- tween the circuits of Figs. 3-11 and 3-13 is that the variable resistor in the former circuit is replaced by the triode tube in the latter. It must then follow, in order for the two systems to function in the same manner, that the triode tube and its associated network act as a variable resistance. This is exactly what occurs. The dynamic plate resistance of the tube in parallel with the load resistor R is the effective resistance between the low side of the reactance X and ground.
This plate resistance is made to vary in accordance with the audio input signal across its grid, and the plate resistance variation causes p.m. of the crystal oscillator frequency. It is more fully explained as follows.
Without any audio signal input to the triode, a definite amount of plate resistance exists which is determined by the fixed cathode bias and the plate voltage. (R can easily be made considerably larger than the plate resistance, in which case its effect is negligible.) As it now exists this system offers a fixed phase relation to the oscillator frequency. However, if an audio input signal is impressed across the grid, so that the tube is still operative on the linear portion of its ib-ec curve, the plate resistance will vary in accordance with the grid voltage, and this variation of resistance is, therefore, linear. That is, the plate current ib will change accordingly as the instantaneous grid voltage is changed. In effect, then, the varying grid voltage, due to an audio signal, changes the existing value of the plate resistance of the triode, which then changes the instantaneous phase of the oscillator frequency in accordance with the audio signal. Thus, it is said that the oscillator frequency is phase modulated in accordance with the audio input signal. In the case just illustrated, the time-delay network is the reactance X in series with the dynamic plate resistance of the triode amplifier.
This network is one of the simplest types of phase modulators. There are other basic types, as previously mentioned, but they are too numerous to illustrate here. They are all generally the same in that they cause an instantaneous change in the phase of the oscillator output. In conclusion, then, we can say that in a p-m signal the frequency and amplitude of the carrier remain fixed, but there is an instantaneous change in the phase of the signal.
In direct FM the carrier or resting frequency of the oscillator is deviated on either side of its center position, the amount of deviation being determined by the amplitude of the audio signal. In p.m., the frequency of the oscillator has its phase deviated on either side of resting phase of the oscillator frequency. Concisely stated, frequency deviation exists in FM and phase deviation exists in p.m.
It might be well to mention that reactance tubes (not necessarily in quadrature operation) in conjunction with a crystal oscillator will cause p.m. Since the stability of the crystal frequency prevents the oscillator from being frequency modulated (that is, having frequency variations take place), the final result is that the phase of crystal frequency is changed in conformity to the changing reactance.
Automatic Frequency Control
As previously stated a form of reactance tube is used in a system called automatic frequency control (afc) to stabilize the center frequency of the oscillator in FM and a-m transmitters. This system is very important in that it uses a discriminator tube similar to those used in many FM receivers. Afc circuits have also been used to some extent in a-m receivers where it was desired to stabilize the frequency of the receiver oscillator.
In the reactance tube modulator the audio input controlled the amount of reactance the tube injected into the oscillator circuit, thus causing a deviation in the center frequency of the oscillator. How then in an afc circuit employing a reactance tube, can an injected reactance be made to stabilize the oscillator frequency, when at other times it is used as a modulator to shift the frequency? This question warrants some careful consideration. To realize fully how afc works, it will be best to examine a circuit employing afc. Such a circuit is shown in Fig. 3-14, and it can be representative of either a transmitter or a receiver circuit. The output of the oscillator is connected to some kind of heterodyning system. In a superheterodyne receiver, the heterodyning system is the already existing converter arrangement. In a transmitter, a separate heterodyning system is employed in order to obtain the necessary i.f. used for the production of an afc voltage. The primary and secondary tuned circuits of transformer T1 are resonant at the true i.f. of the system. Therefore, when the set is operating properly and the oscillator is stable, the operating i.f. will be at the center of the curve of discriminator transformer T1. In this case, the operation of the discriminator is such that at point A there is zero voltage, and the only voltage on the grid of the control tube is the audio, which contains no d-c component. This means that with the oscillator stable the average injected reactance is of a constant value, and naturally the oscillator does not change its average ( or center, or rest) frequency. That is, the so-called stable operating frequency of the oscillator takes into account the fixed average injected reactance of the control tube.
What happens when the oscillator shifts in frequency due to some instability? When the oscillator shifts in frequency it means that, in the process of heterodyning, the i.f. that is produced is not at the same frequency as that to which transformer T1 is tuned. The result is that there are unequal voltages distributed across the two halves of the secondary of transformer T1, which results in a change in the output of the discriminator at point A. This output voltage called the control voltage is fed directly to the control grid of the reactance tube, and this changes the effective bias on the grid from the steady voltage that had previously existed there. As a result the average plate current of the tube changes, in turn changing the average gm of the tube. Since the gm changes the reactance injected into the oscillator tank circuit, the average frequency also changes. The change in the injected reactance changes the average frequency of oscillations such that the oscillator returns to its original operating frequency and the oscillator becomes stable again.
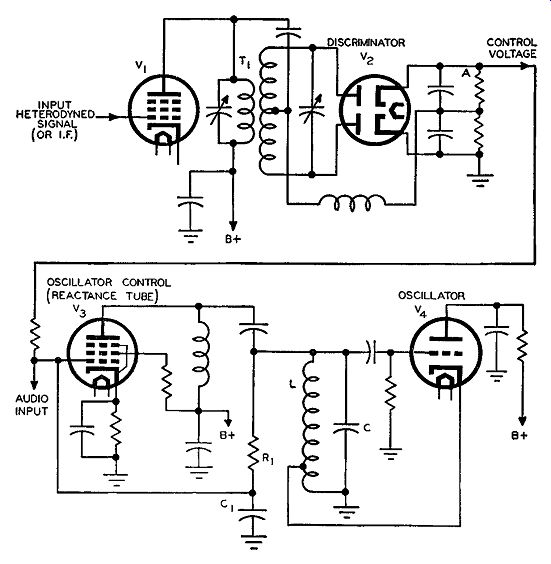
Fig. 3-14. An automatic-frequency-control circuit, which can be representative
of being used in either a transmitter or receiver.
In the circuit shown in Fig. 3-14 the injected reactance is inductive and is inversely proportional to the transconductance of the reactance tube. (See part (B) of Fig. 3-7.) The heterodyning system used with Fig. 3-14 is assumed to be working with the frequency of the oscillator (tube V 4 in Fig. 3-14) above the other signal used for the process of heterodyning. If the oscillator suddenly becomes unstable and decreases in frequency, the operating i.f. also decreases in frequency.
The discriminator circuit then functions so that at point A, a positive voltage appears. The magnitude of the voltage depends upon the number of cycles the oscillator is off tune. Therefore, the effective bias (due to the cathode voltage) on the control tube is decreased. This decrease in bias increases the Om of the control tube. With the g,,. increased, the injected inductance is decreased. This is true because the injected inductance for the circuit of Fig. 3-14 is equal to R1C1/g,,.[See Fig. 3-7 part (B) ].
Hence, the injected inductance that appears across the LC oscillator tank circuit is decreased from the value it had before the oscillator became unstable. If with two inductors in parallel we reduce the value of one of them, the total effective inductance also decreases.
This is what happens in the control tube-oscillator circuit. An injected inductance exists across the LC oscillator tank even when the oscillator is stable. The stable resonant frequency to which the set is tuned is determined by the capacitance C of Fig. 3-14 and the combined parallel inductance of Land the injected inductance. (This was indicated in the section on reactance tube modulators.) Consequently, if the injected inductance is decreased, the total effective inductance is also decreased, and, since the frequency of operation is inversely proportional to inductance (f = 1 /2 pi y LC), the frequency of oscillations increases. What has happened is that a detuning, or instability of some sort in the oscillator frequency, affects the reactance or control tube so that it injects a reactance across the oscillator tank circuit different from that already existing there. The amount of this injected reactance is determined by the amount of oscillator instability (that is, how many cycles off frequency), and the change in the total effective inductance is such that it stabilizes the oscillator frequency to the same frequency to which it was tuned before it drifted off frequency. In the case under discussion the value of the injected inductance was just enough to increase the frequency of the oscillator back to its stable position.
On the other hand, if the oscillator became detuned and increased in frequency, the afc system would function to decrease the frequency of the oscillator back to its original value. The way the system functions with an increase in oscillator frequency is as follows: The i.f. increases, which in turn causes a change in polarity of the control voltage at point A in Fig. 3-14. The polarity of this control voltage becomes negative with respect to ground, and a negative voltage is impressed on the control grid of the reactance tube. This in creases the bias on the tube, which in turn decreases the Ym of the tube. The decrease in gm causes the average injected inductance to increase, in turn increasing the total parallel inductance determining the average frequency of oscillations. When the total inductance in creases, the carrier frequency decreases, and the decrease is such that it returns the oscillator to its normal operating position. The accompanying Table 2 explains how the afc system of Fig. 3-14 works when the oscillator frequency becomes unstable and either increases or de creases away from its stable operating frequency.
-----------------------------
TABLE 2

Oscillator Frequency*
Intermediate frequency (i.f.) Polarity of control voltage
Bias on control tube Gm of the control tube
Injected inductance L1
= C1Rifgm
Total effective inductance
Lt = t ~ ~; 1
Frequency change f = --==-== 2 pi y CLt
Decreases Increases Decreases Increases Positive ( +) Negative (-) Decreases Increases
Increases Decreases
Decreases Increases Decreases Increases
Increases Decreases
------------
Under the assumption that the oscillator is tuned above the frequency of the other signal. If the oscillator is tuned below this other signal, then one would interchange columns two and three below the first line.
---------------------
In FM transmitters that employ a system of afc, the circuit is often called a "center-frequency stabilizing" circuit. The signal frequency that is used to perform the heterodyning with the oscillator signal is usually crystal controlled to make sure that one of the frequencies of heterodyning is very stable. It might be suggested that the master oscillator in the transmitter be crystal controlled itself in order to stabilize the frequency. This cannot be done in direct FM transmitters where the frequency of the oscillator must be "loose" and able to deviate away from its center frequency as caused by the action of audio modulating signal.
Frequency Multiplication
Up to this point we have dealt with reactance tubes and different types of modulator-oscillator circuits. We have also discussed automatic frequency control in which a reactance tube is used to stabilize the center frequency of the oscillator. Frequency deviation with respect to the audio and oscillator signals was also analyzed. What has not been investigated is the actual frequency of the master oscillator with respect to the final transmitted frequency. In this respect we have not analyzed exactly how the 75- khz maximum allowable peak deviation is obtained. Is it produced directly at the oscillator stage and if not, how does it get to such a high value? The final output signal from an FM or p-m transmitter is quite different from that produced at the oscillator-modulator stage. It might be thought that after the oscillator-modulator stage, the FM and p-m transmitters are exactly like the a-m transmitter, in that frequency multiplication stages and amplifying stages follow and that all systems function the same after this point. The truth of the matter is that frequency multiplication is not considered a necessity in AM, whereas it is considered a necessity in an FM or p-m system in order to obtain a good FM signal (especially in wide-band FM). In the FM and p-m transmitter block diagrams shown in parts (B) and (C) respectively, of Fig. 1-14 of Section 1, the stages following the oscillator-modulator stage are those of frequency multiplication.
Why is frequency multiplication needed in FM and p.m.? This question will be answered, along with many others on frequency multiplication, in the ensuing discussion.
Before examining the need for frequency multiplication, it will be wise to review a few features of frequency multiplication in general.
As was pointed out previously, frequency multipliers are used in a-m transmitters for the primary purpose of increasing the frequency of the local transmitter oscillator. This is also one of the reasons why they are used in FM, but there is another equally important reason, as will be seen later.
Some details of the way these so-called frequency multipliers in crease the frequency introduced into the grid should be explained.
Frequency multipliers are, in effect, harmonic generators. That is, a number of different frequencies exist within the frequency multiplier tube. These comprise the frequency input to the tube, which is considered as the fundamental frequency, plus numerous harmonics of this fundamental frequency. Consequently, if the output circuit of the frequency multiplier is so adjusted that it can choose any harmonic it desires, while being unselective to all other frequencies, this tube then acts as a harmonic generator. This is more clearly seen if we examine the circuit of Fig. 3-15.
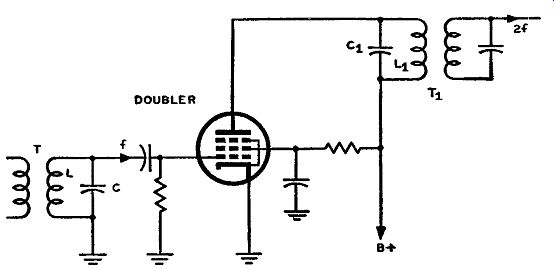
Fig. 3-15. A frequency-doubler circuit has its input transformer T tuned
to some frequency f and its output circuit T1 adjusted to 2f, the second
harmonic, the tube operating as a class C amplifier.
Transformer T is tuned to an input frequency f, which is impressed across the control grid. This frequency is called the fundamental frequency of the system. If the voltages on the tube are so adjusted that the tube functions as a class C amplifier, the plate current of the tube will be rich in harmonics of the input frequency. If, in the output stage of the tube, a tuned circuit T1 is placed, which is sharply tuned to the second harmonic, only this second harmonic will be selected by the L1C1 circuit. In other words the resonant frequency of L1C1 is twice that of the tuned circuit of LC. Consequently, the frequency that appears in the secondary of T1 is equal to 2f. When a tube functions so that its output circuit is tuned to the second harmonic, the tube is called a doubler. If the output circuit is tuned to the third harmonic the tube is called ;:i. tripler, and if it is tuned to the fourth harmonic, it is called a quadrupler. The doubler is the most common of the types of multipliers in existence, the tripler next, and the quadrupler last.
Even though frequency multiplication can go beyond the quadruple stage (that is, working in the fifth harmonic and higher), it is impractical to use any higher than this quadruple stage in transmitters.
It was stated that with the proper voltages on the tube, it would operate as a class C amplifier and the plate current would be rich in harmonics. Let us for a moment look into the analysis of class C operation as applied to harmonic generators. In Fig. 3-16 is illustrated a typical plate current-grid voltage characteristic curve of a class C amplifier (i_b-e_c curve.) A class C amplifier, by definition, is one which has its grid bias much greater than cutoff, so that plate current flows only when an alternating voltage is applied to the grid and this flow is for less than one-half cycle of the a-c grid voltage. This means that the plate current flows in short pulses.
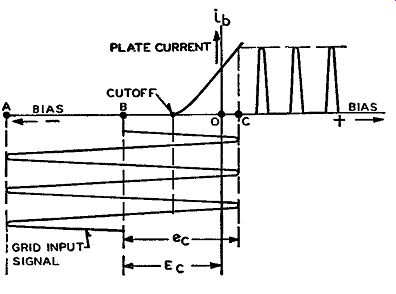
Fig. 3-16. A plate current-grid voltage characteristic curve of a tube
operating as a class C amplifier, which is one that has its grid bias
greater than cut off. Plate current flows in short pulses when an alternating
voltage is applied to the grid.
The bias (Ec) shown in Fig. 3-16 is equal to twice the cutoff. The alternating voltage applied to the grid has a peak value, designated as e_c, which is greater than the bias on the tube; hence, the grid is driven positive during a portion of this grid signal. Only during the portion of the alternating grid signal that is greater than the cutoff value of bias will plate current flow. Since appreciably less than half of this input grid signal is greater than the cutoff bias, the plate cur rent will flow only during this portion of grid signal. Consequently, the flow of plate current is also appreciably less than half a cycle, as is evident from Fig. 3-16. This flow of plate current is, therefore, in pulses, and the strength of these pulses depends upon the strength of the alternating grid voltage. The plate current, flowing as it does in pulses, is rich in harmonics, and once the tank circuit in the output of the tube is adjusted properly, it can be selective to any harmonic desired.
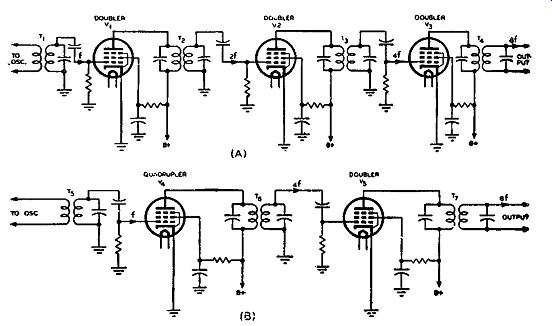
Fig. 3-17. Oscillator frequency can be multiplied eight times by either
or these circuits: (A) in which each of the three tubes is a frequency
doubler and (B) wherein the first tube multiplies the frequency four
times (quadrupler) and the other tube is a doubler.
There are other types of harmonic generators, but in the frequency multiplication stages of FM transmitters the type of multiplication generally employed is that utilizing class C amplifiers.
More than one frequency multiplication stage can be used. The amount of multiplication and the number of stages required is determined by the transmitter oscillator frequency and output frequency of the transmitter. For instance, the oscillator in a transmitter may operate at a fundamental frequency f, equal to 100 khz, and it is de sired that the transmitter have a frequency of transmission equal to 800 khz. To obtain the correct output frequency two different combi nations of multiplication are possible and these are illustrated in Fig. 3-17.
In part (A) three multiplication stages are used. Each stage employed functions as a doubler and has its output tank circuit tuned to the second harmonic of the input signal to the grid of the same tube.
Transformer T1 is tuned to the fundamental frequency f ( 100 khz) of the oscillator. The first doubler tube V1 being operated class Chas its plate current flow in pulses and, therefore, is rich in harmonics.
Transformer T2, in the output circuit of tube V1 and across the input circuit to tube V 8, is tuned to the second harmonic of the oscillator frequency, and consequently it is highly selective to this second harmonic. By transformer action this new frequency, now equal to 2f or 200 khz (the second harmonic off) is impressed across the grid of tube V1. This tube is also operated class C, and its plate current is rich in harmonics. Transformer T 8 is tuned to the second harmonic of the input signal of tube V2, namely the signal equal to 2f, or 200 khz, and the tube functions as a doubler in that the output frequency is twice that of input. The input frequency is equal to 2f or 200 khz, and the output frequency from T3 is equal to 4f or 400 khz. Which is to say that transformer T3 is tuned to the fourth harmonic of the oscillator.
Output signal 4f or 400 khz is transformer coupled to the next tube, V 8, which also acts as a doubler. This means that transformer T 4 is tuned to twice the input signal to tube V3. Since the input signal to this last tube is equal to 4f or 400 khz, the output signal from this stage is equal to 8f or 800 khz, which is the required transmitting frequency.
This is equivalent to saying that transformer T4 is tuned to the eighth harmonic of the oscillator.
This result can also be obtained with the two-stage frequency multiplication system of part (B) of Fig, 3-17. In this system the first tube acts as a quadrupler and the second tube as a doubler. Both tubes function under class C operation, and hence the plate currents of both are rich in harmonics. The input signal to the first stage, tube V4, is from the oscillator and equal to 100 khz or f. The tuned transformer, T 6, in the output of this stage is resonant at the fourth harmonic of this input signal, and consequently a signal of frequency equal to 4f or 400 khz is impressed across the grid of tube V5 by transformer action of T 6. The transformer T 7 in the output circuit of tube V 5 is tuned to the second harmonic of the input signal to tube V5, so that the final output signal is equal to 8f or 800 khz which is the same result as that obtained in the former case.
Thus, it is readily seen how frequency multiplication can take place.
The frequency involved in the foregoing problems is an unmodulated carrier. This is typical of a-m transmitters where the modulation takes place after frequency multiplication. In FM and p-m transmitters the modulation takes place before the frequency multiplication stage. There is a definite reason for having the frequency multiplication stages so arranged. The reason for this will become evident in the next section.
The Need for Frequency Multiplication
Amplitude modulation is primarily concerned with two types of frequencies -- namely, the carrier frequency which exists at any one instant and the modulating audio frequency. In FM we are concerned with another frequency besides the two associated in a-m systems.
This other frequency is known as the deviation frequency. (In p-m systems instead of the deviation frequency we are concerned with a phase deviation.) In FM transmitters the importance of frequency multiplication is twofold. One use is to increase the instantaneous value of the oscillator frequency, and the other to increase the amount of frequency deviation. (In a p-m system, it is the phase deviation or its equivalent frequency deviation which must be increased besides the oscillator frequency.) In direct and indirect FM the final trans mitted frequency is quite high. In the old FM band it was anywhere from 42 to 50 mhz, whereas in the new band it is more than twice as high, being anywhere between 88 and 108 mhz. If a variable frequency oscillator (vfo) were to produce such high frequencies, the oscillator would be extremely unstable at these high frequencies. The slightest amount of instability may throw the oscillator off by a very small percentage and around 100 mhz this percentage of instability is quite a number of kilocycles. Consequently, the oscillator works at a much lower frequency, and by the use of frequency multiplication the necessary frequency of transmission is reached.
Some might make the suggestion that automatic frequency control, afc, be employed at these high oscillator frequencies to prevent oscillator drift. The idea, although well founded, is not applicable to oscillators at these high frequencies. While an afc circuit may stabilize oscillator drift, the afc circuit itself is not 100 percent perfect, and, when operated at 100 mhz, it does not provide sufficient stability.
Crystal controlled oscillators are not used at these high frequencies (even though crystal oscillators are very stable) because it is a practical impossibility to manufacture crystals to operate at such high frequencies. Therefore, even with crystal controlled oscillators employed in transmitters (especially p-m transmitters), frequency multiplication has to be used to increase the fundamental frequency of the oscillator to the desired frequency of transmission.
If frequency multiplication were employed only to increase the oscillator frequency, as in AM, the problems would easily be solved.
However, we have to take into account the deviation of the oscillator signal in frequency when FM is used and in phase when p.m. is used.
When modulation occurs in either direct or indirect FM, the deviation of the center .frequency of the oscillator is not so great as is necessary for the final output signal from the transmitter. In other words, the desired frequency deviation (or phase deviation) as required for proper FM broadcasting cannot be obtained directly from the modulator. Hence, to overcome this difficulty, frequency multiplication is used to increase the amount of deviation.
The final result is that frequency multiplication, as employed in FM transmitters, serves two purposes. It increases the center frequency of the oscillator to the desired value for transmission, and, at the same time, it increases the amount of deviation (frequency or phase swing) of the center frequency of the oscillator to that necessary for correct transmission.
Increase of the deviation is the important problem in frequency multiplication of FM It is the deviation that determines the effective bandwidth of the transmitter. Most commercial transmitters today operate on the basis of 75- khz peak deviation for 100 percent modulation, as standardized by the FCC. This means that the peak-to-peak deviation is 150 khz. This type of FM is known as wide-band FM When there is reference to narrow-band FM it means that the frequency deviation used is much smaller than that employed in wide-band FM.
More will be said about narrow-band FM in the next Section.
Understanding how the deviation frequency is multiplied along with the instantaneous oscillator frequency entails some knowledge of the character of the deviation frequency. We know that the amplitude of the audio modulating signal determines how .far the center frequency of the oscillator will shift in frequency, which shift is commonly known as the frequency deviation of the center frequency. At any one instant of time, within the range of frequency deviation, there exists a value of frequency called the instantaneous frequency.
The difference between this instantaneous frequency, call it f1, and the center or resting frequency, call it fc, of the oscillator is called the deviation frequency fa,. At any one instant of time, fa, can have only one value. In frequency multiplication it is the instantaneous frequency, f 1, which is multiplied because it is an inherent part of the FM wave. This means that both fc and fr are effectively multiplied by the same amount; and therefore, the deviation frequency, at any one instant of time, is multiplied by the same amount. For example, sup posing that the center frequency, f c, of an FM signal is equal to 100 khz and that, at a certain instant of time, the instantaneous frequency, fr, is equal to 105 khz, then the deviation frequency, fa,, would be: fa,= fr - f c = 105 - 100 = 5 khz If this FM signal is impressed across the grid of a tube that is operating as a doubler, then, in the output circuit of this tube, the center frequency of the carrier will be doubled, and the new frequency equal to 2f0. Similarly, the new instantaneous frequency is equal to 2f r. The deviation frequency at the output of this doubler stage is the difference between the center frequency and the instantaneous frequency that exists at the output of this stage at the particular instant of time under discussion. Under these circumstances the deviation frequency at the output of the doubler stage is equal to = or or 2f1-2fc 2 X 105-2 X 100 210-200 = 10 khz.
From this analysis it is obvious that the amount of deviation frequency is multiplied by the same amount as the resting frequency of the oscillator and the instantaneous frequency, no matter what type of multiplier is used. It is, therefore, seen that modulation in FM transmitters takes place before frequency multiplication because the deviation frequency, also, has to be increased.
If the center frequency of an oscillator is equal to 12.5 mhz and the desired frequency of transmission for FM is 100 mhz, a total multiplication of 100/12.5 or 8 times the oscillator frequency is needed. If the peak frequency deviation of the 12.5-mhz center frequency is equal to 7.5 khz, the peak-to-peak swing of the deviation frequency is equal to 15 khz. Upon the proper multiplication, the final output peak-to peak deviation will be 15 X 8 = 120 khz. This means that, for the system above, the final output center frequency is equal to 100 mhz after multiplication, and the peak-to-peak .frequency deviation of the 100-mhz signal is equal to 120 khz.
The multiplication system that performs this increase in carrier frequency and deviation can be either three doublers or a quadrupler and a doubler. After the initial stage of frequency modulation in the former case, the FM signal is at a center frequency value of 12.5 mhz with a peak frequency deviation of 7.5 khz. The true frequency extremes of the signal are 12.5 mhz plus 7.5 khz and 12.5 mhz - 7.5 khz or in more concise mathematical terms 12.5075 and 12.4925 mhz. If the latter type of multiplication is employed, then after the quadrupler stage the frequency extremes would be 4 X 12.5075 and 4 X 12.4925 mhz or 50.03 and 49.97 mhz. Therefore, at the input to the doubler stage the peak-to-peak frequency deviation is equal to 50.03 mhz - 49.97 mhz = 0.060 mhz or 60 khz. After the doubler stage, the final output frequency extremes would be 2 X 50.03 and 2 X 49.97 or 100.06 and 99.94 mhz. The final peak-to-peak deviation frequency would then be equal to 100.06 mhz - 99.94 mhz = 0.120 mhz or 120 khz which is the required amount, as indicated in the preceding paragraph. This means that the final FM wave of a carrier frequency of 100 mhz is swinging 60 khz on either side due to the amplitude of the audio modulating frequency and amount of multiplication employed.
A similar numerical analysis relative to indirect FM or p.m. can be shown to exist. However, it suffices to say that frequency multipliers also multiply the amount of phase shift or phase deviation that occurs in these types of transmitters.
Amplitude to Phase to Frequency Modulation
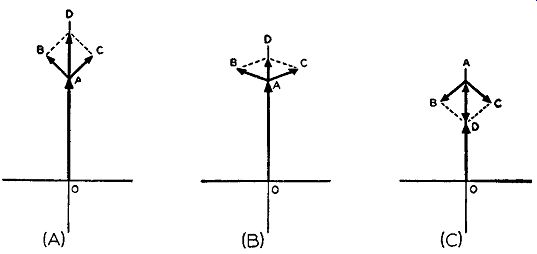
Fig. 3-18. In an a-m signal, the addition of the two sidebands is such
that the double sideband (vector AD) when added to the carrier (vector
OA) will produce a resultant signal (vector OD) constant in phase in
all cases.
At this point we are prepared to study some of the oscillator-modulator stages besides the simple ones already studied, that are found in FM transmitters. In this respect the Armstrong system of modulation will be analyzed first. However, before analyzing the Armstrong system, a few facts not previously discussed about AM and FM should be brought to light. These concern the relation between the sidebands and the center frequency component of both modulated waves under the conditions of a slight amount of modulation.
In Section 2 it was pointed out that, when the modulation index or deviation ratio is small, the number of effective sideband pairs is likewise small. Referring back to Table 1 in Section 2, it is noted that when the modulation index is less than ½ there is only one effective sideband pair, that is, one sideband on either side of the center frequency component. Thus the components of the FM wave when the modulation index is below ½ are similar to those of AM in which only one pair of sidebands appears, no matter what the percentage of modulation. If the degree of modulation in FM is kept small enough, it is possible to have the frequency and amplitude of the sidebands and center frequency component of an FM signal equal to those components of an a-m wave. However, a difference does exist in the phase relation between the respective sidebands and the center frequency components. If the two sidebands of the FM wave are added together and if the two sidebands of the AM are also added together, in both instances a new wave will appear known as the double sideband signal. These double sideband waves represent the difference between the modulated waves and their respective center frequency components. Both double sideband waves would appear to be identical under the assumption that the individual sidebands for both types of modulation are equal in frequency and amplitude.
For the a-m case the addition of the two sidebands is such that the final combined sideband signal is in phase with the carrier frequency.
This is illustrated vectorially in Fig. 3-18. In parts (A), (B), and (C) of this figure, vector OA represents the peak amplitude of the un modulated carrier, vectors AB and AC represent the peak amplitudes of the two sidebands, AD represents the amplitude of the double side band, and OD is the final resultant a-m wave. The individual side bands (AB and AC) in an a-m wave rotate about; the tip of the OA vector. Consequently the resultant double sideband (AD) can be additive or subtractive from the carrier, in which case the final resultant wave will be of constant phase but will vary in amplitude according to the amplitude of the double sideband. For instance, in parts (A) and (B) of Fig. 3-18 the combined sideband is additive to the carrier, resulting in an increase in amplitude (with part (A) greater than part (B)), but the phase of the final wave remains the same. These two vector diagrams are representative of the a-m wave where the amplitude of the wave is greater than that of the carrier.
The vector diagram of part (C) of Fig. 3-18 is typical of that portion of the a-m wave where the amplitude is less than that of the carrier.
In this latter vector diagram, the amplitude of the vector representing the double sideband is subtracted from that of the carrier and a smaller amplitude results but the phase relationship of the resultant wave OD is still the same.
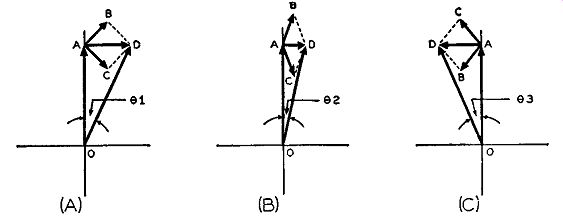
Fig. 3-19. In an FM signal, the double sideband (vector AD) is 90° out
of phase with the carrier (vector OA). The resultant vectors are never
smaller than that of the carrier.
In FM, even though the frequencies and amplitudes are equal for ,small deviation ratios, as previously specified, the situation is different from that of AM The double sideband is 90° out of phase with the carrier and this makes the situation considerably different from AM.
The vector representations are illustrated in Fig. 3-19. In these dia-grams the carrier, the sidebands, and the double sideband all are of the same length as those in Fig. 3-18. The double sideband vector AD of Fig. 3-19, in all cases, is 90° out of phase with the carrier vector OA. Consequently, the final resultant signal vector, OD is not always of the same phase with the carrier. In fact, the magnitude of the combined sideband vector AD is the determining factor in the change in phase of the resultant vector OD with respect to the carrier OA. This is readily noted in Fig. 3-19 where the phase angle for each part differs from the others. In part (A) of Fig. 3-19 the resultant vector OD is said to be lagging the carrier OA by an angle equal to theta_1. In part (B) the resultant vector OD is still lagging the carrier OA but by a smaller angle equal to 0s, In part (C), the resultant vector OD is leading the carrier OA by an angle equal to OB. The interesting thing in this case of FM is that the resultant vectors are never smaller in amplitude than the carrier.
It has just been demonstrated how the same carrier frequency and double sideband component can cause either AM or FM In either case, the modulation is slight, especially in FM where only one side band pair appears. This analysis provides a ready method of changing or converting AM to indirect FM A carrier signal is first amplitude modulated slightly and the sidebands are separated from the center frequency component. That is, the center frequency component is separated from the modulated signal, and all that remains is the double sideband. This double sideband then is passed through a time-delay network that shifts it in phase by 90°. If this phase-shifted double side band is combined with the original carrier wave, a frequency-modulated wave results. In terms of the vector diagrams, the double side band vector AD in parts (A), (B), and (C) of Fig. 3-18 is shifted in phase by 90° to yield the vector diagrams in parts (A), (B), and (C) of Fig. 3-19, respectively. This means that with an a-m wave phase shift is employed so that the final resultant wave will be equivalent to a p-m wave. This is the basic principle upon which the Armstrong transmitter operates.
The resultant vector OD in Fig. 3-19 varies in both amplitude and phase with respect to the carrier frequency. This variation in amplitude is undesirable in true phase modulation. It was stated previously that in p.m. only the phase is varied, while the amplitude of the modulated signal remains constant. In order to utilize properly the effect of a small amount of AM to obtain p.m., the amplitude variations in this final resultant p.m. have to be eliminated. This will be discussed in the next Section.
The Armstrong System
Since the most important contributions to the field of FM, as in most other fields, are the first accepted designs and accomplishments in the field, it follows that a discussion of them is in order. There is no need for elaboration about the man who is generally conceded to have made FM a commercial reality. The name of Armstrong is as well known in the field of FM as that of Lee DeForest in the field of radio tubes.
Of course, these men are not the only ones who had ideas that led to FM and the multielement vacuum tube in use today. On the contrary, the history of the pioneering in these fields antedates them. The most consideration is given, however, to the man who invents the first system that works and has commercial possibilities. In this respect Armstrong is the leader in the field of FM.
The Armstrong system received quite a lot of attention because it was the first transmitter allowed to operate by permission of the FCC. The Armstrong system is not direct FM but rather indirect FM, in which a shift in phase is used as the basis for obtaining the final FM wave. The method involved was basically outlined in the previous section. In this section we will analyze the basic Armstrong system in block diagram form, and in the next Section study some of the individual circuits comprising the system.
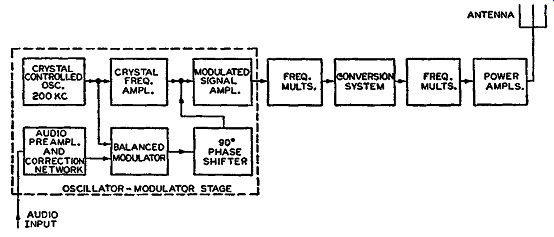
Fig. 3-20. Block diagram of the original Armstrong FM transmitter. The
complete oscillator-modulator stage is shown inside the dashed box. Note
that a frequency conversion system exists between the frequency multi
pliers stages.
Fig. 3-20 is a block diagram of the original Armstrong transmitter as operated on the old FM band. Although the transmitter in operation today is somewhat different (as will be seen in the next Section) the basic theory is essentially the same in both cases. That portion of the transmitter of Fig. 3-20 enclosed in the dashed box is the complete oscillator-modulator section. Its basic action is similar to that described in the preceding section. A carrier frequency of 200 khz is obtained from a crystal controlled oscillator. Such an oscillator offers good frequency stability compared with the variable frequency oscillators.
The output of this oscillator is fed into two different stages. Part of this carrier frequency signal is fed directly into an amplifier called the crystal frequency amplifier and part is applied to the input stages of a balanced modulator. If an audio signal of constant frequency is impressed across the audio input section, it will also, after passing through a preamplifier and correction network (the function of which will be explained later on), be applied to the balanced modulator net work. This balanced modulator is effectively in operation only when both the audio signal and the crystal carrier frequency are applied to it. The audio frequency then amplitude modulates the carrier frequency within the balanced modulator. The modulation is very slight (that is, percentage small) with the result that the sidebands are quite small in amplitude. The balanced modulator is so arranged that the center frequency component of this a-m signal is suppressed and only the double sideband component of the a-m wave appears in its output circuit. The upper and lower sideband components are combined (that is, added) to form the new signal designated as the double sideband.
This double sideband contains all the intelligence of the modulating signal. If, at one instant of time, the audio signal is equal to 1 khz, the two effective sidebands that are formed in conjunction with the 200- khz carrier signal are 200 + 1 khz and 200 - 1 khz, or 201 and 199 khz respectively. In terms of double sidebands, the double sideband relative to this numerical situation is the combination of a 201- khz signal and a 199- khz signal, under the conditions of equal amplitudes for each.
At the output of the balanced modulator, the double sideband has the relation to the carrier frequency shown in the vector diagrams of Fig. 3-18, where vectors AD represent the double sideband. This out put from the balanced modulator, being free of the center frequency component of the a-m wave, is applied to a phase-shifting network.
This latter network introduces a time delay to the double sideband output of the modulator that shifts the sideband in phase by 90 degrees. At the output of the phase-shifting network, the double side band signal has the relation to the carrier frequency illustrated by the vector diagrams in Fig. 3-19, wherein vectors AD represent the double sideband and vectors OA the carrier. The phase-shifted double sideband signal then is applied, together with the amplified crystal carrier frequency, to another amplifier. In this stage these two signals are combined to give essentially a p-m signal. This is indicated vectorially in Fig. 3-19. From this stage the new p-m signal is applied to a system of frequency multiplication and conversion in order to obtain the necessary deviation and carrier frequency output.
The foregoing analysis was based on the assumption that the audio modulating signal is constant in frequency. In this instance only the amplitude of the audio signal is a determining factor in the amount of phase deviation. However, if the frequency of the audio were varied, this would cause a change in the amount of frequency deviation proportional to the modulating frequency. This is an undesired characteristic because it was stated that in p.m. only the amplitude and not the frequency of the audio should vary the amount of phase deviation.
Since the audio frequencies involved in speech and music are by no means constant but vary over the complete audio range, there must be some means to prevent this variation of audio frequency from causing an increase or decrease in the amount of deviation. This is accomplished by the audio correction network, which is in the audio part of the system preceding the balanced modulator. This network effectively makes the p-m signal equivalent to an FM signal.
Each vector OD in the vector diagrams of Fig. 3-19 represents the resultant p-m signal. It is seen that these vectors vary in amplitude as well as phase. To insure negligible distortion, the phase angle changes are made very small. If the phase deviation exceeds a certain value, distortion will result. This puts a limit on the strength of the double sideband, because the carrier, when added to the double side band, controls the amount of amplitude and the phase of the resultant signal. To maintain linearity between modulating voltage and angular deviation, the amplitude of the double sideband is made very small compared with the carrier, so that the resultant p-m signal has an insignificant variation in amplitude. The amplitude limiting action of the following frequency multiplier stages will clean up most of this amplitude variation.
In the Armstrong system, as operated today, the initial amount of phase deviation is so adjusted that for 100 percent modulation (75- khz output peak deviation) the peak phase deviation for an audio frequency of 50 cycles is 11.06°, and this produces an output that is below one percent distortion. The curve of Fig. 3-21 will make this clearer.
This figure is a curve of initial peak phase deviation versus the percentage of output distortion. The system is so arranged that it operates at point A on the curve where, for an initial peak phase deviation of 11.06°, the distortion is approximately 0.9 percent. To find the exact amount of frequency swing that is equivalent to this phase swing of 11.06°, the lowest audio frequency that the set is designed to pass is multiplied by the amount of peak phase shift in radians. What has to be done is to change the 11.06° into radians. (One radian is equivalent to 57.3 °.) Therefore we have:
Peak frequency swing = 50 cycles X 15
0 Peak frequency swing= 50 X .193 = 9.65 cycles
Thus, for a minimum audio modulating frequency of 50 cycles (at less than one percent distortion), the 11.06° peak phase deviation is equal to a peak frequency deviation of 9.65 cycles. At first this small amount of frequency deviation makes it appear as though a tremendous amount of multiplication is needed to obtain the necessary 75- khz deviation for 100 percent modulation. This was true in the case of the original transmitter, but in the new Armstrong transmitter the actual amount of multiplication stages have been cut down. This will be seen in the next Section. In the original system for a peak frequency deviation output of 75 khz, the 9.65 cycles would have to be multiplied approximately 7500 times. However, this would indicate that the original crystal oscillator frequency of 200 khz, if passing through all these multipliers, would be multiplied out of the broadcast range of the FM bands. In other words the 200- khz crystal frequency multiplied 7500 times would result in an output carrier frequency of 1500 mhz, which is nowhere near the frequency band allotted to FM broad casting, either on the old band or the new band.
Fig. 3-21. Initial peak phase deviation plotted against percentage of
distortion in the output.
It has just been explained that the crystal oscillator frequency can not be multiplied as many times as the frequency deviation. If the same number of multipliers are used for the crystal oscillator frequency, how then is this effect of high carrier frequency output pre vented? This is accomplished by heterodyning down the carrier frequency after it has passed through a number of multiplication stages, as is seen from the block diagram of Fig. 3-20. The conversion system, appearing between a series of two multiplier stages, has two signals injected into it. One signal is obtained from a fixed crystal oscillator within the conversion block, and the other is the FM signal obtained after passing through a number of multiplication stages. These two signals beat together, and in the output circuit of the converter is a selective intermediate frequency network which selects only the difference frequency between the two. A new FM signal decreased in center frequency then appears at the input to the other multipliers, so that, when multiplied by the rest of the multipliers, the final carrier frequency output will be the exact frequency of transmission required. The whole crux of the situation is that the amount of frequency deviation is not changed by the system of conversion, thus enabling the correct carrier frequency and frequency deviation to be at the output of the transmitter.
To obtain the necessary FM output signal, the amount of p.m. that is procured is made inversely proportional to the frequency of the modulating audio signal. This is taken care of by the audio correction network, the analysis of which is given in the next Section.
Other Transmitter Stages
Up to this point we have dealt with those parts of the FM transmitters that are essentially different from those of the a-m transmitter.
The primary differences centered around the modulator, oscillator, and multiplication stages. These stages of FM are really the most important in the transmitter, because their purposes are so very different from those actually employed in a-m transmitters. The stages following the multiplication system in FM are very similar in circuit operation to those in AM These are the intermediate power amplifier and power amplifier stages.
One of the chief differences between the a-m and FM power amplifier stages is that in AM the modulation is accomplished somewhere within these power stages, whereas in FM the modulation is accomplished before the frequency multiplication stages. In either case, FM or AM, the primary concern of the power amplifier stages is to in crease the power of the signal to be transmitted. However, the tuned circuits in FM have to be designed to handle the high frequencies that are involved, and the tubes so chosen that they will be able to handle these frequencies. It should be remembered that the new FM band is around 100 mhz, about double the frequencies of the old FM band.
Another interesting feature is that in FM transmitters a consider able frequency deviation is involved. This means that the tuned circuits in the power stages or the set have to be broad enough to handle the maximum bandwidth that is associated with FM In wide-band FM, (that is, those FM transmitters employed for commercial broad casting in the 100 -mhz band) the maximum peak frequency deviation is equal to 75 khz for 100 percent modulation, which means that the tuned circuits in these transmitters have to be quite broad in order to avoid distortion. In narrow-band FM transmitters the bandwidth is not so large, so the tuned circuits in the power stages used are not too broad.
Aside from these two important considerations, the power amplifier stages in FM have to take into account the same factors as AM Since the operation of the new FM broadcast transmitters is in the 100 -mhz region, special neutralizing circuits have to be employed to counteract certain lead inductances and capacitances which have appreciable effect at these high frequencies.
An extremely important consideration for the correct operation of the FM transmitter is the design of the antenna system. If the antenna is not perfectly matched to the final power amplifier stage or if it is incorrectly situated, then no matter how well the remainder of the transmitter functions, the final transmitted FM signal will be of poor quality. Such factors as distortion, power loss, standing waves, and the like add to the poor quality of transmission when the antenna system is not properly designed. This topic of transmitting antennas will be discussed in greater detail in Section 5.
QUESTIONS
SECTION 3
3-1. With regard to the frequency multiplication stages of a-m and FM transmitters, where does the modulation take place in each before or after these stages? Give the reason for your answer for the FM transmitter.
3-2. In brief, what can be done to a simple R-L-C oscillatory tank circuit to amplitude-modulate it? To frequency-modulate it? Give the answers in terms of varying a circuit element.
3-3. What part does the frequency and amplitude of a modulating signal play in producing an FM wave?
3-4. What is the name of the basic type of tube circuit used to cause frequency modulation of a carrier signal?
3-5. a. What are the names and symbols of the three basic tube constants? b. Define gm and r1'. c. What is the mathematical relationship between g,,., r P' and µ.?
3- 6. a. In the basic reactance tube circuit, as seen in Fig. 3-4 on page 57, two impedances, Z1 and Zv are inserted in the output. If one impedance is reactive (capacitive or inductive), what must the other impedance be? b. According to the reactance tube circuit of Fig. 3-4, what are the four possible combinations of Z1 and Z2 that will permit the tube to function as a reactance tube?
3-7. The impedance that a reactance tube injects is not purely reactive but also contains a resistive component. What is done so that this resistive component has a negligible effect compared to the reactive component?
3-8. What is the phase relationship between the plate current and voltage across the output terminals of a reactance tube circuit in which the injected resistive component has a negligible effect? Discuss the phase relationship with regard to the injected reactance being capacitive in one case and inductive in another.
3-9. a. Upon what characteristic of a vacuum tube does the injected impedance (both the resistive and reactive components) of a reactance tube depend?
b. Does the injected resistance which is in series with the injected reactance of a reactance tube, depend upon the resistor in the out put circuit of the tube, whether this resistor is represented by Z1 or Z2 in the output circuit of Fig. 3-4? Explain.
c. If the gm of a reactance tube is equal to 5000 micromhos, what is the injected series resistance?
d. When it is desired to keep the injected series resistance of a reactance tube as low as possible, is it best to use a tube having a high or a low transconductance? Why?
3-10. a. Assume a reactance tube circuit as shown in Fig. 3-7 (B) on page 60, where R is equal to 50,000 ohms, C is equal to 50 µµf, and the Ym of the tube used is equal to 7500 micromhos. What is the value of injected inductance?
b. If an audio signal input to the grid of this tube is such that gm of the tube varies 2500 micromhos above and below the 7500-micro mho value, what is the total variation in injected inductance?
3-11. Assume a reactance tube modulator circuit as shown in Fig. 3-8.
3-12.
3-13.
a. What components determine the frequency of oscillations of the circuit with no audio input to the grid of the reactance tube?
b. If Z 1 is a capacitor and Z2 a resistor, will the frequency of oscillations decrease or increase when the gm of the reactance tube in creases?
c. If Z1 is a resistor and Z2 a capacitor, will the frequency of oscillations decrease or increase when the gm of the reactance tube de creases? Assume a reactance tube modulator circuit similar to that of Fig. 3-8, with no audio applied and a fixed value of 300 microhenrys inductance injected across the L-C oscillator circuit.
With this injected inductance and elements L and C, where L is equal to 500 microhenrys, the oscillatory frequency equals 5 mhz.
If upon application of an audio signal the g_m of the reactance tube changes in such a manner that the injected inductance varies 25 microhenrys above and below its original injected 300-microhenry value, what is the peak-to-peak frequency deviation of the FM signal produced? What is the maximum and minimum instantaneous frequency of the FM signal? Are crystal oscillators used as the master oscillator to produce an FM signal in direct FM transmitters? Why?
3-14. If a delay network, consisting of a reactance in series with a very high-valued (compared to the reactance) variable resistance, is shunted across the output of a crystal oscillator circuit, what is the maximum amount of phase change that can occur when the resistor is varied from its maximum to zero value?
3-15. In the circuit of Fig. 3-13, how can a linear variation in the dynamic plate resistance of the tube be secured?
3-16. In the automatic frequency control circuit of Fig. 3-14, what is the output voltage at point A when the oscillator frequency is stable?
3-17. For the circuit of Fig. 3-14, assuming the frequency of the oscillator tube V 4 to be higher than the other signal used for the process of heterodyning; then:
a. If the control voltage is such that the bias on the tube becomes less negative, has the frequency of the oscillator tube V 4 increased or decreased to cause this change?
b. If the oscillator tube V 4 shifts in frequency above its center or resting value, does the transconductance of the reactance tube in crease or decrease?
c. If the injected inductance from the reactance tube is said to de crease because of the instability of the oscillator tube V4, what must have happened to the resting frequency of the oscillator?
3-18. a. In FM transmitters, what type of amplifier circuit is used for frequency multiplication?
b. The output circuits of frequency multipliers are usually tuned to one of three harmonics. What are they?
c. Why is the output signal of a class C amplifier rich in harmonics?
3-19. a. What are the possible arrangements of the tubes in a frequency multiplication system utilizing any combination of doublers, triplers, and/or quad-ruplers to give an output frequency of 90 mhz for an input oscillator frequency of 7.5 mhz? The order of appearance of the multiplier stages is unimportant.
b. If a frequency multiplication system consists of a doubler, tripler, tripler, and doubler, in the order named, what is the output frequency of the first tripler stage for an input oscillator frequency of 7.5 me? The output frequency of this complete 4-stage multi plier system is considered to be what harmonic of the 7.5 -mhz oscillator frequency?
c. If the desired output frequency of a transmitter is 105.3 mhz, and a frequency multiplication system consisting of a doubler and two triplers is to be employed, what is the required oscillator frequency?
3-20. a. Why does the process of modulation in FM transmitters take place before frequency multiplication?
b. Given an FM transmitter with a multiplier system consisting of two doublers and one tripler, a master oscillator frequency of 8.0 mhz, and an initial peak frequency deviation of the oscillator signal equal to 4.5 khz, what is the center frequency of the final output FM signal from the transmitter and the final peak-to-peak deviation?
3-21. Under what conditions will the number of components (sidebands plus carrier) of an FM wave be the same as that of an a-m wave?
3-22. If the two sidebands of an a-m wave or those of an FM wave with a deviation ratio less than 1/2 are added, what is the name of the resultant signal that is the outcome of this addition?
3-23. What is the phase relationship between the double sideband and the center frequency component of:
a. An a-m wave?
b. An FM wave having a modulation index less than 1/2?
3-24. In brief, how can an indirect FM signal be obtained from an a-m signal?
3-25. Does the Armstrong system employ direct or indirect FM?
3-26. In the original Armstrong transmitter:
a. What stage is used to suppress the center frequency component of the a-m signal?
b. Why is the amplitude of the double sideband made much smaller than that of the carrier signal with which it is later combined?
3-27. If the initial peak phase swing of the original Armstrong transmitter was 8.5 degrees at a frequency of 75 cycles, what would be the equivalent peak frequency swing?
3-28. What is the purpose of the heterodyning system in the original Armstrong transmitter?
3-29. Why must the tuned circuits in the power output stages of FM transmitters be very broad as compared with those in a-m transmitters?