Filter Banks
Low bit-rate codecs often use an analysis filter bank to partition the wide audio band into smaller sub-bands; the decoder uses a synthesis filter bank to restore the sub-bands to a wide audio band. Uniformly spaced filter banks downconvert an audio band into a baseband, then lowpass filter and subsample the data. Transform-based filter banks multiply overlapping blocks of audio samples with a window function to reduce edge effects, and then perform a discrete transform such as DCT. Mathematically, the transforms used in codecs can be seen as filter banks, and sub-band filter banks can be seen as transforms.
Time-domain filter banks should provide ideal lowpass and highpass characteristics with a cutoff of fs/2, where fs is the sampling frequency; however, real filters have overlapping bands. For example, in a two-band system, the sub-band sampling rates must be decreased (2:1) to maintain the overall bit rate. This decimation introduces aliasing in the sub-bands. In the lower band, signals above fs/4 will alias to 0 to fs/4. In the upper band, signals below fs/4 alias up to fs/4 to fs/2. In the decoder, the sampling rate is restored (1:2) by adding zeros. Because of interpolation, in the lower band, signals from 0 to fs/4 will image around fs/4 into the upper band. Similarly, in the upper band, signals from fs/4 to fs/2 will image to the lower band.
Quadrature Mirror Filters
Generally, when N sub-bands are created, each sub-band is sub-sampled at 1/N to maintain an overall sampling limit.
We recall from Section 2, that the sampling frequency must be at least twice the bandwidth of a sampled signal. As noted, most filter banks do not provide ideal performance because of the finite width of their transition bands; the bands overlap, and the 1/N sub-sampling causes aliasing.
Clearly, bands that are spaced apart can avoid this, but will leave gaps in the signal's spectrum. Quadrature mirror filter (QMF) banks have the property of reconstructing the original signal from N overlapping sub-bands without aliasing, regardless of the order of the bandpass filters.
The aliasing components are exactly canceled, in the frequency domain, during reconstruction and the sub-bands are output in their proper place in frequency. The attenuation slopes of adjacent sub-band filters are mirror images of each other. Ideally, alias cancellation is perfect only if there is no requantization of the sub-band signals. A QMF is shown in FIG. 19. Intermediate samples can be critically sub-sampled without loss; if the input signal is split into N equal sub-bands, each sub-band can be sampled at 1/N; the sampling frequency for each sub-band filter is exactly twice the bandwidth of the filter. Generally, cascades of QMF banks may be used to create 4 to 24 sub-bands. By cascading some sub-bands unequally, relative bandwidths can be manipulated; delays are introduced to maintain time parity between sub-bands.
QMF banks can be implemented as symmetrical finite impulse-response filters with an even number of taps; the use of a reconstruction highpass filter with a z-transform of -H(-z) instead of H(-z) eliminates alias terms (when there is uniform quantizing in each sub-band). However, perfect reconstruction is generally limited to the case when N = 2, creating two equal-width sub-bands from one. These fs/2 sub-bands can be further divided by repeating the QMF process, and splitting each sub-band into two more sub-bands, each with a fs/4 sampling frequency. This can be accomplished with a tree structure; however, this adds delay to the processing. Other QMF architectures can be used to create multiple sub-bands with less delay. However, cascaded QMF banks suitable for multi-band computation needed for codec design suffer from long delay and high complexity. For that reason, many codecs use a pseudo QMF, also known as a polyphase filter, which offers a faster parallel approach that approximates the QMF. The QMF method is similar in concept to wavelet techniques.
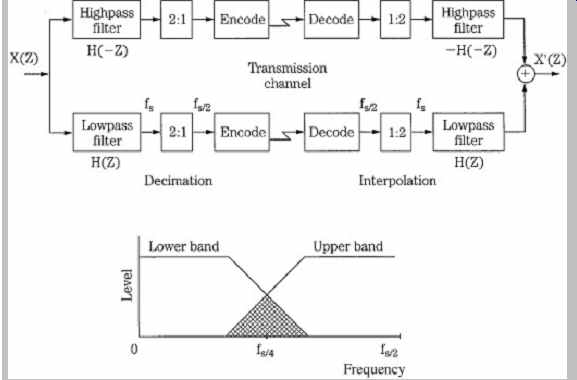
FIG. 19 A quadrature mirror filter forms two equal sub-bands. Alias components
introduced during decimation are exactly canceled during reconstruction. Multiple
QMF stages can be cascaded to form additional sub-bands.
Hybrid Filters
As noted, although filter banks with equally spaced bands are often used, they do not correlate well with the spacing of the ear's critical bands. Tree-structured filter banks can overcome this drawback. An example of a hybrid filter bank proposed by Karlheinz Brandenburg and James Johnston is shown in FIG. 20. It provides frequency analysis that corresponds more closely to critical-band spacing. Time domain samples are applied to an 80-tap QMF filter bank to yield four bands with bandwidths of 3 kHz, 6 kHz, and 12 kHz. The bands are applied to a 64-line transform that is sine-windowed with a 50% overlap. The output of 320 spectral components has a frequency resolution of 23.4 Hz at low frequencies and 187.5 Hz at high frequencies. A corresponding synthesis filter is used in the decoder.
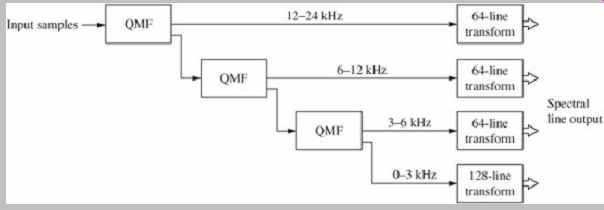
FIG. 20 A hybrid filter using a QMF filter bank and transforms to yield unequally
spaced spectral components. (Brandenburg and Johnston, 1990)
Polyphase Filters
A polyphase filter (also known as a pseudo-QMF or PQMF) yields a set of equally spaced bandwidth filters with phase interrelationships that permit very efficient implementation.
A polyphase filter bank can be implemented as an FIR filter that consolidates interpolation filtering and decimation. The different filters are generated from a single lowpass prototype FIR filter by modulating the prototype filter over different phases in time. For example, using a 512-tap FIR filter, each block of input samples uses 32 sets of coefficients to create 32 sub-bands, as shown in FIG. 21.
More generally, in an N-phase filter bank, each of the N sub-bands is decimated to a sampling frequency of 1/N. For every N input, the filter outputs one value in each sub-band.
In the first phase, the samples in an FIR transversal register and first-phase coefficients are used to compute the value in the first sub-band. In the second phase, the same samples in the register and second-phase coefficients are used to compute the value in the second sub-band, and so on. The impulse response coefficients in the first phase represent a prototype lowpass filter, and the coefficients in the other sub-band phases are derived from the prototype by multiplication with a cosine modulating function that shifts the low-pass response to each next bandpass center frequency. After N samples are output, the samples in the register are shifted by N, and the process begins again.
The center frequencies fc are given by:
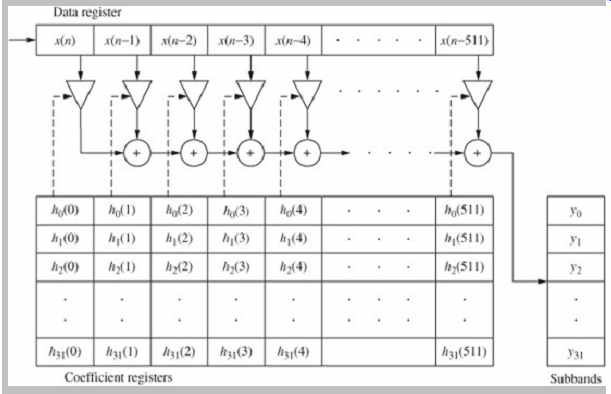
FIG. 21 A polyphase filter uses a single lowpass prototype FIR filter to
create sub-bands by modulating the prototype filter. This example shows a 512-tap
filter with 32 sets of 512 coefficients, yielding 32 sub-bands.
fc = ± fs(k + 1/2)/2N Hz
where fs is the sampling frequency and N is the number of sub-bands and k = 0, 1, 2, … , N-1.
Each sub-band has a bandwidth of fs/64. Polyphase filter banks offer good time-domain resolution, and good frequency resolution that can yield high stopband attenuation of 96 dB to minimize intraband aliasing. There is significant overlap in adjacent bands, but phase shifts in the cosine terms yield frequency-domain alias cancellation at the synthesis filter. The quantization process slightly degrades alias cancellation. The MPEG-1 and -2 standards specify a polyphase filter with QMF characteristics, operating as a block transform with N = 32 sub-bands and a 512-tap register. The flow chart of the MPEG-1 analysis filter and other details are given in Section 11. The particular analysis filter presented in the MPEG-1 standard requires approximately 80 real multiplies and 80 real additions for every output sample. Similarly, a polyphase synthesis filter is used in the decoder. The PQMF is a good choice to create a limited number of frequency bands. When higher-resolution analysis is needed, approaches such as an MDCT transform are preferred.
MDCT [modified discrete cosine transform]
The discrete Fourier transform (DFT) and discrete cosine transform (DCT) could be used in codecs to provide good frequency resolution. Also, the number of output points in the frequency domain equals the number of input samples in the time domain. However, to reduce blocking artifacts, an overlap-and-add of 50% doubles the number of frequency components relative to the number of time samples, and the DFT and DCT do not provide critical sampling. The increase in data rate is clearly counterproductive. The modified discrete cosine transform (MDCT) provides high-resolution frequency analysis and can allow a 50% overlap and provide critical sampling. As a result, it is used in many codecs.
The MDCT is an example of a time-domain aliasing cancellation (TDAC) transform in which only half of the frequency points are needed to reconstruct the time domain audio signal. Frequency-domain sub-sampling is performed; thus, a 50% overlap results in the same number of output points as input samples. Specifically, the length of the overlapping windows is twice that of the block time (shift length of the transform) resulting in a 50% overlap between blocks. Moreover, the overlap-and-add process is designed to cancel time-domain aliasing and allow perfect reconstruction. The MDCT also allows adaptability of filter resolution by changing the window length. Windows such as a sine taper and Kaiser-Bessel can be used. The MDCT also lends itself to adaptive window switching approaches with different window functions for the first and second half of the window; the time-domain aliasing property must be independently valid for each window half.
Many bands are possible with the MDCT with good efficiency, on the order of an FFT computation. The MDCT is also known as the modulated lapped transform (MLT).
As noted, a window function is applied to blocks of samples prior to transformation. I f a block is input to a filter bank without a window, it can be considered as a time limited signal with a rectangular window in which the samples in the block are multiplied by 1 and all other samples are multiplied by 0. The Fourier transform of this signal reveals that the sharp cutoff of the window's edges yields high-frequency content that would cause aliasing. To minimize this, a window can be applied that tapers the time-domain edge response down to zero. A window is thus a time function that is multiplied by an audio block to provide a windowed audio block. The window shape is selected to balance high-frequency resolution of the filter bank while minimizing spurious spectral components. The effect of the window must be compensated for to recover the original input signal after inverse-transformation. The overlap-and-add procedure accomplishes this by overlapping windowed blocks of the input signal and adding the result. The windows are designed specifically to allow this. Digital filters and windows are discussed in Section 17.
As noted, hybrid filter banks use a cascade of different filter types (such as polyphase and MDCT) to provide different frequency resolutions at different frequencies with moderate complexity. For example, MPEG-1 Layer III encoders use a hybrid filter with a polyphase filter bank and MDCT. The ATRAC algorithm is a hybrid codec that uses QMF to divide the signal into three sub-bands, and each sub-band is transformed into the frequency domain using the MDCT. Table 3 compares the properties of filter banks used in several low bit-rate codecs.
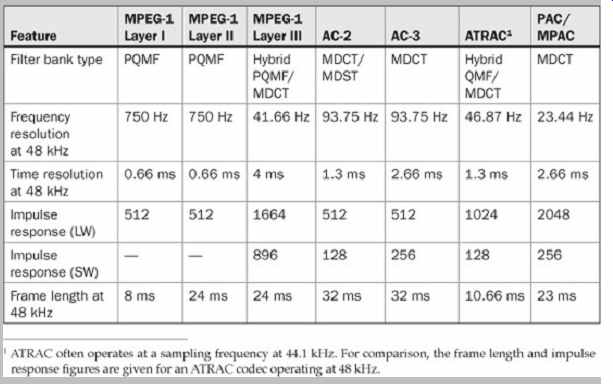
TABLE 3 Comparison of filter-bank properties (48-kHz sampling frequency).
(Brandenburg and Bosi, 1997)
Multichannel Coding
The problem of masking quantization noise is straightforward with a monaural audio signal; the masker and maskee are co-located. However, stereo and surround audio content also contain spatial localization cues. As a consequence, multichannel playback presents additional opportunities and obligations for low bit-rate algorithms. On one hand, for example, interchannel redundancies can be exploited by the coding algorithm to additionally and significantly reduce the necessary bit rate. On the other hand, great care must be taken because masking is spatially dependent. For example, quantization noise in one channel might be unmasked because its spatial placement differs from that of a masking signal in another channel. The human ear is fairly acute at spatial localization; for example, with the "cocktail-party effect" we are able to listen to one voice even when surrounded by a room filled with voices.
The unmasking problem is particularly challenging because most masking studies assume monaural channels where the masker and maskee are spatially equal. In addition, perceptual effects are very different for loudspeaker versus headphone playback.
At frequencies above 2 kHz, within critical bands, we tend to localize sounds based on the temporal envelope of the signal rather than specific temporal details. Coding artifacts must be concealed in time and frequency, as well as in space. If stereo channels are improperly coded, coding characteristics of one channel might interfere with the other channel, creating stereo unmasking effects. For example, if a masking sum or difference signal is incorrectly processed in a matrixing operation and is output in the wrong channel, the noise in its original channel that it was supposed to mask might become audible.
Dual-mono coding uses two codecs operating independently. Joint-mono coding uses two monophonic codecs but they operate under the constraint of a single bit rate. Independent coding of multiple channels can create coding artifacts. For example, quantization noise might be audibly unmasked because it does not match the spatial placement of a stereo masking signal. Multichannel coding must consider subtle changes in the underlying psychoacoustics. For example, with the binaural masking level difference (BMLD) phenomenon, the masking threshold can be lower when listening with two ears, instead of one. At low frequencies (below 500 Hz), differences in phase between the masker and maskee at two ears can be readily audible.
Joint-stereo coding techniques use interchannel properties to take advantage of interchannel redundancy and irrelevance between stereo (or multiple) channels to increase efficiency. The data rate of a stereo signal is double that of a monaural signal, but most stereo programs are not dual-mono. For example, the channels usually share some level and phase information to create phantom images. This interchannel correlation is not apparent in the time domain, but it is readily apparent when analyzing magnitude values in the frequency domain. Joint-stereo coding codes common information only once, instead of twice as in left/right independent coding. A 256-kbps joint stereo coding channel will perform better than two 128 kbps channels.
Many multichannel codecs use M/S (middle/side) coding of stereo signals to eliminate redundant monaural information. Coding efficiency can be high particularly with near-monaural signals and the technique performs well when there is a BMLD. With the M/S technique, rather than code discrete left and right channels, it is more efficient to code the middle (sum) and side (difference) signals using a matrix in either the time or frequency domains. The decoder uses reverse processing. In a multichannel codec, M/S coding can be applied to channel pairs placed left/right symmetrically to the listener. This configuration helps to avoid spatial unmasking.
As an alternative to M/S coding, intensity stereo coding (also known as dynamic crosstalk or channel coupling) can be used. High frequencies are primarily perceived as energy-time envelopes. With the intensity stereo technique, the energy-time envelope is coded rather than the waveform itself. One set of values can be efficiently coded and shared among multiple channels. Envelopes of individual channels can be reconstructed in the decoder by individually applying proper amplitude scaling. The technique is particularly effective at coding spatial information. In some codecs, different joint-stereo coding techniques are used in different spectral areas.
Using diverse and dynamically changing psychoacoustic cues and signal analysis, inaudible components can be removed with acceptable degradation. For example, a loud sound in one loudspeaker channel can mask other softer sounds in other channels. Above 2 kHz, localization is achieved primarily by amplitude; because the ear cannot follow fast individual waveform cycles, it tracks the envelope of the signal, not its phase. Thus the waveform itself becomes less critical; this is intensity localization. In addition, the ear is limited in its ability to localize sounds close in frequency. To convey a multichannel surround field, the high frequencies in each channel can be divided into bands and combined band by band into a composite channel. The bands of the common channel are reproduced from each loudspeaker, or panned between loudspeakers, with the original signal band envelopes. Use of a composite channel achieves data reduction. In addition, other masking principles can be applied prior to forming the composite channel. Many multichannel systems use a 5.1 format with three front channels, two independent surround channels, and a subwoofer channel. Very generally, the number of bits required to code a multichannel signal is proportional to the square root of the number of channels. A 5.1-channel codec, for example, would theoretically require only 2.26 times the number of bits needed to code one channel.
Tandem Codecs
In many applications, perceptual codecs will be used in tandem (cascaded). For example, a radio station may receive a coded signal, decode it to PCM for mixing, cross-fading, and other operations, and then code it again for broadcast, where it is decoded by the consumer, who may make a coded recording of it. In all, many different coding processes may occur. As the signal passes through this chain, coding artifacts will accumulate and can become audible. The nature of the signal degrades the ability of subsequent codecs to suitably model the signal. Each codec will quantize the audio signal, adding to the quantization noise already permitted by previous encoders.
Because many psychoacoustic models monitor the audio masking levels and not the underlying noise, noise can be allowed to rise to the point of audibility. Furthermore, when noise reaches audibility, the codec may allocate bits to code it, thus robbing bits needed elsewhere; this can increase noise in other areas.
In addition, tandem codecs are not necessarily synchronized, and will delineate audio data frames differently. This can yield audible noise-like artifacts and pre-echoes in the signal. When codecs are cascaded, it is important to begin with the highest-quality coding possible, then step down. A low-fidelity link will limit all subsequent processing. Highest-quality codecs have a high coding margin between the masking threshold, and coding noise; they tolerate more coding generations.
To reduce degradation caused by cascading, researchers are developing "inverse decoders" that analyze a decoded low bit-rate bitstream and extract the encoding parameters used to encode it. If the subsequent encoder is given the relevant coding decisions used by the previous encoder, and uses the same quantization parameters, the signal can be re-encoded very accurately with minimal loss compared to the first-generation coded signal. Conceivably, aspects such as type of codec, filter bank type, framing, spectral quantization, and stereo coding parameters can be extracted. Further, such systems could use the extracted parameters to ideally re-code the signal to its original bitstream representation, thus avoiding the distortion accumulated by repeatedly encoding/decoding content through the cascades in a signal chain. Some systems would accomplish this analysis and reconstruction task using only the decoded audio bitstream.
In some codec designs, metadata, sometimes called "mole" data because it is buried data that can burrow through the signal chain, is embedded in the audio data using steganographic means. Mole data such as header information, frame alignment, bit allocation, and scale factors may be conveyed. The mole data helps ensure that cascading does not introduce additional distortion. Ideally, the auxiliary information allows subsequent codecs to derive all the encoding parameters originally used in the first-generation encoding. This lets downstream tandem codecs apply the same framing boundaries, psychoacoustic modeling, and quantization processing as upstream stages. It is particularly important for the inverse decoder to use the same frame alignment as the original encoder so that the same sets of samples are available for processing.
With correct parameters, the cascaded output coded bitstream may be nearly identical to the input coded bitstream, within the tolerances of the filter banks. In another effort to reduce the effects of cascading, some systems allow operations to take place on the signal in the codec domain, without need for intermediate decoding to PCM and re-encoding. Such systems may allow gain changing, fade-in and fade-outs, cross-fading, equalization, transcoding to a higher or lower bit rate, and transcoding to a different codec, as the signal passes through a signal chain.
Spectral Band Replication
Any perceptual codec must balance audio bandwidth, bit rate, and audible artifacts. By reducing coded audio bandwidth, relatively more bits are available in the remaining bandwidth. Spectral band replication (SBR) allows the underlying codec to reduce bit rate through bandwidth reduction, while providing bandwidth extension at the decoder. Spectral band replication is primarily a postprocess that occurs at the receiver. It extends the high frequency range of the audio signal at the receiver. The lower part of the spectrum is transmitted. Higher frequencies are reconstructed by the SBR decoder based on the lower transmitted frequencies and control information. The replicated high-frequency signal is not analytically coherent compared to the baseband signal, but is coherent in a psychoacoustic sense; this is assisted by the fact that the ear is relatively less sensitive to variations at high frequencies.
The codec operates at half the nominal sampling frequency while the SBR algorithm operates at the full sampling frequency. The SBR encoder precedes the waveform encoder and uses QMF analysis and energy calculations to extract information that describes the spectral envelope of the signal by measuring energy in different bands. This process must be uniquely adaptive to its time and frequency analysis. For example, a transient signal might exhibit significant energy in the high band, but much less in the low band that will be conveyed by the codec and used for replication. The encoder also compares the original signal to the signal that the decoder will replicate. For example, tonal and nontonal aspects and the correlation between the low and high bands are analyzed. The encoder also considers what frequency ranges the underlying codec is coding. To assist the processing, control information is transmitted by the encoded bitstream at a very low bit rate. SBR can be employed for monaural, stereo, or multichannel encoding.
The SBR decoder follows the waveform decoder and uses the time-domain signal decoded by the underlying codec. This lowpass data is upsampled and applied to a QMF analysis filter bank and its sub-band signals (perhaps 32) are used for high-band replication based on the control information. In addition, the replicated high-band data is adaptively filtered and envelopment adjustment is applied to achieve suitable perceptual characteristics. The delayed low-band and high-band sub-bands are applied to a synthesis filter bank (perhaps 64 bands) operating at the SBR sampling frequency. In some cases, the encoder measures stereo correlation in the original signal and the decoder generates a corresponding pseudo-stereo signal.
Replicated spectral components must be harmonically related to the baseband components to avoid dissonance.
At low and medium bit rates, SBR can improve the efficiency of a perceptual codec by as much as 30%. The improvement depends on the type of codec used. For example, when SBR is used with MP3 (as in MP3PRO), a 64-kbps stereo stream can achieve quality similar to that of a conventional MP3 96-kbps stereo stream. Generally, SBR is most effective when the codec bit rate is set to provide an acceptable level of artifacts in the restricted bandwidth. MP3PRO uses SBR in a backward- and forward-compatible way. Conventional MP3 players can decode an MP3PRO bitstream (without SBR) and MP3PRO decoders can decode MP3 and MP3PRO streams. SBR techniques can also be applied to Layer II codecs and MPEG-4 AAC codecs; the latter application is called High-Efficiency AAC (HE AAC) and aacPlus.
Low-complexity SBR can be accomplished with "blind" processing in which the decoder is not given control information. A nonlinear device such as a full-wave rectifier is used to generate harmonics, a filter selects the needed part of the signal, and gain is adjusted. This method assumes correlation between low- and high-frequency bands, thus its reconstruction is relatively inexact. Other SBR methods may extend low-frequency audio content by generating subharmonics, for example, in a voice signal passing through a telephone system that is bandlimited at low frequencies (as well as high frequencies). Other SBR methods are specifically designed to enhance sound quality through small loudspeakers. For example, a system might shift un-reproducible low frequencies to higher frequencies above the speaker's cutoff, and rely on psycho-acoustic effects such as residue pitch and virtual pitch to create the impression of low-frequency content.
Perceptual Coding Performance Evaluation
Whereas traditional audio coding is often a question of specifications and measurements, perceptual coding is one of physiology and perception. With the advent of digital signal processing, audio engineers can design hardware and software that "hears" sound the same way that humans hear sound.
The question of how to measure the sonic performance of perceptual codecs raises many issues that were never faced by traditional audio systems. Linear measurements might reveal some limitations, but cannot fully penetrate the question of the algorithm's perceptual accuracy. For example, a narrow band of noise introduced around a tone might not be audible, broadband white noise at the same energy would be plainly audible, but both would provide the same signal-to-noise measurement. Demonstrations of the so-called "13-dB miracle" by James Johnston and Karlheinz Brandenburg showed how noise that is shaped to hide under a narrow-band audio signal can be just barely noticeable or inaudible, yet the measured signal-to-noise ratio is only 13 dB. However, a wideband noise level with an S/N ratio of 60 dB in the presence of the same narrow band audio signal would be plainly audible. As another example, a series of sine tones might provide a flat frequency response in a perceptual codec because the tones are easily coded. However, a broadband complex tone might be coded with a signal-dependent response.
Traditional audio devices are measured according to their small deviations from linearity. Perceptual codecs are highly nonlinear, as is their model, the human ear. The problem of how to determine the audibility of quantization noise levels and coding artifacts is not trivial. Indeed, the entire field of psychoacoustics must wrestle with the question of whether any objective or subjective measures can wholly quantify how an audible event affects a complex biological system-that is, a listener.
It is possible to non-quantitatively evaluate reduction artifacts using simple test equipment. A sine-wave oscillator can output test tones at a variety of frequencies; a dual-trace oscilloscope can display both the uncompressed and compressed waveforms. The waveforms should be time-aligned to compensate for processing delay in the codec. With a 16-bit system, viewed at 2 V peak-to-peak, one bit represents 30 µV. Any errors, including wideband noise and harmonic distortion at the one-bit level, can be observed. The idle channel signal performance can be observed with the coded output of a zero input signal; noise, error patterns, or glitches might appear. It also might be instructive to examine a low-level signal (0.1 V). In addition, a maximum level signal can be used to evaluate headroom at a variety of frequencies. More sophisticated evaluation can be performed with distortion and spectrum analyzers, but analysis is difficult. For example, traditional systems can be evaluated by measuring total harmonic distortion and noise (THD + N or SINAD) but such measurements are not meaningful for perceptual codecs.
FIG. 22 shows the spectral analysis of a 16-bit linear recorder and a 384-kbps perceptual recorder. When encoding a simple sine wave, although the perceptual codec adds noise within its masking curve around the tone, it easily codes the signal with low distortion. When using more complex stimuli, a perceptual codec will generate high distortion and noise measurements as anticipated by its inherent function. But, such measurements have little correlation to subjective performance. Clearly, traditional test tones and measurements are of limited use in evaluating perceptual codecs.
Richard Cabot devised a test that perceptually compares the codec output with a known steady-state test signal. A multi-tone signal is applied to the codec; the output is transformed into the frequency domain with FFT, and applied to an auditory model to estimate masking effects of the signal. Because the spectrum of the test signal is known, any error products can be identified and measured. In particular, the error signal can be compared to internally modeled masking curves to estimate audibility.
The NMR of the error signal level and masking threshold can be displayed as a function of frequency.
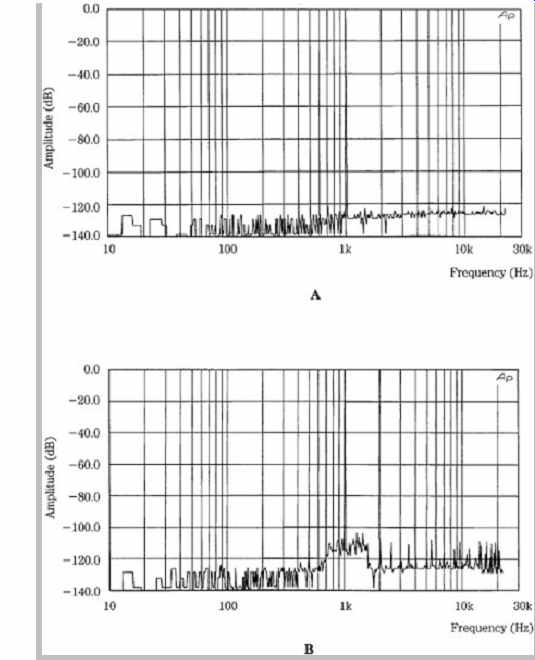
FIG. 22 Spectral analysis of a single 1-kHz test tone reveals little about
the performance of a perceptual codec. A. Analysis of a 16-bit linear PCM signal
shows a noise floor that is 120 dB below signal. B. Analysis of a 384-kbps perceptually
coded signal shows a noise floor that is 110 dB below signal with a slightly
increased noise within the masking curve.
For example, FIG. 23A shows a steady-state test of a codec. The multi-tone signal consists of 26 sine waves distributed logarithmically across the audio spectrum, approximately one per critical band with a gap to allow for analysis of residual noise and distortion. It is designed to maximally load the codec's sub-bands, and consume its available bit rate. The figure shows the modeled masking curve based on the multi-tone, and distortion produced by the codec, consisting of quantization error, intermodulation products, and noise sidebands. In FIG. 23B, the system has also integrated the distortion and noise products across the critical bandwidth of the human ear to simulate a perceived distortion level. Distortion products above the model's masking curve might be audible, depending on ambient listening conditions. In this case, some distortion might be audible at low levels. Clearly, evaluation of results depends on the sophistication of the analyzer's masking model. Multichannel test tones can be used to analyze interchannel performance, for example, to determine how high frequency information is combined between channels.
This particular test does not evaluate temporal artifacts.

FIG. 23 A multi-tone test signal is designed to deplete the bit capacity
of a perceptual codec, emulating the action of a complex musical tone. A. Analysis
shows the output test tone and the composite masking curve calculated by the
testing device. B. The testing device computes the composite distortion in
critical bands. Distortion above the calculated masking threshold might be
audible.
Theoretically, the best objective testing means for a perceptual codec is an artificial ear. To measure perceived accuracy, the algorithm contains a model that emulates the human hearing response. The measuring model can identify defects in the codec under test. A noise-to-mask ratio (NMR) can estimate the coding margin (see FIG. 11). The original signal (appropriately delayed) and the error signal (the difference between the original and coded signals) are independently subjected to FFT analysis, and the resulting spectra are divided into sub-bands. The masking threshold (maximum masked error energy) in each original signal sub-band is estimated. The actual error energy in each coded signal sub-band is determined and compared to the masking threshold. The ratio of error energy to masking threshold is the NMR in each sub-band.
A positive NMR would indicate an audible artifact. The NMR values can be linearly averaged and expressed in dB.
This mean NMR measures remaining audibility headroom in the coded signal. NMR can be plotted over time to identify areas of coding difficulty. A masking flag, generated when the NMR exceeds 0 dB in a sub-band (artifact assumed to be audible) can be used to measure the number of impairments in a coded signal. A relative masking flag counts the number of impairments normalized over a number of blocks and sub-bands.
The ITU-R (International Telecommunication Union-Radio communication Bureau) Task Group 10/4 developed standardized objective perceptual measurement techniques that are described in a system called Perceptual Evaluation of Audio Quality (PEAQ). This system uses a multimode technique to compare an original signal to a processed signal and assess the perceived quality of the processed signal. Both signals are represented within an artificial ear and perceptually relevant differences are extracted and used to compute a quality measure. The standard describes both an FFT-based, and a filter bank-based ear algorithm; a simple implementation uses only the FFT-based model, while an advanced implementation uses elements of both. The system can evaluate criteria such as loudness of linear and nonlinear distortion, harmonic structure, masking ratios, and changes in modulation. For example, an NMR can specify the distance between a coded signal's error energy and the masked threshold. Mapping variables by a neural network yields quality measures that accurately correlate to the results of human testing. PEAQ is described in ITU-R Recommendation BS.1387-1, "Method for Objective Measurements of Perceived Audio Quality." Use of an artificial ear to evaluate codec performance is limited by the quality of the reference model used in the ear.
The codec's performance can only be as good as the artificial ear itself. Thus, testing with an artificial ear is inherently paradoxical. A reference ear that is superior to that in the psychoacoustic model of the codec under test would ideally be used to replace that in the codec. When the codec is supplied with the reference model, the codec could achieve "perfect" performance. Moreover, the criteria used in any artificial ear's reference model are arbitrary and inherently subjective because they are based on the goals of its designers.
Critical Listening
Ultimately, the best way to evaluate a perceptual codec is to exhaustively listen to it, using a large number of listeners.
This kind of critical listening, when properly analyzed by objective means, is the gold standard for codec evaluation.
In particular, the listening must be blind and use expert listeners, and appropriate statistical analysis must be performed to provide statistically confident results.
When a codec is not transparent, artifacts such as changes in timbre, bursts of noise, granular ambient sound, shifting in stereo imaging, and spatially unmasked noise can be used to identify the "signature" of the codec.
Bandwidth reduction is also readily apparent, but a constant bandwidth reduction is less noticeable than a continually changing bandwidth. Changes in high-frequency content, such as from coefficients that come and go in successive transform blocks, create artifacts that are sometimes called "birdies." Speech is often a difficult test signal because its coding requires high resolution in both time and frequency. With low bit rates or long transform windows, coded speech can assume a strangely reverberant quality. A stereo or surround recording of audience applause sometimes reveals spatial coding errors. Sub-band codecs can have unmasked quantization noise that appears as a burst of noise in a processing block. In transform codecs, errors are reconstructed as basis functions (for example, a windowed cosine) of the codec's transform. A codec with a long block length can exhibit a pre-echo burst of noise just before a transient, or there might be a tinkling sound or a softened attack.
Transform codec artifacts tend to be more audible at high frequencies. Changes in high-frequency bit allocation can result in a swirling sound due to changes in high-frequency timbre. In many cases, artifacts are discerned only after repeated listening trials, for example, after a codec has reached the marketplace.
For evaluation purposes, audio fidelity can be considered in four categories:
• Large Impairments. These sound quality differences are readily audible to even untrained listeners. For example, two identical speaker systems, one with normal tweeters and the other with tweeters disabled, would constitute a large impairment.
• Medium Impairments. These sound quality differences are audible to untrained listeners but may require more than casual listening. The ability to readily switch back and forth and directly compare two sources makes these impairments apparent. For example, stereo speakers with a midrange driver wired out of phase would constitute a medium impairment.
• Small Impairments. These sound quality differences are audible to many listeners, however, some training and practice may be necessary. For example, the fidelity difference between a music file coded at 128 kbps and 256 kbps, would reveal small impairments in the 128-kbps file. Impairments may be unique and not familiar to the listener, so they are more difficult to detect and take longer to detect.
• Micro Impairments. These sound quality differences are subtle and require patient listening by trained listeners over time. In many cases, the differences are not audible under normal listening conditions, with music played at normal levels. It may be necessary to amplify the music, or use test signals such as low-level sine tones and dithered silence. For example, slightly audible distortion on a -90 dBFS 1 kHz dithered sine wave would constitute a micro impairment.
When listening to large impairments such as from loudspeakers, audio quality evaluations can rely on familiar objective measurements and subjective terms to describe differences and find causes for defects. However, when comparing higher-fidelity devices such as codecs, smaller impairments are considerably more difficult to quantify. It is desirable to have methodologies to identify, categorize, and describe these subtle differences. Developing these will require training of critical listeners, ongoing listening evaluations, and discussions among listeners and codec designers to "close the loop." Further, to truly address the task, it will be necessary to systematically find thresholds of audibility of various defects. This search would introduce known defects and then determine the subjective audibility of the defects and thresholds of audibility.
It is desirable to correlate subjective impressions of listeners with objective design parameters. This would allow designers to know where audio fidelity limitations exist and thus know where improvements can be made.
Likewise, this knowledge would allow bit rates to be lowered while knowing the effects on fidelity. There must be agreement on definitions of subjective terminology. This would provide language for listeners to use in their evaluations, it would bring uniformity to the language used by a broad audience of listeners, and it would provide a starting point in the objective qualification of their subjective comments.
The Holy Grail of subjective listening is the correlation between the listener's impressions, and the objective means to measure the phenomenon. This is a difficult problem. The reality is that correlations are not always known. The only way to correlate subjective impressions with objective data is with research-in particular, through critical listening. Over time, it is possible that patterns will emerge that will provide correlation. While correlation is desirable, critical listening continues to play an important role without it.
It is worth noting that within a codec type, for example, with MP3 codecs, the MPEG standard dictates that all compliant decoders should perform identically and sound the same. It is the encoders that may likely introduce sonic differences. However, some decoders may not properly implement the MPEG standard and thus are not compliant.
For example, they may not support intensity stereo coding or variable rate bitstream decoding. MP3 encoders, for example, can differ significantly in audio performance depending on the psychoacoustic model, tuning of the nested iteration loops, and strategy for switching between long and short windows. Another factor is the joint-stereo coding method and how it is optimized for a particular number of channels, audio bandwidth and bit rate. Many codecs have a range of optimal bit rates; quality does not improve significantly above those rates, and quality can decrease dramatically below them. For example, MPEG Layer III is generally optimized for a bit rate of 128 kbps for a stereo signal at 48 kHz (1.33 bit/sample) whereas AAC is targeted at a bit rate of 96 kbps (1 bit/sample).
When differences between devices are small, one approach is to study the residue (difference signal) between them. The analog outputs could be applied to a high-quality A/D converter; one signal is inverted; the signals are precisely time-aligned with bit accuracy; the signals are added (subtracted because of inversion); and then the residue signal may be studied.
Expert listeners are preferred over average listeners because experts are more familiar with peculiar and subtle artifacts. An expert listener more reliably detects details and impairments that are not noticed by casual listeners.
Listeners in any test should be trained on the testing procedure and in particular should listen to artifacts that the codec under test might exhibit. For example, listeners might start their training with very low bit-rate examples or left-minus-right signals, or residue signals with exposed artifacts so they become familiar with the codec's signature. It is generally felt that a 16-bit recording is not an adequate reference when testing high-quality perceptual codecs because many codecs can outperform the reference. The reference must be of the highest quality possible.
Many listening tests are conducted using high-quality headphones; this allows critical evaluation of subtle audible details. When closed-ear headphones are used, external conditions such as room acoustics and ambience noise can be eliminated. However, listening tests are better suited for loudspeaker playback. For example, this is necessary for multichannel evaluations. When loudspeaker playback is used, room acoustics play an important role in the evaluation. A proper listening room must provide suitable acoustics and also provide a low-noise environment including isolation from external noise. In some cases, rooms are designed and constructed according to standard reference criteria. Listening room standards are described below.
To yield useful conclusions, the results of any listening test must be subjected to accepted statistical analysis. For example, the ANOVA variance model is often used. Care must be taken to generate a valid analysis that has appropriate statistical significance. The number of listeners, the number of trials, the confidence interval, and other variables can all dramatically affect the validity of the conclusions. In many cases, several listening tests, designed from different perspectives, must be employed and analyzed to fully determine the quality of a codec.
Statistical analysis is described next.