|
|
In many ways, digital signal processing (DSP) returns us to the elemental beginning of our discussion of digital audio.
Although conversion, error correction, data reduction, and other concerns can be critical to a digitization system, it is the software-driven signal processing of digital audio data that is germane to the venture. Without the ability to manipulate the numbers that comprise digital audio data, its digitization would not be useful for many applications.
Moreover, a discussion of digital signal processing returns us to the roots of digital audio in that the technology is based on the same elemental mathematics that first occupied us. On the other hand, digital signal processing is a science far removed from simple logic circuits, with sophisticated algorithms required to achieve its aim of efficient signal manipulation. Moreover, digital signal processing may demand very specialized hardware devices for successful operation.
Fundamentals of Digital Signal Processing
Digital signal processing is used to generate, analyze, alter, or otherwise manipulate signals in the digital domain.
It is based on sampling and quantization, the same principles that make digital recording possible. However, instead of providing a storage or transmission means, it is a processing method. DSP is similar to the technology used in computers and microprocessor systems. However, whereas a regular computer processes data, a DSP system processes signals. In particular, a digital audio signal is a time-based sequence in which the ordering of values is critical. A digital audio signal only makes sense, and can be processed properly, if the sequence is properly preserved. DSP is thus a special application of general data processing. Simply stated, DSP uses a mathematical formula or algorithm to change the numerical values in a bitstream signal.
A signal can be any natural or artificial phenomenon that varies as a function of an independent variable. For example, when the variable is time, then changes in barometric pressure, temperature, oil pressure, current, or voltage are all signals that can be recorded, transmitted, or manipulated either directly or indirectly. Their representation can be either analog or digital in nature, and both offer advantages and disadvantages.
Digital processing of acquired waveforms offers several advantages over processing of continuous-time signals.
Fundamentally, the use of unambiguous discrete samples promotes: the use of components with lower tolerances; predetermined accuracy; identically reproducible circuits; a theoretically unlimited number of successive operations on a sample; and reduced sensitivity to external effects such as noise, temperature, and aging. The programmable nature of discrete-time signals permits changes in function without changes in hardware. Digital integrated circuits are small, highly reliable, low in cost, and capable of complex processing. Some operations implemented with digital processing are difficult or impossible with analog means.
Examples include filters with linear phase, long-term uncorrupted memory, adaptive systems, image processing, error correction, data reduction, data compression, and signal transformations. The latter includes time domain to frequency-domain transformation with the discrete Fourier transform (DFT) and special mathematical processing such as the fast Fourier transform (FFT).
On the other hand, DSP has disadvantages. For example, the technology always requires power; there is no passive form of DSP circuitry. DSP cannot presently be used for very high frequency signals. Digital signal representation of a signal may require a larger bandwidth than the corresponding analog signal. DSP technology is expensive to develop. Circuits capable of performing fast computation are required. Finally, when used for analog applications, analog-to-digital (A/D) and digital-to-analog (D/A) conversion are required. In addition, the processing of very weak signals such as antenna signals or very strong signals such as those driving a loudspeaker, presents difficulties; digital signal processing thus requires appropriate amplification treatment of the signal.
DSP Applications
In the 1960s, signal processing relied on analog methods; electronic and mechanical devices processed signals in the continuous-time domain. Digital computers generally lacked the computational capabilities needed for digital signal processing. In 1965, the invention of the fast Fourier transform to implement the discrete Fourier transform, and the advent of more powerful computers, inspired the development of theoretical discrete-time mathematics, and modern DSP.
Some of the earliest uses of digital signal processing included soil analysis in oil and gas exploration, and radio and radar astronomy, using mainframe computers. With the advent of specialized hardware, extensive applications in telecommunications were implemented including modems, data transfer between computers, and vocoders and transmultiplexers in telephony. Medical science uses digital signal processing in processing of X-ray and NMR (nuclear magnetic resonance) images. Image processing is used to enhance photographs received from orbiting satellites and deep-space vehicles. Television studios use digital techniques to manipulate video signals. The movie industry relies on computer-generated graphics and 3D image processing. Analytical instruments use digital signal transforms such as FFT for spectral and other analysis. The chemical industry uses digital signal processing for industrial process control. Digital signal processing has revolutionized professional audio in effects processing, interfacing, user control, and computer control. The consumer sees many applications of digital signal processing in the guise of personal computers, cell phones, gaming consoles, MP3 players, DVD and Blu-ray players, digital radio receivers, HDTV receivers and displays, and many other devices.
DSP presents rich possibilities for audio applications.
Error correction, multiplexing, sample rate conversion, speech and music analysis and synthesis, data reduction and data compression, filtering, adaptive equalization, dynamic compression and expansion, reverberation, ambience processing, time alignment, acoustical noise cancellation, mixing and editing, encryption and watermarking, and acoustical analysis can all be performed with digital signal processing.
Discrete Systems
Digital audio signal processing is concerned with the manipulation of audio samples. Because those samples are represented as numbers, digital audio signal processing is thus a science of calculation. Hence, a fundamental understanding of audio DSP must begin with its mathematical essence.
When the independent variable, such as time, is continuously variable, the signal is defined at every real value of time (t). The signal is thus a continuous time-based signal. For example, atmospheric temperature changes continuously throughout the day. When the signal is only defined at discrete values of time (nT), the signal is a discrete time signal. A record of temperature readings throughout the day is a discrete time signal. As we observed in Section 2, using the sampling theorem, any bandlimited continuous time function can be represented without theoretical loss as a discrete time signal. Although general discrete time signals and digital signals both consist of samples, a general discrete time signal can take any real value but a digital signal can only take a finite number of values. In digital audio, this requires an approximation using quantization.
Linearity and Time-Invariance
A discrete system is any system that accepts one or more discrete input signals x(n) and produces one or more discrete output signals y(n) in accordance with a set of operating rules. The input and output discrete time signals are represented by a sequence of numbers. If an analog signal x(t) is sampled every T seconds, the discrete time signal is x(nT), where n is an integer. Time can be normalized so that the signal is written as x(n).
Two important criteria for discrete systems are linearity and time-invariance. A linear system exhibits the property of superposition: the response of a linear system to a sum of signals is the sum of the responses to each individual input. That is, the input x1(n) + x2(n) yields the output y1(n) + y2(n). A linear system exhibits the property of homogeneity:
the amplitude of the output of a linear system is proportional to that of the input. That is, an input ax(n) yields the output ay(n). Combining these properties, a linear discrete system with the input signal ax1(n) + bx2(n) produces an output signal ay1(n) + by2(n) where a and b are constants. The input signals are treated independently, the output amplitude is proportional to that of the input, and no new signal components are introduced. As described in the following paragraphs, all z-transforms and Fourier transforms are linear.
A discrete time system is time-invariant if the input signal x(n - k) produces an output signal y(n - k) where k is an integer. In other words, a linear time-invariant discrete (LTD) system behaves the same way at all times; for example, an input delayed by k samples generates an output delayed by k samples.
A discrete system is causal if at any instant the output signal corresponding to any input signal is independent of the values of the input signal after that instant. In other words, there are no output values before there has been an input signal. The output does not depend on future inputs.
As some theorists put it, a causal system doesn't laugh until after it has been tickled.
Impulse Response and Convolution
The impulse response is an important concept in many areas, including digital signal processing. The impulse response h(n) gives a full description of a linear time invariant discrete system in the time domain. An LTD system, like any discrete system, converts an input signal into an output signal, as shown in FIG. 1A. However, an LTD system has a special property such that when an impulse (a delta function) is applied to an LTD system, the output is the system's impulse response, as shown in Fig. 1B. The impulse response describes the system in the time domain, and can be used to reveal the frequency response of the system in the frequency domain. Practically speaking, most digital filters are LTD systems, and yield this property. A system is stable if any input signal of finite amplitude produces an output signal of finite amplitude. In other words, the sum of the absolute value of every input and the impulse response must yield a finite number. Useful discrete systems are stable.
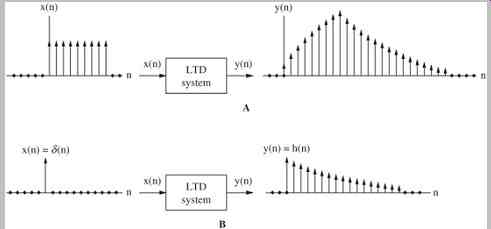
FIG. 1 Two properties of linear time-invariant discrete (LTD) systems. A.
LTD systems produce an output signal based on the input. B. LTD systems can
be characterized by their impulse response, the output from a single pulse
input.
Furthermore, the sampled impulse response can be used to filter a signal. Audio samples themselves are impulses, represented as numbers. The signal could be filtered, for example, by using the samples as scaling values; all of the values of a filter's impulse response are multiplied by each signal value. This yields a series of filter impulse responses scaled to each signal sample. To obtain the result, each scaled filter impulse response is substituted for its multiplying signal sample. The filter response can extend over many samples; thus, several scaled values might overlap. When these are added together, the series of sums forms the new filtered signal values.
This is the process of convolution. The output of a linear system is the convolution of the input and the system's impulse response. Convolution is a time-domain process that is equivalent to the multiplication of the frequency responses of two networks. Convolution in the time domain is equivalent to multiplication in the frequency domain.
Furthermore, the duality exists such that multiplication in the time domain is equivalent to convolution in the frequency domain.
Fundamentally, in convolution, samples (representing the signal at different sample times) are multiplied by weighting factors. These products are continually summed together to produce an output. A finite impulse response (FIR) oversampling filter (as described in Section 4) provides a good example. A series of samples are multiplied by the coefficients that represent the impulse response of the filter, and these products are summed. The input time function has been convolved with the filter's impulse in the time domain. For example, the frequency response of an ideal lowpass filter can be achieved by using coefficients representing a time-domain sin(x)/x impulse response. The convolution of the input signal with coefficients results in a filtered output signal.

FIG. 2 Convolution can be performed by folding, shifting, multiplying, and
adding number sequences to generate an ordered weighted product.
Recapitulating, the response of a linear and time invariant system (such as a digital filter) over all time to an impulse is the system's impulse response; its response to an amplitude scaled input sample is a scaled impulse response; its response to a delayed impulse is a delayed impulse response. The input samples are composed of a sequence of impulses of varying amplitude, each with a unique delay. Each input sample results in a scaled, time delayed impulse response. By convolution, the system's output at any sample time is the sum of the partial impulse responses produced by the scaled and shifted inputs for that instant in time.
Because convolution is not an intuitive phenomenon, some examples might be useful. Mathematically, convolution expresses the amount of overlap of one function as it is shifted over another function. Suppose that we want to convolve the number sequence 0.5,0.5,0.5 (representing an audio signal) with 4,3,2 (representing an impulse response). We reverse the order of the second sequence to 2,3,4 and shift the sequence through the first sequence, multiplying common pairs of numbers and adding the totals, as shown in FIG. 2. The resulting values are the convolution sum and define the output signal at sample times.
To illustrate this using discrete signals, consider a network that produces an output h(n) when a single waveform sample is input (refer to FIG. 1B). The output h(n) defines the network; from this impulse response we can find the network's response to any input. The network's complete response to the waveform can be found by adding its response to all of the individual sample responses. The response to the first input sample is scaled by the amplitude of the sample and is output time invariantly with it. Similarly, the inputs that follow produce outputs that are scaled and delayed by the delay of the input. The sum of the individual responses is the full response to the input waveform:
This is convolution, mathematically expressed as:
y(n) = x(n) * h(n) = h(n) * x(n)
where * denotes the convolution sum.
The output signal is the convolution of the input signal with the system's impulse response. A convolution sum can be graphically evaluated by a process of folding, translating, multiplying, and shifting. The signal x(n) is the input to a linear shift invariant system characterized by the impulse response h(n), as shown in FIG. 3A. We can convolve x(n) with h(n) to find the output signal y(n). Using convolution graphically, we first fold h(n) to time-reverse it as shown in FIG. 3B. Folding is necessary to yield the correct time-domain response as we move the impulse response from left to right through the input signal. Also, h(n) is translated to the right, to a starting time. To view convolution in action, FIG. 3C shows h(n) shifting to the right, through x(n), one sample at a time. The values of samples coincident in time are multiplied, and overlapping time values are summed to determine the instantaneous output value. The entire sequence is obtained by moving the reversed impulse response until it has passed through the duration of the samples of interest, be it finite or infinite in length.
More generally, when two waveforms are multiplied together, their spectra are convolved, and if two spectra are multiplied, their determining waveforms are multiplied. The response to any input waveform can be determined from the impulse response of the network, and its response to any part of the input waveform. As noted, the convolution of two signals in the time domain corresponds to multiplication of their Fourier transforms in the frequency domain (as well as the dual correspondence). The bottom line is that any output signal can be considered to be a sum of impulses.
Complex Numbers
Analog and digital networks share a common mathematical basis. Fundamentally, whether the discussion is one of resistors, capacitors, and inductors, or scaling, delay, and addition (all linear, time-invariant elements), processors can be understood through complex numbers. A complex number z is any number that can be written in the form
z = x + jy
where x and y are real numbers, and where x is the real part, and jy is the imaginary part of the complex number. An imaginary number is any real number multiplied by j, where j is the square root of -1. There is no number that when multiplied by itself gives a negative number, but mathematicians cleverly invented the concept of an imaginary number. (Mathematicians refer to it as i, but engineers use j, because i denotes current.) The form x + jy is the rectangular form of a complex number, and represents the two-dimensional aspects of numbers. For example, the real part can denote distance, and the imaginary part can denote direction. A vector can be constructed, showing the indicated location.
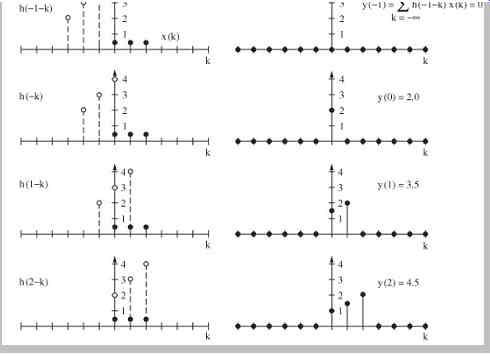
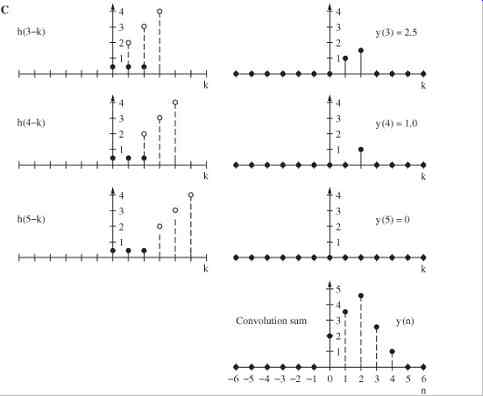
FIG. 3 A graphical representation of convolution, showing signal x(n) convolved
with h(n). A. An input signal x(n) and the impulse response h(n) of a linear
time invariant system. B. The impulse response is folded and translated.
C. The convolution sum yields the output signal y(n).
A waveform can be described by a complex number.
This is often expressed in polar form, with two parameters:
r and . The form rej
also can be used. If a dot is placed on a circle and rotated, perhaps representing a waveform changing over time, the dot's location can be expressed by a complex number. A location of 45° would be expressed as 0.707 + 0.707j. A location of 90° would be 0 + 1j, 135° would be -0.707 + 0.707j, and 180° would be -1 + 0j. The size of the circle could be used to indicate the magnitude of the number.
The j operator can be used to convert between imaginary and real numbers. A real number multiplied by an imaginary number becomes complex, and an imaginary number multiplied by an imaginary number becomes real.
Multiplication by a complex number is analogous to phase shifting; for example, multiplication by j represents a 90° phase shift, and multiplication by 0.707 + 0.707j represents a 45° phase shift. In the digital domain, phase shift is performed by time delay. A digital network composed of delays can be analyzed by changing each delay to a phase shift. For example, a delay of 10° corresponds to the complex number 0.984 - 0.174j. If the input signal is multiplied by this complex number, the output result would be a signal of the same magnitude, but delayed by 10°.
Mathematical Transforms
Signal processing, either analog or digital, can be considered in either of two domains. Together, they offer two perspectives on a unified theory. For analog signals, the domains are time and frequency. For sampled signals, they are discrete time and discrete frequency. A transform is a mathematical tool used to move between the time and frequency domains. Continuous transforms are used with signals continuous in time and frequency; series transforms are applied to continuous time and discrete frequency signals; and discrete transforms are applied to discrete time and frequency signals.
The analog relationships between a continuous signal, its Fourier transform, and Laplace transform are shown in FIG. 4A. The discrete-time relationships between a discrete signal, its discrete Fourier transform, and z transform are shown in FIG. 4B. The Laplace transform is used to analyze continuous time and frequency signals. It maps a time-domain function x(t) into a frequency domain, complex frequency function X(s). The Laplace transform takes the form:
The inverse Laplace transform performs the reverse mapping. Laplace transforms are useful for analog design.
The Fourier transform is a special kind of Laplace transform. It maps a time-domain function x(t) into a frequency-domain function X(j), where X(j) describes the spectrum (frequency response) of the signal x(t). The Fourier transform takes the form:
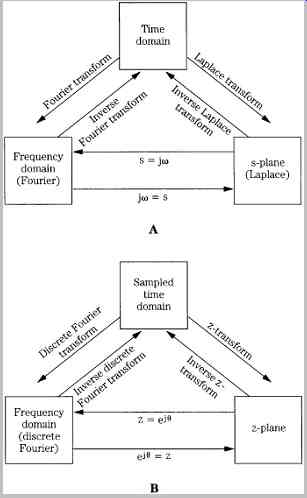
FIG. 4 Transforms are used to mathematically convert a signal from one domain
to another. A. Analog signals can be expressed in the time, frequency and s-plane
domains. B. Discrete signals can be expressed in the sampled-time, frequency,
and z-plane domains.
This equation (and the inverse Fourier transform), are identical to the Laplace transforms when s = j; the Laplace transform equals the Fourier transform when the real part of s is zero. The Fourier series is a special case of the Fourier transform and results when a signal contains only discrete frequencies, and the signal is periodic in the time domain.
FIG. 5 shows how transforms are used.
Specifically, two methods can be used to compute an output signal: convolution in the time domain, and multiplication in the frequency domain. Although convolution is conceptually concise, in practice, the second method using transforms and multiplication in the frequency domain is usually preferable. Transforms also are invaluable in analyzing a signal, to determine its spectral characteristics.
In either case, the effect of filtering a discrete signal can be predictably known.
The Fourier transform for discrete signals generates a continuous spectrum but is difficult to compute. Thus, a sampled spectrum for discrete time signals of finite duration is implemented as the discrete Fourier transform (DFT). Just as the Fourier transform generates the spectrum of a continuous signal, the DFT generates the spectrum of a discrete signal, expressed as a set of harmonically related sinusoids with unique amplitude and phase. The DFT takes samples of a waveform and operates on them as if they were an infinitely long waveform composed of sinusoids, harmonically related to a fundamental frequency corresponding to the original sample period. An inverse DFT can recover the original sampled signal. The DFT can also be viewed as sampling the Fourier transform of a signal at N evenly spaced frequency points.
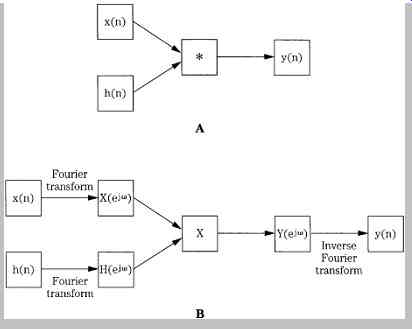
FIG. 5 Given an input signal x(n) and impulse response h(n), the output signal
y(n) can be calculated through direct convolution or through Fourier transformation,
multiplication, and inverse Fourier transformation. In practice, the latter
method is often an easier calculation. A. Direct convolution. B. Fourier transformation,
multiplication, and inverse Fourier transformation.
The DFT is the Fourier transform of a sampled signal.
When a finite number of samples (N) are considered, the N-point DFT transform is expressed as:
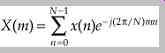
The X(m) term is often called bin m, and describes the amplitude of the frequencies in signal x(n), computed at N equally spaced frequencies. The m = 0, or bin 0 term describes the dc content of the signal, and all other frequencies are harmonically related to the fundamental frequency corresponding to m = 1, or bin 1. Bin numbers thus specify the harmonics that comprise the signal, and the amplitude in each bin describes the power spectrum (square of the amplitude). The DFT thus describes all the frequencies contained in signal x(n). There are identical positive and negative frequencies; usually only the positive half is shown, and multiplied by 2 to obtain the actual amplitudes.
An example of DFT operations is shown in FIG. 6.
The input signal to be analyzed is a simple periodic function x(n) = cos(2 n/6). The function is periodic over six samples because x(n) = x(n + 6). Three N-point DFTs are used, with N = 6, 12, and 16. In the first two cases, N is equal to 6 or is an integer multiple of 6; a larger N yields greater spectral resolution. In the third case, N = 16, the discrete spectrum positions cannot exactly represent the input signal; spectral leakage occurs in all bins. In all cases, the spectrum is symmetrical.
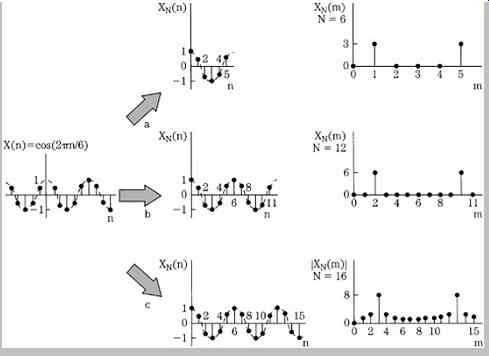
FIG. 6 Example of a periodic signal applied to an N point DFT for three different
values of N. Greater spectral resolution is obtained as N is increased. When
N is not equal to an integral number of waveform periods, spectral leakage
occurs.
The DFT is computation-intensive, requiring N2 complex multiplications and N(N - 1) complex additions. The DFT is often generated with the fast Fourier transform (FFT), a collection of fast and efficient algorithms for spectral computation that takes advantage of computational symmetries and redundancies in the DFT. The FFT requires Nlog2N computations, 100 times fewer than DFT.
The FFT can be used when N is an integral power of 2; zero samples can be padded to satisfy this requirement.
The FFT can also be applied to a sequence length that is a product of smaller integer factors. The FFT is not another type of transformation, but rather an efficient method of calculating the DFT. The FFT recursively decomposes an N-point DFT into smaller DFTs. This number of short-length DFTs are calculated, then the results are combined. The FFT can be applied to various calculation methods and strategies, including the analysis of signals and filter design.
The FFT will transform a time series, such as the impulse response of a network, into the real and imaginary parts of the impulse response in the frequency domain. In this way, the magnitude and phase of the network's transfer function can be obtained. An inverse FFT can produce a time-domain signal. FFT filtering is accomplished through multiplication of spectra. The impulse response of the filter is transformed to the frequency domain. Real and imaginary arrays, obtained by FFT transformation of overlapping segments of the signal, are multiplied by filter arrays, and an inverse FFT produces a filtered signal.
Because the FFT can be efficiently computed, it can be used as an alternative to time-domain convolution if the overall number of multiplications is fewer.

TABLE 1 Equivalent properties of discrete signals in the time domain and
z-domain.
The z-transform operates on discrete signals in the same way that the Laplace transform operates on continuous signals. In the same way that the Laplace transform is a generalization of the Fourier transform, the z transform is a generalization of the DFT. Whereas the Fourier transform operates on a particular complex value e-j , the z-transform operates with any complex value. When z = ej , the z-transform is identical to the Fourier transform.
The DFT is thus a special case of the z-transform. The z transform of a sequence x(n) is defined as:
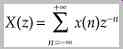
where z is a complex variable and z-1 represents a unit delay element. The z-transform has an inverse transform, often obtained through a partial fraction expansion.
Whereas the DFT is used for literal operations, the z transform is a mathematical tool used in digital signal processing theory. Several basic properties govern the z domain. A linear combination of signals in the time domain is equivalent to a linear combination in the z-domain.
Convolution in the time domain is equivalent to multiplication in the z-domain. For example, we could take the z-transform of the convolution equation, such that the z transform of an input multiplied by the z-transform of a filter's impulse response is equal to the z-transform of the filter's output. In other words, the ratio of the filter output transform to the filter input transform (that is, the transfer function H(z)) is the z-transform of the impulse response.
Furthermore, this ratio, the transfer function H(z), is a fixed function determined by the filter. In the z-domain, given an impulse input, the transfer function equals the output.
Furthermore, a shift in the time domain is equivalent to multiplication by z raised to a power of the length (in samples) of the shift. These properties are summarized in Table 17.1. For example, the z-transforms of x(n) and y(n) are X(z) and Y(z), respectively.
Unit Circle and Region of Convergence
The Fourier transform of a discrete signal corresponds to the z-transform on the unit circle in the z-plane. The equation
z = ej
defines the unit circle in the complex plane.
The evaluation of the z-transform along the unit circle yields the function's frequency response.
The variable z is complex, and X(z) is the function of the complex variable. The set of z in the complex plane for which the magnitude of X(z) is finite is said to be in the region of convergence. The set of z in the complex plane for which the magnitude of X(z) is infinite is said to diverge, and is outside the region of convergence. The function X(z) is defined over the entire z-plane but is only valid in the region of convergence. The complex variable s is used to describe complex frequency; this is a function of the Laplace transform. S variables lie on the complex s-plane.
The s-plane can be mapped to the z-plane; vertical lines on the s- plane map as circles in the z-plane.
Because there is a finite number of samples, practical systems must be designed within the region of convergence. The unit circle is the smallest region in the z plane that falls within the region of convergence for all finite stable sequences. Poles must be placed inside the unit circle on the z-plane for proper stability. Improper placement of the poles constitutes an instability.
Mapping from the s-plane to the z-plane is an important process. Theoretically, this function allows the designer to choose an analog transfer function and find the z-transform of that function. Unfortunately, the s-plane generally does not map into the unit circle of the z-plane. Stable analog filters, for example, do not always map into stable digital filters. This is avoided by multiplying by a transform constant, used to match analog and digital frequency response. There is also a nonlinear relationship between analog and digital break frequencies that must be accounted for. The nonlinearities are known as warping effects and the use of the constant is known as pre-warping the transfer function.
Often, a digital implementation can be derived from an existing analog representation. For example, a stable analog filter can be described by the system function H(s).
Its frequency response is found by evaluating H(s) at points on the imaginary axis of the s-plane. In the function H(s), s can be replaced by a rational function of z, which will map the imaginary axis of the s-plane onto the unit circle of the z plane. The resulting system function H(z) is evaluated along the unit circle and will take on the same values of H(s) evaluated along its imaginary axis.
Poles and Zeros
Summarizing, the transfer function H(z) of a linear, time invariant discrete-time filter is defined to be the z-transform of the impulse response h(n). The spectrum of a function is equal to the z-transform evaluated on the unit circle. The transfer function of a digital filter can be written in terms of its z-transform; this permits analysis in terms of the filter's poles and zeros. The zeros are the roots of the numerator's polynomial of the transfer function of the filter, and the poles are the denominator's roots. Mathematically, zeros make H(z) = 0, and poles make H(z) non-analytic. When the magnitude of H(z) is plotted as a function of z, poles appear at a distance above the z-plane and zeros touch the z-plane. One might imagine the flat z-plane and above it a flexible contour, the magnitude transfer function, passing through the poles and zeros, with peaks on top of poles, and valleys centered on zeros. Tracing the rising and falling of the contour around the unit circle yields the frequency response. For example, the gain of a filter at any frequency can be measured by the magnitude of the contour. The phase shift at any frequency is the angle of the complex number that represents the system's response at that frequency.
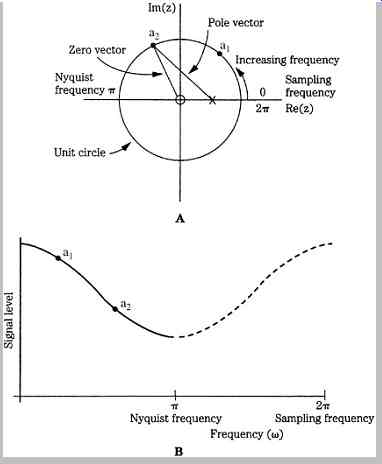
FIG. 7 The frequency response of a filter can be obtained from the pole/zero
plot. The amplitude of the frequency response (for example, at points a1 and
a2) is obtained by dividing the magnitude of the zero vector by that of the
pole vector at those points on the unit circle. A.
An example of a z-plane plot of a lowpass filter, showing the pole and zero locations. B. Analysis of the z-plane plot reveals the filter's lowpass frequency response.
If we plot |z| = 1 on the complex plane, we get the unit circle; |z| > 1 specifies all points on the complex plane that lie outside the unit circle; and |z| < 1 specifies all points inside it. The z-transform of a sequence can be represented by plotting the locations of the poles and zeros on the complex plane.
FIG. 7A shows an example of a z-plane plot.
Among other approaches, the response can be analyzed by examining the relationships between the pole and zero vectors. In the z-plane, angular frequency is represented as an angle, with a rotation of 360° corresponding to the sampling frequency. The Nyquist frequency is thus located at in the figure. The example shows a single pole ( ) and zero (o). The corresponding frequency response from 0 to the Nyquist frequency is seen to be that of a lowpass filter, as shown in FIG. 7B. The amplitude of the frequency response can be determined by dividing the magnitude of the zero vector by that of the pole vector. For example, points a1 and a2 are plotted on the unit circle, and on the frequency response graph. Similarly, the phase response is the difference between the pole vector's angle (from = 0 radians) and the zero vector's angle. As the positions of the pole and zero are varied, the response of the filter changes. For example, if the pole is moved along the negative real axis, the filter's frequency response changes to that of a highpass filter.
Some general observations: zeros are created by summing input samples, and poles are created by feedback. A filter's order equals the number of poles or zeros it exhibits, whichever is greater. A filter is stable only if all its poles are inside the unit circle of the z-plane. Zeros can lie anywhere. When all zeros lie inside the unit circle, the system is called a minimum-phase network. If all poles are inside the unit circle and all zeros are outside, and if poles and zeros are always reflections of one another in the unit circle, the system is a constant-amplitude, or all-pass network. If a system has zeros only, except for the origin, and they are reflected in pairs in the unit circle, the system is phase-linear. No real function can have more zeros than poles. When the coefficients are real, poles and zeros occur in complex conjugate pairs; their plot is symmetrical across the real z-axis. The closer its location to the unit circle, the greater the effect of each pole and zero on frequency response.
DSP Elements
Successful DSP applications require sophisticated hardware and software. However, all DSP processing can be considered in three simple processing operations:
summing, multiplication, and time delay, as shown in Fig. .8. With summing, multiple digital values are added to produce a single result. With multiplication, a gain change is accomplished by multiplying the sample value by a coefficient. With time delay (n - 1), a digital value is stored for one sample period. The delay element (realized with shift registers or memory locations) is alternatively notated as z-1 because a delay of one sampling period in the time domain corresponds to multiplication by z-1 in the z domain; thus z-1x(n) = x(n - 1). Delays can be cascaded, for example, a z-2 term describes a two-sample (n - 2) delay. Although it is usually most convenient to operate with sample numbers, the time of a delay can be obtained by taking nT, where T is the sampling interval. FIG. 9 shows two examples of simple networks and their impulse responses (see also FIG. 1B). LTD systems such as these are completely described by the impulse response.
In practice, these elemental operations are performed many times for each sample, in specific configurations depending on the desired result. In this way, algorithms can be devised to perform operations useful to audio processing such as reverberation, equalization, data reduction, limiting, and noise removal. Of course, for real time operation, all processing for each sample must be completed within one sampling period.
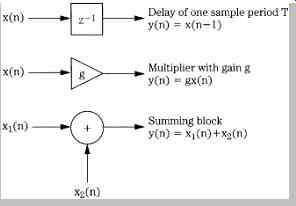
FIG. 8 The three basic elements in any DSP system are delay, multiplication,
and summation. They are combined to accomplish useful processing.
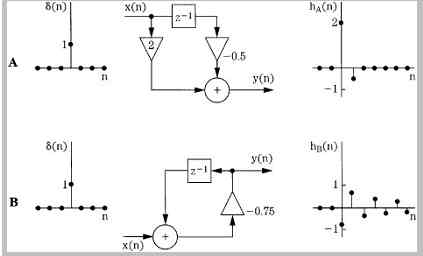
FIG. 9 LTD systems can be characterized by their impulse responses. A. A simple
nonrecursive system and its impulse response. B. A simple recursive system
and its impulse response. (Van den Enden and Verhoeckx, 1985)
Digital Filters
Filtering (or equalization) is important in many audio applications. Analog filters using both passive and active designs shape the signal's frequency response and phase, as described by linear time-invariant differential equations.
They describe the system's performance in the time domain. With digital filters, each sample is processed through a transfer function to affect a change in frequency response or phase. Operation is generally described in linear shift-invariant difference equations; they define how the discrete time signal behaves from moment to moment in the time domain. At an infinitely high sampling rate, these equations would be identical to those used to describe analog filters. Digital filters can be designed from analog filters; such impulse-invariant design is useful for lowpass filters with a cutoff frequency far below the sampling rate.
Other filter designs make use of transformations to convert characteristics of an analog filter to a digital filter. These transformations map the frequency range of the analog domain into the digital range, from 0 Hz to the Nyquist frequency.
A digital filter can be represented by a general difference equation:
y(n) + b1y(n - 1) + b2y(n - 2)+ … + bNy(n - N) = a0x(n) + a1x(n - 1) + a2x(n - 2) + … + aMx(n - M)
More efficiently, the equation can be written as:
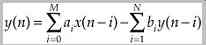
where x is the input signal, y is the output signal, the constants ai
and bi
are the filter coefficients, and n represents the current sample time, the variable in the filter's equation. A difference equation is used to represent y(n) as a function of the current input, previous inputs, and previous outputs. The filter's order is specified by the maximum time duration (in samples) used to generate the output. For example, the equation:
y(n) = x(n) - y(n - 2) + 2x(n - 2) + x(n -3) is a third-order filter.
To implement a digital filter, the z-transform is applied to the difference equation so that it becomes:
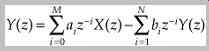
where z-i
is a unit of delay i in the time domain. Rewriting the equation, the transfer function H(z) can be determined by:
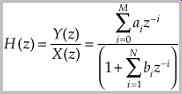
As noted, the transfer function can be used to identify the filter's poles and zeros. Specifically, the roots (values that make the expression zero) of the numerator identify zeros, and roots of the denominator identify poles. Zeros constitute feed-forward paths and poles constitute feedback paths. By tracing the contour along the unit circle, the frequency response of the filter can be determined.
A filter is canonical if it contains the minimum number of delay elements needed to achieve its output. If the values of the coefficients are changed, the filter's response is altered. A filter is stable if its impulse response approaches zero as n goes to infinity. Convolution provides the means for implementing a filter directly from the impulse response; convolving the input signal with the filter impulse response gives the filtered output. In other words, convolution acts as the difference equation, and the impulse response acts in place of the difference equation coefficients in representing the filter. The choice of using a difference equation or convolution in designing a filter depends on the filter's architecture, as well as the application.
FIR Filters
As noted, the general difference equation can be written as:
y(n) + b1y(n - 1) + b2y(n - 2) + … + bNy(n - N)
= a0x(n) + a1x(n - 1) + a2x(n - 2) + … + aMx(n - M)
Consider the general difference equation without bi terms:
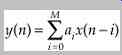
and its transfer function in the z domain:
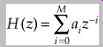
There are no poles in this equation; hence there are no feedback elements. The result is a nonrecursive filter. Such a filter would take the form:
y(n) = ax(n) + bx(n - 1) + cx(n - 2) + dx(n - 3) + …
Any filter operating on a finite number of samples is known as a finite impulse response (FIR) filter. As the name FIR implies, the impulse response has finite duration.
Furthermore, an FIR filter can have only zeros outside the origin, it can have a linear phase (symmetrical impulse response). In addition, it responds to an impulse once, and it is always stable. Because it does not use feedback, it is called a nonrecursive filter. A nonrecursive structure is always an FIR filter; however, an FIR filter does not always use a nonrecursive structure.
Consider this introduction to the workings of FIR filters:
we know that large differences between samples are indicative of high frequencies and small differences are indicative of low frequencies. A filter changes the differences between consecutive samples. The digital filter described by y(n) = 0.5[x(n) + x(n - 1)] makes the current output equal to half the current input plus half the previous input. Suppose this sequence is input: 1, 8, 6, 4, 1, 5, 3, 7; the difference between consecutive samples ranges from 2 to 7. The first two numbers enter the filter and are added and multiplied: (1 + 8)(0.5) = 4.5. The next computation is (8 + 6)(0.5) = 7.0. After the entire sequence has passed through the filter the sequence is: 4.5, 7, 5, 2.5, 3, 4, 5. The new intersample difference ranges from 0.5 to 2.5; this filter averages the current sample with the previous sample. This averaging smoothes the output signal, thus attenuating high frequencies. In other words, the circuit is a lowpass filter.
More rigorously, the filter's difference equation is:
y(n) = 0.5[x(n) + x(n - 1)]
Transformation to the z-domain yields:
Y(z) = 0.5[X(z) + z-1X(z)]
The transfer function can be written as:
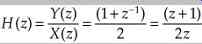
This indicates a zero at z = -1 and a pole at z = 0, as shown in FIG. 10A. Tracing the unit circle, the filter's frequency response is shown in FIG. 10B; it is a lowpass filter. Finally, the difference equation can be realized with the algorithm shown in FIG. 10C.
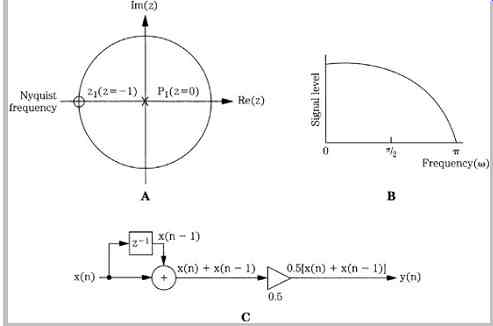
FIG. 10 An example showing the response and structure of a digital lowpass
FIR filter. A. The pole and zero locations of the filter in the z-plane. B.
The frequency response of the filter. C. Structure of the lowpass filter.
Another example of a filter is one in which the output is formed by subtracting the past input from the present, and dividing by 2. In this way, small differences between samples (low-frequency components) are attenuated and large differences (high-frequency components) are accentuated. The equation for this filter is only slightly different from the previous example:
y(n) = 0.5[x(n) - x(n - 1)]
Transformation to the z-plane yields:
Y(z) = 0.5[X(z) - z-1 X(z)]
The transfer function can be written as:
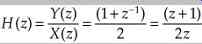
This indicates a zero at z = 1 and a pole at z = 0, as shown in FIG. 11A. Tracing the unit circle, the filter's frequency response is shown in FIG. 11B; it is a highpass filter. The difference equation can be realized with the algorithm shown in FIG. 11C. This highpass filter's realization differs from that of the previous lowpass filter's realization only in the -1 multiplier. In both of these examples, the filter must store only one previous sample value. However, a filter could be designed to store a large (but finite) number of samples for use in calculating the response.
An FIR filter can be constructed as a multi-tapped digital filter, functioning as a building block for more sophisticated designs. The direct-form structure for realizing an FIR filter is shown in FIG. 12. This structure is an implementation of the convolution sum. To achieve a given frequency response, the impulse response coefficients of an FIR filter must be calculated. Simply truncating the extreme ends of the impulse response to obtain coefficients would result in an aperture effect and Gibbs phenomenon. The response will peak just below the cutoff frequency and ripples will appear in the passband and stopband. All digital filters have a finite bandwidth; in other words, in practice the impulse response must be truncated. Although the Fourier transform of an infinite (ideal) impulse response creates a rectangular pulse, a finite (real-world) impulse response creates a function exhibiting Gibbs phenomenon. This is not ringing as in analog systems, but the mark of a finite bandwidth system.
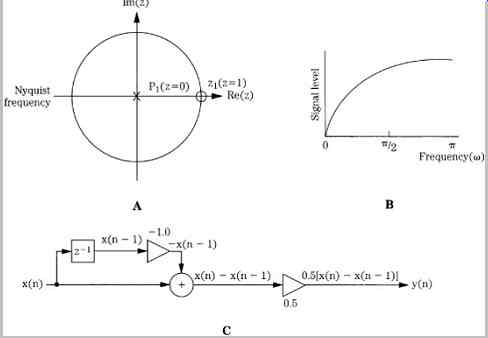
FIG. 11 An example showing the response and structure of a digital highpass
FIR filter. A. The pole and zero locations of the filter in the z-plane. B.
The frequency response of the filter. C. Structure of the highpass filter.
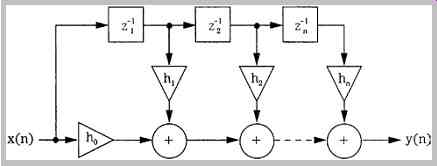
FIG. 12 The direct-form structure for realizing an FIR filter. This multi-tapped
structure implements the convolution sum.
Choice of coefficients determines the phase linearity of the resulting filter. For many audio applications, linear phase is important; the filter's constant delay versus frequency linearizes the phase response and results in a symmetrical output response. For example, the steady state response of a phase linear system to a square-wave input displays center and axial symmetry. When a system's phase response is nonlinear, the step response does not display symmetry.
The length of the impulse to be considered depends on the frequency response and filter ripple. It is important to provide a smooth transition between samples that are relevant and those that are not. In many applications, the filter coefficients are multiplied by a window function. A window can be viewed as a finite weighting sequence used to modify the infinite series of Fourier coefficients that define a given frequency response. The shape of a window affects the frequency response of the signal correspondingly by the frequency response of the window itself. As noted, multiplication in the time domain is equivalent to convolution in the frequency domain.
Multiplying a time-domain signal by a time-domain window is the same as convolving the signals in the frequency domain. The effect of a window on a signal's frequency response can be determined by examining the DFT of the window.
Many DSP applications involve operation on a finite set of samples, truncated from a larger data record; this can cause side effects. For example, as noted, the difference between the ideal and actual filter lengths yields Gibbs phenomenon overshoot at transitions in the transfer function in the frequency domain. This can be reduced by multiplying the coefficients by a window function, but this also can change the transition bands of the transfer function.
For example, a rectangular window function can be used to effectively gate the signal. The window length can only take on integer values, and the window length must be an integer multiple of the input period. The input signal must repeat itself over this integer number of samples. The method works well because the spacing of the nulls in the window transform is exactly the same as the spacing of the harmonics of the input signal. However, if the integer relationship is broken, and there is not an exact number of periods in the window, spectrum nulls do not correspond to harmonic frequencies and there is spectral leakage.
Some window functions are used to overcome spectral leakage. They are smoothly tapered to gradually reduce the amplitude of the input signal at the endpoints of the data record. They attenuate spectral leakage according to the energy of spectral content outside their main lobe.
Alternatively, the desired response can be sampled, and the discrete Fourier transform coefficients computed.
These are then related to the desired impulse response coefficients. The frequency response can be approximated, and the impulse response calculated from the inverse discrete Fourier transform. Still another approach is to derive a set of conditions for which the solution is optimal, using an algorithm providing an approximation, with minimal error, to the desired frequency response.
Also see related article: Digital Filters and DSP