Texas Instruments Code
The code to execute this five-coefficient FIR filter on a Texas Instruments TMS320xxx chip is shown below:
Of particular interest is the LTD instruction that loads a value into a register, adds the result of the last multiply to the accumulator, and shifts the value to the next higher memory address.
Line 1 moves an input data word from an I /O port to memory location XN. Line 2 zeros the accumulator. Line 3 loads the past value XNM4 into the T register. Line 4 multiplies the contents of the T register with the coefficient in H4. Lines 5 and 6 multiply XNM3 and H3, and the LTD instruction adds the result of the line 4 multiplication to the accumulator. Similarly, the other filter taps are multiplied and accumulated in lines 7 through 12. Line 13 adds the final multiplication to the accumulator, so that the accumulator contains the filtered output value corresponding to the input value from line 1. Line 14 transfers this output to YN. Line 15 transfers location YN to the I /O port. Line 16 returns the program to line 1 where the next input value is received.
When the new input is received, past values are shifted one memory location; XN moves to XNM1, XNM1 to XNM2, XNM2 to XNM3, XNM3 to XNM4, and XNM4 is dropped. Although these shifts could be performed with additional instructions, as noted, the LTD instruction (an example of the power of parallel processing) shifts each value to the next higher address after it is transferred to the T register. After line 11, the data values are ready for the next pass. Other program sections not shown would set up I /O ports, synchronize I /O with the sampling rate of external hardware, and store filter coefficients. This particular filter example uses straight-line code with separate steps for each filter tap. It is very fast for short filters, but longer filters would be more efficiently performed with looped algorithms. The decision of which is more efficient for a given filter is not always obvious.
Motorola Code
The Motorola DSP56xxx family of processors are widely used to perform DSP operations such as filtering.
Efficiency stems from the DSP chip's ability to perform multiply-accumulate operations while simultaneously loading registers for the next multiply-accumulate operation.
Further, hardware do-loops and repeat instructions allow repetition of the multiply-accumulate operation.
To illustrate programming approaches, the difference equation for the five-coefficient FIR filter in the previous example (see FIG. 19) will be realized twice, using code written by Thomas Zudock. First, as in the previous example, the filter is implemented with the restriction that each operation must be executed independently in a straight-line fashion. Second, the filter is implemented using parallel move and looping capabilities to maximize efficiency as well as minimize code size.
First, some background on the DSP56xxx family syntax and architecture. The DSP56xxx has three parallel memories, x, y, and p. Typically, the x and y memories are used to hold data, and the p memory holds the program that performs the processing. The symbols r0 and r5 are address registers. They can be used as pointers to read or write values into any of the three memories. For example, the instruction "move x:(r0) + ,x0" reads the value stored at the memory location pointed to by r0 in x memory into the x0 data register, then increments the r0 address register pointer to the data to be accessed. The x0 and y0 symbols are data registers, typically used to hold the next data that is ready for a mathematical operation. The accumulator is denoted by a; it is the destination for mathematical operations. The instruction "mac x0,y0,a" is an example of the multiply-accumulate operation; the data registers x0 and y0 are multiplied and then summed with the value held in accumulator a.
In a straight-line coded algorithm implementing the FIR example, each step is executed independently. At the start, x0 is already loaded with a new sample, r0 points to the location in x memory to save that sample, and r5 points to the location in memory where h(0) is located. The FIR straight-line code is:
In line 1, the just-acquired sample x(n), located in x0, is moved into the x memory location pointed to by r0, and r0 is advanced to point to the next memory location, the previous sample. In line 2, the filter coefficient in the y memory pointed to by r5, h(0), is read into data register y0, and r5 is incremented to point to the next filter coefficient, h(1). In line 3, x(n) and h(0) are multiplied and the result is stored in accumulator a. The initial conditions of the algorithm, and the status of the algorithm after line 3 can be described as:
Initial Status: x0 = x(n) the sample just acquired
After line 3: a = x0y0 = x(n)h(0)
The remainder of the program continues similarly, with the next data value loaded into x0 and the next filter coefficient loaded into y0 to be multiplied and added to accumulator a. After line 16, the difference equation has been fully evaluated and the filtered output sample is in accumulator a. This status can be described as:
After line 15:
a = x0y0 = x(n)h(0) + x(n - 1)h(1) + x(n - 2)h(2) + x(n - 3)h(3) + x(n - 4)h(4)
After the next input sample is acquired, the same process will be executed to generate the next output sample. Address registers r0 and r5 have wrapped around to point to the needed data and filter coefficients. The registers are set up for modulo addressing with a modulus of five (because there are five filter taps). Instead of continuing to higher memory, they wrap around in a circular fashion when incremented or decremented to repeat the process again.
Although this code evaluates the difference equation, the DSP architecture has not been used optimally; this filter can be written much more efficiently. Values stored in x and y memory can be accessed simultaneously with execution of one instruction. While values are being multiplied and accumulated, the next data value and filter coefficient can be simultaneously loaded in anticipation of the next calculation. Additionally, a hardware loop counter allows repetition of this operation, easing implementation of long difference equations. The operations needed to realize the same filter can be implemented with fewer instructions and in less time, as shown below. The FIR filter coded using parallel moves and looping is:
The parallel move and looping implementation is clearly more compact. The number of comments needed to describe each line of code is indicative of the power in each line. However, the code can be confusing because of its consolidation. As programmers become more experienced, use of parallel moves becomes familiar.
Many programmers view the DSP56xxx code as having three execution flows: the instruction execution, x memory accesses, and y memory accesses.
The Motorola DSP563xx core uses code that is compatible with the DSP56xxx family of processors. For example, the DSP56367 is a 24-bit fixed-point, 150 MIPS DSP chip. It is used to process multichannel decoding standards such as Dolby Digital and DTS. It can simultaneously perform other audio processing such as bass management, sound-field effects, equalization, and ProLogic II.
Analog Devices SHARC Code
Digital audio processing is computation-intensive, requiring processing and movement of large quantities of data. Digital signal processors are specially designed to efficiently perform the audio and communication chores.
They have a high degree of parallelism to perform simultaneous tasks (such as processing multichannel audio files), and balance performance with I /O requirements to avoid bottlenecks. In short, such processors are optimized for audio processing tasks.
The architecture used in the ADSP-2116x SHARC family of DSP chips is an example of how audio computation can be optimized in hardware. As noted, intermediate DSP calculations require higher precision than the audio signal resolution; for example, 16-bit processing is certainly inadequate for a 16-bit audio signal, unless double-precision processing is used. Errors from rounding and truncation, overflow, coefficient quantization, and limit cycles would all degrade signal quality at the D/A converter. Several aspects of the ADSP-2116x SHARC architecture are designed to preserve a large signal dynamic range. In particular, it aims to provide processing precision that will not introduce artifacts into a 20- or 24-bit audio signal.
This architecture performs native 32-bit fixed-point, 32 bit IEEE 754-1985 floating-point, and 40-bit extended precision floating-point computation, with 32-bit filter coefficients. Algorithms can be switched between fixed and floating-point modes in a single instruction cycle. This alleviates the need for double-precision mathematics and the associated computational overhead. The chip has two DSP processing elements onboard, designated PEX and PEY, each containing an arithmetic logic unit, multiplier, barrel shifter, and register file. The chip also has circular buffer support for up to 32 concurrent delay lines. To help prevent overflow in intermediate calculations, the chip has four 80-bit fixed-point accumulators; two 32-bit values can be multiplied with a 16-bit guard band. Also, multiple link ports allow data to move between multiple processors.
Dual processing units allow single-instruction multiple data (SIMD) parallel operation in which the same instruction can be executed concurrently in each processing element with different data in each element.
Code is optimized because each instruction does double duty. For example, in stereo processing, the left and right channels could be handled separately in each processing element. Alternatively, a complex block calculation such as an FFT can be evenly divided between both processing elements. The code example shown below computes the simultaneous computation of two FIR filters:
/* initialize pointers */ b0 = DELAYLINE;
I0 = @ DELAYLINE;
b8 = COEFADR;
I8 = @ COEFADR;
m1 = -2; m0=2; m8=2;
/* Circular Buffer Enable, SIMD MODE Enable */ bit set MODE1 CBUFEN I PEYEN;
nop;
f0 = dm(samples);
dm(i0,m0) = f0, f4 = pm(i8,m8);
f8 = f0* f4, f0 = dm(i0,m0), f4 = pm(i8,m8);
f12 = f0* f4, f0 = dm(i0,m0), f4 = pm(i8,m8);
Icntr = (TAPS-3), do macs until Ice;
/
* FIR loop*
/ macs: f12 = f0* f4, f8 = f8 + f12, f0 = dm(i0,m0), f4 =
pm(i8,m8);
f12 = f0* f4, f8 = f8 + f12, f0 = dm(i0,m1);
f8 = f8 + f12;
To execute two filters simultaneously in this example, audio samples are interleaved in 64-bit data memory and coefficients are interleaved in 64-bit program memory, with 32 bits for each of the processing elements in upper and lower memory. A single-cycle, multiply-accumulate, dual memory fetch instruction is used. It executes a single tap of each filter computing the running average while fetching the next sample and next coefficient.
Specialized DSP Applications
Beyond digital filtering, DSP is used in a wide variety of audio applications. For example, building on the basic operations of multiplication and delay, applications such as chorusing and phasing can be developed. Reverberation perhaps epitomizes the degree of time manipulation possible in the digital domain. It is possible to synthesize reverberation to both simulate natural acoustical environments, and create acoustical environments that could not physically exist. Digital mixing consoles embody many types of DSP processing in one consolidated control set. The power of digital signal processing also is apparent in the algorithms used to remove noise from audio signals.
Digital Delay Effects
A delay block is a simple storage unit, such as a memory location. A sample is placed in memory, stored, then recalled some time later and output. A delay unit can be described by the equation: y(n) = x(n - m) where m is the delay in samples. Generally, when the delay is small, the frequency response of the signal is altered; when the delay is longer, an echo results. Just as in filtering, a simple delay can be used to create sophisticated effects. For example, FIG. 20A shows an echo circuit using a delay block.
Delay mT is of duration m samples, and samples are multiplied by a gain coefficient (a scaling factor) less than unity. If the delay time is set between 10 ms and 50 ms, an echo results; with shorter fixed delays, a comb filter response results, as shown in FIG. 20B. Peaks and dips are equally spaced through the frequency response, from 0 Hz to the Nyquist frequency. The number of peaks depends on the delay time; the longer the delay, the greater the number of peaks.
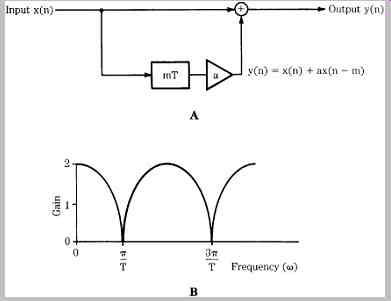
FIG. 20 A delay block can be used to create an echo circuit. A. The circuit
contains an mT delay and gain stage. B. With shorter delay times, a comb filter
response will result. (Bloom, 1985; Berkhout and Eggermont, 1985)
If the delay time of the circuit in FIG. 20A is slowly varied between 0 ms and 10 ms, the time-varying comb filter creates a flanging effect. If the time delay is varied between 10 ms and 25 ms, a doubling effect is achieved, giving the impression of an accompanying voice. A chorus effect is provided when the signal is directed through several such blocks, with different delay variations.
A comb filter can be either recursive or nonrecursive. It cascades a series of delay elements, creating a new response. Mathematically, we see that a nonrecursive comb filter, such as the one described above, can be designed by adding the input sample to the same sample delayed: y(n) = x(n) + ax(n - m) where m is the delay time in samples. A recursive comb filter creates a delay with feedback. The delayed signal is attenuated and fed back into the delay: y(n) = ax(n) + by(n - m). This yields a response as shown in FIG. 21. The number of peaks depends on the duration of the delay; the longer the delay, the greater the number of peaks.
FIG. 21 A recursive comb filter creates a delay with feedback, yielding a toothed frequency response.
An all-pass filter is one that has a flat frequency response from 0 Hz to the Nyquist frequency. However, its phase response causes different frequencies to be delayed by different amounts. An all-pass filter can be described as:
y(n) = -ax(n) + x(n - 1) + by(n - 1).
If the delay in the above circuits is replaced by a digital all-pass filter or a cascade of all-pass filters, a phasing effect is achieved: y(n) = -ax(n) + x(n - m) + by(n - m). The effect becomes more pronounced as the delay increases.
The system exhibits nonuniformly spaced notches in its frequency response, varying independently in time.
Digital Reverberation
Reflections are characterized by delay, relative loudness, and frequency response. For example, in room acoustics, delay is determined by the size of the room, and loudness and frequency response are determined by the reflectivity of the boundary surfaces and surface construction. Digital reverberation is ideally suited to manipulate these parameters of an audio signal, to create acoustical environments. Because reverberation is composed of a large number of physical sound paths, a digital reverberation circuit must similarly process many data elements.
Both reverberation and delay lines are fundamentally short-memory devices. A pure delay accepts an input signal and reproduces it later, possibly a number of times at various intervals. With reverberation, the signal is mixed repetitively with itself during storage at continually shorter intervals and decreasing amplitudes. In a delay line, the processor counts through RAM addresses sequentially, returning to the first address after the last has been reached. A write instruction is issued at each address, and the sampled input signal is routed to RAM. In this way, audio information is continually stored in RAM for a period of time until it is displaced by new information. During the time between write operations, multiple read instructions can be issued sequentially with different addresses. By adjusting the numerical differences, the delay times for the different signals can be determined.
In digital reverberation, the stored information must be read out a number of times, and multiplied by factors less than unity. The result is added together to produce the effect of superposition of reflections with decreasing intensity. The reverberation process can be represented as a feedback system with a delay unit, multiplier, and summer. The processing program in a reverberation unit corresponds to a series and parallel combination of many such feedback systems (for example, 20 or more).
Recursive configurations are often used. The single-zero unit reverberator shown in FIG. 22A generates an exponentially decreasing impulse response when the gain block is less than unity. It functions as a comb filter with peaks spaced by the reciprocal of the delay time. The echoes are spaced by the delay time, and the reverberation time can be given as: RT = 3T/log10(a) where T is the time delay and a is the coefficient. Sections can be cascaded to yield more densely spaced echoes; however, resonances and attenuations can result. Overall, it is not satisfactory as a reverberation device.
Alternatively, a reverberation section can be designed from an all-pass filter. The filter shown in FIG. 22B yields an all-pass response by adding part of the unreverberated signal to the output. Total gain through the section is unity.
In this section, frequencies that are not near a resonance and thus not strongly reverberated are not attenuated. Thus, they can be reverberated by a following section. Other types of configurations are possible; for example, Fig. .22C shows an all-pole section of a reverberation circuit which can be described as:
y(n) = -ax(n) + x(n - m) + ay(n - m).
FIG. 22 Reverberation algorithms can be constructed from recursive configurations. A. A simple reverberation circuit derived from a comb filter. B. A reverberation circuit derived from an all-pass filter. C. A reverberation circuit constructed from an all-pole section.
The spacing between the equally spaced peaks in the frequency response is determined by the delay time, and their amplitude is set by the scaling coefficients. One reverberation algorithm devised by Manfred Schroeder uses four reverberant comb filters in parallel followed by two reverberant all-pass filters in series, as shown in Fig. 23. The four comb filters, with time delays ranging from 30 ms to 45 ms, provide sustained reverberation, and the all-pass networks with shorter delay times contribute to reverberation density. The combination of section types provides a relatively smooth frequency response, and permits adjustable reverberation times. Commercial implementations are often based on similar methods, with the exact algorithm held in secrecy.
Digital Mixing Consoles
The design of a digital mixing console is quite complex.
The device is, in effect, a vast digital signal processor, requiring perhaps 109 instructions per second. Although many of the obstacles present in analog technology are absent in a digital implementation, seemingly trivial exercises in signal processing might require sophisticated digital circuits. In addition, the task of real-time computation of digital signal processing presents problems unique to digital architecture. The digital manifestation of audio components requires a rethinking of analog architectures and originality in the use of digital techniques.
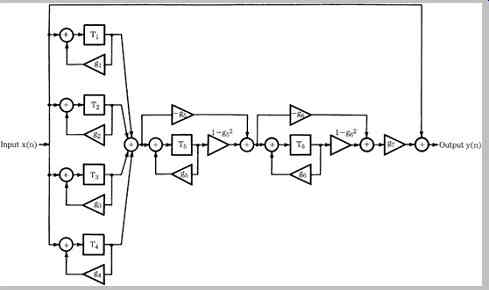
FIG. 23 Practical reverberation algorithms yielding natural sound contain
a combination of reverberation sections.
A digital console avoids numerous problems encountered by its analog counterpart, but its simple task of providing the three basic functions of attenuating, mixing, and signal selection and routing entails greater design complexity. The problem is augmented by the requirement that all operations must be interfaced to the user's analog world. A virtual mixer is much easier to design than one with potentiometers and other physical comforts. In either case, a digital console's software-defined processing promotes flexibility.
The processing tasks of a digital console follow those of any DSP system. The first fundamental task of a mixing console is gain control. In analog, this is realized with only a potentiometer. However, a digital preamplifier requires a potentiometer, an A/D converter to convert the analog position information of the variable resistor into digital form, and a multiplier to adjust the value of the digital audio data, as shown in FIG. 24A. The mixing console's second task, mixing, can be accomplished in the analog domain with several resistors and an operational amplifier. In a digital realization, this task requires a multiplexer and accumulator, as shown in FIG. 24B. The third task, signal selection and routing, is accomplished in analog with a multipole switch, but digital technology requires a demultiplexer and encoding circuit to read the desired selection, as shown in FIG. 24C. All processing steps must be accomplished on each audio sample in each channel in real time, that is, within the span of one sample period (for example, 10.4 µs at a 96-kHz sampling frequency). For real-time applications such as broadcasting and live sound, throughput latency must be kept to a minimum.
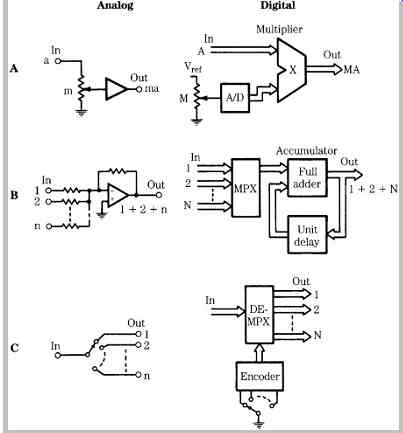
FIG. 24 The three primary functions in signal processing can be realized in
both analog and digital forms. A. Attenuating. B. Mixing. C. Selecting.
Any console must provide equalization faculties such as lowpass, highpass, and shelving filters. These can be designed using a variety of techniques, such as a cascade of biquadratic sections, a type of digital filter architecture.
The fast processing speeds and necessity for long word length place great demands on the system. On the other hand, filter coefficients are readily stored in ROM, and no more than a few thousand characteristics are typically required for most applications.
Because the physical controls of a digital console are simply remote controls for the processing circuits, no audio signal passes through the console surface. It is thus possible to offer assignable functions. Although the surface might emulate a conventional analog console with parallel controls, a set of fewer assignable controls can be used as a basic control set to view and control the mix elements.
For example, after physical controls are used to record and equalize basic tracks, they can be assigned to virtual strips that are not assigned to physical controls, then individually reassigned back to physical controls as needed. In other words, the relationship between the number of physical channel strips and the number of console inputs and outputs is flexible. The console can provide a central control section that provides access to all of the assignable functions currently requested for a particular signal path.
Particular processing functions can be assigned to a channel, inserted in the signal path, and controlled from that channel's strip or elsewhere. Physical controls on a channel strip can provide different functions, with displays that reflect the value of the selected function. A set of controls might provide equalization, or auxiliary sends. In another example, one channel strip might be assigned to a monaural, or stereo channel. As a session progresses from tracking to mix-down, the console can gradually be reconfigured, for example, adding more sends, then later creating subgroups. There is no need to limit controls to the equivalent fixed analog circuit parameters. Thus, rotary knobs, for example, might have no end stops and can be programmed for various functions or resolution. For example, equalization might be accomplished in fractions of decibels, with selected values displayed.
Console setup can be accomplished via an alphanumeric keyboard, and particular configurations can be saved in memory, or preprogrammed in presets for rapid changeover in a real-time application. Flexibility would be more of a curse than a blessing if the operator were required to build a software console from scratch each time. Therefore, using the concept of a "soft" signal path, multiple console preset configurations may be available: track laying, mix-down, return to previous setting, and a fail-safe minimum mode.
A video display might show graphical representations of console signal blocks as well as their order in the signal path. This is useful when default settings of delay, filter, equalization, dynamics, and fader are varied. In addition, each path can be named, and its fader assignment shown, as well as its mute group, solo status, phase reverse, phantom power on/off, time delay, and other parameters.
Loudspeaker Correction
Loudspeakers are far from perfect. Their nonuniform frequency response, limited dynamic range, frequency dependent directivity, and phase nonlinearity all degrade the reproduced audio signal. In addition, a listening room reinforces and cancels selected frequencies in different room locations, and contributes surface reflections, superimposing its own sonic signature on that of the audio signal. Using DSP, correction signals can be applied to the audio signal. Because the corrections are opposite to the errors in the acoustically reproduced signal, they theoretically cancel them.
Loudspeakers can be measured as they leave the assembly line, and deviations such as nonuniform frequency response and phase nonlinearity can be corrected by DSP processing. Because small variations exist from one loudspeaker to the next, the DSP program's coefficients can be optimized for each loudspeaker.
Moreover, certain loudspeaker/room problems can be addressed. For example, floor-standing loudspeakers can have predetermined relationships between the drivers, the cabinet, and the reflecting floor surface. The path-length difference between the direct and reflected sound creates a comb-filtered frequency response that can be corrected using DSP processing.
A dynamic approach can be used in an adaptive loudspeaker/room correction system, in which the loudspeakers generate audio signals to correct the unwanted signals reflected from the room. Using DSP chips and embedded software programs, low-frequency phase delay, amplitude and phase errors in the audio band, and floor reflections can all be compensated for.
Room acoustical correction starts with room analysis, performed on-site. Using a test signal, the loudspeaker/room characteristics are collected by an instrumentation microphone placed at the listening position, and processed by a program that generates room-specific coefficients. The result is a smart loudspeaker that compensates for its own deficiencies, as well as anomalies introduced according to its placement in a particular room.
Noise Removal
Digital signal processing can be used to improve the quality of previously recorded material or restore a signal to a previous state, for example, by removing noise. With DSP it is possible to characterize a noise signal and minimize its effect without affecting a music signal. For example, DSP can be used to reduce or remove noises such as clicks, pops, hum, tape hiss, and surface noise from an old recording. In addition, using methods borrowed from the field of artificial intelligence, signal lost due to tape dropouts can be synthesized with great accuracy. Typically, noise removal is divided into two tasks, detection and elimination of impulsive noise such as clicks, and background noise reduction.
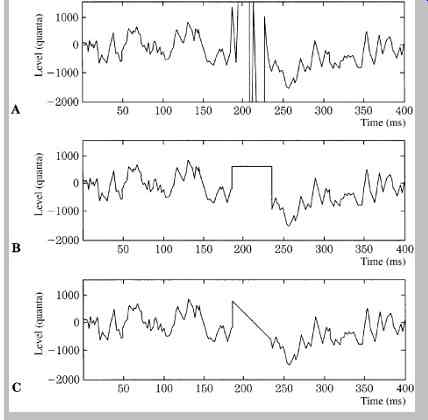
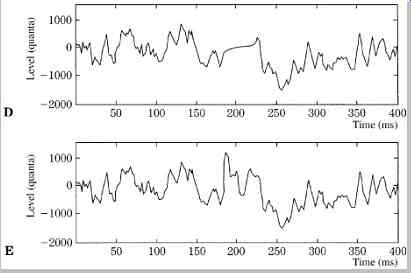
FIG. 25 Examples showing how interpolation can be used to overcome an impulsive
click. Higher-order interpolation can synthesize an essentially inaudible bridge.
A. Original sample with click. B. Sample and hold with highpass click detection.
C. Straight-line interpolation. D. Low-order interpolation. E. High-order interpolation.
Interactive graphical displays can be used to locate impulsive disturbances. A de-clicking program analyzes frequency and amplitude information around the click, and synthesizes a signal over the area of the click. Importantly, the exact duration of the performance is preserved. For example, FIG. 25 shows a music segment with a click and the success of various de-clicking methods. A basic sample-and-hold function produces a plateau that is preferable to a loud click. With linear interpolation the click is replaced by a straight line connecting valid samples.
Interpolation can be improved by using a signal model to measure local signal characteristics (a few samples).
Interpolation can be further improved by increasing the number of samples used in the model (hundreds of samples). Automatic de-clicking algorithms similarly perform interpolation over defects, but first must differentiate between unwanted clicks, and transient music information. Isolated clicks will exhibit short rise and decay times between amplitude extremes but a series of interrelated clicks can be more difficult to identify. When more than one copy of a recording is available (or when the same signal is recorded on two sides of a groove), uncorrelated errors are more easily identified. However, different recordings must be precisely time-aligned.
A background noise-removal process can begin by dividing the audio spectrum into frequency bands, then performing an analysis to determine content. The spectral composition of surface noise and hiss is determined and this fingerprint is used to develop an inverse function to remove the noise. Ideally, the fingerprint data is taken from a silent portion of the recording, perhaps during a pause.
Because there is no music signal, the noise can be more accurately analyzed. Alternatively, samples can be taken from an area of low-amplitude music, and a noise template applied.
For removal of steady-state artifacts, the audio signal is considered in small sections. The energy in each frequency band is compared to that in the noise fingerprints and the system determines what action to take in each frequency band. For example, at a particular point in the program, music can dominate in a lower spectrum and the system can pass the signal in that band unprocessed, but hiss dominating at a higher frequency might trigger processing in that band. In many cases, some original noise is retained, because the result is generally more natural sounding. In some algorithms, a clean audio signal is estimated and then analyzed to create a masking curve.
Only noise that is not masked by the curve is subjected to noise removal; this minimizes introduction of artifacts or damage to the audio signal.
Hiss from a noisy analog recording, wind noise from an outdoor recording, hum from an air conditioner, even the noise obscuring speech in a downed aircraft's flight recorder can all be reduced in a recording. In short, a processed recording can sound better than the original master recording. On the other hand, as with most technology, noise removal processing requires expertise in its application, and improper use degrades a recording.
One question is the degree to which processing is applied.
A 10 to 15% reduction in noise level can make the difference between an acceptable recording, and an unpleasantly noisy one. Additional noise removal can be problematic, even if it is only psychoacoustical tricks that make us think it is the audio signal that is being affected.
Thomas Stockham's experiments on recordings made by Enrico Caruso in 1906 resulted in releases of digitally restored material in which those acoustical recordings were analyzed and processed with a blind deconvolution method, so-called because the nature of the signals operated upon cannot be precisely defined. In this case, the effect of an unknown filter on an unknown signal was removed by observing the effect of the filtering. By averaging a large number of signals, constant signals could be identified relative to dynamic signals. In this way, the strong resonances of the horn used to make these acoustical recordings, and other mechanical noise, were estimated and removed from the recording by applying an inverse function, leaving a restored audio signal.
In essence, the acoustical recording process was viewed as a filter. The music and the impulse response of the recording system were convolved. From this analysis of the playback signal, the original performance's spectrum was multiplied by that of the recording apparatus, and then inverse Fourier transformed to yield the signal actually present on the historic recordings. Correspondingly, the undesirable effects of the recording process were removed from the true spectrum of the performance. The computation of a correction filter using FFT methods was not a trivial task. A long-term average spectrum was needed for both the recording to be restored, and for a model, higher-fidelity recording. In Stockham's work, a 1 minute selection of music required about 2500 FFTs for complete analysis. The difference between the averaged spectra of the old and new recordings was computed, and became the spectrum of the restoration filter. Restoration required multiplying segments of the recording's spectrum by the restoration spectrum and performing inverse FFTs, or by direct convolution using a filter impulse response obtained through inverse FFT.
Blind deconvolution uses techniques devised by Alan Oppenheim, known as generalized linearity or homomorphic signal processing. This class of signal processing is nonlinear, but is based upon a generalization of linear techniques. Convolved or multiplied signals are nonlinearly processed to yield additive representations, which in turn are processed with linear filters and returned via an inverse nonlinear operation to their original domain.
These and other more advanced digital-signal processing topics are discussed in detail in other texts.