|
|
Design limitations and the relative cost of PCM converter architectures encouraged the development of sigma-delta converters. These converters are characterized by short word lengths, very high oversampling rates, and noise shaping. They demonstrate that conversion can be performed either with a high-resolution quantizer at a low sampling rate (as in traditional converters), or with a low resolution quantizer at a high sampling rate (as in sigma delta converters). Sigma-delta analog-to-digital (A/D) and digital-to-analog (D/A) converters both use conversion methods such as sigma-delta modulation with noise shaping, and process high sampling-rate signals with oversampling and decimation filters. These converters share the goal of translating nonideal converter errors into uncorrelated, benign noise. Sigma-delta converters are sometimes referred to as one-bit or multi-bit converters, depending on the specific architecture employed. In addition, nonoversampling noise shaping is critical when reducing word length during a data transfer, for example, when transferring a 24-bit master recording to a 16- or 20 bit format.
Sigma-Delta Conversion
Conversion of PCM audio data words, using a resistor ladder, is a traditional approach. A PCM system represents the analog waveform as an amplitude signal, storing information that measures the amplitude sample by sample. However, the method is flawed when quantization introduces differential nonlinearity errors in the amplitude representation. Moreover, because a multiplicity of bits are used to form the representation, and because each bit has an error unequal to the others, the overall error varies with each sample, and is thus difficult to correct. In practice, calibration procedures during manufacture, and sophisticated circuit design are required to achieve high performance. Understandably, manufacturers sought to develop alternative conversion methods, including sigma delta converters. Sigma-delta methods are particularly desirable for A/D conversion because they obviate the need for an analog brick-wall anti-aliasing filter. But the method also offers many advantages in D/A conversion, particularly when designing a mixed-signal integrated circuit that combines A/D, D/A, and DSP functions.
It is not easy to see how one bit (or a few) can replace 16 or more bits. Consider this analogy: traditional ladder converters are like a row of light bulbs, each connected to a switch. Sixteen bulbs, for example, each with a different brightness, can be lighted in various combinations to achieve 216 or 65,536 different brightness levels. However, relative differences in individual bulb intensities will introduce error into the output brightness level. Any particular switch combination may not exactly produce the desired brightness. Similarly, ladder converters introduce error as they attempt to reproduce the audio signal.
Sigma-delta technology uses a wholly different approach. Instead of many bulbs and switches, only one bulb and one switch are used. Brightness is varied by simply switching the bulb on and off. For example, if the bulb is dynamically switched on and off equally, the output is at half-brightness. If the bulb's on-time is increased, brightness will increase. Similarly, sigma-delta converters may ideally use one bit to represent audio amplitude, with very fast switching and very accurate timing. Sigma-delta technology is an inherently precise way to represent an audio waveform.
PCM conversion divides the signal in multiple amplitude steps. However, sigma-delta conversion divides the signal in time, keeping amplitude changes constant. Non-intuitively, a high- or low-level pulse signal can represent an audio signal. For example, pulse-density modulation (PDM) can be used. FIG. 1 shows how a single constant-width pulse, with either a high or low level, can reconstruct a waveform. Alternatively, a pulse-width modulation (PWM) signal can be used to reconstruct the output signal (variations are pulse-edge and pulse-length modulation).
Sigma-delta converters are called one-bit converters when one quantized audio bit is output, and called multi-bit converters when the audio signal is quantized to several bits (perhaps four). True one-bit sigma-delta converters output full-scale positive or negative pulses that ensure perfect linearity. However, their inherently coarse quantization yields a higher noise floor. Thus, higher orders of noise shaping are required for good in-band dynamic range performance. In addition, one-bit converters are susceptible to phase jitter on the modulator clock.
Relatively small jitter levels can yield a full-scale error in the one-bit signal. Multi-bit sigma-delta converters use multiple quantization levels and this yields a relatively lower noise floor both in-band and out of band. This allows the use of a relatively lower oversampling ratio, as well as lower-order noise shaping. In addition, the smaller quantization levels of multi-bit converters make them more tolerant of phase jitter.
However, care must be taken to achieve good linearity.
Generally, multi-bit sigma-delta converters are employed in higher-quality audio applications.
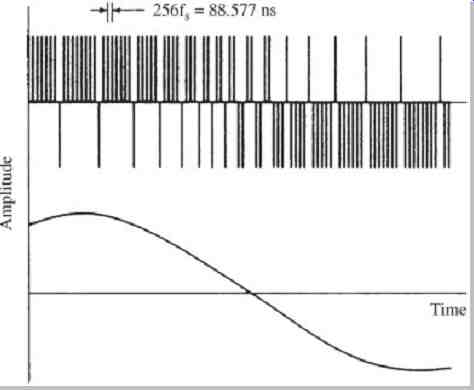
FIG. 1 Pulse-density modulation can be used to code and reconstruct an analog
waveform.
One-bit sigma-delta converters are inherently linear; any level mismatch results in an offset. However, multi-bit sigma-delta converters can have element mismatches that result in noise and distortion. In this architecture, a capacitor or resistor element is assigned to a fixed code; small variations yield a mismatch. For example, assuming 32 elements, a 1% mismatch yields about 0.1% THD + N distortion. The distortion is also signal-dependent. To address this mismatch, codes can be used to randomly assign different elements in each cycle, but this increases noise. Assuming 32 elements and an oversampling ratio of 128, a 1% mismatch would yield a dynamic range of only 80 dB. Dynamic element matching (DEM) is a common solution used to reduce the effect of mismatch errors in the conversion elements of multi-bit converters. With DEM, analog capacitor elements are swapped so that the mismatch error is averaged close to zero. DEM can use open-loop noise shaping after the modulator to convert the error into low-level benign noise. For example, elements can be selected cyclically, depending on the weighting of the input data. This averages the mismatch, and the noise from mismatching is first-order noise shaped. In other designs, the mismatch shaping function can be placed inside the sigma-delta feedback loop. The randomized errors are shaped by the modulator, further reducing the in band level. Assuming 32 elements and an oversampling ratio of 128, a 1% mismatch would yield a dynamic range of 120 dB.
Sigma-delta conversion methods are widely used in digital audio products. These techniques are extremely competitive in both A/D and D/A applications because they obviate the need for analog brick-wall filters. Although sigma-delta methods use familiar techniques such as oversampling, highly sophisticated processing is required to implement noise shaping and thus decrease the high in band noise levels otherwise present in sigma-delta conversion. A variety of sigma-delta A/D and D/A architectures have been devised, with different algorithms and orders of noise shaping.
Delta Modulation
In PCM a signal is sampled and quantized into discrete steps; the maximum signal amplitude determines the maximum quantizer range. Traditional PCM A/D and D/A converters are shown in FIG. 2A. Quantization error is uniformly present across the Nyquist frequency band from 0 to fs/2 Hz and cannot be removed from the signal; fs is the sampling frequency. If quantization is performed at a higher sampling frequency R × fs Hz where R is the oversampling rate, the error is spread across the band to R × fs/2 Hz, hence the noise in the audio band is reduced by 3 dB for every factor of 2 oversampling.
With a maximum-amplitude sinusoidal input signal, oversampling will increase the signal-to-error ratio as follows:
S/E = 6.02(N + 0.5L) + 1.76 dB
where N = the number of quantization bits
L = the number of octaves of oversampling
For example, an oversampling A/D converter can perform as well as a longer word length A/D converter, yielding a benefit of 0.5 bit/oversampling octave. However, the benefit is limited. For example, a 10-bit improvement would require an L of 20 octaves, equivalent to an impossible oversampling factor of 1 million. It is the aim of noise shaping to introduce a highpass function in the noise spectrum and thus improve oversampling performance.
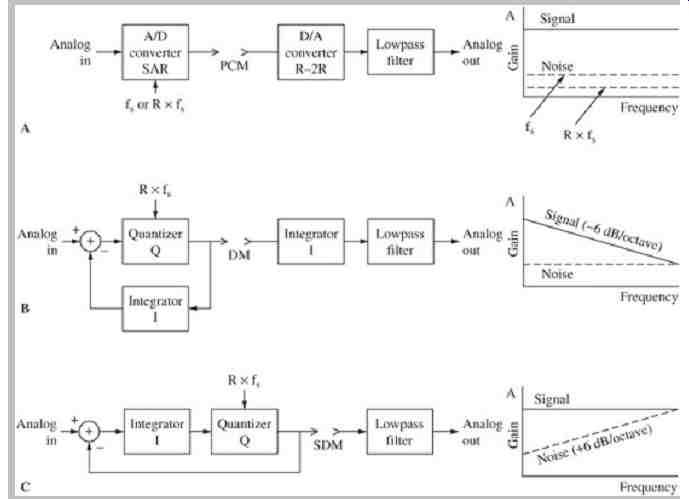 FIG. 2 A comparison of modulation methods used in A/D and D/A conversion.
A. Pulse-code modulation (PCM) yields a flat signal and noise floor. B. Delta
modulation (DM) yields a signal that falls with frequency. C. Sigma delta modulation
(SDM) yields a noise floor that rises with frequency.
FIG. 2 A comparison of modulation methods used in A/D and D/A conversion.
A. Pulse-code modulation (PCM) yields a flat signal and noise floor. B. Delta
modulation (DM) yields a signal that falls with frequency. C. Sigma delta modulation
(SDM) yields a noise floor that rises with frequency.
Delta modulation and sigma-delta modulation (also called delta-sigma) were developed in the 1940s and 1960s, respectively, for voice telephony applications.
Limitations prohibited their use in high-quality music applications until the emergence of high-speed digital signal processing techniques in the 1980s, that improved audio performance. Differential pulse-code modulation (DPCM) is a technique in which the derivative of the signal is quantized. When signal changes between sample periods are small, the quantizer's word length can be reduced. With very high oversampling rates, the changes between sample periods are made very small, thus the quantizer can be reduced to one bit. A one-bit DPCM coder is known as a delta modulator (DM). In other words, DM codes the differences in the signal amplitude, its slope, instead of the signal amplitude itself. In contrast, a sigma DPCM technique places an integrator at the input to the quantizer. Instead of coding the slope of the signal, sigma DPCM, like PCM, codes its amplitude. However, with sigma-DPCM, the signal can be quantizing to only one or a few bits; both implementations are generally known as sigma-delta modulation. As with delta modulation, sigma delta modulation requires high oversampling rates.
A delta-modulation encoder and decoder are shown in FIG. 2B; this is known as a single integration modulator.
The analog input signal is compared to the integrated output pulses and the delta (difference) signal is applied to the quantizer. The quantizer generates a positive pulse when the difference signal is negative, and a negative pulse when the difference signal is positive. This difference error signal moves the integrator step by step closer to the present value input, tracking the derivative of the analog input signal. The integrator's output is a past approximation to the input, thus the coder operates similarly to other integrating feedback loops such as phase-locked loops.
A delta-modulation decoder consists of an integrator and a lowpass filter. When the one-bit pulses are integrated using a time constant that is long compared to the sample period, a step waveform is produced. An output analog waveform is produced by low-pass filtering this step waveform. Requantization error at the output of the integrator is white. As in PCM, oversampling decreases the error level by 3 dB for every factor of two oversampling.
The dynamic range can be improved, that is, the requantization error made smaller, by making the delta (difference or step size) value smaller. The limit to which the delta can be reduced is given by the maximum derivative of the signal. The coded signal amplitude decreases at 6 dB/octave; thus, S/N decreases as the signal frequency increases.
The maximum derivative occurs at maximum signal frequency and maximum signal amplitude. Exceeding this limit causes slope overload distortion. For music signals, the delta value must be high, resulting in a high quantization error level. When the signal has reduced high-frequency content, as in speech, delta can be reduced. In any case, the success of DM hinges on assumptions about the nature of the encoded signal. This dependence of the dynamic range on the signal spectrum, and good performance only when the signal has lowpass characteristics, as well as correlated patterns at low signal levels, limits single integration DM applications.
To convert a maximum amplitude 16-bit word, a one-bit modulator would have to perform 216 toggles per conversion period. With a sampling frequency of 44.1 kHz, this would demand an unrealistic toggle rate of approximately 2.9 GHz. As the rate is slowed to accommodate hardware limitations, noise levels increase to an intolerable level. Looked at in another way, bit reduction at a high sampling frequency is required to output a one-bit signal from a high-bit source; this greatly degrades the signal's dynamic range.
Sigma-Delta Modulation
Sigma-delta modulation (SDM) was developed to overcome the limitations of delta modulation. Sigma-delta systems quantize the delta (difference) between the current signal and the sigma (sum) of the previous difference. A first-order (single integration) sigma-delta modulation encoder and decoder are shown in FIG. 2C. An integrator is placed at the input to the quantizer; signal amplitude is constant with increasing frequency. The input to the midrise quantizer is the integral of the difference between the input and the quantized output as applied via negative feedback. If the input signal in one sample period is greater than the value accumulated in the feedback loop over previous samples, the converter outputs a "1." Otherwise, if it is lower, the output is a "0." In other words, the difference between the input signal and the accumulated error is quantized. When the error is sufficiently large, the quantizer changes state to reduce the error. Thus, the difference between the input signal and the output signal approaches zero; the average value of the output approximates the input. There is little dc error in the output signal. However, the frequency spectrum of the quantizing error rises with increasing frequency (6 dB/octave).
The integrator forms a lowpass filter on the difference signal thus providing low-frequency feedback around the quantizer. This feedback results in a reduction of quantization noise at low (in-band) frequencies. Unlike PCM and DM, the noise floor is not flat, but shaped by a first-order highpass characteristic as analyzed below. In practice, the in-band noise floor level is not satisfactory with first-order sigma-delta modulation. In addition, quantization noise is highly correlated in a first-order modulator. Further noise shaping must be achieved with higher-order (multiple integration) sigma-delta modulation coders. Michael Gerzon and Peter Craven have shown that shaped noise in multi-bit noise shapers will occupy equal areas above and below the original noise level. Since this relationship occurs on a logarithmic vertical axis and linear frequency axis, shaping increases the total noise power. The benefit, of course, is lower in-band noise.
Like PCM, sigma-delta modulation quantizes the signal amplitude directly, and not its derivative as in DM. Thus the maximum quantizer range is determined by the maximum signal amplitude and is not dependent on signal spectrum.
As with delta modulation, to achieve high resolution, high oversampling rates are required. For example, with an audio band of 24 kHz and 64 times oversampling, the internal sampling frequency rises to 3.072 MHz, thus quantization noise is spread from dc to 1.536 MHz..
However, because the quantizer has only two states, the quantization error, and the resulting noise level, is high. To overcome this, sigma-delta modulators add noise shaping to move the noise power to higher, out-of-band frequencies. The noise is shaped by the inverse of the loop transfer function; when a lowpass filter is placed in the loop, the noise spectrum increases with frequency. In many designs, a multi-bit quantizer is used within the loop and a low-bit PCM signal is coded; the dynamic range increases with 6 dB for every quantization bit. As in one-bit designs, the noise floor increases by 6 dB/octave in multi-bit designs, and noise shaping is required.
A one-bit sigma-delta modulation decoder theoretically requires only a lowpass filter to decode the signal, to remove high-frequency (out-of-band) components. In other words, it averages the output signal to produce an analog waveform. An integrator is not needed in the decoder (as in DM) because the signal's amplitude is coded, not its slope.
In multi-bit designs, a D/A converter is needed in the decoder to decode the low-bit PCM signal.
Analysis of a First-Order Sigma-Delta Modulator
The signal and noise transfer functions for a first-order sigma-delta modulator are analyzed in FIG. 3. X(z) is the z-transform of the input sequence and Y(z) represents the output sequence. The quantization error is represented as white noise N(z). For a zero noise source, the transfer function shows a lowpass characteristic. For a zero signal, the transfer function shows a highpass characteristic. In other words, as the loop integrates the difference between the input signal and the sampled signal, it lowpass filters the signal and highpass filters the noise. If the system is designed so the signal's frequency content is less than the filter's cutoff frequency, the signal will not be affected. Given a first-order noise-shaping loop, with a maximum amplitude sinusoidal input, the maximum signal-to-error ratio will be:
S/E = 6.02(N + 1.5L) -3.41 dB
where N = the number of quantization bits
L = the number of octaves of oversampling
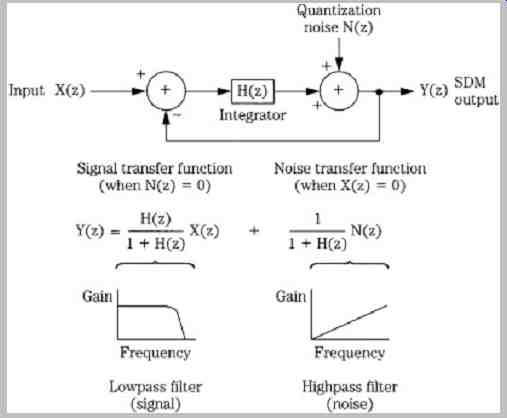
FIG. 3 A z-transform analysis of a sigma-delta modulator. (Hauser, 1991)
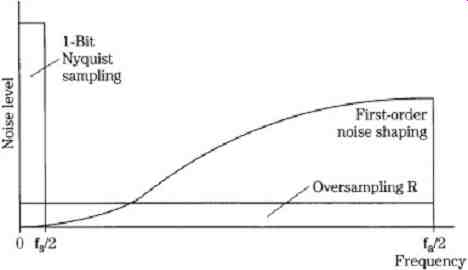
FIG. 4 With one-bit conversion, quantization noise is quite high. In-band
noise is reduced with oversampling.
With noise shaping, quantization noise is shifted away from the audio band, further reducing in-band noise.
For example, an A/D converter with sigma-delta first order noise shaping provides a benefit of 1.5 bits/octave compared to an oversampling converter without a noise shaping loop.
The performance of a sigma-delta converter relies on both oversampling, and its noise-shaping characteristic.
The quantization noise floor falls from 0 to fs/2 Hz and is quite high, as shown in FIG. 4. Quantization noise is reduced with an R oversampling ratio because noise is spread over a 0-Hz to fa/2-Hz spectrum where fa = R × fs Hz. With sigma-delta noise shaping, in-band noise (0 to fs/2) is further decreased and out-of-band noise is increased.
FIG. 5 summarizes the mathematical basis of first order sigma-delta noise shaping. Quantization noise is assumed to be random, and the quantizer is modeled as an additive noise source. Note that the (1 - z-1) factor doubles quantized noise power; however, the same factor also shifts the noise to higher frequencies. This sigma-delta modulator forms the basis for many A/D and D/A one-bit and multi-bit converters.
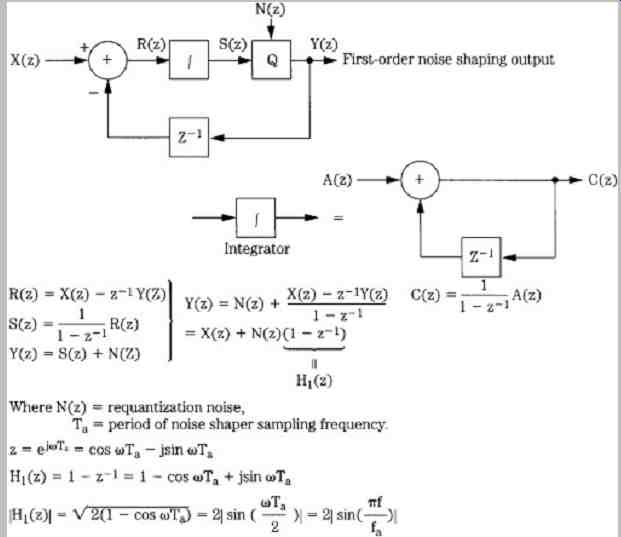
FIG. 5 Analysis of a first-order sigma-delta noise shaper.
Higher-Order Noise Shaping
As noted, first-order (single integration) sigma-delta modulation is not satisfactory for high-fidelity audio performance. Higher-order loops further decrease in-band quantization noise, with the penalty of increased total noise power. For example, a second-order loop would yield:
S/E = 6.02(N + 2.5L) - 11.14 dB
This provides a benefit of 2.5 bits/octave, with a fixed noise penalty approximately equal to two equivalent bits.
The input/output characteristic of a basic sigma-delta noise shaper of nth order is:
Y(z) = X(z) + (1 - z1) / n N(z)
where Y(z) = the noise-shaped output
X(z) = the input signal
n = the order of the differentiation
N(z) = the quantization noise (assumed to be white)
This characteristic can be theoretically composed of n cascaded digital differentiators. As n increases, the slope in frequency of the shaping function increases, thus it is more effective in suppressing low-frequency noise.
However, the out-of-band noise could overly burden subsequent analog filters. A successful noise-shaping circuit thus seeks to balance a high oversampling rate with noise-shaping order to reduce in-band noise and shift it away from the audible range. Higher-order noise-shaping loops can remove even more in-band noise overall, but relatively more noise is present near the Nyquist frequency.
Hence these algorithms are more effective at high oversampling rates so there is more spectral space between the highest audio frequency and the Nyquist frequency; this allows the use of very simple analog lowpass filters.
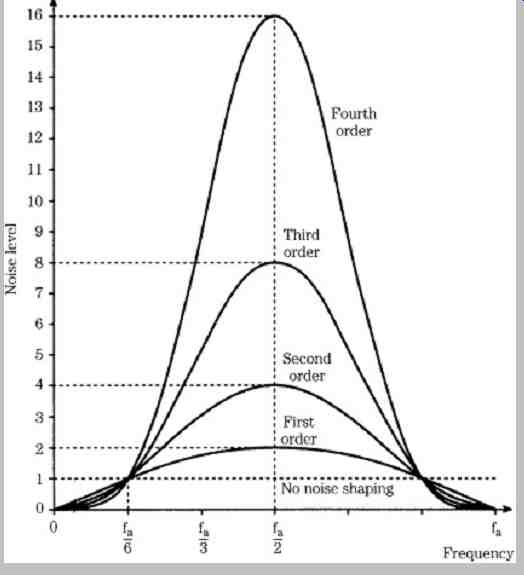
FIG. 6 Higher orders of noise shaping result in more pronounced shifts in
requantization noise.
Using first-order and higher-order noise-shaping algorithms, a series of noise-shaping curves can be generated, as shown in FIG. 6. As higher orders of noise shaping are used, the in-band noise level is decreased.
The frequency response curves described by sigma-delta noise-shaping equal a unity value at fa/6 Hz where fa is the noise-shaping oversampling frequency. Noise is reduced only for f < fa/6 Hz, and increased for fa/6 < f < fa/2 Hz. The noise level reaches a maximum at fa/2 Hz. As the oversampling rate is increased, the portion of the noise curve in the audio band is relatively reduced. Although the shape of the noise curve remains the same, high oversampling rates relatively decrease in-band noise.
In a traditional noise-shaper design, the poles of the loop filter are at 0 Hz, as in an ideal integrator; this results in zeros in the audio band. In some noise-shaper designs, a technique called zero-shifting is used to modify the rising noise spectrum by shifting one or more zeros to the edge of the audio band (for example, 18 kHz). For example, when two zeros are shifted in a third-order noise filter, noise in the range from 13 kHz to 20 kHz can be reduced, but increased below 13 kHz. Overall, the noise measurement is enhanced. However, suppression of idle patterns and thresholding effects can be diminished; thus, the zero shifting technique must be used with care.
Idle Tones and Limit Cycles
The low-level linearity of low-order (particularly first-order) sigma-delta noise-shaping algorithms can be degraded by idle tones. The quantization noise is not always random, and instead can be correlated to the input signal. This is an idle tone, a high-frequency oscillation of the modulator output. Given a zero input signal, a noise shaper can output an alternating 1010 pattern. A very low-level input might result in a similar 1010 pattern, but disturbed by double 1s and 0s. If the period of the repetition of such patterns is long enough, they yield energy that might fall in the audio baseband, being audible as a deterministic or oscillatory tone, rather than as noise. Because they occur when the channel is idling, these nonlinear patterns are called idle tones, or idling patterns, and result in idle channel noise.
The double codes will be generated, or not, depending on the duration of the input signal. The phenomenon is especially characteristic of low-amplitude, high-frequency sine waves. Because the phenomenon has a frequency dependent threshold level, below which the signal is not coded, the effect is sometimes called thresholding.
First-order sigma-delta noise shapers particularly exhibit these effects because of their stable 1010 patterns. Higher order noise shapers are much less prone to the problem because their output patterns are less stable. Thus, for example, virtually all sigma-delta converters use at least a second-order modulator loop. However, in many multistage designs, the effect can occur in each of the cascaded low order stages. Thus, it is important to add a dither signal in the first stage to disturb any fixed patterns and remove the correlation. Dither is applied most effectively in multi-bit converters, and less effectively in true one-bit converters.
Generally, multi-bit converters are completely linearized with triangular pdf dither, which eliminates noise modulation but slightly increases the level of the noise floor. It is felt that true one-bit converters cannot be fully dithered because this would overload the modulator. In true one-bit converters, dither has both advantages and disadvantages and the optimum dithering technique has not yet been found; other methods are sometimes used to linearize the converter.
A limit cycle is a repeating output sequence. It will yield spurious spectral lines and potentially audible distortion on the output. Limit cycles may occur even in simple noise shapers for some input signals such as a dc input. Their occurrence also depends on the initial state of the noise shaper filter. Limit cycles can generally be avoided by adding sufficient dither. For example, high-order noise shapers can use small dither levels, such as a rectangular pdf dither with a peak-to-peak amplitude of 0.01 LSB.
Higher-order sigma-delta modulation loops offer wider dynamic range and overall better performance, but loops greater than second-order can be unstable. The quantizer is nonlinear because its effective "gain" inversely varies with the input level. A large input signal can overload the loop, reducing the gain of the quantizer, thus causing instability that will persist even after the signal is withdrawn.
For example, a powering-up transient could cause a converter to oscillate. Converters thus sense instability by counting the number of consecutive ones or zeroes in the bitstream, and reset when necessary.
One-Bit D/A Conversion with Second-Order Noise Shaping
A sigma-delta D/A converter comprises a digital interpolation filter, sigma-delta modulator, one-bit or multi bit converter, and a low-order lowpass output filter. The input digital word, with long word length, is applied to the interpolation filter that lowpass filters the signal and increases its sampling rate with oversampling. The digital modulator noise-shapes the signal and reduces the word length to one or a few bits. For example, its transfer function can be implemented with an I IR filter. The signal is effectively lowpass-filtered and the quantization noise is highpass-filtered. The analog output filter removes the high frequency shaped quantization noise as well as high frequency images.
One implementation of a true one-bit D/A conversion method comprises an over-sampling filter, second-order sigma-delta noise shaping, and pulse-density modulation (PDM) output. The sampling frequency is increased from 44.1 kHz to 11.2896 MHz, an increase of 256 times. At the same time, the 16-bit signal is converted to a one-bit signal that reconstructs the audio waveform. The requantization error of the output signal is corrected by feedback. Instead of outputting a signal with conventional quantization error, the error undergoes sigma-delta processing to attenuate its in-band level.
The output bit, operating at a frequency of 11.2896 MHz, is converted to an analog signal using a simple switched capacitor network. Specifically, a capacitor is charged and discharged according to the 1 or 0 value of the data. The result is an analog waveform that reflects the encoded waveform through time-averaging of the output bit. The network's operation is accurate, and hence the error of the signal is low. There are only positive and negative full-scale reference points. Errors in the reference values will generate a gain offset error, but not a linearity error. The offset error can easily be removed. In practice, nonlinearities could result from idle patterns in the noise shaping circuitry.
FIG. 7 represents the operation of a one-bit PDM converter. It performs noise shaping through feedback loops and generates a one-bit signal for conversion to analog. The noise shaper consists of two integration (filter) loops to reduce in-band requantization noise. The output (H) of the quantizer is +1 if its input is positive (MSB = 0), and -1 if its input is negative (MSB = 1); the one-bit code output from the quantizer is simply a sign bit. Following a limiting operation designed to prevent overflow, the remainder of each sample is fed back as a quantization error. The error signal (I) is fed back into the double integration loops. Values inside the loop exceed the unit value; in other words, wider data buses are required. In this case, a 21-bit data bus is used within the loop; signals are processed in two's complement form.
Also, if large values are input to the circuit, the limiter would be needed to prevent overloading of the loops.
Ideally, with no input signal, the coder should output only a tone at R × fs/2 Hz where R is the oversampling rate.
However, idle tones can also occur at additional frequencies. To overcome this, dither can be added to the input data so the circuit always operates with a changing signal even when the audio signal is zero or dc.
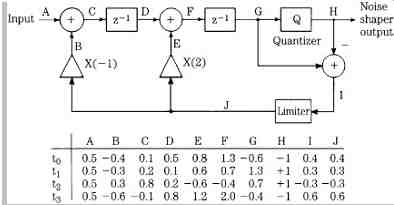
FIG. 7 Operation of a second-order noise-shaping circuit.
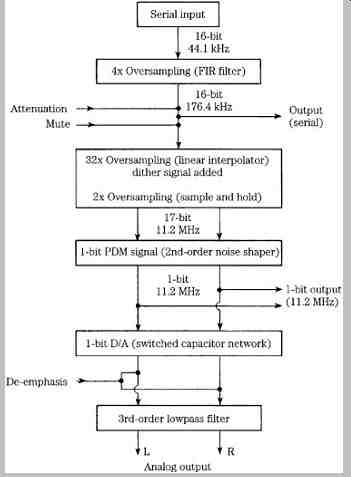
FIG. 8 Processing elements in a second-order, pulse density modulation D/A
conversion system.
FIG. 8 shows the complete system, including the one-bit PDM noise-shaper modeled above. The first of the three oversampling stages performs four-times over sampling to attenuate image spectra; in addition, first-order noise shaping is performed in the filter. The second stage performs 32-times oversampling. A dither signal (-20 dB at 352 kHz) is added to prevent idle tones from causing nonlinearity. Two-times oversampling is performed in the third stage. This 17-bit signal (dither adds one bit to the original 16-bit signal) undergoes second-order noise shaping as described above, and a single bit is output from the quantizer. Finally, D/A conversion is accomplished at a one-bit D/A converter via pulse-density modulation that outputs two-valued (±) data at 256-times oversampling, or 11.2896 MHz. A third-order analog lowpass filter removes out-of-band high-frequency components.
The output signal conveys the audio waveform through the density of pulses above and below zero (see FIG. 1); this pulse-density modulation signal is converted to an analog signal using a switched dual-capacitor network.
Two control signals representing the data stream's logic 0 and logic 1 values control the switching of the capacitors, subject to a clock pulse. During the negative half of the clock, the first capacitor discharges while the second capacitor charges. During the positive half, if the data is 1, the first capacitor is charged by taking a fixed amount of charge from the summing node of an operational amplifier.
If the data is 0, a fixed charge is transferred into the summing node from the second capacitor. In this way, there are only positive and negative full-scale reference points, and intermediate points are determined by time averaging.
There is no MSB change around zero, for example, because zero is represented by an equal number of positive and negative full-scale pulses. Zero-cross distortion is thus eliminated.
In this one-bit converter, the quantization noise introduced by the word length reduction is spectrally shaped by a lowpass feedback loop around the quantizer (see FIG. 7). Second-order noise shaping is performed:
where Y(z) = the noise-shaped output
X(z) = the input signal
N(z) = the quantization noise
The requantization noise of the output signal is corrected by feedback, and noise shaping attenuates its in-band level. As a result, the spectrum of the noise in the output signal is shifted away from the audio band. FIG. 9 summarizes the mathematical basis of second-order noise shaping.
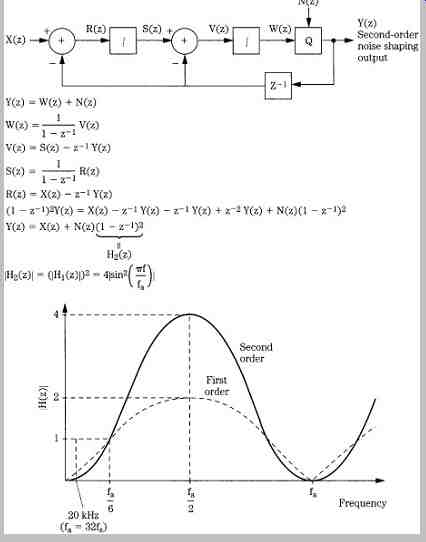
FIG. 9 Analysis of a second-order noise shaper.
Multi-Bit D/A Conversion with Third-Order Noise Shaping
When the noise-shaping circuits in sigma-delta modulators exceed second order, the noise-shaping feedback loops can pose overload or oscillation problems. For example, an overload would effectively reduce the magnitude of loop gain, lowering the crossover frequency, where phase shift is too large for stability. When a loop filter H(z) has three or more integrations, its phase shift can be 180° at the frequency where the loop gain magnitude reaches unity at the crossover frequency.
Higher-order noise shapers overcome this problem with a more complex loop architecture that often uses multistage noise shaping. The loop filter H(z) provides a high-order lowpass response at low baseband frequencies, but gain drops to a first- or second-order lowpass response nearer the crossover frequency. This approach provides good in-band noise shaping, with sufficient conditional stability.
The MASH system is a multistage third-order noise shaping method. It is an example of a practical multi-bit converter. One implementation of this design accepts 16 bit words at a nominal sampling frequency, and a digital filter performs eight-times oversampling and outputs 24-bit words. Noise-shaping circuits output 11-valued data, at a 32-times oversampling rate. D/A conversion is accomplished via pulse-width modulation (PWM), outputting the data at a 768-times oversampling rate.
As noted, generally, if noise-shaping circuits exceed second-order they can be prone to oscillation from instability. To avoid such errors, this third-order implementation uses a multistage configuration. A simplified schematic for the complete noise shaper is shown in FIG. 10; it contains a first-order noise shaper in parallel with a second-order noise shaper. The input signal is applied to quantizer Q1 after the error signal through the delay block is subtracted from the input. The signal output from the first loop is also applied to the second loop. The output of quantizer Q2 is differentiated and added to the output of the first loop to form the final output signal. Thus, the requantization error of the first loop is requantized by the second, and canceled by adding the requantized noise to the first loop's signal. The outputs of each stage can be characterized as:
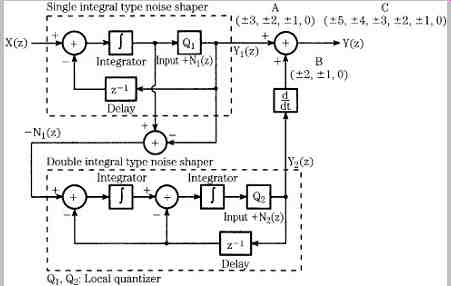
FIG. 10 A multistage third-order noise-shaping circuit with output of 11
data values before PWM reconstruction.
...where Y1(z) and Y2(z) = the outputs of stages 1 and 2, respectively
X(z) = the input signal
N1(z) and N2(z) = quantization noise of the local quantizers Q1 and Q2, respectively
When both sides of the second equation are multiplied by (1 - z-1) and this is added to the first equation, observe that the quantization error of the first stage can be canceled. By passing the output of the second stage through a differentiator and adding it to the output of the first stage, the overall circuit output is:
In other words, the quantization error N2(z) is output with a third-order differential characteristic (18 dB/octave), achieving reduced in-band noise compared to first- and second-order characteristics.
Input data is linearly requantized into a multi-bit output digital signal with seven values (±3, ±2, ±1, 0) at the main loop, and at the sub-loop the requantization error is requantized into five values (±2, ±1, 0). When these output values are added together, the digital signal output from the circuit represents 11 values (± 5, ± 4, ± 3, ± 2, ±1, 0).
These different data values are shown graphically in Fig. 11. Using a vertical scale to represent amplitude of the values, it can be seen that the main loop outputs seven values of rough accuracy, and the sub-loop outputs five values with high-frequency content, used to eliminate the requantization error of the main loop. When summed, 11 values are output from the shaper to reconstruct the audio signal.
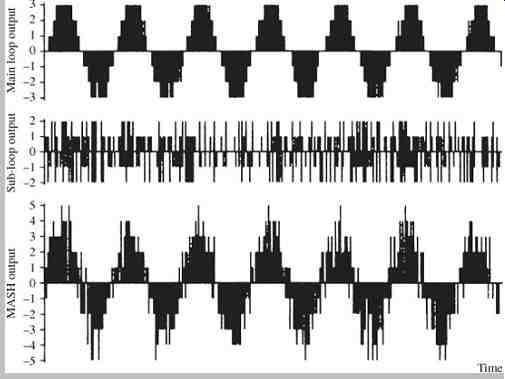
FIG. 11 A graphical representation of the data values in a multistage noise
shaper.
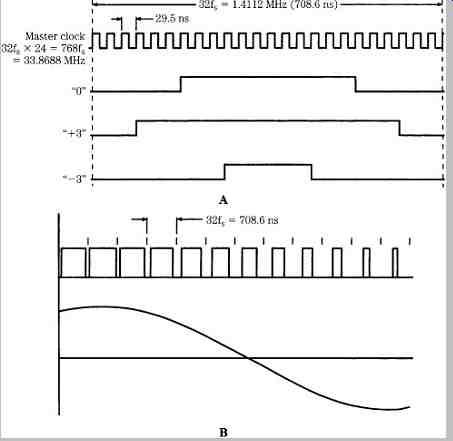
FIG. 12 Pulse-width modulation data is output from a MASH converter. A. Examples
of pulse-width modulation data. B. Reconstruction of the analog waveform.
The final element in the system is D/A conversion. The 11-valued signal is converted into pulses, each with a width corresponding to one value, as shown in FIG. 12A. This can be accomplished by applying the 4-bit output of the shaper to a lookup table to map 11 amplitude steps into 22 time steps with constant amplitude. For example, the figure shows the PWM waveforms resulting from the 0, +3, and -3 output values. In actuality, waveforms representing ±5, ±4, ±3, ±2, ±1, and 0 are all output. The widest pulses translate into a large positive output, and the narrowest pulses translate into a large negative output, as shown in Fig. 12B. The width of the pulses carries the vital information; the amplitude of this signal can only be high or low. At this point the signal has the form of PWM binary data. Because timing accuracy can be achieved through crystal oscillators, the widths are very accurate, and hence signal error is low.
The relatively coarse quantization permits accurate pulse timing by synchronizing pulse edges to the oversampling clock. Positive- and negative-going pulses are output, to cancel common noise. This 33.8688-MHz (768 × fs) data forms a PWM representation of the waveform; FIG. 13 shows the spectrum of a 20-kHz input signal. Proof of performance can be evaluated by measuring the in-band noise of the system; it is below -100 dB. FIG. 14 summarizes the mathematical basis of third-order noise shaping.
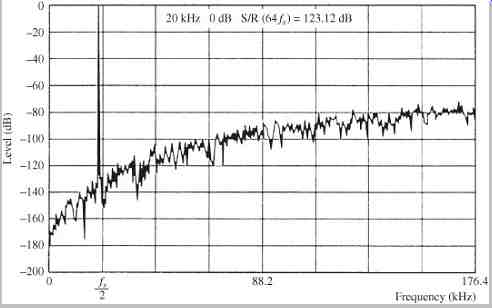
FIG. 13 Reproduction of a 20-kHz waveform showing the effect of third-order
noise shaping.
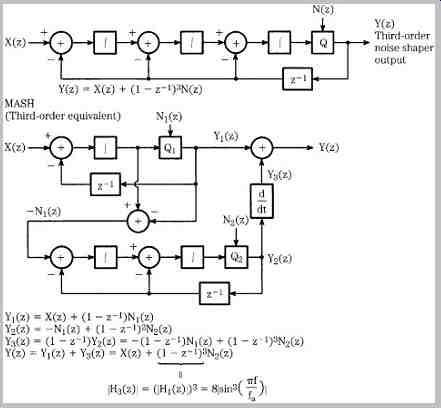
FIG. 14 Analysis of a third-order noise shaper.
Multi-Bit D/A Conversion with Quasi Fourth-Order Noise Shaping
Victor Advanced Noise Shaping (VANS) is an example of a multi-bit D/A converter architecture using eight-times oversampling, a quasi fourth-order noise shaper, and pulse-edge modulation conversion. The noise shaper uses four loop filters in a configuration that yields in-band performance equivalent to fourth-order noise shaping. The VANS circuit is designed to operate like a fourth-order noise shaper at audible frequencies, gradually shifting toward second-order noise shaping at higher frequencies.
This provides stability, yet improves performance in the audio band.
Thirty-two times oversampling is performed, and the output clock frequency is 16.9344 MHz (384 × fs). With pulse-edge modulation, input data is converted into a binary pulse train with 15 discrete values (±7, ±6, ±5, ±4, ±3, ±2, ±1, 0). A differential configuration is used in which the rise of the leading edge of a pulse, and the fall of the trailing edge of a pulse, are output by two independent pulse-edge modulation converters. This determines the width of the pulse. Two converters output pulse trains based on the input signal, and an analog subtractor generates a composite signal determined by the leading and trailing edges of the pulse trains. This signal can take either a positive or a negative value. For example, data representing a -1 value would generate a short negative going pulse, but data representing a +5 value would generate a longer positive-going pulse. When time averaged, these values create the analog waveform, as in pulse-width modulation. FIG. 15 summarizes the mathematical basis of this quasi fourth-order noise shaping.
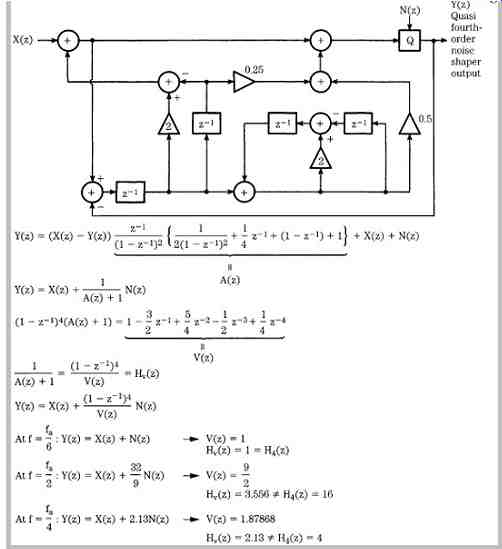
FIG. 15 Analysis of a quasi fourth-order noise shaper.
Generally, even higher orders of noise shaping can be successfully employed, yielding very low in-band noise floors. For example, a fifth-order sigma-delta modulator is used in some Direct Stream Digital (DSD) encoders used in the Super Audio CD (SACD) format. (cont. part 2)