Scope waveforms are valuable for much more than merely revealing the waveshapes of signals. The March and April scope tips articles pointed out measurements of dc voltages and frequencies as two scope capabilities that should be employed more often. Most of the information this month is about identifying and locating zero and average lines in any waveshape. Some of the July coverage will include analyzing familiar waveforms in a new way.
By Gill Grieshaber, CET
Clamping & clipping sine waves
A sine wave by definition is a signal having only one frequency; a fundamental without harmonics. Many RF signals have a sine waveshape. The power-line wave form should be made up of sines. Most explanations of waveshapes begin with sine waves.
Unfortunately, some important facts about these waveforms are not emphasized enough. One such fact is the location of the average-voltage line. Others are the functions and values of this line.
Another important parameter is the location of the zero-voltage line. Sometimes the average-voltage and the zero-voltage lines are located at the same point, but not always! It depends on another factor, which will be explained later.
Fortunately, any scope that has both ac and dc coupling in the vertical amplifier can reveal the location of both these lines. And a scope with only ac coupling can show the average-voltage line automatically!
A tale of two lines
Coupling capacitors and signal-coupling transformers pass the ac signal but remove any steady dc level. Therefore, the output signal from either T1 or C1 in Figure 1A will be a sine wave when the input is supplied with a sine wave, and neither can pass any permanent dc voltage. That's why a scope cannot respond to dc voltage when it is operated in the ac mode. However, some important information can be obtained by using those ac and do scope modes alternately.
Both of the Figure 1B sine waves have an imaginary average-voltage line running horizontally through the exact center of the waveshape. How can that be proved with an ac-coupled scope? Just remove the scope signal and the horizontal line that results will be located precisely where the center of the sine wave had been before. And because the line is caused by a lack of any voltage, it is called the zero-voltage line.
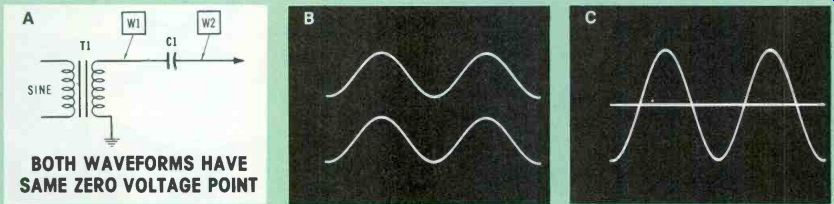
Figure 1 (A) BOTH WAVEFORMS HAVE SAME ZERO VOLTAGE POINT The isolated secondary
of a coupling transformer and a coupling capacitor both pass a replica of
the input waveform but each removes any steady dc voltage. (B) A dual-trace
scope proves the sine signals at the W1 and W2 test points have the same waveshape
and amplitude. (C) When the scope is set for ac coupling, removing the sine
signal produces just a horizontal line. This is the zero-voltage line since
it is generated by zero voltage. A sine wave is symmetrical; therefore, a
line across the exact center represents the average voltage. In this case,
both zero and average-voltage lines have the same location. Remember this
rule: When no dc voltage is present, the zero-voltage and average-voltage
lines are the same.
This action can be proved by several methods. Alternately connecting the sine wave signal and then removing it will show both waveforms in rapid succession (if the scope locks fast enough). A permanent record is obtained by one photographing the line and the sine with two exposures (many of the ES waveforms are made in this way).
The best way is to use a dual-trace scope. With no signal applied to either channel, move both horizontal lines to the center line of the scope so the two become just one.
Then apply the sine wave to one channel. The resulting combined waveforms are shown in Figure 1C.
But, wait a minute. The original intent was to find an average-voltage point or line, and the previous method found only the zero-voltage line. No doubt there is a mathematical method of proving both are the same, but it's easier to use a bit of common-sense logic. Sine waves are symmetrical. Therefore, it follows that the top and bottom halves are precisely equal, so the average line must be across the exact center.
The zero-voltage line and the average-voltage line both extend across the exact center of a sine wave. This permits the first import ant tip: When no dc is present, the zero and average-voltage lines are the same.
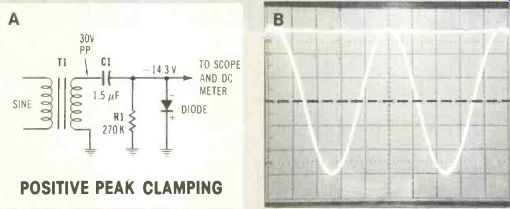
Figure 2 (A) When connected after a coupling capacitor, a diode can
clamp the tip of either the positive or negative peak to any selected
dc voltage. The positive peak is shown clamped to zero voltage (ground).
(B) The dc scope waveform locates the zero line just barely below the
positive tips. (When the dc mode is selected, center the scope waveform
and then remove the input signal.
The resulting line is zero voltage.) However, the average-voltage line remains at the waveform center, marked here by a dotted line. Since the top line represents zero, the average line must be in a negative area. And the number of graticule divisions shows the voltage. Each scope division is 5 V; therefore, this wave form should measure slightly less than-15 V on a dc meter (it measured-14.3 V). The zero line is 0.6 V below the extreme tip, and this subtracts from what should have been a-15 V reading (if the diode had no voltage drop). This experiment verifies the following rule: The scope reading between the zero line and the average-voltage line equals the dc voltage measured by a meter. POSITIVE PEAK CLAMPING

Figure 3 (A) This schematic is identical to Figure 2A except for the
diode polarity which clamps the negative peak to produce positive dc
voltage. (B) Dc scope operation verifies the location of the zero-voltage
line at about 0.6 V above the negative tips, and ac operation shows the
average line is at the center (marked by dotted lines). Slightly less
than 3 scope divisions are between the two lines. This is a bit less
than +15 V at 5 V/div, and the reading agrees with the Figure 2 rule.
(C) When the sine-wave source has poor regulation, the diode current
flattens the tip as shown. This flattening causes errors, so a better
signal source should be used for all experiments. NEGATIVE PEAK CLAMPING
Sine waves with dc voltage
Addition of a diode can clamp the ac signal to a desired dc voltage. Figure 2A shows clamping to zero voltage. Transformer T1 provides a low impedance for the circuit that follows. The C1 capacitor prevents loss of any dc voltage through the transformer, and the large capacitance prevents loss of signal amplitude at the circuit output.
Because the anode of the diode is toward the sine wave, the diode will conduct whenever the positive peak is there, and it cannot conduct when the negative peak is present.
In reality, the circuit is a peak-reading shunt rectifier (which will not be explained here). C1 stores a charge that prevents conduction of the diode except at the extreme tip of each positive peak.
The diode cathode is grounded.
Therefore, each sine wave positive tip is grounded during conduction of the diode. Logic says this point of conduction must be zero voltage.
The dc waveform of Figure 2B proves the truth of that assumption.
However, the previous analysis revealed that both the average and zero lines extended across the same exact center when no dc was present. But now the zero line is not at the center. Does this hint that dc has been produced? If so, how much dc? And where is the average-voltage line? Voltage measurements can be used to answer those questions.
When 30 VPP reached the diode through C1, a dc meter measured exactly -14.3 V dc. When the 0.7-V drop across the diode is added, the total is -15 V, which is exactly half of the sine wave peak-to-peak reading.
The average-voltage line remains at the center of the sine wave, so it and the zero line are separated by 15 V peak-to-peak. Again, this is half of the sine-wave amplitude.
The dc-voltage reading and the peak voltage between the zero line and the average-voltage line are both equal to half of the total sine-wave amplitude.
Therefore, under the stated conditions, this second important rule also must be true: The peak voltage between the zero line and the average line equals the measured dc voltage. In the previous example when no diode was present, the peak voltage between the lines was zero and the dc voltage measured zero. The new rule proved to be correct for both examples. Is it valid for other wave shapes? The question will be answered later.
Several additional facts are proved. When the positive peak is clamped to zero volts, all of the waveform (except the 0.7 V for the diode) is negative. Therefore, clamping the positive peak produces negative do voltage (which is equal to half of the waveform amplitude for sine waves).
Figure 3A schematic and the Figure 3B waveforms prove that clamping the negative peak also produces the same results, except the do voltage is +14.3 V.
An unsuccessful measurement is illustrated by the Figure 3C wave form where the signal source was a sine/square generator having an output impedance so high that the diode load flattened the negative tip. The flattened tip introduced one error and the low-level output (12 VPP) caused the diode voltage drop to be more significant by comparison. The total effect of both errors reduced the accuracy of the experiment too much for it to have any value. In Figure 3B, the same generator was used, but a powerful amplifier was added between it and the peak-clamping circuit.


-------------
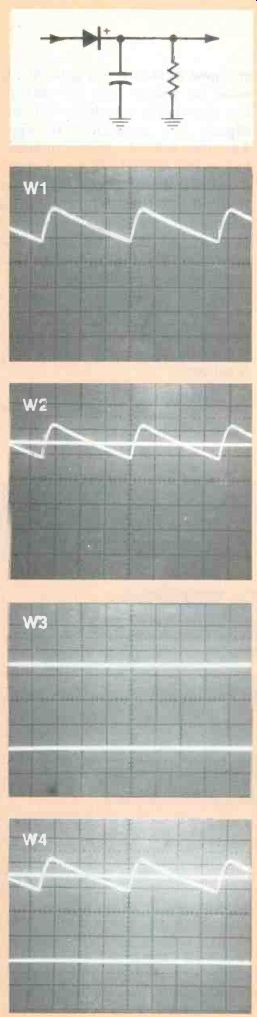
Three separate exposures were made by covering two-thirds of the scope screen each time. The centering was not changed. Vertical lines have been touched up to make them visible. This picture shows how pulse waveforms position themselves on the average-voltage line according to the duty cycle. The drawings show that the clamping zero line is spaced from the peak tip by the 0.6 V diode voltage. Therefore, all dc voltages are decreased by 0.6 V. (Also, the drawings illustrate Figure 5C.)
--------------
Positive and negative peaks
All ac waveforms have two peaks for every cycle. The positive peak by definition is the positive portion of one cycle, and the negative part of the same cycle is the negative peak. Unfortunately, conventional scope waveforms give no hint about where one peak ends and the other begins. With pulses, jagged waveshapes and other non-sinusoidal waveforms these peak locations are not obvious. And yet a point of zero voltage must exist between adjacent positive and negative voltages. How can this zero point be found on scope waveforms? A diode has no difficulty when locating the zero-voltage point in a signal.
During rectification of an ac voltage, a diode operates only on the voltage between the zero point between the peaks and whichever peak represents forward bias to it. In other words, a diode rectifies the voltage of one peak while ignoring (as though it is not present) the reverse-polarity voltage on the other side of the mysterious zero point. Many other devices and circuits operate from the same zero point, and do it automatically. A scope is one of these.
Scope produces only one line
The DC/GND/AC switch on the scope panel shorts across the input coupling capacitor when at the dc position, thus allowing any dc of the signal to pass through the direct-coupled vertical amplifiers. The ground position disconnects the incoming signal and grounds the input of the vertical amplifiers.
Operation of this coupling switch can produce a line either at the zero-voltage point (for dc operation) or at the average-voltage point (for ac). The difference is made possible by the input coupling capacitor. Inside the scope beyond the capacitor, the circuit can furnish a line only at the zero-voltage point.
Measuring a power supply
The basic principle should be made clear by the following method. It can be performed with a single-trace scope, but it is easier to understand in dual-trace.
Objectives of these measurements are to determine the amount of dc voltage (using zero and average lines) and the ripple amplitude of the power supply shown in the schematic. (The supply output was +17 Vdc and 7 VPP of ripple.
Less ripple or higher dc decreases the visibility, but does not change the accuracy.) With both probes connected to the supply output, one channel is set for dc coupling and the other for ac. While using the same channel sensitivities (5 V/div here), merge the two waveforms in the upper section of the screen, and make certain the amplitudes are identical so only one waveform (W1) is displayed. This merged waveform is the ripple sawtooth, which can be measured in the usual way.
For the channel with ac coupling, move the switch to the center (ground) position. One sawtooth waveform changes to a line through the approximate center of the sawtooth waveform from the other channel (W2). This line represents the average voltage of the sawtooth waveform (ac).
Next, move the other-channel coupling switch (formerly at dc) to the ground position, which changes the last sawtooth waveform into a line near the bottom of the screen. It represents the location of zero voltage for dc operation.
The two lines of W3 now are the only waveforms on the screen. Measure the peak-to-peak (or peak) voltage between them. That value is equal to the dc voltage from the power supply.
This is another example of the rule proposed in the article, which states: The peak-to-peak reading between the average-voltage line and the zero-voltage line equals the dc voltage as measured by a dc meter.
Finally, W4 shows the ripple and the two lines as they would appear on a three-channel scope.
--------------
Clipped sine waves
The resistor/diode arrangements of Figure 4A will clip (remove) the negative peak (leaving positive do voltage and the positive peak)-or will clip the positive peak, which produces negative do voltage and leaves the negative peak untouched.
Remember that the part of a sine wave above the average-voltage center line is called the positive peak, and similarly the part of a sine wave below the average-voltage center line is called the negative peak. The transformer removes any permanent do voltage or current, and there is no capacitor to allow peak-reading rectification. There fore, in the top schematic, the negative peak is forward bias for the diode, which conducts thus causing a short (except for the 0.6 V drop across the diode) during the time of the negative peak. This is shown by the top waveform of Figure 4B (along with the true zero-voltage line). With 30 V peak-to-peak from the transformer, the output voltage as measured by a do meter was +4.3 V. After the 0.6 V drop of the diode is added, the theoretical output voltage is +4.9 V. In the top waveform of Figure 4B, the clipped peak of the sine wave measured 15 V peak-to-peak.
The average-voltage line (about a third of the way from the bottom of the waveform) was placed by using ac scope coupling, while the zero line at the bottom was produced by the dc scope function. Between the two lines is about 5 V peak.
Average voltage-for full-wave clipped sines is 63.7% of the peak voltage; for half wave, it is 31.8% of the peak voltage. And +15 V multiplied by 31.8% equals +4.8 V dc.
--------------------
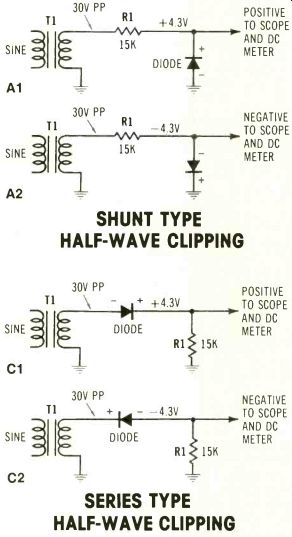
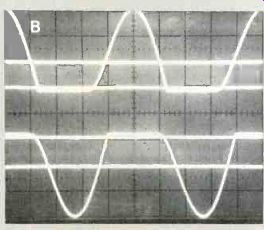
Figure 4 A diode and a resistor can remove one sine-wave peak by clipping.
(A1) The negative peak is removed by diode conduction, leaving only positive
half cycles that measure as positive dc voltage. (A2) When the diode
polarity is reversed, the positive peak is clipped, leaving only negative
peaks that measure as negative do voltage. (B) The top waveform was obtained
from the Al circuit, while the bottom waveform came from the A2 circuit.
In the top waveform, notice that a small bit of the negative peak (below
the zero line) is not removed. That's because a silicon diode must have
forward bias in excess of 0.6 V before full conduction can occur.
This small amount of undesired peak subtracts from the dc voltage, which otherwise would measure +15 V. (C) These series clipping circuits also remove one peak because the diode does not conduct until it is supplied with more than 0.6 V of forward bias.
Therefore, 0.6 V is removed from the waveform near the zero-voltage point. This can be proved by careful scope measurements. The waveforms of B verify the rule given in Figure 2, and also that the average-voltage line is correctly located at 31.8% of the half-wave amplitude.
SHUNT TYPE HALF-WAVE CLIPPING; SERIES TYPE HALF-WAVE CLIPPING
--------------------
Three methods produced a figure for the dc voltage. According to calculations for half-wave rectification, the voltage was +4.8 V. The measured output voltage plus voltage drop of the diode totaled +4.9 V. And the dc voltage according to the peak voltage between the zero-voltage line and the average-voltage line was about +5 V dc.
This similarity of results proves the scope method of placing the average-voltage line is valid, with the only inaccuracies coming from the usual problems of reading scope waveforms.
The bottom schematic corresponds to the bottom waveform trace in Figure 4B where the positive peak is clipped (shorted out) by the diode and leaving 15 V peak-to-peak and a measured-4.3 V dc.
If the resistor and diode are swapped as shown in Figure 4C, the same dc voltage will be obtained, but the visible waveform will have slightly less amplitude. In Figure 4A, the 0.6 V (that's necessary before the diode begins to conduct) protrudes beyond the zero line, while the Figure 4C version does not permit any output waveform to be visible on the scope screen until after the diode 0.6 V has been overcome and conduction begins.
So, the conclusion is that both the zero-voltage line and the aver age-voltage lines can be placed accurately by the dc and ac scope functions.
The next important question is this: Are the previous two rules-of-thumb accurate when applied to pulses of various duty cycles and to square waves?
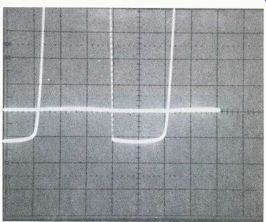
When the Figure 4B top waveform is made taller by changing to 0.5 V/div,
the part of the negative peak that extends below the zero line is very
plain. It measures 0.6 V, which is the amount of silicon-diode forward
bias that is ignored by the diode.
Measuring & clamping pulses
Pulses represent the worst obstruction to a complete acceptance for the two rules proposed so far. If they accurately describe the dc levels obtained by clipping or clamping pulses, then those rules are worthy of being generally accepted. Pulses can assume almost an infinity of shapes. Some pulses have squared tips, others have sloping sides and rounded tips. And the duty cycle (ratio of on time to off time) can be nearly any value.
In fact, square waves can be considered as pulses with a 50% duty cycle.
To reduce these many variables to a manageable number, just a few examples are illustrated by square-tipped pulses from a VIZ model WR-549A pulse generator.
Note: All measurements of pulses and square waves are made with the circuits of Figure 5A. However, the dc voltages listed there apply only to the 1-to-10 ratio pulses.
Measuring square waves--If the clamping diode of Figure 5A is disconnected and a square wave is applied to the input, the dc and ac functions of a scope will show both the zero-voltage and average-voltage lines extended across the exact center of the square wave (Figure 5B).
According to the rules proposed earlier, this indicates an absence of any dc voltage. A test with a dc meter verified the lack of dc.
When the negative peak was clamped by connecting the diode cathode to the ac signal, the average-voltage line remained at the center (the waveshape was not distorted), but the zero-voltage line then was located at the tip of the negative peak, as shown by Figure 5B.
A scope measured a peak reading of 6 V between the two lines.
Therefore, the dc voltage should have been +6 V. A dc meter checked +5.5 V. After addition of the +0.6 V of diode drop, the total was +6.1 V. The scope reading of +6 V compares very favorably.
Both sine and square waves are symmetrical, and both responded to the proposed rules about the zero and average lines. This hints that all symmetrical waveforms will respond in the same way. Other experiments have verified this assumption.
------------------

Figure 5 --- Pulses can be clamped by the same method used before with
sine waves. However, the pulse polarity affects the dc voltages. (A1)
The negative peak is clamped, so all dc voltages will be positive.
The do voltages shown apply only to the 10-to-1-ratio in Figure 5E.
(A2) Reversing the diode polarity clamped the positive peak, so all
dc voltages are negative. Notice that the pulse polarity affects only
the amount of dc voltage; polarity of this do is determined solely
by the diode polarity. (B) Pulses of 50% duty cycle (same time on as
off) are square waves. The vertical lines have been touched up to make
them visible and a zero line is indicated by a dotted line. This waveform
is symmetrical, so +5.4 V were measured in Figure 5A1 and-5.4 V were
the reading in Figure 5A2. (C) Different positive and negative readings
are obtained when the duty cycle is 66% (on time is 2X and off time
is 1X) as shown by the top waveform.

The top waveform in the A1 schematic produced +3.4 V, while in the A2 schematic the reading was -7.4 V. The bottom waveform produced +7.4 V in the A1 schematic, and the same waveform applied to the A2 schematic produced-3.4 Vdc. (D) The 5-to-1 pulse ratio causes even larger differences between dc readings of the two polarities. The top waveform in circuit Al produced +1.5 V, and-9.3 V in circuit A2. Circuit A1 and the bottom waveform measured +9.3 V, with circuit A2 producing-1.5 V.
After all readings were increased by 0.6 V for the diode, they were 2.1 and 9.9 V for a total of 12. This matches the 12 VPP at the circuit. A slight error of pulse width accounts for the small discrepancy. (E) Proper polarity differences with a 10-to-1 ratio should produce basic readings of 1.1 and 10.9 voltages after the diode voltage is considered. That was true in this case also. A.NEGATIVE PEAK CLAMPING ; POSITIVE PEAK CLAMPING
-------------------
Why must allowances be made for the diode voltage drop? All diodes reduce power supply voltages, for example, but the reduction often is overlooked because a drop of less than a volt out of several hundred is not significant.
But it is important in teaching situations such as these where purity of waveform is more important than a high signal amplitude.
Measuring 33% duty-cycle pulses---Figure SC pictures 66% duty-cycle pulses at the top and 33% duty-cycle pulses at the bottom. Graticule markings are shown, along with the average-voltage lines.
Rectification of these two inverted waveforms in the circuits of two polarities in Figure 5A should produce four different dc voltages, if the rules previously given are correct.
Those examples of average-voltage lines presented before involved symmetrical waveforms where it was obvious that the same voltages were present in each peak and the line must be at the center. But with pulses, this relationship no longer is valid. Figure 5C has another obvious relationship: A certain voltage for one length of time equals half as much voltage that is there for twice the amount of time.
This logical assumption indicates that a scope can position the average-voltage line (even if it has pulses or irregular areas) both correctly and automatically, thus making it unnecessary to calculate the line position. From here on, therefore, the accuracy of average-voltage. lines will be accepted, and no attempt will be made to explain or justify the use of a line produced by the scope.
Figure 5D gives the waveforms and measured voltages for 83% and 17% duty cycles (5:1), and Figure SE does the same for 90.9% and 9.1% duty cycles (10:1). Notice that the theoretical and measured voltages (after correction for diode drop) are almost identical.
Absorbing (?) pulses
Statements about transient protection sometimes include a sentence that says capacitors absorb part of the pulses. Figure 6A is the schematic of a circuit used to test the truth of that statement, while the waveforms in Figures 6B and 6C showed the changes when various values of capacitors were used for C1.
The average-voltage line is shown for each waveform. And because this is an ac application, the zero line is identical to the average line. At the beginning of the sequence, the positive-going pulses had far more amplitude than the negative peaks showed. After strong filtering (last waveform), the amplitude was reduced and the waveshape approached a rounded sawtooth.
However, the pulses were not absorbed but instead were merely integrated by the RC time constant. Remember the time-constant curves presented several months ago? Well, the second and third wave forms are made up of voltage charging and discharging curves for different amounts of time. Basic theory can explain almost any electronic phenomena if it is completely and correctly applied.
Comments
All ac voltages were stated in peak or peak-to-peak values. This was done deliberately because it is the only way correct answers can be obtained regardless of the wave shapes. Technicians should begin to measure all ac voltages in peak and peak-to-peak, and then use scopes to show average and zero lines when it's necessary to predict the amounts of dc voltage that should be produced by those particular waveforms.
A summary of the helpful rules about zero and average lines follows:
When no dc is present, the zero-voltage and average-voltage lines are the same. Conversely, when the lines are separated, dc voltage must be there.
Peak voltage between the zero line and the average-voltage line equals the measured dc voltage plus any diode voltage drop. (Of course, where defects exist, that is what the dc voltage should measure.)


Figure 6---A low-pass RC circuit (A) is formed by the resistances of
wires, switches and transformers. (Inductive effects of tie pole transformers
add LC sections which produces much more filtering.) This sequence
of waveforms shows changes that occurred to the sharp pulses as the
C1 capacitor value was increased in steps. Instead of being absorbed
by the capacitor, the pulses were integrated so the amplitude was decreased
without any change of total power. The third waveform shows unmistakable
voltage charging curves on the leading edges and voltage-discharging
curves on the trailing edges. CAN CAPACITORS ABSORB PULSES?
Next month
Different rectifier performances between fast-recovery diodes and conventional 60-Hz diodes are to be shown in special waveforms.
The principles of the zero and average lines will be applied to the grid signal of horizontal-output tubes and the waveforms in tube-type vertical sweep circuits.
Also see: A second look at waveforms--part 2
Better waveforms with wideband scopes