Simple systems
Conversion from digital to analog signals must use methods that are suited to the type of digital signal that is being used. If, for example, we were using simple digital amplitude modulation, or even a system in which the number of l's were proportional to the amplitude of the signal, then the conversion of a digital signal to an analog signal would amount to little more than smoothing, as Figure 4.1 illustrates. As it happens, it is possible to convert a digital signal into a form that can be smoothed simply, and this is the basis of bitstream methods, as we shall see later. For the moment, however, we shall concentrate on the earlier methods.
Pulse amplitude; Pulse width; Pulse number; Integrator; Audio (smoothing 1 circuit) output
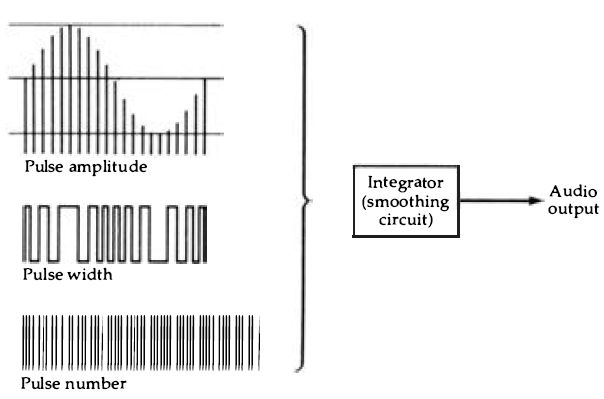
Figure 4.1 Three types of digital modulation that can be converted back to
analog simply by smoothing. None of these is really suitable for digital audio,
although the pulse-number system could be very useful if it did not require
such a large number of pulses for each number (up to 65535) .
Output from D-A converter
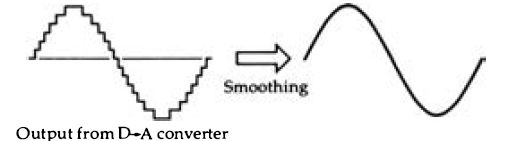
Figure 4.2 The use of smoothing in D-A conversion. A small amount of smoothing
will remove the steps from the signal, but a good low-pass filter is better
in this respect.
Smoothing always plays some part in a digital to analog conversion, because a converted signal will consist of a set of steps, as Figure 4.2 shows rather than a smooth wave (is any audio signal a smooth wave?) . With a sampling rate of the order of 44 kHz, however, the steps are close spaced, and very little smoothing is needed. Even a crude resistor-capacitor smoothing circuit can work wonders with such a wave, and the more complex integrators can reproduce a signal whose amplitude at any point follows closer to the original than is possible when a purely analog recording method has been used. The faster the pulse-rate of the output of the D-A converter, the easier it is to smooth into an acceptable audio signal . The pulse code type of digital system does not allow a set of digital signals to be converted into an analog signal by any simple method, however, which disposes of any dreams of driving a loudspeaker directly from such signals . Remember that the digital signal consists of a set of digitally coded numbers which represent the amplitude of the analog signal at each sampling point . For conversion, then, we need circuits that will convert each number into a voltage amplitude that is proportional to that number. The alternative, which would allow for driving loudspeakers directly, would be to convert each digital number into a set of pulses equal to that number, so that a 'l' would give one pulse, and a 65536 would give 65536 pulses. One minor problem with such a system would be that since negative numbers could not be catered for, the path from the smoother to the output stage would need to include a capacitor or transformer to remove the DC level . The alternative would be some kind of bias arrangement . As it happens, bitstream methods bring all this a little closer . The nature of the conventional conversion requirement is more easily seen if we illustrate it using a four-bit number. In such a ...
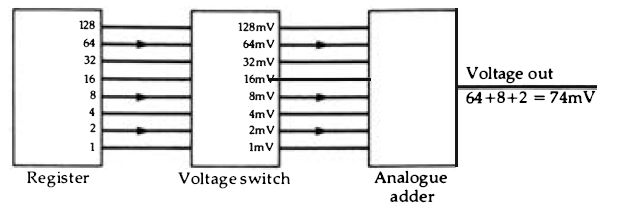
Figure 4.3 The principle of the weighted converter. Each output from the
register operates a voltage switch, with the voltages arranged to be in the
ratio of powers of two. By adding the voltages, the amplitude of the analog
signal is recovered.
... number (like any other binary number), each 1 bit has a different weighting according to its position in the number, so that 0001 represents one, 0010 is two, 0100 is four and 1000 is eight . The progression is always in steps of two, so that if we could connect a register to a voltage generator in the way illustrated in Figure 4.3, each 1 bit would generate a voltage proportional to its importance in the number. In this way, a 1 in the second place of a number would give, say, 2 mV, and a 1 in the 4th place would give 8 mV, with a 1 in the 7th place giving 64 mV. Adding these voltages would then provide a voltage amplitude proportional to the complete digital number, 74 mV in this simple example . This, in essence, is the basis of all D-A converters.

Figure 4.4 The voltage adder stage of a weighted converter, shown for four
bits only. The stage is an operational amplifier with switched resistors in
the feedback path. The drawbacks of the system are the huge range of resistance
values and the requirement for very close tolerance, particularly for the
larger values.
Reverting to a four-bit number, Figure 4.4 shows the basis of a practical method . Four resistors are used in a feedback circuit which makes the output of the buffer amplifier depend on the voltage division ratio. This in turn is determined by the resistor ratio, so that switching in the resistors will give changes in voltage that are proportional to resistor value. In this example, each resistor can be switched into circuit by using an analog switch, and the switches are in turn controlled by the outputs from the bits of a parallel output register . If the highest order bit in the register is a 1, then, the resistor whose value is marked as R is switched in, if the next bit is 1, then resistor 2R is switched in and so on.
The result of this is that the voltage from the output of the buffer amplifier (an analog adder circuit) will be proportional to the size of the digital number . We can at the moment ignore the effect of negative numbers because they can be dealt with by altering the voltage that is switched in with the highest order of bit - the principle of how the converter works is not affected. The attraction of this method is its simplicity -- and that is also its main problem.
The resistor switching type of converter is widely used and very effective - but only for a limited number of bits . The problems that arise are the range of resistances that are required, and the need for quite remarkably precise values for these resistors . Suppose, for example, that we considered a circuit in which the minimum resistance that we could use was around 2K. This is a reasonable value if we assume that the amplifier has an output resistance that is not negligible and that we have to use resistance values that will be large compared to the resistance of the analog switch when it is on. Now each resistor in the arrangement will have values that rise in steps of two, so that we shall have 4K, 8K, 16K ... all the way to 256K for an eight-bit converter.
Even this is quite a wide range, and the tolerance of the resistor values must also be tight . In an eight-bit system, we would need to be able to distinguish between levels that were one 256th of the full amplitude, so that the tolerance of resistance must be better than one in 256 . This is not exactly easy to achieve even if the resistors are precisely made and hand-adjusted, and it becomes a nightmare of difficulty if the resistors are to be made in IC form.
The problem can be solved by making the resistors in a thick-film network, using computer-controlled equipment to adjust the values, but this, remember is only for an eight-bit network.
When we consider a sixteen-bit system as we must use for digital audio, the conversion looks quite impossible. Even if we drop the minimum resistance value to around 1-K, the maximum will then be of the order of 65M, and the tolerance becomes of the order of 0.006%. The speed of conversion, however, can be very high, and for some purposes a sixteen-bit converter of this type would be used, with the resistors in thick-film form. For any mass-produced application, however, this is not really a feasible method. The requirement for close tolerance can be reduced by carrying out the conversion in four-bit units, because only the highest order bits require the maximum precision.
Incidentally, these converters and the current converters that are described below, all work with positive values only. This means that the digital numbers, though coded in normal form, need to be interpreted differently, and the convention is that the binary zero number (sixteen zeros) will be represented by half of the maximum possible voltage or current, and that positive values correspond to having the most significant bit set, the opposite of the digital convention. This amounts to nothing more than the digital equivalent of bias and inversion.
Current addition The alternative to adding voltages is the addition of currents . We can, of course, regulate currents with resistor networks, and though the values of the resistors that we can use are more acceptable, the requirement for high precision is just as it is for the voltage addition method if we follow the same pattern as the voltage converter. We can, however, consider something rather different . Instead of converting a sixteen-bit number by adding sixteen voltages of weighted values (each worth twice as much as the next lower in the chain), we could consider using 65535 current sources, and making the switching operate from a decoded binary number.
Once again, it looks easier if we consider a small number, three digits this time, as in Figure 4.5. The digital number is 'de-multiplexed' in a circuit which has eight outputs . If the digital number is OOO, then none of these outputs is high, if the digital number is 001 then 1 output is high, If the digital number is 010, then two outputs are high and if the digital number is 011 then three outputs are high, and so on. If each output from this demultiplexer is used to switch in an equal amount of current to a circuit, then the total current will be proportional to the value of the binary number.
The attraction of this system is that the requirement for precise tolerance is much less, since the bits are not weighted. If one current is on the low side, then another is just as likely to be on ...

Figure 4.5 Current addition method . The demultiplexer has as its input the
binary signals (3 lines in this case) and as its outputs a set of lines. Each
binary input causes a corresponding set of outputs to go high, so that a 001
input makes one line high, and a 101 input makes 5 lines high. The demultiplexer
outputs are used to operate current generators, each contributing one unit
of current to an adder stage (not shown separately). Example: 101 into demultiplexer causes five outputs, hence five units of
current ...
… the high side, and the differences will cancel each other out, something that does not happen if, for example, the one that is low is multiplied by 2 and the one that is high is multiplied by 1024. The effort of constructing 65535 current supplies, each switched on or off by a number in a register, is not quite so formidable as it would seem when you think of what can be done with ICs nowadays . It still amounts to rather more components than could comfortably and reliably be made in IC form when digital audio was in its early stages, though, and compromises are needed to cut down the number of components . The main compromise is in the number of currents. Instead of switching 65535 identical current sources in and out of circuit, we choose a lower number and make the currents depend on the place value of bits. Suppose, for example, that we settled for 16383 currents, but that each current could be of 1, 2, 4, or 8 units . The steps of current could be achieved by using resistors whose precision need not be too great to contemplate in IC form, and the total number of components has been drastically cut, even if we allow for the more difficult conversion from the digital sixteen bit number at the input to the switching of the currents at the output.
This is the type of D-A converter that is most often employed in CD units.
Another possibility is to use a current analog of the resistor switching method used in the voltage step system, so that the currents are weighted in 2:1 steps, and only sixteen switch stages are needed . This is feasible because we can make current dividers ...

Figure 4.6 The principle of a current divider . If you think of it as a current
adder, the action looks simpler.
... in IC form, using semiconductors. The principle of a current divider is shown in Figure 4.6 with currents shown as flowing into the terminals at the top rather than out - the distinction between a current adder and a current divider is a matter of which direction of currents you are interested in! To act as a precise divider, however, the input currents must be identical to a very close tolerance, and this cannot be achieved by a resistive network alone .

Figure 4.7 The simple current divider (a), and the development of this with
switching (b) . By switching at a high speed, the division can be almost perfect
providing that the clock pulses are at precisely equal intervals, and that
the switching transients are smoothed out.
In this form of converter, then, first described by Plassche in 1976, the resistor network is used along with current switching.
The principle is shown in Figure 4.7, and is easier to think of if you regard it at first as a current adder rather than a divider. The two input currents 11 and 12 form the current 13, and if the resistors R1 and R2 are precisely equal, then I1 =I2=I3/2, giving us the condition that we require of a current (I_1 or I_2) being exactly half of the other current 13. The snag, of course, is that resistors R1 and R2 will not be identical, particularly when this circuit is constructed in IC form.
The ingenious remedy is to alter the circuit so that each current is switched so that it flows alternately in each resistor. For one part of the cycle, I1 flows through R1 and I2 through R2, then in the other part of the cycle, I1 flows through R2 and I2 through R1 . If the switching is fast enough and some smoothing is carried out, the differences between the resistor values are averaged out, so . that the condition for the input currents I1 and I2 to be almost exactly half of 13 can be met even if the resistors are only to about 1 % tolerance. Theory shows that the error is also proportional to the accuracy of the clock that controls the switching, and this can be made precise to better than 0.01% with no great difficulty.
Now if we consider a set of these stages connected as in Figure 4.8, we can see that the ratio of currents into the stages follows a 2:1 step, and this can be achieved without a huge number of components and without the requirement for great precision in anything other than a clock signal . In addition, the action of the circuit can be very fast, making it suitable for use in the types of A-0 converters that were discussed in section 3. The only component that cannot be included into the IC is the smoothing capacitor that is needed to remove the slight current ripple that

Figure 4.8 The principle of a step-type of current divider, which gives a
set of currents that are in the correct ratio for a D-A converter.
will be caused by the switching. This can be an external component connected to two pins of the IC. The level of conversion is another point that needs to be considered. If we take a voltage conversion as an example, then the amplitude of the signal steps that we use will determine whether the peak output is 10 mV, 100 mV, 1V or whatever. The higher the peak output, the more difficult is the conversion because switching voltages rapidly is, in circuit terms, much simpler when the voltage steps are small, since the stray capacitances have to be charged to lower levels . On the other hand, the lower the level of the conversion, the greater the effect of stray noise and the more amplification will be needed. A conversion level of about one volt is ideal, and this is the level that is aimed at in most converters . Conversion problems The problems that arise with the conventional type of D-A converter are closely connected with the nature of the digital signal and the ever-present problems of precise current generation. A 16 bit D-A converter requires the use of 16 current sources, and the ratio of a current to the next lower step of current must be exactly 2. For a conventional type of current generator system in which the current source provides current I, the most significant bit will be switching a current equal to 112 and the least significant bit will be switching a current equal to 1165536. With all switches open (all bits zero) the current will be zero; with all switches closed (all bits 1) the current will be equal to 1 - 1/65536. Note that the current can never be equal to I unless the number of bits is infinite; in this example 1165536 is the minimum step of current. The value of 1/2 is taken as being the current corresponding to zero signal, so that zero is being represented by 1000000000000000 - current converters cannot deal with negative currents . Maintaining the correct ratios between all of these currents is virtually impossible, though many ingenious techniques have been devised. In particular, this scheme of D-A conversion is very susceptible to a form of crossover distortion, when the zero current level changes to the minimum negative current . In digit form, this is the change from the current 112 (represented by the digital number 1000000000000000) to the lowest negative value which is the sum of all the current from 1/4 down to 1/65536, corresponding to the digital number 01 11111 111111111. This step of current ought to be small, equal to 1/65536, but if any of the more significant current values are incorrect even to the extent of only 0.05%, the effect on this step amount will be devastating - a rise of seven times the minimum current instead of a fall of the minimum step amount, for example . This amount of error is virtually unavoidable, and it will cause a cross-over error to occur each time the signal passes through the zero level, corresponding to a current of 1/2. In addition to this cross-over problem, all converters suffer from 'glitches', which are transient spikes that occur as the bits change. These are caused by small variations in the time when switches open and close, and they also are most serious when the signal level is at its minimum, because they cannot be masked by the signal level, and the number of bits that change is at its greatest when there is a change from zero (1/2 current) to a small negative value . Both of these problems are answered by the adoption of bitstream methods.
Before conversion
The conversion of the digital signal into analog form is just one part of a digital audio receiving system. Before the signal is converted it will have to be error checked and corrected, making use of whatever additional bits have been sent with each number and with each group of numbers . We looked in section 3 at the outline of methods that can be used to detect and correct errors, and in more detail at the simplest method of error correction, the parity bit . The use of a parity bit, though an acceptable method for some systems like serial data communication through wires, is not nearly good enough for digital audio systems, and we have to consider the use of more advanced methods which have been developed from computing. Many of these methods have been known for some time and have featured even in comparatively low-priced 'home' computers of the past as error correction systems for the recording and reproduction of digital signals using ordinary cassette tape. The most important of these systems is called Cyclic Redundancy Checking, or CRC, and a simpler process which is easier to understand is the checksum method, which we shall look at first . The checksum method, as the name suggests, is based on adding the digital numbers over a set . Most digital audio systems work, as we shall see, with a 'frame' that consists of a set of numbers along with synchronizing and error-correcting signals .
Checksum= 4
Alternatively: Sum = 36 = 8 x 4 + 4 remainder

Figure 4.9 The checksum method illustrated with 4-bit numbers . The numbers
are added, ignoring any carry output of the most significant bit, and the
remainder used as the check number which is also transmitted . Repeating this
at the receiver should give a matching checksum. In this example, using 4-bit
numbers means that the carry is for the number 8, so only the difference between
the sum and 8 is carried forward on each addition.
Suppose, for example, that we have 12 numbers in each frame . To make a checksum, we add up the twelve numbers, ignoring any overspill so that the sum will still fit into 16 bits . Figure 4.9 shows an example carried out using four-bit numbers . The checksum number is then recorded as part of the frame . At the receiving end, the numbers are summed in exactly the same way, and compared with the checksum. If there is any disagreement then there has been an error somewhere along the line.
This type of error detection is very much more sensitive than parity, because it is much less likely that a change of 0 to 1 in a number will be balanced by a change from 1 to 0 in exactly the same bit position in another number. The main problem of using a checksum is that it does not indicate where the error is. By using a checksum on a frame, however, we can tell that the error is in that frame or that there is no error in that frame, and this in itself is valuable information. For more precise location of an error, we need some form of checking for each byte or word, and in some applications, the use of a cyclic redundancy check is appropriate.
The basis of CRC is by no means easy to explain if you cannot follow the mathematical analysis that is generally used in text books, but along with an example it can be understood in more concrete terms. The basis of CRC, like so many error detection systems, is the use of extra bits . Suppose, for example, that we have a signal that, for the sake of simplicity, consists of only 5 bits . To code this in a CRC arrangement we might want to use 8 bits, using the extra three bits to act as error detection. The way that this coding is carried out is illustrated in Figure 4.10.
First of all, a 'key' number is selected. This number has to be chosen on the basis of how it will perform, and the selection cannot simply be at random. The size of the key number will be such that it starts with a 1 and makes use of one more bit than we have allowed for error detection. If, for example, we have allowed three bits for error detection, then the key number will use three bits and will start with a 1. The point of this is that if we shift the data number left by three places and then divide it by the key number, the remainder after division will be a number that can be 0 (no remainder) or anything up to three bits of 1’s. For example, if we have allocated 3 bits, and we use 7 as the key number, then the maximum possible remainder is 6, 110 in binary.
Having carried out the division, the remainder is then placed in the lower vacant places of the complete number, which now consists of data bits and remainder bits . Now if this is transmitted without errors, the data part of the number can be tested by dividing it again by the same key. If no errors have occurred, then the same remainder should be obtained. If, however, there has been an error in the transmission of that number then the same remainder will not be obtained. If the key is a suitable one, then altering the data number so that the correct error number is obtained may restore the correct data . This is not foolproof, but works well enough if combined with rejection of any large changes to be a very useful correction system.
-----------------Data: 01101101 (denary 109)
Key: 101 (denary 5)
Remainder of division: 100 (109/5 = 204/5 4 remainder)
Transmitted as: 01101101100
On reception, re-group as 01101101 and 100
01101101 divided by 101 gives 100. Data has no errors.
If data divided by key is not equal to remainder, errors exist.

Figure 4.10 The principle of cyclic redundancy checking requires more bits
to be used. In this example, the 8-bit data number is divided by a 'key' number
of three bits, and the remainder obtained. The data is shifted left by three
places and the remainder added. At the receiver, another check of the same
type should give the same remainder.
The use of cyclic redundancy checking as such can be elaborated, but for digital audio consumer systems, the use of checking on each word takes up too much space and time . A better method is to use a different form of coding, not the simple binary number, and that's a system that we shall look at in Section 6 when we consider the established CD system. First, however, we need to look at two refinements to the system which have arisen since the first CD players started to emerge . Oversampling We saw in Section 2 that sampling creates a set of pulses which are still amplitude modulated and which correspond to the audio signal plus a set of sidebands around the sampling frequency and its harmonics. After the D-A converter has done its work, this is the signal that will exist at the output and as we have seen, it requires low-pass filtering to pass only the audio portion up to 23 kHz and reject the higher frequencies.
This, however, calls for the use of filters with a very stringent specification, and such filters have an effect on the wanted part of the frequency range which is by no means pleasant . A simple way out of the problem would be to double the sampling rate using, for example, 88.2 kHz for a CD system rather than 44 .1 kHz . This is not possible at the recording end of the chain, and since A-D converters are stretched as it is to cope with a rate of 44.1 kHz, it is not possible to double the number of samplings at the A-D converter . What can be done, though, is to add pulses between the output pulses from the A-D converter, Figure 4.11. This creates a pulse stream at 88.2 kHz, and so makes the frequency spectrum quite different, Figure 4. 12. The lowest sideband is now at about 68.2 kHz, well above the 20 kHz limit of the audio signal and easily
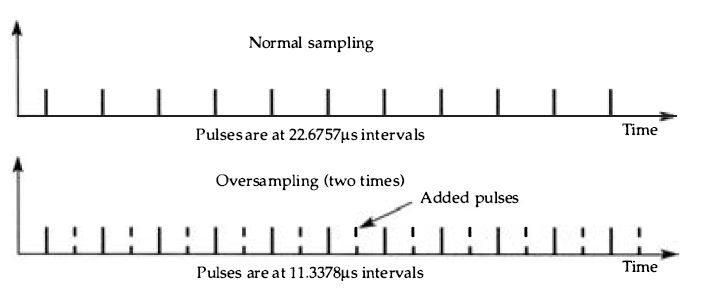
Figure 4.11 Adding pulses that lie between the existing sampled pulses will
halve the time between pulses in the signal, providing a two-times oversampling.
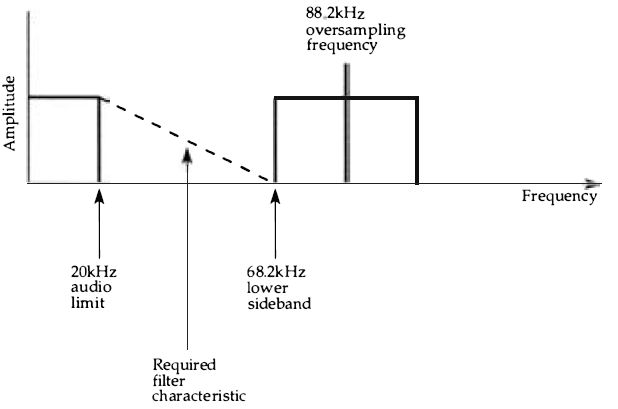
Figure 4.12 The spectrum that arises from two-times oversampling - the gap
between the audio signal and the lower sideband of the oversampling frequency
is much greater, allowing a simpler and more effective filter to be used .
filtered out . In addition, if the added pulses are midway in amplitude between
the original pulses, interpolated values, the conversion from pulses to smoothed
audio can be considerably smoother, just as if the real sampling rate had
been doubled.
Oversampling of four times or even more is now quite common on conventional CD systems, but the whole technology of conventional oversampling D-A conversion has been overturned by the adoption of single-bit (more correctly, single-level) conversion methods, of which bitstream is a well-known example. The combination of oversampling and bitstream is now the conventional system for high-quality CD players . Bitstream methods The most significant development in digital audio in recent years has been the use of bitstream technology. The output of a bitstream converter is not the voltage or current level that is the output of a conventional D-A converter but, as the name suggests, a stream of 0’s and l's in which the ratio of 1's to 0’s represents the ratio of positive to negative in the analog signal . For example, a bitstream of all l's would represent maximum positive voltage, one of all 0' s would represent maximum negative voltage, and one of equal numbers of 1' s and 0' s alternated would represent zero voltage.
The enormous advantages of bitstream conversion are that only one current generator is required, there are no ladder networks needed to accomplish impossibly-precise current division, and the output signal requires no more than a low-pass filter - the bitstream signal is at such a high frequency that a suitable filter is very simple to construct. The disadvantage is that the system must at this point handle very high frequencies - of the order of 11 to 33 MHz for the bitstream converters now being used in CD players . The essence of the bitstream converter is that instead of using a large number of levels at a relatively slow repetition rate, it uses very few levels (2) at a much higher repetition rate. The rate of information processing is the same, but it is accomplished in a very different way.
The principles are surprisingly old, based on a scheme called delta modulation which was developed for long-distance telephone links in the 1940's and 1950's. The normal pulse-code modulation system of sampling and converting the amplitude of the sampled signal into a binary-coded number has well-known drawbacks because of the noise that is generated because of the quantization process . This noise can be forced into higher frequency bands by using higher sampling rates, but since the quantization is fixed at 16-bit at the manufacturing side of CD, nothing can be done to alter the quantization noise that is recorded onto the CD. Other digital systems, however, can use a scheme called delta modulation, in which the difference between samples is converted into binary numbers . If the rate of sampling is very high, the difference is very small, and it can be reduced to one bit only. A signal of this type can be converted back to analog by using an integrator and a low-pass filter. Because of the very severe distortion that occurs when a delta modulator is overloaded, the sigma delta system was developed. This uses sampling of the signal amplitude rather than differences, and forms a stream of pulses by a feedback system, feeding the quantized signal back to be mixed with the incoming samples in an integrator . This results in a noise signal which is not white noise, spread even over the whole range of frequencies, but colored noise, concentrated more at the higher frequencies. Because of this characteristic, this type of modulator is often termed a 'noise-shaper. This is the type of technology, used on other digital systems, which has led to bitstream and other forms of D-A converters in which the number of bits in the signal is reduced.
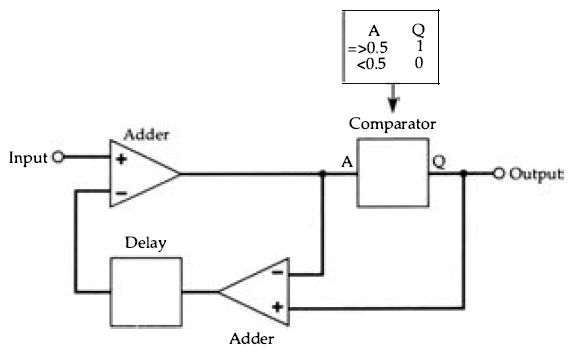
Figure 4.13 A block diagram for a form of noise shaper, using two adders,
a comparator and a delay. The adders are digital adders, and the comparator
has a special truth table shown in the diagram.
Current bitstream converters consist basically of an oversampling stage followed by the circuit called the noise-shaper. The oversampling stage generates pulses at the correct repetition rate, and the noise-shaper uses these pulses to form a stream of 1’s and 0' s at the frequency determined by the oversampling rate. The important part of all this is the action of the noise-shaper.
Figure 4.13 shows the principles of a noise-shaper, which consists of two adders, a converter, and a delay -- the amount of the delay is the time between pulses. If we concentrate on the converter for the moment, this is a circuit which has a very fast response time and which will give an output of 0 for numbers corresponding to less than 0.5 of full output, and an output of 1 for numbers corresponding to more than 0.5 of maximum level.
The generation of the bitstream is done rather like the conversion of a denary number into binary, by successive comparisons giving a 0 or 1 and feeding the remainder of a comparison back to be subtracted from the next (identical) input signal . Note that 0 and 1 from the converter corresponds to 0 or Imax current values in a conventional D-A circuit rather than the digital 0 and 1 of a number.
Imagine a number at the input causing either a 0 or a 1 signal to be developed. The second adder works with one inverted signal, so that its output is the difference between the original signal amplitude number and the maximum signal (output 1) or minimum signal (output 0) . This difference is delayed so that it appears at the input adder while the same oversampled copy of the input is still held there -- the amount of delay will fix how many times this action can be carried out on each input. If the error signal is negative it will be subtracted from the input, otherwise it is added, and the result is fed to the converter. This again will result in a max or min output signal and an error difference, and the error difference is once again fed to the input adder to be added to the new input and so to be converted. At each step, the output is a 1 or a 0 at many times the pulse repetition rate of the oversampled signal, and with the ratio of 0’s and 1's faithfully following the amplitude corresponding to the input numbers.

Figure 4.14 Illustrating how a voltage level in digital terms is reduced
to a set of 0 and I bits to form a bitstream by the action of the noise shaper.
Figure 4.14 illustrates the principle . The input number represents an amplitude of 0.7 and this input will cause the converter to issue an output of 1. The difference is -0.3, and when this is added to the next identical input it gives a net input of 0.4 which causes a 0 output with an error of +0.4. The diagram shows the successive steps which end when the net input to the converter is 1 so that there is no error signal from the output - this ends the conversion which in this example has taken ten steps - implying that the output frequency will be ten times the input frequency.
The output is a stream of 7 1’s and three 0’s, corresponding to a wave that is 70% of full amplitude, an amplitude of 0.7 of maximum.
As might be expected, practice is rather more complicated than this simple example suggests, and some of these complications are noted in Section 6, dealing with the application of bitstream to recent CD players.