|
|
Sigma-Delta A/D Conversion
Traditional successive approximation A/D converters compare the unknown input with accurately known fractions of a reference voltage. Starting with the largest fraction and rejecting any fraction that causes the sum to be larger than the unknown input, k iterations are required for a k-bit word conversion. The input oversampling rates (and conversely, the order of the input filters) are limited by the relatively low speed at which these A/D converters can operate. Hence, analog brick-wall filters are used. Such A/D converters, either directly or through associated circuitry such as brick wall filters, can contribute substantial distortion to the signal.
One way to improve the linearity of conversion is to increase word length. Longer word-length ladder A/D converters were introduced, and these converters improve performance, but resolution is generally constrained to 18 or 20 bits. Thus oversampling A/D converters, using sigma delta architectures, were introduced to remedy the ills of traditional A/D converters and also provide lower cost.
First- and second-order A/D converters provide limited quality, and idle tones can produce audible tones in the noise floor. Attention turned to higher-order (fifth- and sixth order) A/D converters that have reduced idle tones, and reduced sensitivity to clock jitter. Care must be taken to prevent oscillation from modulation overload.
In theory, oversampling A/D conversion is simple: the input signal is first passed through a low-order analog anti aliasing filter, and then sampled at a very high rate to extend the Nyquist frequency. After quantization, the signal passes through a digital filter to prevent aliasing and reduce the sampling frequency to a standard frequency (such as 48 kHz) for storage or processing using normal methods.
In practice, other factors play a role. Only coarse quantization is possible at the highly oversampled rate; this results in a high noise floor. Although noise is spread over a large oversampled spectrum, it is unsatisfactorily high.
Noise shaping must be used to reduce in-band noise. In addition, a conventional digital filter with satisfactory pass band response and stopband attenuation cannot operate at this highly oversampled rate. Rather, a digital decimation filter, operating as a lowpass filter, is used; its computation requirements are far easier. When a sigma-delta quantizer is used, in conjunction with noise shaping, the decimation filter must remove out-of-band quantization noise; this effectively increases the resolution of the digital output.
An analog lowpass filter is required at the converter's input to remove the frequency components that cannot be removed by the digital filter. However, because the preliminary sampling rate is high, the analog lowpass filter is low order. The filter must remove any frequency components outside the audio band to prevent aliasing at the resulting lower sampling rate. This would occur when the output of the digital filter is resampled (undersampled) at the lower downstream sampling rate.
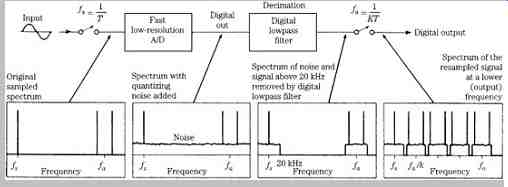
FIG. 16 Diagram showing the theory of oversampling A/D conversion. ( Adams,
1986)
Oversampling A/D converters are unusual in that the basic A/D elements of anti-alias filtering, sampling, and quantization are merged throughout the subsections of the converter. For example, anti-alias filtering occurs in both the input analog filter, and in the digital decimation filter.
Although traditional A/D converters only perform quantization, oversampling A/D converters are complete signal acquisition interfaces.
A diagram illustrating oversampling A/D conversion is shown in FIG. 16. The input signal is first passed through an analog anti-aliasing filter, and the input signal is sampled at a very fast rate (for example, f a= 64 × fs) to extend the Nyquist frequency. The signal is applied to a coarse quantizer such as a sigma-delta converter, which adds (shaped) noise to the signal. The digital data is lowpass-filtered with a cutoff at the Nyquist frequency; this removes out-of-band noise components to prevent anti aliasing. Finally, the signal is resampled at a lower rate (such as 48 kHz) for storage or processing using normal methods. A decimation lowpass filter bandlimits the wideband signal (to 20 kHz in FIG. 16) so that aliasing will not occur when the signal is subsampled at the lower output frequency. A sample-and-hold circuit is not needed because an input sample can be taken during every internal clock cycle. In successive approximation converters, the sampled analog value must be held for the number of clock cycles equal to the number of bits being converted.
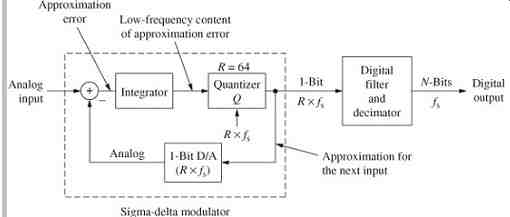
FIG. 17 A first-order sigma-delta modulation circuit showing a one-bit D/A
converter in the feedback loop.
Sigma-Delta A/D Modulator
A sigma-delta modulator can be used to create true one-bit coding from the lowpass-filtered input analog signal. A first order sigma-delta A/D modulator is shown in FIG. 17. In this converter design, the sigma-delta modulator is followed by a digital filter and decimation stage. Because the input sampling rate is high, a simple one-pole RC anti-alias filter suffices. The modulator accepts a sampled analog signal, performs quantizing, and outputs a one-bit signal at a rate determined by the sampling clock. A low-resolution (one-bit quantizer) D/A converter operating at a high sampling rate is placed in a feedback loop. The input to the loop filter is the difference between the input signal and the quantized output converted back to an analog signal; this difference is theoretically equal to the quantization error. The average value of the D/A output (and the modulator output) must approach that of the input signal.
Because a coarse (one-bit A/D) quantizer is used, quantization error at sampling time is large. The coarse output signal is subsequently averaged by the decimation filter, interpolating over several samples (64 or so) to achieve a precise result. High resolution (manifested as dynamic range) is achieved through noise shaping. The integrator can be viewed in the frequency domain as an analog loop filter H(z). The noise-shaping characteristic in this sigma-delta modulator is the inverse of the transfer function of the filter. A filter with higher gain at low frequencies is thus desired to attenuate audio band noise.
This transfer function is essentially a lowpass filter to the signal and a highpass filter to quantization noise; thus, the noise is shifted to a higher frequency. The higher the oversampling rate and order of noise shaping, the higher the resolution of the converter. For example, with an oversampling rate of 64, an ideal second-order modulator yields a signal-to-noise ratio of about 80 dB, equivalent to a 13-bit A/D resolution.
Instead of a one-bit code, converters might produce a multi-bit word of three or four bits using, for example, a sigma-delta modulator modified to contain a multi-bit quantizer. Several quantizer output bits are applied to an internal D/A converter and its analog output is subtracted from the analog input signal, thus producing a quantization error signal. This error signal is applied to the loop filter, and quantized to minimize error and thus yield an output that approximates the input. In this architecture, the dynamic range increases in proportion to the resolution of the quantizer; however, this must be balanced against operating speed. Dynamic range can also be increased by using higher-order filters. Because the output is proportional to the signal's amplitude rather than slope, it is like a PCM converter. Unlike a traditional PCM converter, the noise floor rises with increasing frequency, at 6 dB/octave. Alternatively, a differential pulse code modulator differs from a delta modulator only in that the error signal is quantized to more than one bit. However, such an architecture is still slew-rate limited.
Numerous sigma-delta methods have been applied to A/D conversion, all using a high input sampling rate, and noise shaping. These methods include: single and dual integrator loops, cascaded first-order sigma-delta loops, and multi-bit quantizers with loop filters. The first two methods use true one-bit coders with inherent linearity. The third method uses several bits, and noise is reduced in proportion to the number of quantizer levels used. However, the converter's linearity depends on the linearity of the quantizer. In any case, noise performance hinges on the oversampling rate and order of noise shaping used. Some converter architectures use several first- or second-order sigma-delta coders in combination to achieve higher order, stable noise shaping.
Given a second-order sigma-delta modulator, Charles Thompson has demonstrated that M-bit resolution requires an oversampling rate:
where R is the oversampling rate defined by:
where fa = the oversampling frequency
fs = the output sampling frequency
Thus, 16-bit resolution would require an oversampling rate of 150. A 100-kHz output sampling frequency would necessitate a filter sampling frequency of 15 MHz; this is difficult to achieve. If the order of noise shaping is raised to third-order, the required oversampling rate is described by:
Thus, the required oversampling ratio is 48; this is well within practical design limits.
Depending on its order and design, a sigma-delta feedback loop generally performs the following operations:
subtraction of output from input to find the approximation error, filtering to extract the low-frequency content of the approximation error, sigma-delta D/A conversion of the output code into a signal to subtract it from the input analog signal, and quantization to output an approximation for the next input sample. In practice, a third-order loop can be used to shape the noise toward higher frequencies, where it is removed by the subsequent decimation (undersampling) filter. As with any noise-shaping loop, the signal must be properly dithered to overcome idle tones and other artifacts. In some cases, a dither signal can be applied so that its fundamental and harmonics can be removed by the decimation filter.
Digital Filtering and Decimation
As Robert Adams has pointed out, oversampling converters provide high resolution not by decreasing the error between the analog input and the digital output, but by making the error occur more often. In this way the error spectrum moves beyond the audio passband and although the total noise power is high, the in-band noise power is low. The high bit rate is reduced to more manageable rates through decimation in which a discrete time signal is sampled at a rate lower than the original rate. Decimation provides both an averaging (lowpass) filter and rate reduction. It removes the high-frequency shaped noise, and provides an anti-aliasing function for the final sampling rate.
Looked at in another way, decimation removes the redundant information created by oversampling.
Decimation can be described through a simple example. Sixteen one-bit values could be reduced through a 16:1 decimation to a single multi-bit value; for example, values 1,0,1,0,0,1,0,1,1,0,1,1,1,1,0,0 would be decimated to 9/16, or 0.5625. Because there is only one (multi-bit) output value for every 16 input values, the decimator has decreased the sampling rate by 16:1. As Sangil Park has shown, it is also important to note that decimation has increased resolution; in this example, the input signal is only one bit, but the decimation (averaging) process yields 4-bit resolution (24 = 16) while reducing the sampling rate.
Thus, oversampling followed by decimation demonstrates how speed can be exchanged for resolution. The meaning of the word decimation, incidentally, originally referred to a form of harsh discipline administered by the Roman army to punish cowardice. Soldiers selected for decimation were placed in groups of 10 and drew lots. The soldier on whom the lot fell was executed by his nine comrades, usually by clubbing or stoning.
The decimation process lowpass filters the signal and noise in the one-bit code, band-limiting the code prior to sample-rate reduction to remove alias components.
Decimation also replaces the one-bit coding with 16-bit coding, for example, at a lower sampling rate. However, the computation rate of the filter is not trivial; output samples cannot be discarded (providing decimation) until the filtering computation is complete.
Ideally, the decimation filter would provide a sharp lowpass cutoff at half the output sampling frequency, thus upholding the Nyquist sampling theorem. However, as Robert Adams has shown, this is not always efficient. For example, an FIR filter would require many coefficients because of the high ratio of the input sampling rate to the output sampling rate. Still, when an FIR filter is used, filter outputs are only computed at the lower output sampling rate. An FIR filter is well-suited for decimation. If an IIR filter is used, the feedback loop dictates that an output value must be computed for every input. The decimation function cannot be combined as part of an I IR filter. A practical approach uses two or more stages of decimation, operating at intermediate sampling frequencies. For example, the first stage might use an FIR filter for decimation and a second stage might use an I IR filter for digital filtering. Alternatively, two-stage FIR filters, or two stage I IR filters can be used, with both stages performing some decimation.
If the first stage re-samples at an intermediate frequency fi it would appear that all frequencies above fi/2 must be rejected to prevent subsequent aliasing. However, only certain portions of the spectrum will alias in the audio band, thus the decimation filter need only attenuate those frequency bands. In particular, these alias bands can be identified:
F_alias = I × f1 ± BW Hz
where I = any integer
fi = the decimation filter's intermediate resampling frequency
BW = the audio bandwidth (for example, 20 kHz)
For example, if fi = 96 kHz, the bands of interest will lie at 96, 2 × 96, 3 × 96 kHz, and so on, each occupying a width of 40 kHz. The decimation filter can be designed so that its frequencies of maximum attenuation will coincide with these potentially aliasing frequency bands. A filter with pockets of attenuation, rather than attenuation across the entire stopband, is much easier to implement. As the sampling rate is decreased from one stage to the next, the pockets become proportionally wider and filter complexity increases, but intense computation is performed at the slower rate. In this way, each filter must only reject the signals that would be aliased by the immediate next decimation. Subsequent filters will reject signals that would alias with later decimation. A comb filter is an expedient choice because its design does not require a multiplier (all coefficients are unity).
However, as Sangil Park points out, comb filters cannot wholly remove out-of-band quantization noise so they are followed by additional filter stages of other design. These additional stages can also be needed to compensate for high-frequency drooping caused by the comb filter. A final filter, operating at the slowest sampling rate, could provide a true lowpass characteristic, and correct any frequency response deviations. A comb filter of length R is an FIR filter with coefficients equal to unity; its transfer function is:
In other words, this expression shows a moving average.
For example, if R = 4:
In recursive form, the transfer function can be written as:
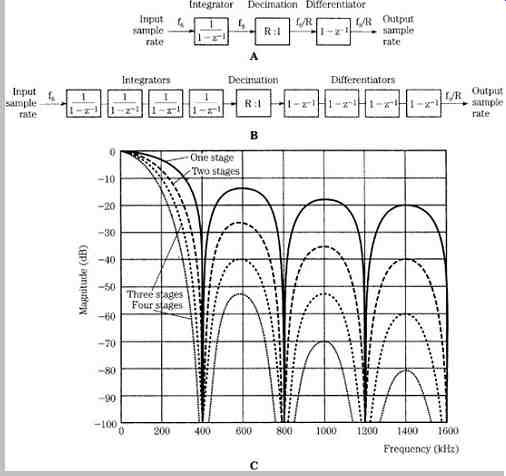
FIG. 18 Comb filters can be used in decimation. A. Block diagram of a one-stage
comb filter. B. Block diagram of a cascaded four-stage comb filter. C. Spectrum
showing the response of one-, two-, three-, and four-stage cascaded comb filter
sections. (Park, 1990b)
This can be expressed in terms of integration followed by differentiation:
This single-stage comb filter decimator can be easily realized, as shown in FIG. 18A. Not only is no storage required for the filter coefficients, but the burden of intermediate computations is decreased owing to the low sampling rate at the differentiator. In addition, the same topology can be used for higher orders of rate change. As noted, in practice, a single comb filter stage does not provide sufficient stopband attenuation to prevent aliasing, thus cascaded stages are often used, as shown in Fig. 18B. In this example, four sections are cascaded, requiring eight data registers and 4(R + 1) additions per input sample. As noted, the comb filter is designed for maximum attenuation at higher frequency components that would alias after rate decimation. FIG. 18C shows the spectrum with one-, two-, three-, and four-stage cascaded comb filter sections.
In some decimator designs, the cascaded comb filter is followed by an FIR filter. The intermediate-rate output from the comb filter is further decimated and the FIR section provides sharp filtering when the sampling frequency is reduced to nominal values (for example, 48 kHz). The decimation factor is typically lower in the FIR section as compared to that in the comb filter section. However, the FIR filter must provide extreme stopband attenuation. In addition, the FIR section can provide compensation for audio band droop caused by the comb filter. FIR computation also provides a linear phase response.
Consider an example in which coding takes place at 64 × 48 kHz = 3.072 MHz. The decimation filter can have two stages. With a 64 × fs Hz input bitstream, the first stage can generate a multi-bit output sample at a sampling frequency of 2 × fs Hz. The second stage of the decimation filter can use a multi-bit multiplier with convolution performed at the output sampling frequency of fs Hz. In all, the decimation filter provides a stopband from 20 kHz to the half-sampling frequency of 1.536 MHz. The analog filter at the system's input is modest, perhaps first- or second-order, ensuring phase linearity in the audio band.
The use of one-bit coding as the intermediate phase of A/D conversion simplifies the filter design. For example, a new output sample is not required for every input bit.
Because the decimation factor is 64 (in this example), an output is required only for every 64 input bits. In practice, the decimation filtering might be carried out in two stages.
An FIR filter would commonly be used for down-sampling, because its non-recursive operation would simplify computation to one sample every 1/fs second. Following decimation, the result can be rounded to 16 bits, and output at a 48-kHz sampling frequency. FIG. 19 summarizes the operation of a sigma-delta A/D converter in the frequency domain.
Digital audio equipment containing A/D (and D/A) converters must have a stable sampling clock that in turn is phase-locked to a distributed master clock. The individual clocks must have very low jitter levels to prevent generated sidebands from rising to audibility. For example, a 16-bit A/D converter might require jitter of less than 20 ps. Jitter is proportionally greater per period for a sigma-delta A/D converter than a ladder converter. Amplitude errors attributable to jitter increase as the input signal frequency increases. However, because the slew rate of the input signal is equal in either type of converter, the amplitude error resulting from sinusoidal jitter is also equal in both cases.
In the case of noise-induced jitter, added noise is distributed over the sigma-delta converter's increased Nyquist frequency range and lowpass-filtered by the decimation circuit. Hence overall in-band jitter-induced noise is less than in some traditional converters. Thus analysis would show that oversampling sigma-delta A/D converters are generally no more sensitive to sinusoidal jitter than a traditional converter and are less susceptible to random noise clock jitter. However, actual performance depends on a converter's specific design. For example, true one-bit converters are generally more susceptible to jitter than multi-bit converters. Timebase correction is discussed in sect. 4.
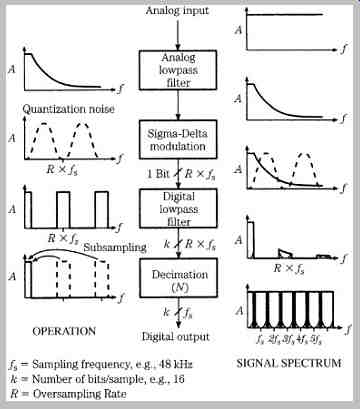
FIG. 19 Summary of spectral characteristics of a one bit A/D converter.
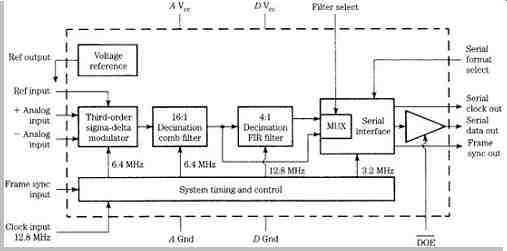
FIG. 20 Internal block diagram of a DSP56ADC16 sigma-delta A/D converter.
(Kloker et al., 1989)
Sigma-Delta A/D Converter Chip
The block diagram of a sigma-delta A/D converter chip is shown in FIG. 20. It is a linear 16-bit converter, using 64 times oversampling, providing output sampling frequencies up to 100 kHz, operating at up to 6.4 MHz. As with other sigma-delta A/D converters, the input signal is oversampled to extend the noise spectrum well beyond the audio band. Noise shaping reduces noise in the audio band, and lowpass-filtering removes out-of-band quantization noise. Finally, the signal is decimated to reduce the sample rate commensurate with the audio band and to increase resolution.
The converter is designed around four major blocks: third-order sigma-delta modulator and noise shaper, 16:1 decimation comb filter, 4:1 decimation FIR filter, and serial interface.
The third-order noise shaper places an 18 dB/octave characteristic on the quantization noise. The analog front end to the converter consists of three differential, switched-capacitor, linear integrators. Filtering and decimation are performed in two steps to reduce the complexity of the digital filter. For example, to achieve the desired stopband attenuation and filter steepness, a single stage FIR with over 2800 taps would be required. Use of a multirate decimation filter system also allows a dual mode application.
The output of the modulator is filtered by a fourth-order comb filter and decimated; the sampling rate is decreased by a factor of 16:1. A comb filter is used because it contains only adders and delay, without need for multiplication. The first stage comb filter accomplishes initial filtering as well as decimation of the input sampling rate by a factor of 16:1. I ts z-domain transfer function can be expressed as:
The equivalent frequency domain transfer function is:
where fs = the filter's sampling frequency.
An FIR filter is used to decimate the signal by a 4:1 factor with a lowpass response. Overall, a 64:1 decimation ratio is achieved. In other words, 63 of every 64 output samples are discarded. A stopband attenuation of -96 dB is achieved. To compensate for the response (passband droop) of the fourth-order comb filter, the FIR uses an inverse equalization response to achieve an overall flat response. FIR images occur at multiples of the comb filter output sampling rate; these are also zeros in the fourth order comb response. The FIR stopband attenuates the comb response, leaving a negligible alias component at the overlap of the two responses. In all, this digital filter section is the equivalent of a 30th-order analog Bessel filter. The output sampling frequency is 100 kHz, with 16-bit resolution and S/N ratio of 90 dB.
Because the cutoff frequencies of the comb and FIR filters are scaled by the input sampling rate, the converter can be used with any arbitrary sampling rate without changing component values. For further flexibility, this A/D converter chip is designed so the 16:1 comb filter can be connected directly to a serial output. This permits operation at faster speed (output sampling frequency of 400 kHz) at the expense of lower resolution (12 bit, and S/N of 72 dB).
This is useful for ultrasonic applications and where lower resolution is tolerable. A general application for this chip using its full resolution is shown in FIG. 21; the A/D converter is connected to a DSP processor.
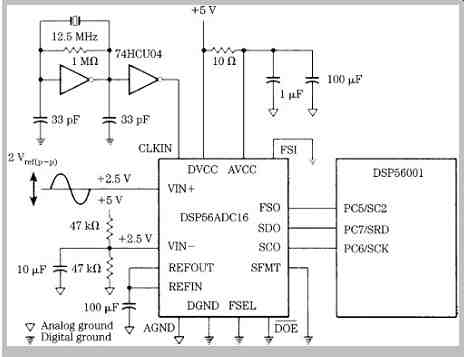
FIG. 21 Application circuit showing an interconnection of a sigma-delta A/D
converter (single-ended mode) and DSP processor.
Sigma-Delta D/A Converter Chip
A typical sigma-delta D/A converter comprises a digital interpolation filter, sigma-delta modulator, and switched capacitor filter. The interpolation filter raises the input sampling frequency to the modulation rate. The modulator reduces the word length to one or a few bits and reduces in-band noise. The switched-capacitor elements filter out of band noise and perform signal D/A reconstruction.
One example of a multi-bit sigma-delta D/A converter uses a second-order mismatch shaping function inside the feedback loop of a high-order modulator. This feature moves element mismatch noise to higher frequencies where it is removed along with other sigma-delta noise by lowpass-filtering. This feature is used in lieu of dynamic element matching (DEM) after the modulator. PCM or DSD data at sample rates up to 200 kHz is input via a serial port and passes through an interpolator and volume control, as shown in FIG. 22. DSD data is volume-adjusted and upsampled by a factor of 2. Data is applied to a sixth-order sigma-delta modulator with integrated second-order mismatch noise shaping. To ensure stability, a fallback second-order sigma-delta modulator can be used. The mismatch noise shaping is not changed when in the fallback mode. When processing SACD data, the modulator also uses a fifth-order Butter-worth lowpass filter with a corner frequency of 50 kHz.
The mismatch shaper effectively provides 16 second order loops with the first and second integrals using 16 elements. The main quantizer outputs the number of elements that the mismatch shaper should turn on. The shaper can override this value to optimize noise shaping.
The number of elements actually turned on is used in the main feedback loop. Even with an element mismatch of 5%, a signal-to-noise ratio of 129 dB is still achieved.
Mismatch shaping can continue for full-scale signals. Some DEM designs can introduce a data-dependent noise floor when given a high-level signal and all elements are turned on. The analog output stage comprises a 16-element switched-capacitor D/A converter operating at 6 MHz.
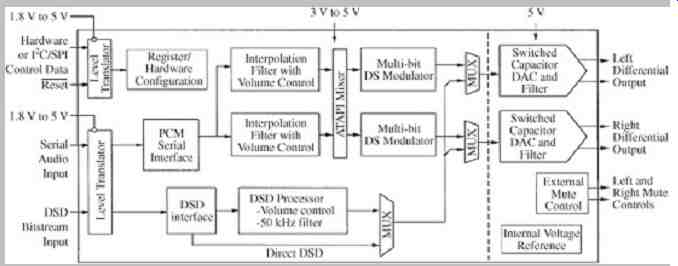
FIG. 22 System architecture of a multi-bit sigma-delta D/A converter with
mismatch shaping in the feedback loop. (Deuw er et al., 2003)
In this design, the noise shaper is inside the main loop; a balance is struck between quantization error and element mismatch error, determined by the number of elements the mismatch shaper turns on. When the quantizer's output is not followed, quantization error increases. The noise contribution from the main loop quantization error, assuming no mismatch, is set equal to the noise from mismatch shaping error, assuming worst case element mismatch.
As with other multi-bit converters, this converter has relatively low quantization noise, low sensitivity to clock jitter, and fewer idle tones compared to many one-bit converters. This design outputs a bitstream compatible with SACD without a decimation filter following the multi-bit conversion. A dynamic range of 120 dB (A-weighted) and distortion level of -105 dB THD+N can be achieved.
Converters such as this are used for CD/SACD/DVD/Blu ray playback.
Sigma-Delta A/D-D/A Converter Chip
Because of the high degree of integration permitted by sigma-delta conversion methods, it is possible to place a linear, 16-bit sigma-delta analog-to-digital and digital-to analog converter on a single chip. One such chip permits input-output sampling frequencies up to 50 kHz with 16-bit resolution, and frequencies of 100 kHz with 12-bit resolution. Third-order noise shaping is used on the A/D side, and fourth-order noise shaping is used on the D/A side. The A/D section uses 64-times oversampling and 64 times decimation. A digital compensation circuit is used to equalize the response to within ±0.025-dB ripple in the passband, with phase linearity.
The D/A section uses two digital anti-imaging interpolation filters, along with an FIR compensation filter for flat passband response. The D/A section provides the output signal. An analog sixth-order Bessel lowpass filter is provided on-chip, as is a temperature-compensated voltage reference for stable coding and clocking. This reference can operate in a master-slave configuration to ensure gain matching and tracking between multiple devices. Likewise, sampling coherency can be preserved between multiple converter chips to ensure interchannel phase accuracy. Digital data can be shifted into and out of the converters with either MSB or LSB first. An SSI bus can be implemented in several different modes.
The DSP56ADA16 provides a dynamic range of 96 dB and signal-to-noise ratio of 90 dB. As with all sigma-delta converters, this converter pair is based on digital filtering techniques, thus approximately 90% of the chip is given to digital circuitry. This promotes compatibility, reliability, increased functionality, and reduced chip cost. Two of these chips form a complete conversion circuit for a stereo signal, and together with a DSP56xxx chip form a complete digital signal processing system.
Noise Shaping of Nonoversampling Quantization Error
As noted, noise shaping is prerequisite in any sigma-delta system to preserve dynamic range when a signal is represented with a reduced number of bits. For example, the noise-shaping characteristic of sigma-delta converters allows one-bit quantization. However, noise shaping can be applied in a variety of ways. For example, a noise-shaping feedback loop can be placed around a quantizer, as shown in FIG. 23. This noise-shaping loop uses the known characteristics of the error generated by the word length reduction (requantization) to alter the spectrum of the requantization noise error.
Recursion places the error information back into the signal, much like negative feedback is used to reduce distortion in analog amplifiers. The quantizer's output error is fed back through a filter and subtracted from the quantizer's input. Because only the difference between the input and output of the quantizer is fed back, the input signal is not affected. The configuration alters the frequency response of the error signal, but not that of the audio signal.
It has the effect of passing the noise through the filter, not the signal.
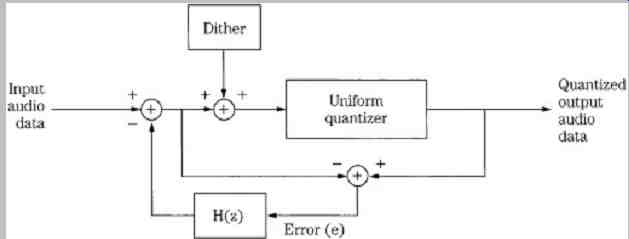
FIG. 23 A requantization topology showing dithering and noise shaping. This
processing reduces quantization distortion artifacts and can be used to reduce
the noise floor in perceptually critical frequency regions.
However, with proper dither, the error is white, and the H(z) filter in the feedback loop spectrally shapes the output error by 1 - H(z). That is, the output error e becomes: [1 - H(z)]e. The noise is shaped by the inverse of the loop transfer function; when a lowpass filter is placed in the loop, the noise spectrum rises with frequency. A filter with high gain at low frequencies yields improved baseband attenuation of noise. Higher-order functions perform a higher-order difference operation on quantizer error, with greater attenuation of baseband noise. The frequency response of the requantization noise can be creatively manipulated by the filter in the feedback loop. For example, the filter's parameters could be dynamically adapted so that the error noise is always optimally masked by the audio signal. The feedback loop must incorporate at least a one-sample z-1 delay; the error cannot be processed until after it has been created by quantization. Theory also dictates that 1 - H(z) must be minimum phase (all poles and zeros within the z-plane unit circle) to preserve the capacity of the channel.
Referring again to FIG. 23, John Vanderkooy and Stanley Lipshitz have pointed out that H(z) represents a loop error that is subtracted from the input at each next sample. This corrects for any such errors on average and gives a highpass shape to both quantization and dither signals present inside the loop. A digital dither signal applied as shown (inside the shaping loop) is identical to a highpass-filtered dither signal applied at a point outside the loop prior to the quantizer. FIG. 24A shows the spectrum of the quantized output of an undithered noise shaper when a 937.5-Hz signal of 1-LSB peak amplitude (approximately -90.3 dBFS) is passed though an undithered requantizer. The spectrum shows many correlated errors with this low-level input signal.

FIG. 24 Dither profoundly affects the spectrum of the signal output from
a noise-shaping circuit. A. Spectrum of a signal with an undithered noise shaper.
B. Spectrum of the signal with a triangular pdf-dithered noise shaper. (Vanderkooy
and Lipshitz, 1989)
When triangular pdf digital dither is applied, a highly uncorrelated spectrum results, as shown in FIG. 24B.
The quantizer and the dither signal noise are both shaped by the loop. A rectangular pdf dither signal could be applied, but could result in noise modulation and limit cycle oscillation. The latter is a repeating output sequence that will produce spectral lines that can yield audible distortion.
Alternatively, a high-pass triangular pdf dither could be applied; requantization noise is shaped as before, but the higher frequency dither signal is shaped to even higher frequencies. However, correlation can result in higher overall noise. In this example, triangular pdf dither with a white spectrum appears to yield the best results.
Psychoacoustically Optimized Noise Shaping
The goal of noise-shaping systems is to dither the audio signal, then shape quantization noise to yield a less audible noise floor. These systems consider the fact that total noise power does not fully describe audibility of noise; perceived loudness also depends on spectral characteristics.
Oversampling noise shapers reduce audio-band quantization noise and increase noise beyond the audio band, where it is inaudible. Nonoversampling noise shapers only redistribute noise energy within the audio band itself. For example, the difference in quantization noise between a 20-bit input signal and a 16-bit output signal can be reshaped to minimize its audibility. In particular, psychoacoustically optimized noise-shaping systems use a feedback filter designed to shape the noise according to an equal-loudness contour or other perceptual weighting function. In addition, such systems can use masking properties to conceal requantization noise.
Sixteen-bit master recordings are not adequate for subsequent music distribution on 16-bit media; for example, for replication of 16-bit CDs. When using a digital console or hard-disk recorder to add equalization, change levels, or perform other digital signal processing, error accumulates in the 16th bit due to computation. It is desirable to use a longer word length, such as 20 bits, that allows processing prior to 16-bit storage. Furthermore, with proper transfer, much information contained in the four LSBs can be conveyed in the upper 16 bits. However, the problem of transferring 20 bits to 16 bits is not trivial.
Simple truncation of the four least-significant bits greatly increases distortion. If the 16th bit is rounded, the improvement is only modest.
It is thus important to re-dither the signal during the requantization that occurs in the transfer. This provides the same benefits as dithering during the original recording. If the most significant bit has not been exercised in the recording, it is possible to bit-shift the entire program upward, thus preserving more of the dynamic range. This is accomplished with a simple gain change in the digital domain. It can be argued that in some cases, for example, when transferring from an analog master tape, a 20-bit interface and noise shaping are not needed because the tape's noise floor makes it self-dithering. However, even then it is important to preserve the analog noise floor which contains useful audio information.
Nonoversampling noise-shaping systems are often used when converting a professional master recording to a consumer format such as a CD. With linear conversion and dither, a 16-bit recording can provide a distortion floor below -110 dBFS. Noise shaping cannot decrease total unweighted noise, but given a 20-bit master recording, subjective performance can be improved by decreasing noise in the critical 1-kHz to 5-kHz region, at the expense of increasing noise in the non-critical 15-kHz region, and increasing total unweighted noise power as well. Because noise shaping removes requantization noise in the most critical region, this noise cannot mask audible details, thus improving subjective resolution. However, the benefit is realized only when output D/A converters exhibit sufficient low-level linearity, and high S/N ratio is available. Indeed, any subsequent requantization must preserve the most critical noise floor improvements, and not introduce other noise that would negate the advantage of a shaped noise floor. For example, 19-bit resolution in D/A converters may be required to fully preserve noise-shaping improvements in a 16-bit recording.
When reducing word length, the audio signal must be redithered for a level appropriate for the receiving medium, for example, 16 bits for CD storage; white triangular pdf dither can be used. A nonoversampling noise-shaping loop redistributes the spectrum of the requantization noise. As noted earlier in this section, sigma-delta noise shapers used in highly oversampled converters yield a contour with a gradually increasing spectral characteristic. This characteristic will not specifically reduce noise in the 1-kHz to 5-kHz region. To take advantage of psychoacoustics, higher-order shapers are used in nonoversampling shapers to form more complicated weighting functions. In this way, the perceptually weighted output noise power is minimized.
A digital filter H(z) in a feedback loop (see FIG. 23) accomplishes this, in which the filter coefficients determine a response so that the output noise is weighted by 1 - H(z), the inverse of the desired psychoacoustic weighting function. The resulting weighted spectrum ideally produces a noise floor that is equally audible at all frequencies.
As Robert Wannamaker suggests, a suitable filter design begins with the selection of a weighting function.
This design curve is inverted, and normalized to yield a zero average spectral power density that represents the squared magnitude of the frequency response of the minimum-phase noise shaper. The desired response is specified, and an inverse Fourier transform is applied to produce an impulse response. The response is windowed to produce a number of filter coefficients corresponding to 1 - H(z), then H(z) is derived from this, yielding an FIR filter.
Theory shows that as very high-order filters H(z) are used to approximate the optimal filter weighting function, the unweighted noise power increases, tending toward infinity with an infinite filter order. For example, although an optimal approximation might yield a 27-dB decrease in audible weighted noise (using a particular weighting curve that reflects the ear's high-frequency roll-off), other weighting functions must be devised, with more modest performance. For example, using a nine-coefficient FIR shaping filter, perceived noise can be decreased by 17 dB compared to unshaped requantization noise. Total unweighted noise power is increased by a reasonable 18 dB compared to an unshaped spectrum. In other words, the output is subjectively as quiet as an unshaped truncated signal with an additional three bits. In this way, audio data with resolution of 19 bits can be successfully transferred to a 16-bit CD. Similar techniques, of course, are applicable to DVD and Blu-ray authoring, when 16-, 20-, or 24-bit words may be used.
Methods that decrease audible noise while increasing total noise (at higher inaudible frequencies) perform a delicate balance. For example, a very high total noise power might damage tweeters, and some listeners suggest that aggressively boosted high-frequency noise produces artifacts, or perhaps masks otherwise audible information.
In practice, depending on the design, the weighting function often approximates a proprietary contour. For example, FIG. 25 shows a proprietary noise-shaping contour, plotted with linear frequency for clarity. In some cases, this curve is fixed; in other cases, the curve is adaptively varied according to signal conditions. Similarly, in some designs, an adaptive dither signal is correlated to the audio signal so the audio signal masks the added dither noise. For example, the audio signal can be spectrally analyzed so that dither frequencies slightly higher in frequency can be generated.
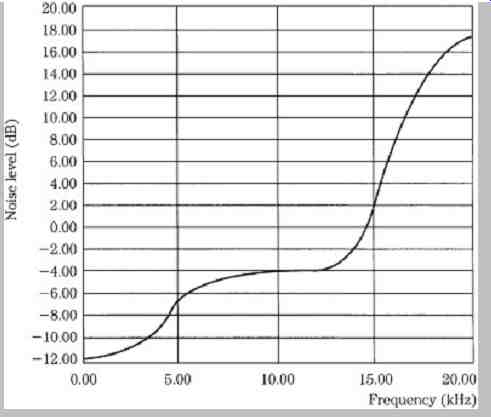
FIG. 25 An equal-loudness noise-shaping curve. This frequency response plot
uses a linear scale to better illustrate the high-frequency contour. (Akune
et al., 1992)
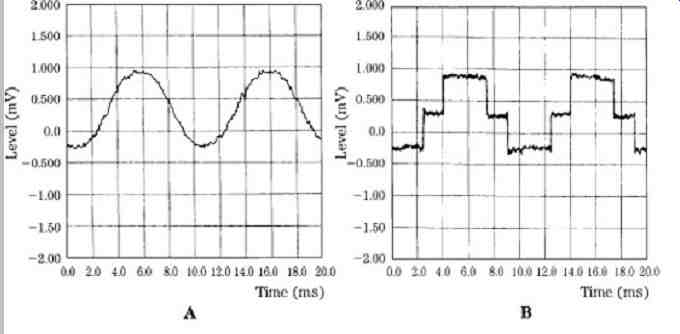
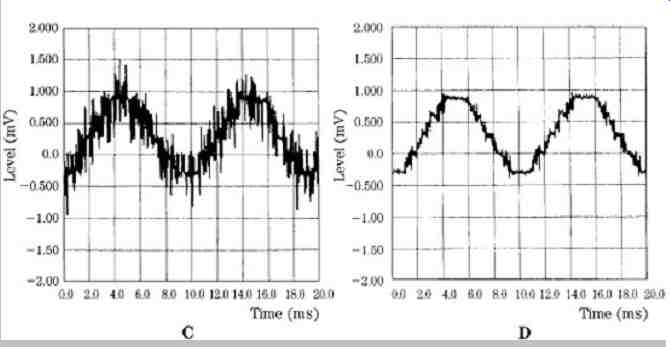
FIG. 26 An example of noise shaping showing a 1 kHz sine wave with -90-dBFS
amplitude. Measurements are made with a 16-kHz lowpass filter. A. Original
20-bit recording. B. Truncated 16-bit signal. C. Dithered 16-bit signal. D.
Noise shaping preserves information in the lower 4 bits.

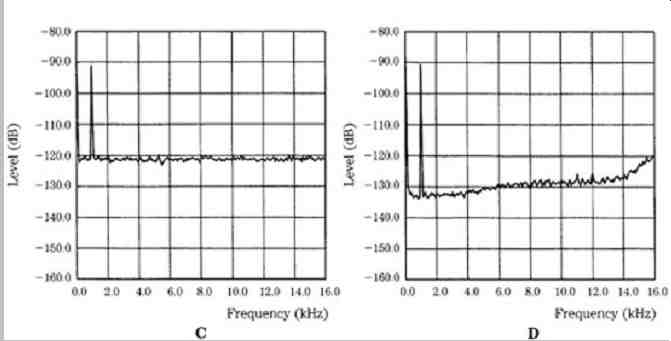
FIG. 27 An example of noise shaping showing the spectrum of a 1 kHz, -90-dBFS
sine wave (from Fig. 26). A. Original 20-bit recording. B. Truncated 16-bit
signal. C. Dithered 16-bit signal. D. Noise shaping reduces low- and mid-frequency
noise, with an increase at higher frequencies.
FIG. 26 shows a 1-kHz sine wave with -90-dBFS amplitude. Measurements are made with a 16-kHz lowpass filter, to approximate the ear's averaging response. A 20 bit recording is quite accurate; when truncated to 16 bits, quantization is clearly evident; when dithered (±1 LSB triangular pdf) to 16 bits, quantization noise is alleviated, but noise is increased; when noise shaping is applied, the noise in this lowpass-filtered measurement is reduced. This 16-bit representation is quite similar to the original 20-bit representation. FIG. 27 shows the spectrum of the same -90-dBFS sine wave, with the four representations.
The 20-bit recording has low error and noise; truncation creates severe quantization error; dithering removes the error but increases noise; noise shaping reduces low- and mid-frequency noise, with an increase at higher frequencies.
In one implementation of a psychoacoustic noise shaper, adaptive error-feedback filters are used to optimize the requantization noise spectrum according to equal-loudness contours as well as masking analysis of the input signal. An algorithm analyzes the signal's masking properties to calculate simultaneous masking curves.
These are adaptively combined with equal-loudness curves to calculate the noise-shaping filter's coefficients, to yield the desired contour. This balance is dynamically and continuously varied according to the power of the input signal. For example, when power is low, masking is minimal, so the equal-loudness contour is used.
Conversely, when power is high, masking is prevalent so the masking contour is more prominently used.
The input signal is converted into critical bands, convolved with critical-band masking curves, and converted to linear frequency to form the masking contour and hence the noise-shaping contour. In other words, masking analysis follows the same processing steps as used in perceptual coding.
Buried Data Technique
With proper dithering and noise shaping, dynamic range can be improved. However, processing can also be applied to use this dynamic range for purposes other than conventional audio headroom. Michael Gerzon and Peter Craven have demonstrated how data can be "buried" in a bitstream. The data is coded with psychoacoustic considerations so the data is inaudible under the masking curve of the audio program; the added data signal is randomized to act as shaped noise. For example, the method could be used to place new information on conventional audio CDs, without significantly degrading the quality of the audio program. In particular, this coding technique replaces several of the least-significant bits of the 16-bit format with independent data. Clearly, if unrelated data simply displaced audio data, and the disc was played in a conventional CD player, the result would be unlistenable. For example, nonstandard data in the four least-significant bits would add about 27 dB of noise to the music, as well as distortion caused by truncating the 16-bit audio signal. The buried data method makes buried data discs compatible with conventional CD players. However, a separate decoder is needed to utilize the buried data.
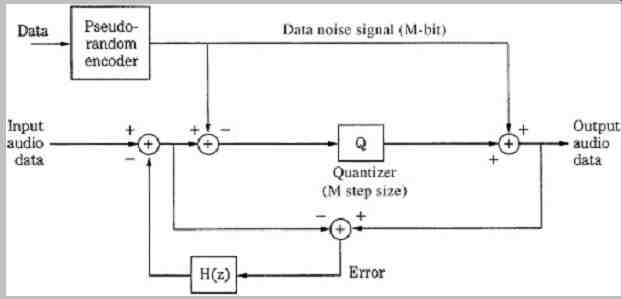
FIG. 28 A buried data channel encoder converts added data to a pseudo-random
noise signal, which is used as a dither signal. This is subtracted from the
audio signal prior to quantization and added to the signal after quantization.
Noise shaping is performed around the quantizer. (Gerzon and Craven, 1995)
An example of the subtractively dithered, noise-shaped quantizer used to encode buried data is shown in Fig. 28. For example, a 16-bit signal is quantized with an M bit step size (rounding the signal to the nearest integer multiple of M) to yield a (16-M)-bit signal. The buried data is coded to be pseudo-random, to make it noise-like with a uniform probability density function. This signal is used as subtractive M-bit dither to remove the artifacts caused by quantization. Specifically, the data dither is subtracted prior to quantization, and then added after quantization, replacing the M least-significant bits of the signal. The quantizing error signal is statistically independent of the input audio signal. To reduce the audibility of the resulting increase in the noise floor, a noise-shaping filter is applied in a loop around the quantizer so that the shaped noise is subtracted from the input signal. The transfer function H(z) is selected so that 1 - H(z) yields a noise floor that ideally lies below the threshold of audibility. Through noise shaping, the noise created by four bits of buried data per channel (conveying 352.8 kbps with stereo channels) can be reduced to yield an overall S/N ratio of about 91 dB, a level that is similar to conventional CDs. Two bits of buried data provide a buried channel rate of 176.4 kbps, while maintaining an S/N ratio of 103 dB.
The average bit rate of the buried data could be increased by variably "stealing" bits from the original program only when their absence will be psychoacoustically masked by the music signal. By using an adaptive noise shaping filter and a variable quantizer step size, the noise shaping characteristic is varied according to the analyzed masking properties of the signal and the noise can be maintained below the masking threshold. The overall buried data rate could exceed 500 kbps, with 800 kbps possible during loud passages, depending on the music program.
Combining methods, for example, buried data might consist of two 2-bit fixed channels, and a variable rate channel; side information would indicate the variable data rate. A buried data CD could be played in a regular CD player; the fidelity of music with limited dynamic range might not be affected at all.
More significantly, a CD player with appropriate decoding (or a player outputting buried data to an external decoder) could play the original music signal, and process buried data as well. The possibilities for buried data are numerous; many audio improvements can be more useful than the lost dynamic range. For example, buried 4-bit data could be used to convey multiple (5.1 channel) audio channels for surround-sound playback; the main left/rights channels are conventionally coded, the buried data carries four additional channels. A hybrid disc would compatibly deliver stereo reproduction with a conventional CD player, and surround sound with a 5.1-channel CD player.
Alternatively, one or two bits of buried data could carry dynamic range compression or expansion information.
Depending on the playback circumstances, the dynamic range of the music could be adjusted for the most desirable characteristics. Because the range algorithms are calculated prior to playback, they are much more effective than conventional real-time dynamic processing. Buried data could convey additional high-frequency information above the Nyquist frequency, and provide a gentle bandlimiting roll-off rate. Any of these applications could be combined, within the limits of the buried data's rate. For example, two ambience channels and dynamic range control data could be delivered simultaneously. Techniques such as these demonstrate the utility of noise shaping and further underscore the power of digital signal processing in digital audio applications.
Links:
Wikipedia: Sigma-Delta modulation