Discrete time sampling is founded on the concept of a rectangular impulse of infinitesimal width. In practice, the width of a rectangular pulse is considered to be of finite width. Although data signals are often characterized by their time-domain properties, the transmission channel is usually best described by its frequency-domain properties. Specifically, it is important to know the bandwidth required for transmission of a sampled signal. The Fourier transform describes a time-domain function in the frequency domain. Given a single rectangular pulse of duration, the transformation of the pulse yields a sin(x)/x function.
This sin(x)/x function is composed of a fundamental cosine wave and its harmonics, its maximum value occurs at x = 0, and it approaches zero as x approaches. The width of the center lobe is exactly at 2/, and the frequency response passes through zero at multiples of 1/.
Importantly, it demonstrates the fundamental nature of sampling as a modulation process; the frequency pattern of the function shows that the rectangular time pulse modulates the amplitude of a carrier frequency. The center frequency can be shifted without altering the shape of the envelope. Clearly, this spectrum extends to infinity; thus, ideal transmission of the pulse would require a system with infinite bandwidth. However, only the central lobe is required; thus, a finite bandwidth will suffice.
Given an understanding of the properties of a single pulse, it is useful to examine a series of such pulses with a periodic repetition of T. This leads to the creation of a practical sampling signal as a periodic series of pulses of fixed amplitude and finite width. The frequency spectrum of this function is defined at discrete values of n; that is, as equally spaced spectral lines with amplitudes corresponding to the discrete frequency components.
Spectral lines are spaced according to the period T. They fall within a | sin(x)/x| envelope that is determined by the pulse duration, duty ratio / T, and pulse amplitude with zero crossings at frequencies that are multiples of 1/.
The spectral response of a series of sampling pulses thus creates spectral lines with amplitudes that follow the same contour as that of a single pulse. The spectrum bandwidth is not affected by the pulse repetition frequency; rather, the bandwidth is determined by the pulse width. The shorter the duration of the pulse, the greater the frequency spread of the bandwidth. It is the case that transmission of narrow pulses requires a channel with a higher bandwidth.
From a frequency-domain standpoint, wider pulses might appear advantageous; however, as viewed in the time domain, narrow pulses permit a greater repetition rate and, for example, permit time multiplexing of channels.
In any case, it is not a higher repetition rate that necessitates a higher bandwidth, but the narrow width of the pulses. Similarly, aperture error can be minimized by decreasing the duration of the pulse width. In the case of ideal sampling with a pulse of infinitesimal width and infinite bandwidth, its spectral lines are placed at multiples of the sampling frequency, as in natural sampling; however, the amplitudes of the lines remain constant across the spectrum.
Given a sampling signal, it is possible to define the sampled signal as the multiplication of the sampling signal, and the message signal. Moreover, we can obtain an expression for the frequency spectrum of the sampled signal. The multiplication of these two time-domain functions can be represented as the convolution of their spectra. The spectrum of the sampled signal contains both positive and negative sidebands centered at the impulses defined by the sampling function, and placed at multiples of the sampling frequency. The spectra are strictly bandlimited. In addition, their amplitude again follows the sin(x)/x contour predicted by the Fourier transform of the sampling signal.
The spectrum of the original message signal is repeated at multiples of the sampling frequency within the envelope of the sampled signal. When proper signal bandlimiting is provided, the spectrum repeats itself without overlap; if the signal's bandwidth is less than the Nyquist (half-sampling) frequency, the image sidebands are separated by a guard band. Note that complete information of the message signal is held in each sideband. The complete signal can be retrieved by removing higher frequency sideband spectra, leaving only the first sideband. As noted, complete information is contained in each sideband, thus, for example, a negative sideband could theoretically be used.
The sin(x)/x function occurs repeatedly in sampling theory and in fact is often called the sampling function.
Given that any practical channel is bandlimited, it is important to know the maximum transmission rate afforded by a channel. Nyquist demonstrated that a message of S Hz can be completely characterized by samples taken at a frequency of 2S Hz. Moreover, the sin(x)/x function can be used as an interpolation function to reconstruct the original signal from the sample values. Each sample is multiplied by its interpolation function, and added to the functions of all other samples to obtain the signal waveform. Importantly, the sin(x)/x function represents the response of an ideal lowpass filter of bandwidth S Hz. In other words, the original signal can be reconstructed exactly by passing the representing samples through a lowpass filter with a bandwidth of S Hz. Thus, as Nyquist stated, a bandlimited signal can be completely reconstructed from samples. This is the key component that permits the transformation of analog signals and digital sequences. The following paragraphs summarize the sampling theorem.
The sampling process defines the values f(nT) of f(t) at regular time intervals. This is equivalent to a multiplication of f(t) and S(t), as shown in Fig. A.1. Therefore:

where (t) is a delta function. The Fourier transform FS() of fS(t) is:
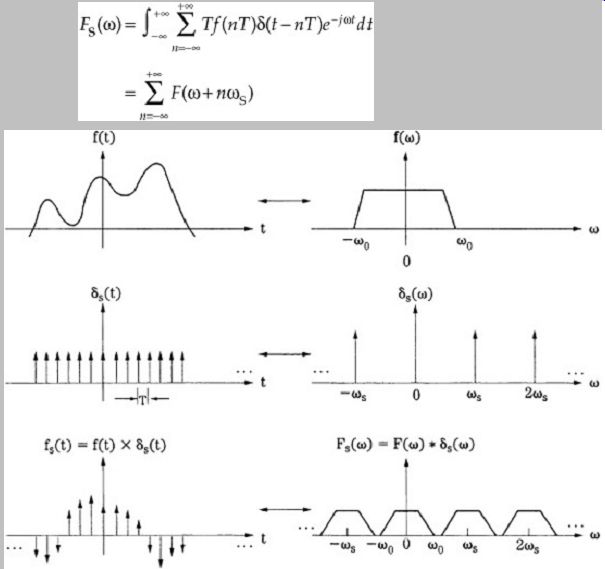
FIG. 1 The sampling process.
... where S = 2/T. When we multiply two functions in time, we are convolving their transforms in the frequency domain.
For this reason, we see the spectrum F() repeated at multiples of the sampling frequency.
We can recover f(t) from FS() by first multiplying it with a gating function G(), as shown in Fig. 2. We have:
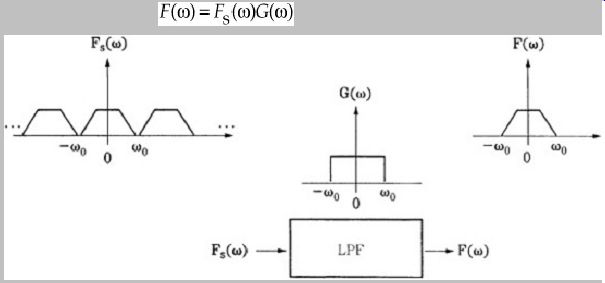
FIG. 2 Recovery of f (t) through lowpass filtering.
That is, we are lowpass filtering FS(). Using the fact that the inverse transform of G() is:
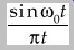
and if FS() fS(t) and G() g(t), then:
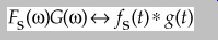
where denotes convolution, and we obtain:
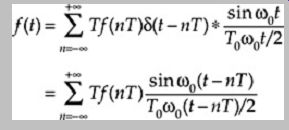
or

This result, known as the sampling theorem, relates the samples f(nT) taken at regular intervals to the function f(t).
The same result can also be interpreted in the following way: f(t) is represented by the Fourier series, which has the sampling function:
sin(x)/x
... as its basis, and each coordinate is weighted by f(nT).
Note that we can only reconstruct the original waveform f(t) from the sampled values if it is bandlimited. In practice, this condition is satisfied by passing f(t) through an anti-aliasing filter.
The quantity:
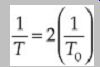
is called the Nyquist rate. This can also be written as fS = 2f0. Hence, the sampling frequency should be twice as high as the maximum input frequency anticipated.